TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
এই নোটবুকটি স্ট্রাকচারাল টাইম সিরিজ (এসটিএস) মডেলগুলির সাথে ফিটিং এবং পূর্বাভাস দেওয়ার সময় একটি (অ-গাউসিয়ান) পর্যবেক্ষণ মডেল অন্তর্ভুক্ত করতে TFP আনুমানিক অনুমান সরঞ্জামগুলির ব্যবহার প্রদর্শন করে। এই উদাহরণে, আমরা পৃথক গণনা ডেটা নিয়ে কাজ করার জন্য একটি পয়সন পর্যবেক্ষণ মডেল ব্যবহার করব।
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
সিন্থেটিক ডেটা
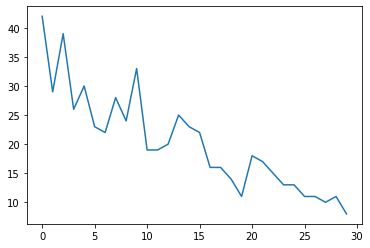
প্রথমে আমরা কিছু সিন্থেটিক গণনা ডেটা তৈরি করব:
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
মডেল
আমরা এলোমেলোভাবে হাঁটার রৈখিক প্রবণতা সহ একটি সাধারণ মডেল নির্দিষ্ট করব:
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
পর্যবেক্ষণ করা সময় সিরিজে কাজ করার পরিবর্তে, এই মডেলটি পয়সন রেট প্যারামিটারের সিরিজে কাজ করবে যা পর্যবেক্ষণগুলিকে নিয়ন্ত্রণ করে।
যেহেতু পয়সন রেট অবশ্যই ইতিবাচক হতে হবে, তাই আমরা প্রকৃত-মূল্যবান STS মডেলটিকে ইতিবাচক মানের উপর একটি বিতরণে রূপান্তর করতে একটি দ্বিজেক্টর ব্যবহার করব। Softplus রূপান্তর \(y = \log(1 + \exp(x))\) যেহেতু এটি প্রায় ইতিবাচক মানের জন্য রৈখিক, একটি প্রাকৃতিক পছন্দ, কিন্তু যেমন অন্য পছন্দ Exp (যা একটি lognormal এলোমেলো হাটা মধ্যে স্বাভাবিক এলোমেলো হাটা রূপান্তরিত) সম্ভব।
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
একটি নন-গাউসিয়ান পর্যবেক্ষণ মডেলের জন্য আনুমানিক অনুমান ব্যবহার করতে, আমরা STS মডেলটিকে একটি TFP জয়েন্ট ডিস্ট্রিবিউশন হিসাবে এনকোড করব। এই যৌথ বন্টনের র্যান্ডম ভেরিয়েবল হল STS মডেলের পরামিতি, সুপ্ত পয়সন হারের টাইম সিরিজ, এবং পর্যবেক্ষিত গণনা।
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
অনুমান জন্য প্রস্তুতি
আমরা পর্যবেক্ষিত গণনা অনুযায়ী, মডেলের অ-পর্যক্ষিত পরিমাণ অনুমান করতে চাই। প্রথমত, আমরা পর্যবেক্ষিত গণনায় জয়েন্ট লগের ঘনত্বকে শর্ত দিই।
pinned_model = model.experimental_pin(observed_counts=observed_counts)
অনুমানটি STS মডেলের প্যারামিটারের সীমাবদ্ধতাগুলিকে সম্মান করে তা নিশ্চিত করার জন্য আমাদের একটি সীমাবদ্ধ বিজেক্টরেরও প্রয়োজন হবে (উদাহরণস্বরূপ, স্কেল অবশ্যই ইতিবাচক হতে হবে)।
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
HMC সঙ্গে অনুমান
আমরা HMC (বিশেষত, NUTS) ব্যবহার করব মডেলের পরামিতি এবং সুপ্ত হারের উপর জয়েন্ট পোস্টেরিয়র থেকে নমুনা নিতে।
এটি HMC-এর সাথে একটি স্ট্যান্ডার্ড STS মডেল ফিট করার চেয়ে উল্লেখযোগ্যভাবে ধীর হবে, যেহেতু মডেলের (অপেক্ষাকৃত কম সংখ্যক) পরামিতিগুলি ছাড়াও আমাদের পয়সন হারের পুরো সিরিজটি অনুমান করতে হবে। তাই আমরা অপেক্ষাকৃত ছোট সংখ্যক পদক্ষেপের জন্য দৌড়াবো; অ্যাপ্লিকেশনের জন্য যেখানে অনুমান গুণমান সমালোচনামূলক হয় এই মানগুলিকে বাড়ানো বা একাধিক চেইন চালানোর জন্য এটি বোধগম্য হতে পারে।
স্যাম্পলার কনফিগারেশন
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
প্রথম আমরা একটি টাঙানো নকশা-বোনা উল্লেখ করুন, এবং তারপর ব্যবহার sample_chain নমুনা উত্পাদন করতে যে স্যাম্পলিং কার্নেল চালানোর জন্য।
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
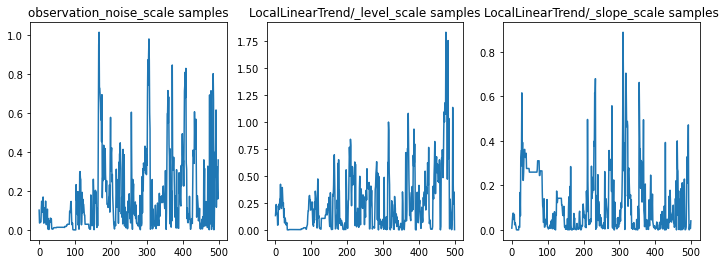
আমরা পরামিতি ট্রেস পরীক্ষা করে অনুমান পরীক্ষা করতে পারি। এই ক্ষেত্রে তারা ডেটার জন্য একাধিক ব্যাখ্যা অন্বেষণ করেছে বলে মনে হচ্ছে, যা ভাল, যদিও আরও নমুনাগুলি চেইনটি কতটা ভালভাবে মিশ্রিত হচ্ছে তা বিচার করতে সহায়ক হবে।
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
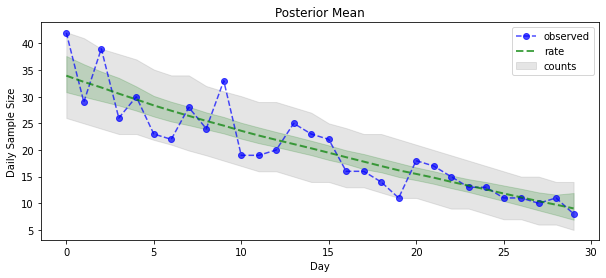
এখন পেঅফের জন্য: আসুন পয়সন হারের পিছনের দিকটি দেখি! আমরা পর্যবেক্ষিত গণনার তুলনায় 80% ভবিষ্যদ্বাণীমূলক ব্যবধানও প্লট করব এবং পরীক্ষা করতে পারি যে এই ব্যবধানটি আমরা বাস্তবে পর্যবেক্ষণ করা গণনার প্রায় 80% ধারণ করেছে।
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
পূর্বাভাস
পর্যবেক্ষিত গণনার পূর্বাভাস দিতে, আমরা সুপ্ত হারের উপর একটি পূর্বাভাস বিতরণ তৈরি করতে স্ট্যান্ডার্ড STS সরঞ্জামগুলি ব্যবহার করব (আবার যেহেতু STS বাস্তব-মূল্যবান ডেটা মডেল করার জন্য ডিজাইন করা হয়েছে), তারপর একটি পয়সন পর্যবেক্ষণের মাধ্যমে নমুনাযুক্ত পূর্বাভাসগুলি পাস করব। মডেল:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
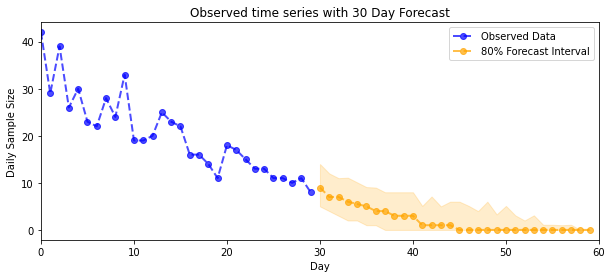
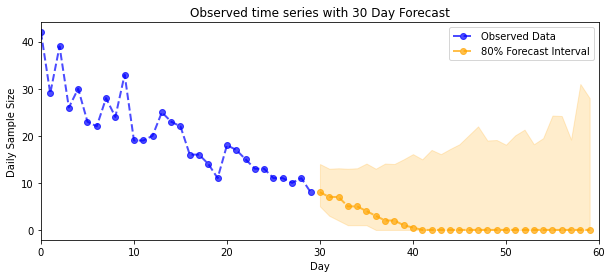
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
VI অনুমান
ভেরিয়েশনাল অনুমান সমস্যাযুক্ত যখন একটি পূর্ণ সময় সিরিজ inferring, আমাদের আনুমানিক গন্য মত (যেমন মান এসটিএস মডেল হিসেবে, একটি সময় সিরিজের মাত্র পরামিতি থেকে ভিন্ন) হতে পারে। মানক অনুমান যে ভেরিয়েবলের স্বাধীন পোস্টেরিয়র আছে তা একেবারেই ভুল, যেহেতু প্রতিটি টাইমস্টেপ তার প্রতিবেশীদের সাথে সম্পর্কযুক্ত, যা অনিশ্চয়তাকে অবমূল্যায়ন করতে পারে। এই কারণে, HMC সম্পূর্ণ সময়ের সিরিজের আনুমানিক অনুমানের জন্য একটি ভাল পছন্দ হতে পারে। যাইহোক, VI বেশ কিছুটা দ্রুত হতে পারে, এবং মডেল প্রোটোটাইপিংয়ের জন্য বা এমন ক্ষেত্রে যেখানে এর কার্যকারিতা পরীক্ষামূলকভাবে 'যথেষ্ট ভাল' হিসাবে দেখানো যেতে পারে সেই ক্ষেত্রে কার্যকর হতে পারে।
আমাদের মডেলকে VI-এর সাথে মানানসই করতে, আমরা কেবল একটি সারোগেট পোস্টেরিয়র তৈরি এবং অপ্টিমাইজ করি:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
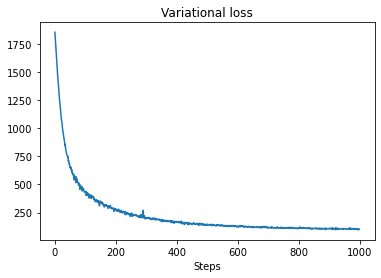
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
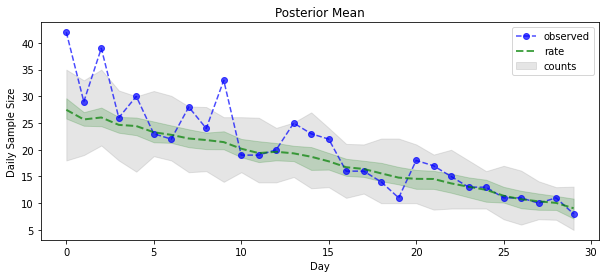
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)