عرض على TensorFlow.org عرض على TensorFlow.org |  تشغيل في Google Colab تشغيل في Google Colab |  عرض المصدر على جيثب عرض المصدر على جيثب |  تحميل دفتر تحميل دفتر |
يوضح هذا الكمبيوتر الدفتري استخدام أدوات الاستدلال التقريبي TFP لتضمين نموذج مراقبة (غير غاوسي) عند تركيب نماذج السلاسل الزمنية الهيكلية (STS) والتنبؤ بها. في هذا المثال ، سنستخدم نموذج مراقبة بواسون للعمل مع بيانات العد المنفصلة.
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
البيانات التركيبية
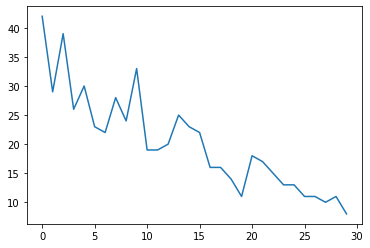
سنقوم أولاً بإنشاء بعض بيانات التعداد التركيبي:
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
نموذج
سنحدد نموذجًا بسيطًا مع اتجاه خطي عشوائي:
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
بدلاً من العمل على السلاسل الزمنية المرصودة ، سيعمل هذا النموذج على سلسلة معلمات معدل بواسون التي تحكم الملاحظات.
نظرًا لأن معدلات Poisson يجب أن تكون موجبة ، فسنستخدم أداة bijector لتحويل نموذج STS ذي القيمة الحقيقية إلى توزيع على القيم الإيجابية. و Softplus التحول \(y = \log(1 + \exp(x))\) هو الاختيار الطبيعي، لأنه ما يقرب من الخطية للقيم إيجابية، ولكن الخيارات الأخرى مثل Exp (والذي يحول المشي العشوائي العادية في المشي العشوائي اللوغاريتمي الطبيعي) من الممكن أيضا.
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
لاستخدام الاستدلال التقريبي لنموذج المراقبة غير الغاوسي ، سنقوم بتشفير نموذج STS باعتباره TFP JointDistribution. المتغيرات العشوائية في هذا التوزيع المشترك هي معلمات نموذج STS ، والسلسلة الزمنية لمعدلات بواسون الكامنة ، والأعداد المرصودة.
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
التحضير للاستدلال
نريد استنتاج الكميات غير المرصودة في النموذج ، بالنظر إلى الأعداد المرصودة. أولاً ، نقوم بشرط كثافة اللوغاريتمات المشتركة على الأعداد المرصودة.
pinned_model = model.experimental_pin(observed_counts=observed_counts)
سنحتاج أيضًا إلى عنصر حيوي مقيد للتأكد من أن الاستدلال يحترم القيود المفروضة على معلمات نموذج STS (على سبيل المثال ، يجب أن تكون المقاييس موجبة).
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
الاستدلال مع HMC
سنستخدم HMC (على وجه التحديد ، NUTS) لأخذ عينات من الجزء الخلفي المشترك عبر معلمات النموذج والمعدلات الكامنة.
سيكون هذا أبطأ بكثير من تركيب نموذج STS قياسي مع HMC ، لأنه بالإضافة إلى معلمات النموذج (عدد صغير نسبيًا) ، يتعين علينا أيضًا استنتاج السلسلة الكاملة لمعدلات بواسون. لذلك سنجري عددًا صغيرًا نسبيًا من الخطوات ؛ بالنسبة للتطبيقات التي تكون فيها جودة الاستدلال أمرًا بالغ الأهمية ، فقد يكون من المنطقي زيادة هذه القيم أو تشغيل سلاسل متعددة.
تكوين العينات
# Allow external control of sampling to reduce test runtimes.
num_results = 500 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 100 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
أولا نحن تحديد العينات، ومن ثم استخدام sample_chain لتشغيل هذا نواة أخذ العينات لعينات المنتجات.
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
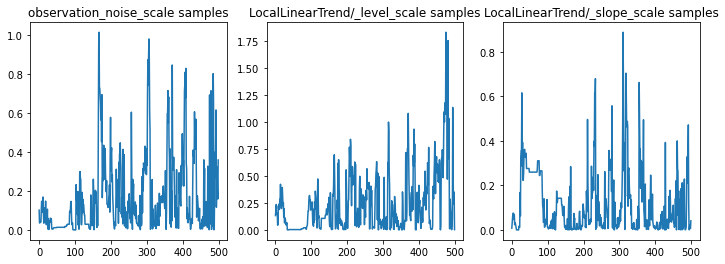
يمكننا التحقق من صحة الاستدلال من خلال فحص آثار المعلمات. في هذه الحالة ، يبدو أنهم اكتشفوا تفسيرات متعددة للبيانات ، وهو أمر جيد ، على الرغم من أن المزيد من العينات سيكون مفيدًا للحكم على مدى جودة خلط السلسلة.
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
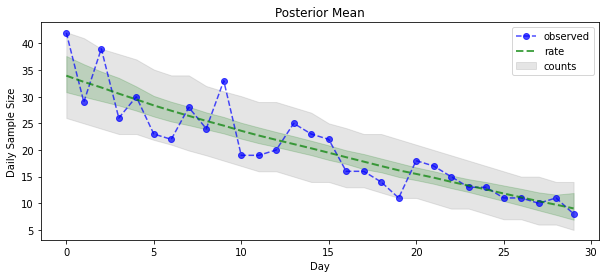
الآن من أجل المكافأة: دعنا نرى اللاحقة على أسعار بواسون! سنقوم أيضًا برسم الفاصل الزمني التنبئي بنسبة 80٪ على التهم المرصودة ، ويمكننا التحقق من أن هذه الفترة تحتوي على حوالي 80٪ من التهم التي لاحظناها بالفعل.
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
التوقع
للتنبؤ بالأعداد التي تمت ملاحظتها ، سنستخدم أدوات STS القياسية لإنشاء توزيع تنبؤي على المعدلات الكامنة (في مساحة غير مقيدة ، مرة أخرى نظرًا لأن STS مصممة لنمذجة البيانات ذات القيمة الحقيقية) ، ثم تمرير تنبؤات العينات من خلال ملاحظة Poisson نموذج:
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
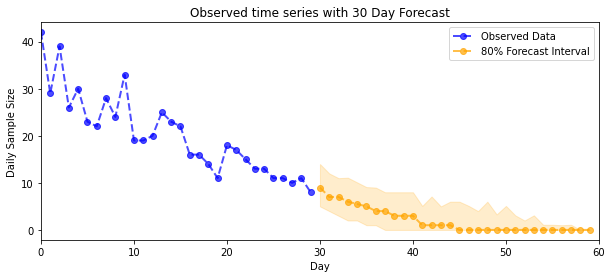
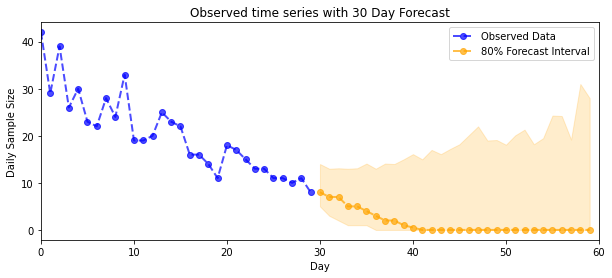
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
السادس الاستدلال
تباين الاستدلال يمكن أن يكون مشكلة عندما استنتاج سلسلة بدوام كامل، مثل تعداد تقريبي لدينا (بدلا من مجرد المعلمات من سلسلة زمنية، كما في نماذج STS القياسية). الافتراض القياسي بأن المتغيرات لها خلفيات مستقلة خاطئة تمامًا ، لأن كل خطوة زمنية مرتبطة بجيرانها ، مما قد يؤدي إلى التقليل من عدم اليقين. لهذا السبب ، قد تكون HMC خيارًا أفضل للاستدلال التقريبي على سلسلة الدوام الكامل. ومع ذلك ، يمكن أن يكون VI أسرع قليلاً ، وقد يكون مفيدًا في النماذج الأولية للنماذج أو في الحالات التي يمكن أن يظهر فيها أداءها تجريبياً على أنه "جيد بما فيه الكفاية".
لتلائم نموذجنا مع VI ، نقوم ببساطة ببناء وتحسين خلفي بديل:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
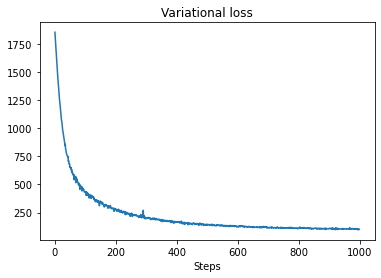
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
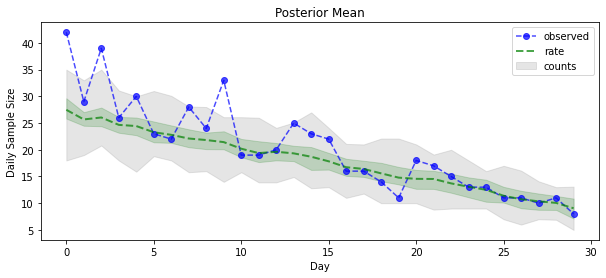
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
plot_forecast_helper(observed_counts, forecast_samples, CI=80)