 TensorFlow.org에서 보기 TensorFlow.org에서 보기 |  Google Colab에서 실행 Google Colab에서 실행 |  GitHub에서 소스 보기 GitHub에서 소스 보기 |  노트북 다운로드 노트북 다운로드 |
확률 주성분 분석 (PCA)이 낮은 차원 공간 잠상을 통해 데이터를 분석하는 차원 축소 기법 ( 팁 주교 1999 ). 데이터에 결측값이 있거나 다차원 척도화에 자주 사용됩니다.
수입품
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
모델
데이터 세트 고려 \(\mathbf{X} = \{\mathbf{x}_n\}\) 의 \(N\) 각 데이터 포인트는, 데이터 포인트, \(D\)차원, $ \ mathbf {X} _n \에서 \ mathbb {R} ^ D\(. We aim to represent each \)\ mathbf {X} _n을 잠재 변수 $ 아래 \(\mathbf{z}_n \in \mathbb{R}^K\) 낮은 치수, $ K <D\(. The set of principal axes \)\ mathbf {W} $ 데이터의 잠재 변수에 관한 것이다.
구체적으로, 우리는 각 잠재 변수가 정규 분포를 따른다고 가정하고,
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
해당 데이터 포인트는 투영을 통해 생성되며,
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
여기서 매트릭스 \(\mathbf{W}\in\mathbb{R}^{D\times K}\) 주축으로 알려져있다. 확률 PCA, 우리는 일반적으로 주축의 추정에 관심이 \(\mathbf{W}\) 및 노이즈 용어\(\sigma^2\).
확률적 PCA는 고전적인 PCA를 일반화합니다. 잠재 변수를 주변화하면 각 데이터 포인트의 분포는 다음과 같습니다.
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
노이즈의 공분산은 무한히 작은 될 때 고전 PCA는 확률 PCA의 특정 케이스입니다 \(\sigma^2 \to 0\).
아래에 모델을 설정했습니다. 우리의 분석에서, 우리는 가정 \(\sigma\) 알려져 있으며, 대신 추정 점의 \(\mathbf{W}\) 모델 매개 변수로, 우리는 주축에 걸쳐 분포를 추론하기 위해 그 위에 이전 놓습니다. 우리는 특히 우리가 사용하는거야하는 총요소 생산성 JointDistribution로 모델을 표현하는 것입니다 JointDistributionCoroutineAutoBatched을 .
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
자료
모델을 사용하여 공동 사전 분포에서 샘플링하여 데이터를 생성할 수 있습니다.
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
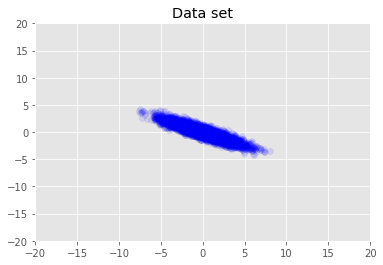
데이터세트를 시각화합니다.
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
최대 사후 추론
먼저 사후 확률 밀도를 최대화하는 잠재 변수의 점 추정치를 검색합니다. 이 같은 최대 사후 (MAP)을 유추 알려져 있으며, 값 계산함으로써 이루어진다 \(\mathbf{W}\) 및 \(\mathbf{Z}\) 후방 밀도 최대화 \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\).
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
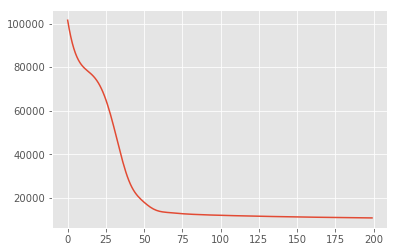
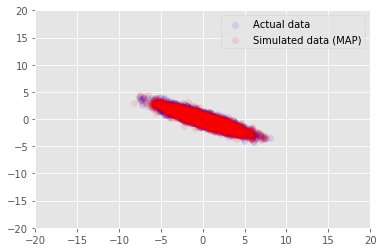
우리의 추정 값에 대한 샘플 데이터 모델을 사용할 수 있습니다 \(\mathbf{W}\) 및 \(\mathbf{Z}\), 우리는 조건으로 실제 데이터 세트에 비교한다.
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
변이 추론
MAP은 사후 분포의 모드(또는 모드 중 하나)를 찾는 데 사용할 수 있지만 이에 대한 다른 통찰력은 제공하지 않습니다. 우리는 옆에 후방 distribtion의 변분 추론, 사용 \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) 변분 분배하여 근사 \(q(\mathbf{W}, \mathbf{Z})\) 에 의해 parametrised \(\boldsymbol{\lambda}\). 목표는 변분 매개 변수를 찾을 수 있습니다 \(\boldsymbol{\lambda}\) 질문과 후방 사이의 KL 발산을 최소화하는 것이 \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\)하한 증거 극대화 동등, 또는, \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\).
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
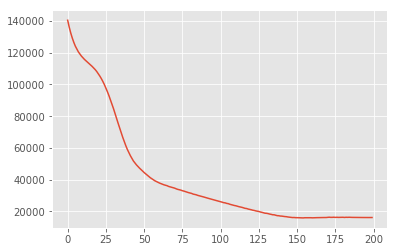
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
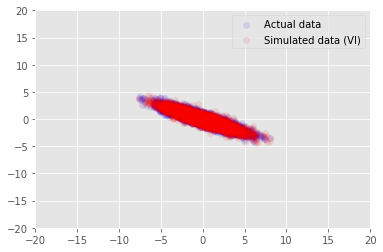
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
감사의 말
이 튜토리얼은 원래 에드워드 1.0 (로 작성된 소스 ). 해당 버전을 작성하고 수정한 모든 기여자에게 감사드립니다.
참고문헌
[1]: 마이클 E. 티핑과 크리스토퍼 M. 비숍. 확률적 주성분 분석. 로얄 통계 학회지 : 시리즈 B (통계 방법론), 61 (3) : 611-622, 1999.
