 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Probabilistik analisis komponen utama (PCA) adalah teknik pengurangan dimensi yang menganalisis data melalui ruang laten dimensi yang lebih rendah ( Tipping dan Uskup 1999 ). Ini sering digunakan ketika ada nilai yang hilang dalam data atau untuk penskalaan multidimensi.
Impor
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Model
Pertimbangkan data set \(\mathbf{X} = \{\mathbf{x}_n\}\) dari \(N\) titik data, dimana setiap titik data adalah \(D\)berdimensi, $ \ mathbf {x} _n \ di \ mathbb {R} ^ D\(. We aim to represent each \)\ mathbf {x} _n $ bawah variabel laten \(\mathbf{z}_n \in \mathbb{R}^K\) dengan dimensi yang lebih rendah, $ K <D\(. The set of principal axes \)\ mathbf {W} $ berkaitan variabel laten untuk data.
Secara khusus, kami mengasumsikan bahwa setiap variabel laten terdistribusi normal,
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
Titik data yang sesuai dihasilkan melalui proyeksi,
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
di mana matriks \(\mathbf{W}\in\mathbb{R}^{D\times K}\) dikenal sebagai sumbu utama. Dalam PCA probabilistik, kita biasanya tertarik dalam memperkirakan sumbu utama \(\mathbf{W}\) dan istilah noise\(\sigma^2\).
PCA probabilistik menggeneralisasi PCA klasik. Meminggirkan variabel laten, distribusi setiap titik data adalah
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
PCA klasik adalah kasus khusus dari PCA probabilistik ketika kovarians dari kebisingan menjadi sangat kecil, \(\sigma^2 \to 0\).
Kami mengatur model kami di bawah ini. Dalam analisis kami, kami menganggap \(\sigma\) diketahui, dan bukan titik memperkirakan \(\mathbf{W}\) sebagai parameter model kita menempatkan sebelum di atasnya dalam rangka untuk menyimpulkan distribusi lebih sumbu utama. Kami akan mengungkapkan model sebagai TFP JointDistribution, khusus, kita akan menggunakan JointDistributionCoroutineAutoBatched .
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
Data
Kita dapat menggunakan model untuk menghasilkan data dengan mengambil sampel dari distribusi prior bersama.
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
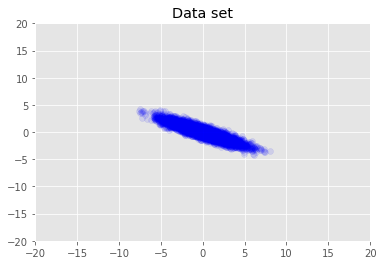
Kami memvisualisasikan kumpulan data.
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
Maksimum Inferensi Posterior
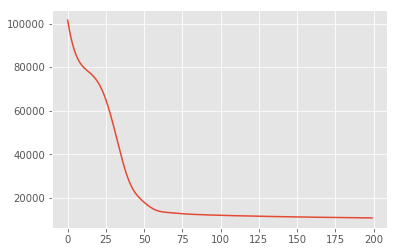
Kami pertama mencari estimasi titik variabel laten yang memaksimalkan kepadatan probabilitas posterior. Hal ini dikenal sebagai maksimum posteriori (MAP) inferensi, dan dilakukan dengan menghitung nilai-nilai \(\mathbf{W}\) dan \(\mathbf{Z}\) yang memaksimalkan posterior density \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\).
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
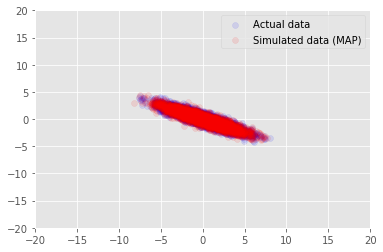
Kita dapat menggunakan model untuk data sampel untuk nilai disimpulkan untuk \(\mathbf{W}\) dan \(\mathbf{Z}\), dan dibandingkan dengan dataset yang sebenarnya kita dikondisikan pada.
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
Inferensi Variasi
MAP dapat digunakan untuk menemukan mode (atau salah satu mode) dari distribusi posterior, tetapi tidak memberikan wawasan lain tentangnya. Kami berikutnya menggunakan inferensi variasional, di mana posterior distribtion \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) didekati menggunakan distribusi variational \(q(\mathbf{W}, \mathbf{Z})\) parametrised oleh \(\boldsymbol{\lambda}\). Tujuannya adalah untuk menemukan parameter variational \(\boldsymbol{\lambda}\) yang meminimalkan perbedaan KL antara q dan posterior, \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\), atau ekuivalen, yang memaksimalkan bukti batas bawah, \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\).
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
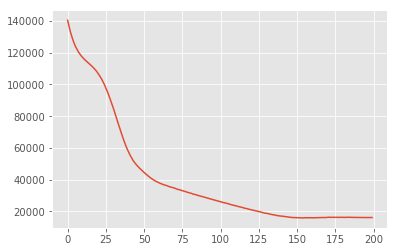
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
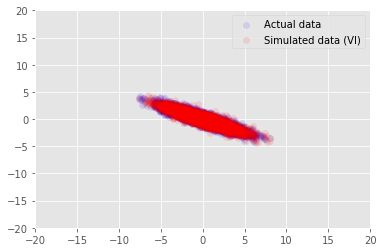
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
ucapan terima kasih
Tutorial ini awalnya ditulis dalam Edward 1.0 ( sumber ). Kami berterima kasih kepada semua kontributor untuk menulis dan merevisi versi itu.
Referensi
[1]: Michael E. Tipping dan Christopher M. Bishop. Analisis komponen utama probabilistik. Jurnal Royal Society Statistik: Seri B (Metodologi statistik), 61 (3): 611-622, 1999.
