 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
संभाव्य प्रमुख घटक विश्लेषण (पीसीए) एक आयामी स्वरूप में कमी तकनीक है कि एक कम आयामी अव्यक्त अंतरिक्ष के माध्यम से डेटा का विश्लेषण करती है ( टिपिंग और बिशप 1999 )। इसका उपयोग अक्सर तब किया जाता है जब डेटा में या बहुआयामी स्केलिंग के लिए लापता मान होते हैं।
आयात
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
आदर्श
किसी डेटा सेट पर विचार करें \(\mathbf{X} = \{\mathbf{x}_n\}\) की \(N\) डेटा बिंदुओं, जहां प्रत्येक डेटा बिंदु है \(D\)आयामी, $ \ mathbf {x} _n \ में \ mathbb {R} ^ डी\(. We aim to represent each \)\ mathbf {x} _n $ एक अव्यक्त चर के तहत \(\mathbf{z}_n \in \mathbb{R}^K\) कम आयाम के साथ, $ कश्मीर <डी\(. The set of principal axes \)\ mathbf {डब्ल्यू} $ आंकड़ों के अव्यक्त चर संबंधित है।
विशेष रूप से, हम मानते हैं कि प्रत्येक गुप्त चर सामान्य रूप से वितरित किया जाता है,
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
संबंधित डेटा बिंदु एक प्रक्षेपण के माध्यम से उत्पन्न होता है,
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
जहां मैट्रिक्स \(\mathbf{W}\in\mathbb{R}^{D\times K}\) प्रिंसिपल कुल्हाड़ियों के रूप में जाना जाता है। संभाव्य पीसीए में, हम आम तौर पर प्रमुख कुल्हाड़ियों का आकलन कर रहे हैं में रुचि रखने वाले \(\mathbf{W}\) और शोर अवधि\(\sigma^2\)।
संभाव्य पीसीए शास्त्रीय पीसीए का सामान्यीकरण करता है। अव्यक्त चर को हाशिए पर रखते हुए, प्रत्येक डेटा बिंदु का वितरण है
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
शास्त्रीय पीसीए संभाव्य पीसीए के विशिष्ट मामला है जब शोर के सहप्रसरण infinitesimally छोटे, हो जाता है \(\sigma^2 \to 0\)।
हमने अपना मॉडल नीचे सेट किया है। हमारे विश्लेषण में, हम यह मान \(\sigma\) जाना जाता है, और अनुमान लगाते समय बिंदु के बजाय \(\mathbf{W}\) एक मॉडल पैरामीटर के रूप में, हम प्रमुख कुल्हाड़ियों पर एक वितरण अनुमान लगाने के लिए में इस पर एक पूर्व जगह। हम एक TFP JointDistribution के रूप में मॉडल को व्यक्त करता हूँ, विशेष रूप से, हम उपयोग करेंगे JointDistributionCoroutineAutoBatched ।
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
आंकड़ा
हम संयुक्त पूर्व वितरण से नमूना लेकर डेटा उत्पन्न करने के लिए मॉडल का उपयोग कर सकते हैं।
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
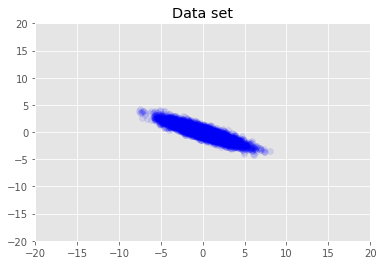
हम डेटासेट की कल्पना करते हैं।
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
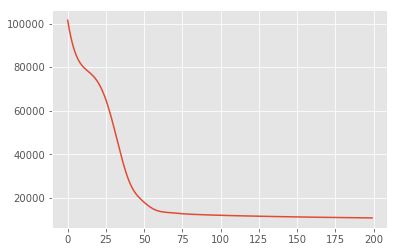
अधिकतम एक पश्चवर्ती अनुमान
हम पहले अव्यक्त चर के बिंदु अनुमान की खोज करते हैं जो पश्च संभाव्यता घनत्व को अधिकतम करता है। यह अधिकतम के रूप में जाना जाता है का अनुमान किया हुआ (एमएपी) अनुमान है, और के मूल्यों की गणना के द्वारा किया जाता है \(\mathbf{W}\) और \(\mathbf{Z}\) कि पीछे घनत्व अधिकतम \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\)।
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
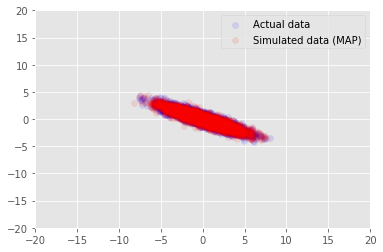
हम लिए लगाए गए अनुमान मूल्यों के लिए नमूना डेटा के लिए मॉडल का उपयोग कर सकते \(\mathbf{W}\) और \(\mathbf{Z}\), और वास्तविक डाटासेट हम पर वातानुकूलित करने के लिए की तुलना करें।
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
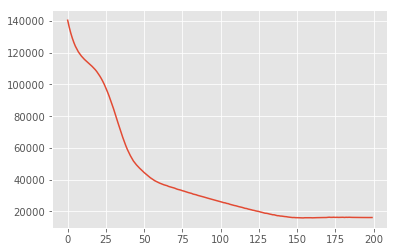
भिन्नात्मक अनुमान
एमएपी का उपयोग पश्च वितरण के मोड (या मोड में से एक) को खोजने के लिए किया जा सकता है, लेकिन इसके बारे में कोई अन्य अंतर्दृष्टि प्रदान नहीं करता है। हम अगले परिवर्तन संबंधी अनुमान है, जहां पीछे distribtion का उपयोग \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) एक परिवर्तन संबंधी वितरण का उपयोग कर अनुमानित किया गया है \(q(\mathbf{W}, \mathbf{Z})\) द्वारा parametrised \(\boldsymbol{\lambda}\)। उद्देश्य परिवर्तन संबंधी मानकों को मिल रहा है \(\boldsymbol{\lambda}\) कि क्ष और पीछे, के बीच केएल विचलन को कम \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\), या समतुल्य है कि सबूत कम ही, अधिकतम \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\)।
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
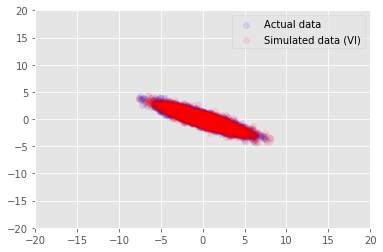
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
स्वीकृतियाँ
इस ट्यूटोरियल मूल रूप से एडवर्ड 1.0 (में लिखा गया था स्रोत )। हम उस संस्करण को लिखने और संशोधित करने के लिए सभी योगदानकर्ताओं को धन्यवाद देते हैं।
संदर्भ
[1]: माइकल ई. टिपिंग और क्रिस्टोफर एम. बिशप। संभाव्य प्रमुख घटक विश्लेषण। रॉयल सांख्यिकीय सोसायटी के जर्नल: श्रृंखला बी (सांख्यिकीय पद्धति), 61 (3): 611-622, 1999।
