PCA הסתברותי

הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

ניתוח מרכיבים העיקרי הסתברותי (PCA) הוא טכניקת הפחתה ממדית שמנתחת נתונים באמצעות מרחב סמוי ממדי נמוך ( Tipping ובישוף 1999 ). הוא משמש לעתים קרובות כאשר חסרים ערכים בנתונים או עבור קנה מידה רב מימדי.

יבוא

import functools
import warnings

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp

from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd

tf.enable_v2_behavior()

plt.style.use("ggplot")
warnings.filterwarnings('ignore')

המודל

קחו ערכת נתונים \(\mathbf{X} = \{\mathbf{x}_n\}\) של \(N\) נקודות נתונים, כאשר כל נקודה הנתונים \(D\)מימדי, mathbf \ $ {x} באסוף נמצאים \ ב \ mathbb {R} ^ D\(. We aim to represent each \)\ mathbf {x} באסוף נמצאים $ תחת משתנה סמוי \(\mathbf{z}_n \in \mathbb{R}^K\) עם ממד נמוך, $ K <D\(. The set of principal axes \)\ mathbf {W} $ מתייחס למשתנים הסמויים לנתונים.

באופן ספציפי, אנו מניחים שכל משתנה סמוי מופץ באופן נורמאלי,

\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]

נקודת הנתונים המתאימה נוצרת באמצעות הקרנה,

\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]

איפה המטריצה \(\mathbf{W}\in\mathbb{R}^{D\times K}\) ידועים כמו צירים עיקריים. בשנת PCA הסתברותית, אנחנו בדרך כלל מעוניינים לאמוד את הצירים העיקריים \(\mathbf{W}\) והרעש לטווח\(\sigma^2\).

PCA הסתברותי מכליל PCA קלאסי. בשוליים החוצה את המשתנה הסמוי, ההתפלגות של כל נקודת נתונים היא

\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]

PCA קלאסית המקרה הספציפי של PCA הסתברותית כאשר השונות המשותפת של הרעש הופך קטן infinitesimally, \(\sigma^2 \to 0\).

הגדרנו את המודל שלנו למטה. בניתוח שלנו, אנו מניחים \(\sigma\) ידוע, ובמקום נקודת מעריך \(\mathbf{W}\) כפרמטר המודל, אנחנו שמים לפני מעליו כדי להסיק חלוקה מעל צירים עיקריים. נצטרך לבטא את המודל בתור הפריון הכולל JointDistribution, במיוחד, נשתמש JointDistributionCoroutineAutoBatched .

def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
  w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
                 scale=2.0 * tf.ones([data_dim, latent_dim]),
                 name="w")
  z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
                 scale=tf.ones([latent_dim, num_datapoints]),
                 name="z")
  x = yield tfd.Normal(loc=tf.matmul(w, z),
                       scale=stddv_datapoints,
                       name="x")

num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5

concrete_ppca_model = functools.partial(probabilistic_pca,
    data_dim=data_dim,
    latent_dim=latent_dim,
    num_datapoints=num_datapoints,
    stddv_datapoints=stddv_datapoints)

model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)

הנתונים

אנו יכולים להשתמש במודל כדי ליצור נתונים על ידי דגימה מההפצה הקודמת המשותפת.

actual_w, actual_z, x_train = model.sample()

print("Principal axes:")
print(actual_w)

Principal axes:
tf.Tensor(
[[ 2.2801023]
 [-1.1619819]], shape=(2, 1), dtype=float32)

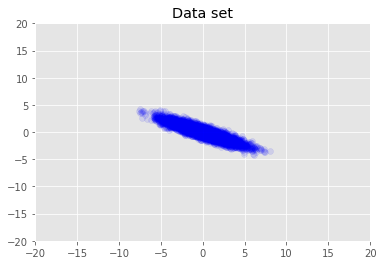
אנו מדמיינים את מערך הנתונים.

plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()

מקסימום מסקנות אחוריות

אנו מחפשים תחילה את אומדן הנקודה של משתנים סמויים שממקסם את צפיפות ההסתברות האחורית. תופעה זו ידועה בשם מקסימלית בדיעבד (MAP) היקש, והוא נעשה על ידי חישוב ערכי \(\mathbf{W}\) ו \(\mathbf{Z}\) כי למקסם את צפיפות האחורי \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\).

w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))

target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
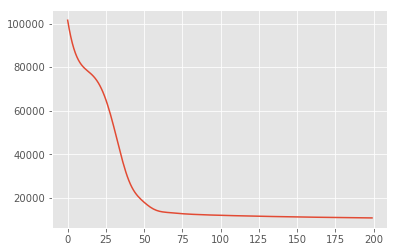
losses = tfp.math.minimize(
    lambda: -target_log_prob_fn(w, z),
    optimizer=tf.optimizers.Adam(learning_rate=0.05),
    num_steps=200)

plt.plot(losses)

[<matplotlib.lines.Line2D at 0x7f19897a42e8>]

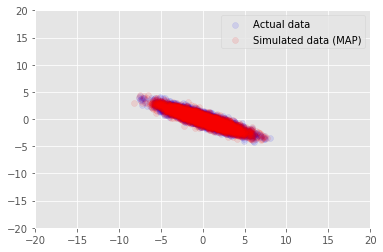
אנחנו יכולים להשתמש במודל נתוני הדגימה עבור בערכים הנגזרים עבור \(\mathbf{W}\) ו \(\mathbf{Z}\), ולהשוות את הנתונים בפועל אנו מותנה.

print("MAP-estimated axes:")
print(w)

_, _, x_generated = model.sample(value=(w, z, None))

plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()

MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
       [-1.4826864]], dtype=float32)>

הסקה וריאציונית

ניתן להשתמש ב-MAP כדי למצוא את המצב (או אחד מהמצבים) של ההתפלגות האחורית, אך אינו מספק שום תובנות אחרות לגביו. אנחנו הבאה להשתמש היקש וריאציה, שבו distribtion האחורי \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) נאמד באמצעות הפצה וריאציה \(q(\mathbf{W}, \mathbf{Z})\) parametrised ידי \(\boldsymbol{\lambda}\). המטרה היא למצוא את הפרמטרים וריאציה \(\boldsymbol{\lambda}\) כי למזער את הבדלי KL בין q ואת האחורי, \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\), או באופן שקול, כי למקסם את הראיות החסם התחתון, \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\).

qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
                                        bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
    1e-4 * tf.ones([latent_dim, num_datapoints]),
    bijector=tfb.Softplus())
def factored_normal_variational_model():
  qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
  qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")

surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
    factored_normal_variational_model)

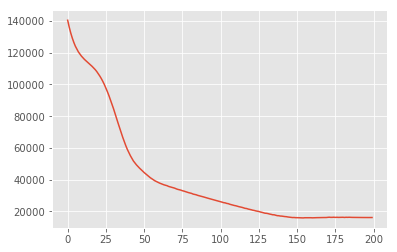
losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn,
    surrogate_posterior=surrogate_posterior,
    optimizer=tf.optimizers.Adam(learning_rate=0.05),
    num_steps=200)

print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)

plt.plot(losses)
plt.show()

Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
       [-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
       [0.00598824]], dtype=float32)>

posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))

# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]

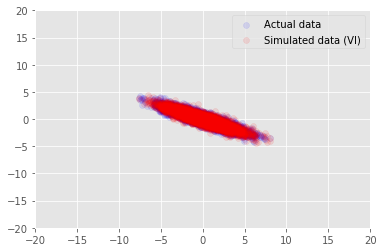
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()

תודות

הדרכה זו נכתבה במקור אדוארד 1.0 ( מקור ). אנו מודים לכל התורמים לכתיבת הגרסה הזו ולתיקון שלה.

הפניות

[1]: מייקל אי. טיפינג וכריסטופר מ. בישופ. ניתוח רכיב עיקרי הסתברותי. כתב העת של האגודה המלכותית סטטיסטי: סדרה B (מתודולוגיה סטטיסטיים), 61 (3): 611-622, 1999.