 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
L' analyse des composantes principales probabilistes (PCA) est une technique de réduction de dimensionnalité qui analyse les données via un espace latent dimensions inférieur ( Tipping et Bishop 1999 ). Il est souvent utilisé lorsqu'il manque des valeurs dans les données ou pour une mise à l'échelle multidimensionnelle.
Importations
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
Le modèle
Soit un ensemble de données \(\mathbf{X} = \{\mathbf{x}_n\}\) de \(N\) points de données, où chaque point de données est \(D\)-dimensionnelle, $ \ mathbf {x} _n \ in \ mathbb {R} ^ D\(. We aim to represent each \)\ mathbf {x} _n $ sous une variable latente \(\mathbf{z}_n \in \mathbb{R}^K\) avec dimension inférieure, $ K <D\(. The set of principal axes \)\ mathbf {W} $ concerne les variables latentes aux données.
Plus précisément, nous supposons que chaque variable latente est normalement distribuée,
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
Le point de données correspondant est généré via une projection,
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
où la matrice \(\mathbf{W}\in\mathbb{R}^{D\times K}\) sont connus comme les axes principaux. Dans PCA probabiliste, nous intéressent généralement à estimer les axes principaux \(\mathbf{W}\) et le terme de bruit\(\sigma^2\).
L'ACP probabiliste généralise l'ACP classique. En marginalisant la variable latente, la distribution de chaque point de données est
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
PCA classique est le cas spécifique de PCA probabiliste lorsque la covariance du bruit devient infinitésimale, \(\sigma^2 \to 0\).
Nous avons mis en place notre modèle ci-dessous. Dans notre analyse, nous supposons \(\sigma\) est connu, et au lieu du point d' estimation \(\mathbf{W}\) comme paramètre de modèle, nous plaçons un avant - dessus afin d' en déduire une distribution sur les axes principaux. Nous exprimons le modèle en tant que TFP JointDistribution, plus précisément, nous allons utiliser JointDistributionCoroutineAutoBatched .
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
Les données
Nous pouvons utiliser le modèle pour générer des données par échantillonnage à partir de la distribution a priori conjointe.
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
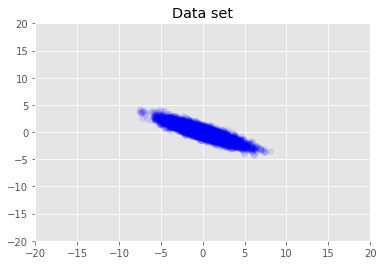
Nous visualisons le jeu de données.
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
Inférence maximale a posteriori
Nous recherchons d'abord l'estimation ponctuelle des variables latentes qui maximise la densité de probabilité postérieure. Ceci est connu comme maximum a posteriori (MAP) inférence, et se fait en calculant les valeurs de \(\mathbf{W}\) et \(\mathbf{Z}\) qui maximisent la densité postérieure \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\).
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
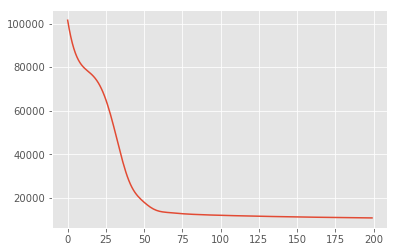
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
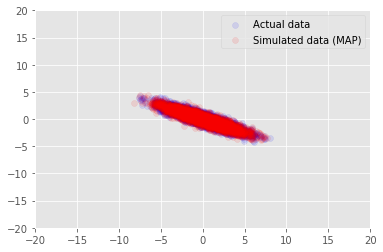
Nous pouvons utiliser le modèle pour exemples de données pour les valeurs inférées pour \(\mathbf{W}\) et \(\mathbf{Z}\)et comparer à l'ensemble de données réelles que nous conditionnés sur.
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
Inférence variationnelle
MAP peut être utilisé pour trouver le mode (ou l'un des modes) de la distribution postérieure, mais ne fournit pas d'autres informations à ce sujet. Nous utilisons ensuite l' inférence variationnelle, où la partie postérieure Distribtion \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) est une distribution estimés à l' aide variationnelle \(q(\mathbf{W}, \mathbf{Z})\) param etr par \(\boldsymbol{\lambda}\). L'objectif est de trouver les paramètres variationnels \(\boldsymbol{\lambda}\) qui minimisent la divergence KL entre q et la partie postérieure, \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\), ou de manière équivalente, qui maximisent la preuve minorant, \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\).
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
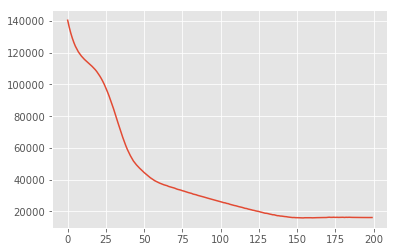
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
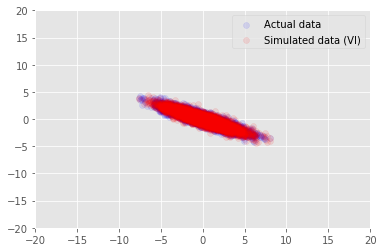
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
Remerciements
Ce tutoriel a été écrit dans Edward 1.0 ( source de ). Nous remercions tous ceux qui ont contribué à la rédaction et à la révision de cette version.
Les références
[1] : Michael E. Tipping et Christopher M. Bishop. Analyse probabiliste en composantes principales. Journal de la Royal Statistical Society: Série B (Méthodologie statistique), 61 (3): 611-622, 1999.
