PCA احتمالی

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

احتمالاتی تحلیل مولفه های اصلی (PCA) یک روش کاهش ابعاد که تجزیه و تحلیل داده ها از طریق یک فضای نهفته پایین بعدی است ( انعام و اسقف 1999 ). اغلب زمانی استفاده می شود که مقادیر گم شده در داده ها یا برای مقیاس بندی چند بعدی وجود داشته باشد.

واردات

import functools
import warnings

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp

from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd

tf.enable_v2_behavior()

plt.style.use("ggplot")
warnings.filterwarnings('ignore')

مدل

در نظر بگیرید یک مجموعه داده \(\mathbf{X} = \{\mathbf{x}_n\}\) از \(N\) نقاط داده ها، که در آن هر داده است \(D\)بعدی، $ میشوند: \ mathbf {X} _N \ در \ mathbb {R} ^ D\(. We aim to represent each \)میشوند: \ mathbf {X} _N $ تحت متغیر مکنون \(\mathbf{z}_n \in \mathbb{R}^K\) با ابعاد کمتر، $ K <D\(. The set of principal axes \)میشوند: \ mathbf {W} $ مربوط به متغیرهای پنهان به داده ها.

به طور خاص، ما فرض می کنیم که هر متغیر پنهان به طور معمول توزیع شده است،

\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]

نقطه داده مربوطه از طریق یک طرح ریزی تولید می شود،

\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]

که در آن ماتریس \(\mathbf{W}\in\mathbb{R}^{D\times K}\) به عنوان محورهای اصلی شناخته شده است. در PCA احتمالی، ما معمولا در برآورد محورهای اصلی علاقه مند \(\mathbf{W}\) و مدت سر و صدا\(\sigma^2\).

PCA احتمالی PCA کلاسیک را تعمیم می دهد. با به حاشیه راندن متغیر پنهان، توزیع هر نقطه داده است

\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]

PCA کلاسیک مورد خاص PCA احتمالاتی است که کوواریانس از سر و صدا بینهایت کوچک، می شود \(\sigma^2 \to 0\).

ما مدل خود را در زیر تنظیم می کنیم. در تحلیل ما، ما فرض \(\sigma\) شناخته شده است، و به جای نقطه برآورد \(\mathbf{W}\) به عنوان یک پارامتر مدل، ما یک قبل بیش از آن به منظور پی بردن به توزیع بیش محورهای اصلی. ما مدل به عنوان یک JointDistribution بهره وری کل عوامل را بیان، به طور خاص، ما استفاده از JointDistributionCoroutineAutoBatched .

def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
  w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
                 scale=2.0 * tf.ones([data_dim, latent_dim]),
                 name="w")
  z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
                 scale=tf.ones([latent_dim, num_datapoints]),
                 name="z")
  x = yield tfd.Normal(loc=tf.matmul(w, z),
                       scale=stddv_datapoints,
                       name="x")

num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5

concrete_ppca_model = functools.partial(probabilistic_pca,
    data_dim=data_dim,
    latent_dim=latent_dim,
    num_datapoints=num_datapoints,
    stddv_datapoints=stddv_datapoints)

model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)

داده

می‌توانیم از مدل برای تولید داده‌ها با نمونه‌گیری از توزیع قبلی مشترک استفاده کنیم.

actual_w, actual_z, x_train = model.sample()

print("Principal axes:")
print(actual_w)

Principal axes:
tf.Tensor(
[[ 2.2801023]
 [-1.1619819]], shape=(2, 1), dtype=float32)

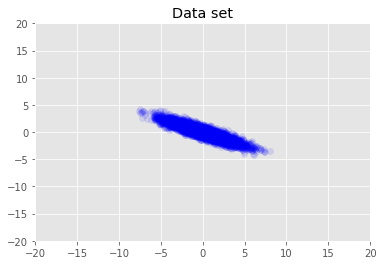
مجموعه داده را تجسم می کنیم.

plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()

حداکثر استنتاج پسینی

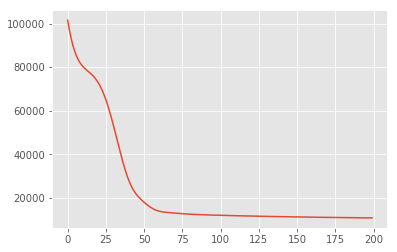
ابتدا تخمین نقطه ای متغیرهای پنهان را جستجو می کنیم که چگالی احتمال خلفی را به حداکثر می رساند. این را به عنوان حداکثر شناخته شده پسینی (MAP) استنتاج، و با محاسبه مقادیر انجام \(\mathbf{W}\) و \(\mathbf{Z}\) که حداکثر رساندن خلفی تراکم \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\).

w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))

target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
losses = tfp.math.minimize(
    lambda: -target_log_prob_fn(w, z),
    optimizer=tf.optimizers.Adam(learning_rate=0.05),
    num_steps=200)

plt.plot(losses)

[<matplotlib.lines.Line2D at 0x7f19897a42e8>]

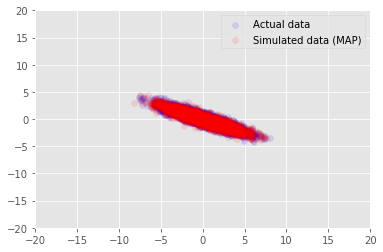
ما می توانیم از این مدل برای داده های نمونه برای ارزش استنباط برای استفاده \(\mathbf{W}\) و \(\mathbf{Z}\)، و نسبت به مجموعه داده واقعی ما در مشروط شده است.

print("MAP-estimated axes:")
print(w)

_, _, x_generated = model.sample(value=(w, z, None))

plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()

MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
       [-1.4826864]], dtype=float32)>

استنتاج متغیر

از MAP می توان برای یافتن حالت (یا یکی از حالت های) توزیع پسین استفاده کرد، اما هیچ بینش دیگری در مورد آن ارائه نمی دهد. ما در کنار استفاده از استنتاج تغییرات، که در آن distribtion خلفی \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) با استفاده از یک توزیع متغیر تقریب است \(q(\mathbf{W}, \mathbf{Z})\) پارامتری شده با \(\boldsymbol{\lambda}\). هدف این است که برای پیدا کردن پارامترهای متغیر \(\boldsymbol{\lambda}\) که به حداقل رساندن اختلاف KL بین q و خلفی، \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\)، یا به طور برابر، که شواهد پایین تر، به حداکثر رساندن \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\).

qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
                                        bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
    1e-4 * tf.ones([latent_dim, num_datapoints]),
    bijector=tfb.Softplus())
def factored_normal_variational_model():
  qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
  qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")

surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
    factored_normal_variational_model)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn,
    surrogate_posterior=surrogate_posterior,
    optimizer=tf.optimizers.Adam(learning_rate=0.05),
    num_steps=200)

print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)

plt.plot(losses)
plt.show()

Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
       [-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
       [0.00598824]], dtype=float32)>

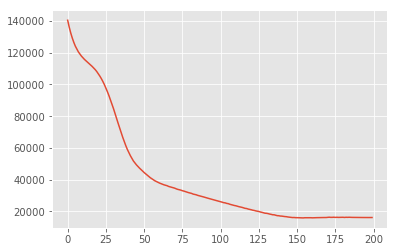
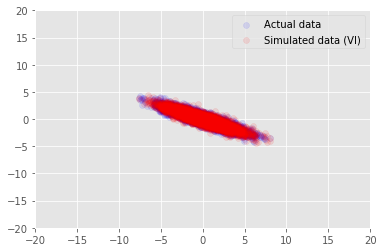
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))

# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]

plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()

سپاسگزاریها

این آموزش در ابتدا در ادوارد 1.0 (نوشته شده بود منبع ). ما از همه مشارکت کنندگان در نوشتن و بازنگری آن نسخه تشکر می کنیم.

منابع

[1]: Michael E. Tipping و Christopher M. Bishop. تحلیل مؤلفه های اصلی احتمالی مجله انجمن سلطنتی آماری: سری B (آماری روش)، 61 (3): 611-622، 1999.