 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
সম্ভাব্য প্রধান উপাদান বিশ্লেষণ (পিসিএ) একটি dimensionality কমানো পন্থা যা একটি নিম্ন মাত্রিক সুপ্ত স্থান মাধ্যমে তথ্য বিশ্লেষণ আছে ( টিপিং এবং বিশপ 1999 )। এটি প্রায়শই ব্যবহৃত হয় যখন ডেটাতে অনুপস্থিত মান থাকে বা বহুমাত্রিক স্কেলিং এর জন্য।
আমদানি
import functools
import warnings
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
মডেলটি
একটি ডেটা সেট বিবেচনা \(\mathbf{X} = \{\mathbf{x}_n\}\) এর \(N\) ডাটা পয়েন্টের, যেখানে প্রতিটি ডেটা বিন্দু \(D\)-dimensional, $ \ mathbf {x এর} _n \ এ \ mathbb {আর} ^ ডি\(. We aim to represent each \)\ mathbf {x এর} _n $ সুপ্ত পরিবর্তনশীল অধীনে \(\mathbf{z}_n \in \mathbb{R}^K\) নিম্ন মাত্রা সঙ্গে, $ কে <ডি\(. The set of principal axes \)\ mathbf {ডব্লিউ} $ ডেটাতে সুপ্ত ভেরিয়েবল সম্পর্কিত।
বিশেষভাবে, আমরা অনুমান করি যে প্রতিটি সুপ্ত পরিবর্তনশীল সাধারণত বিতরণ করা হয়,
\[ \begin{equation*} \mathbf{z}_n \sim N(\mathbf{0}, \mathbf{I}). \end{equation*} \]
সংশ্লিষ্ট ডেটা পয়েন্ট একটি অভিক্ষেপের মাধ্যমে তৈরি করা হয়,
\[ \begin{equation*} \mathbf{x}_n \mid \mathbf{z}_n \sim N(\mathbf{W}\mathbf{z}_n, \sigma^2\mathbf{I}), \end{equation*} \]
যেখানে ম্যাট্রিক্স \(\mathbf{W}\in\mathbb{R}^{D\times K}\) প্রধান অক্ষ বলা হয়। সম্ভাব্য পিসিএ, আমরা সাধারণত প্রধান অক্ষ আনুমানিক হিসাব আগ্রহী \(\mathbf{W}\) এবং গোলমাল মেয়াদ\(\sigma^2\)।
সম্ভাব্য PCA ক্লাসিক্যাল PCA সাধারণীকরণ করে। সুপ্ত ভেরিয়েবলকে প্রান্তিক করে, প্রতিটি ডেটা পয়েন্টের বন্টন
\[ \begin{equation*} \mathbf{x}_n \sim N(\mathbf{0}, \mathbf{W}\mathbf{W}^\top + \sigma^2\mathbf{I}). \end{equation*} \]
ক্লাসিক্যাল পিসিএ সম্ভাব্য পিসিএ নির্দিষ্ট ক্ষেত্রে যখন গোলমাল কোভ্যারিয়েন্স ক্ষুদ্রাতিক্ষুদ্র রূপান্তরিত হবে হয় \(\sigma^2 \to 0\)।
আমরা নীচে আমাদের মডেল সেট আপ. আমাদের বিশ্লেষণ, আমরা অনুমান \(\sigma\) পরিচিত, এবং আনুমানিক হিসাব বিন্দু পরিবর্তে \(\mathbf{W}\) একটি মডেল প্যারামিটার হিসাবে, আমরা অর্ডার প্রধান অক্ষ উপর একটি বিতরণ অনুমান করা এটা উপর একটি পূর্বে রাখুন। আমরা একটি TFP JointDistribution যেমন মডেল প্রকাশ করব, বিশেষভাবে, আমরা ব্যবহার করব JointDistributionCoroutineAutoBatched ।
def probabilistic_pca(data_dim, latent_dim, num_datapoints, stddv_datapoints):
w = yield tfd.Normal(loc=tf.zeros([data_dim, latent_dim]),
scale=2.0 * tf.ones([data_dim, latent_dim]),
name="w")
z = yield tfd.Normal(loc=tf.zeros([latent_dim, num_datapoints]),
scale=tf.ones([latent_dim, num_datapoints]),
name="z")
x = yield tfd.Normal(loc=tf.matmul(w, z),
scale=stddv_datapoints,
name="x")
num_datapoints = 5000
data_dim = 2
latent_dim = 1
stddv_datapoints = 0.5
concrete_ppca_model = functools.partial(probabilistic_pca,
data_dim=data_dim,
latent_dim=latent_dim,
num_datapoints=num_datapoints,
stddv_datapoints=stddv_datapoints)
model = tfd.JointDistributionCoroutineAutoBatched(concrete_ppca_model)
তথ্যটি
আমরা যৌথ পূর্ব বন্টন থেকে নমুনা দ্বারা ডেটা তৈরি করতে মডেলটি ব্যবহার করতে পারি।
actual_w, actual_z, x_train = model.sample()
print("Principal axes:")
print(actual_w)
Principal axes: tf.Tensor( [[ 2.2801023] [-1.1619819]], shape=(2, 1), dtype=float32)
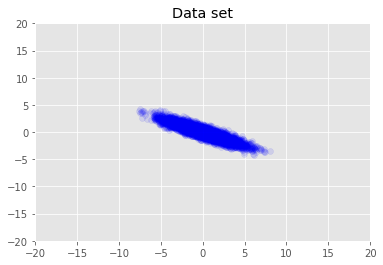
আমরা ডেটাসেট কল্পনা করি।
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1)
plt.axis([-20, 20, -20, 20])
plt.title("Data set")
plt.show()
সর্বাধিক একটি পোস্টেরিওরি অনুমান
আমরা প্রথমে সুপ্ত ভেরিয়েবলের বিন্দু অনুমান অনুসন্ধান করি যা পরবর্তী সম্ভাব্যতা ঘনত্বকে সর্বাধিক করে। এই সর্বোচ্চ হিসাবে পরিচিত হয় আরোহী (MAP) এর ইনফারেন্স এবং মান গণনা করে সম্পন্ন করা হয় \(\mathbf{W}\) এবং \(\mathbf{Z}\) যে অবর ঘনত্ব পূর্ণবিস্তার \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}) \propto p(\mathbf{W}, \mathbf{Z}, \mathbf{X})\)।
w = tf.Variable(tf.random.normal([data_dim, latent_dim]))
z = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
target_log_prob_fn = lambda w, z: model.log_prob((w, z, x_train))
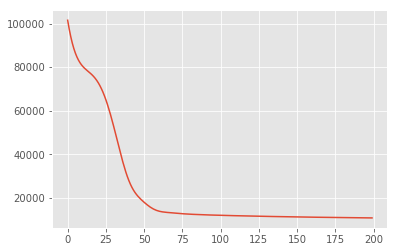
losses = tfp.math.minimize(
lambda: -target_log_prob_fn(w, z),
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f19897a42e8>]
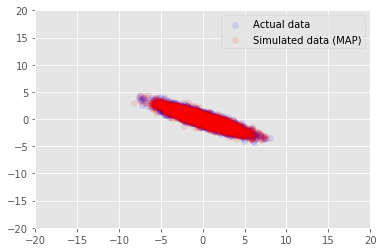
আমরা জন্য আমাদের অনুমিত মানের জন্য নমুনা তথ্য মডেল ব্যবহার করতে পারেন \(\mathbf{W}\) এবং \(\mathbf{Z}\), এবং প্রকৃত ডেটা সেটটি আমরা নিয়ন্ত্রিত করার তুলনা করুন।
print("MAP-estimated axes:")
print(w)
_, _, x_generated = model.sample(value=(w, z, None))
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (MAP)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
MAP-estimated axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.9135954],
[-1.4826864]], dtype=float32)>
পরিবর্তনশীল অনুমান
MAP পোস্টেরিয়র ডিস্ট্রিবিউশনের মোড (বা মোডগুলির একটি) খুঁজে পেতে ব্যবহার করা যেতে পারে, কিন্তু এটি সম্পর্কে অন্য কোন অন্তর্দৃষ্টি প্রদান করে না। আমরা পরের ভেরিয়েশনাল অনুমান, যেখানে অবর distribtion ব্যবহার \(p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X})\) একটি ভেরিয়েশনাল বন্টন ব্যবহার আনুমানিক হয় \(q(\mathbf{W}, \mathbf{Z})\) দ্বারা parametrised \(\boldsymbol{\lambda}\)। লক্ষ্য ভেরিয়েশনাল পরামিতি খুঁজে পেতে \(\boldsymbol{\lambda}\) যে কুই এবং অবর মধ্যে কেএল বিকিরণ কমান \(\mathrm{KL}(q(\mathbf{W}, \mathbf{Z}) \mid\mid p(\mathbf{W}, \mathbf{Z} \mid \mathbf{X}))\), অথবা equivalently, যে প্রমাণ লোয়ার বাউন্ড পূর্ণবিস্তার \(\mathbb{E}_{q(\mathbf{W},\mathbf{Z};\boldsymbol{\lambda})}\left[ \log p(\mathbf{W},\mathbf{Z},\mathbf{X}) - \log q(\mathbf{W},\mathbf{Z}; \boldsymbol{\lambda}) \right]\)।
qw_mean = tf.Variable(tf.random.normal([data_dim, latent_dim]))
qz_mean = tf.Variable(tf.random.normal([latent_dim, num_datapoints]))
qw_stddv = tfp.util.TransformedVariable(1e-4 * tf.ones([data_dim, latent_dim]),
bijector=tfb.Softplus())
qz_stddv = tfp.util.TransformedVariable(
1e-4 * tf.ones([latent_dim, num_datapoints]),
bijector=tfb.Softplus())
def factored_normal_variational_model():
qw = yield tfd.Normal(loc=qw_mean, scale=qw_stddv, name="qw")
qz = yield tfd.Normal(loc=qz_mean, scale=qz_stddv, name="qz")
surrogate_posterior = tfd.JointDistributionCoroutineAutoBatched(
factored_normal_variational_model)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior=surrogate_posterior,
optimizer=tf.optimizers.Adam(learning_rate=0.05),
num_steps=200)
print("Inferred axes:")
print(qw_mean)
print("Standard Deviation:")
print(qw_stddv)
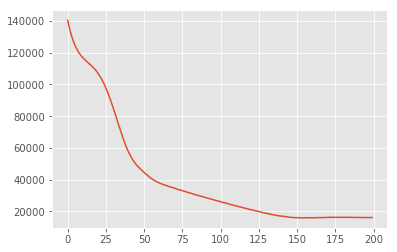
plt.plot(losses)
plt.show()
Inferred axes:
<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[ 2.4168603],
[-1.2236133]], dtype=float32)>
Standard Deviation:
<TransformedVariable: dtype=float32, shape=[2, 1], fn="softplus", numpy=
array([[0.0042499 ],
[0.00598824]], dtype=float32)>
posterior_samples = surrogate_posterior.sample(50)
_, _, x_generated = model.sample(value=(posterior_samples))
# It's a pain to plot all 5000 points for each of our 50 posterior samples, so
# let's subsample to get the gist of the distribution.
x_generated = tf.reshape(tf.transpose(x_generated, [1, 0, 2]), (2, -1))[:, ::47]
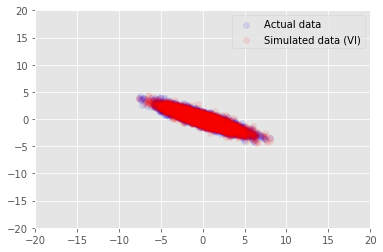
plt.scatter(x_train[0, :], x_train[1, :], color='blue', alpha=0.1, label='Actual data')
plt.scatter(x_generated[0, :], x_generated[1, :], color='red', alpha=0.1, label='Simulated data (VI)')
plt.legend()
plt.axis([-20, 20, -20, 20])
plt.show()
স্বীকৃতি
এই টিউটোরিয়ালটি মূলত এডওয়ার্ড 1.0 (লেখা ছিল উৎস )। আমরা সেই সংস্করণটি লেখা এবং সংশোধন করার জন্য সমস্ত অবদানকারীদের ধন্যবাদ জানাই।
তথ্যসূত্র
[১]: মাইকেল ই. টিপিং এবং ক্রিস্টোফার এম. বিশপ। সম্ভাব্য প্রধান উপাদান বিশ্লেষণ। রয়েল পরিসংখ্যানগত সোসাইটির জার্নাল: সিরিজ বি (পরিসংখ্যানগত পদ্ধতি), 61 (3): 611-622, 1999।
