การเลือกรุ่นเบย์เซียน
 ดูบน TensorFlow.org ดูบน TensorFlow.org |  ทำงานใน Google Colab ทำงานใน Google Colab |  ดูแหล่งที่มาบน GitHub ดูแหล่งที่มาบน GitHub |  ดาวน์โหลดโน๊ตบุ๊ค ดาวน์โหลดโน๊ตบุ๊ค |
นำเข้า
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
งาน: การตรวจจับจุดเปลี่ยนด้วยจุดเปลี่ยนหลายจุด
พิจารณางานการตรวจจับจุดเปลี่ยน: เหตุการณ์เกิดขึ้นในอัตราที่เปลี่ยนแปลงตามเวลา ขับเคลื่อนโดยการเปลี่ยนแปลงอย่างกะทันหันในสถานะ (ไม่ได้สังเกต) ของระบบบางระบบหรือกระบวนการสร้างข้อมูล
ตัวอย่างเช่น เราอาจสังเกตชุดของการนับดังต่อไปนี้:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
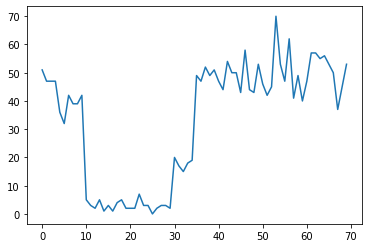
สิ่งเหล่านี้อาจแสดงถึงจำนวนความล้มเหลวในดาต้าเซ็นเตอร์ จำนวนผู้เข้าชมหน้าเว็บ จำนวนแพ็กเก็ตบนลิงก์เครือข่าย ฯลฯ
โปรดทราบว่ายังไม่ชัดเจนว่าระบอบการปกครองของระบบที่แตกต่างกันมีมากเพียงใดจากการดูข้อมูล คุณบอกได้ไหมว่าจุดสวิตช์ทั้งสามจุดเกิดขึ้นที่ใด
จำนวนรัฐที่ทราบ
ก่อนอื่นเราจะพิจารณากรณี (อาจไม่สมจริง) ซึ่งทราบจำนวนสถานะที่ไม่ได้สังเกตมาก่อน ในที่นี้ เราจะถือว่าเรารู้ว่ามีสถานะแฝงอยู่สี่สถานะ
เราจำลองปัญหานี้เป็นสลับ (inhomogeneous) กระบวนการ Poisson: ที่จุดในแต่ละครั้งจำนวนของเหตุการณ์ที่เกิดขึ้นเป็น Poisson กระจายและอัตราของเหตุการณ์ที่เกิดขึ้นจะถูกกำหนดโดยไม่มีใครสังเกตสถานะของระบบ \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
แฝงรัฐมีความไม่ต่อเนื่อง: \(z_t \in \{1, 2, 3, 4\}\)ดังนั้น \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) เป็นเวกเตอร์ที่เรียบง่ายที่มีอัตรา Poisson แต่ละรัฐ การจำลองการวิวัฒนาการของรัฐในช่วงเวลาที่เราจะกำหนดง่ายการเปลี่ยนแปลงรูปแบบการ \(p(z_t | z_{t-1})\): ขอบอกว่าในแต่ละขั้นตอนเราอยู่ในสถานะที่ก่อนหน้านี้มีบางอย่างที่น่าจะเป็น \(p\)และมีความน่าจะเป็น \(1-p\) การเปลี่ยนแปลงที่เราไป รัฐต่าง ๆ อย่างสม่ำเสมอโดยสุ่ม สถานะเริ่มต้นยังถูกสุ่มเลือกอย่างสม่ำเสมอ ดังนั้นเราจึงมี:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
สมมติฐานเหล่านี้สอดคล้องกับ รูปแบบมาร์คอฟที่ซ่อนอยู่ กับการปล่อย Poisson เราสามารถเข้ารหัสไว้ใน TFP ใช้ tfd.HiddenMarkovModel ขั้นแรก เรากำหนดเมทริกซ์การเปลี่ยนแปลงและชุดเครื่องแบบก่อนในสถานะเริ่มต้น:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
ต่อไปเราจะสร้าง tfd.HiddenMarkovModel กระจายใช้ตัวแปรสุวินัยเพื่อเป็นตัวแทนของอัตราที่เกี่ยวข้องกับแต่ละสถานะของระบบ เรากำหนดพารามิเตอร์อัตราในพื้นที่บันทึกเพื่อให้แน่ใจว่ามีค่าเป็นบวก
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
สุดท้ายเรากำหนดความหนาแน่นบันทึกรูปแบบของทั้งหมดรวมทั้ง lognormal ไม่ค่อยให้ข้อมูลก่อนที่อัตราและเรียกใช้เพิ่มประสิทธิภาพการคำนวณ สูงสุด posteriori (MAP) พอดีกับข้อมูลนับสังเกต
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
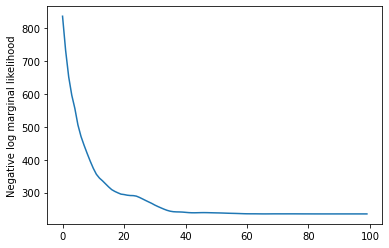
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
มันได้ผล! โปรดทราบว่าสถานะแฝงในแบบจำลองนี้สามารถระบุได้จนถึงการเปลี่ยนแปลงเท่านั้น ดังนั้นอัตราที่เรากู้คืนจึงอยู่ในลำดับที่ต่างออกไป และมีสัญญาณรบกวนเล็กน้อย แต่โดยทั่วไปแล้วจะเข้ากันได้ดี
ฟื้นฟูวิถีของรัฐ
ตอนนี้เราได้เหมาะสมกับรูปแบบที่เราอาจต้องการที่จะสร้างรัฐซึ่งรูปแบบเชื่อว่าระบบได้ในแต่ละ timestep
นี้เป็นงานการอนุมานหลัง: ที่กำหนดนับสังเกต \(x_{1:T}\) และพารามิเตอร์แบบ (อัตราค่าบริการ) \(\lambda\)เราต้องการที่จะอนุมานลำดับของตัวแปรแฝงที่ไม่ต่อเนื่องตามการกระจายหลัง \(p(z_{1:T} | x_{1:T}, \lambda)\)ในโมเดล Markov ที่ซ่อนอยู่ เราสามารถคำนวณส่วนเพิ่มและคุณสมบัติอื่นๆ ของการกระจายนี้ได้อย่างมีประสิทธิภาพโดยใช้อัลกอริธึมการส่งข้อความมาตรฐาน โดยเฉพาะอย่างยิ่ง posterior_marginals วิธีการได้อย่างมีประสิทธิภาพจะคำนวณ (โดยใช้ อัลกอริทึมไปข้างหน้าย้อนกลับ ) ร่อแร่กระจาย \(p(Z_t = z_t | x_{1:T})\) เหนือรัฐไม่ต่อเนื่องแฝง \(Z_t\) ในแต่ละ timestep \(t\)
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
การพล็อตความน่าจะเป็นหลัง เรากู้คืน "คำอธิบาย" ของแบบจำลองของข้อมูล: แต่ละสถานะทำงาน ณ จุดใด
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
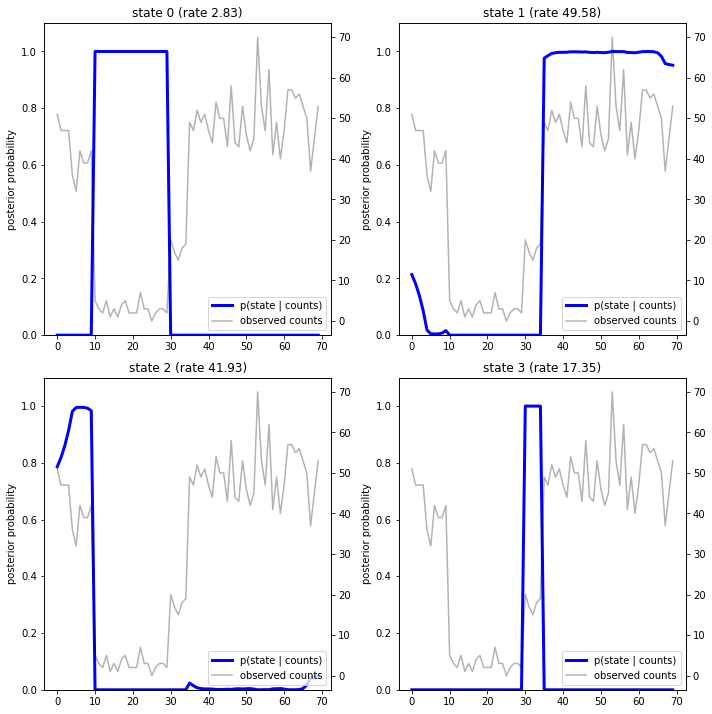
ในกรณี (อย่างง่าย) นี้ เราพบว่าแบบจำลองมักจะค่อนข้างมั่นใจ: ส่วนใหญ่ขั้นตอนจะกำหนดมวลความน่าจะเป็นทั้งหมดให้กับหนึ่งในสี่สถานะ โชคดีที่คำอธิบายดูสมเหตุสมผล!
นอกจากนี้เรายังสามารถเห็นภาพหลังนี้ในแง่ของอัตราที่เกี่ยวข้องกับรัฐแฝงไปได้มากที่สุดในแต่ละ timestep, ควบแน่นหลังน่าจะเป็นคำอธิบายเดียว:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
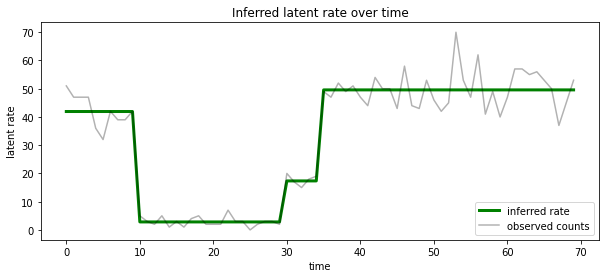
ไม่ทราบจำนวนรัฐ
ในปัญหาจริง เราอาจไม่ทราบจำนวนสถานะ 'จริง' ในระบบที่เรากำลังสร้างแบบจำลอง สิ่งนี้อาจไม่ใช่ข้อกังวลเสมอไป: หากคุณไม่สนใจเกี่ยวกับข้อมูลระบุตัวตนของรัฐที่ไม่รู้จักเป็นพิเศษ คุณสามารถเรียกใช้แบบจำลองที่มีสถานะมากกว่าที่คุณรู้ว่าแบบจำลองนั้นต้องการ และเรียนรู้ (เช่น) สำเนาจำนวนมาก สำเนาของรัฐที่แท้จริง แต่สมมติว่าคุณสนใจเกี่ยวกับการอนุมานจำนวนสถานะแฝง 'จริง'
เราสามารถดูนี้เป็นกรณีของ เบส์เลือกรูปแบบ : เรามีชุดของรุ่นผู้สมัครแต่ละคนมีจำนวนแตกต่างกันของรัฐแฝงและเราต้องการที่จะเลือกหนึ่งที่มีแนวโน้มที่จะมีการสร้างข้อมูลที่สังเกต การทำเช่นนี้เราจะคำนวณความน่าจะเป็นชายขอบของข้อมูลในแต่ละรุ่น (เรายังสามารถเพิ่มก่อนในรูปแบบของตัวเอง แต่ที่จะไม่จำเป็นในการวิเคราะห์นี้นั้น มีดโกนคชกรรมสาธารณรัฐโคลัมเบีย จะเปิดออกจะเพียงพอที่จะเข้ารหัส ชอบรุ่นที่เรียบง่ายกว่า)
แต่น่าเสียดายที่โอกาสร่อแร่จริงซึ่งรวมทั้งรัฐไม่ต่อเนื่อง \(z_{1:T}\) และ (เวกเตอร์) พารามิเตอร์อัตรา \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) ไม่ซูฮกสำหรับรุ่นนี้ เพื่อความสะดวกของเราจะใกล้เคียงโดยใช้สิ่งที่เรียกว่า " เบส์เชิงประจักษ์ " หรือ "พิมพ์ครั้งที่สองสูงสุดน่าจะเป็น" คาด: แทนอย่างบูรณาการออกพารามิเตอร์ (ไม่ทราบ) อัตรา \(\lambda\) เกี่ยวข้องกับแต่ละสถานะของระบบเราจะเพิ่มประสิทธิภาพ มากกว่าค่าของพวกเขา:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
การประมาณนี้อาจเกินจริง กล่าวคือ จะชอบโมเดลที่ซับซ้อนมากกว่าความเป็นไปได้ที่แท้จริง เราอาจจะพิจารณาประมาณซื่อสัตย์มากขึ้นเช่นการเพิ่มประสิทธิภาพการแปรผันขอบเขตล่างหรือใช้ Monte Carlo ประมาณการเช่น การสุ่มตัวอย่างสำคัญอบ ; สิ่งเหล่านี้ (น่าเศร้า) อยู่นอกเหนือขอบเขตของสมุดบันทึกนี้ (สำหรับข้อมูลเพิ่มเติมเกี่ยวคชกรรมเลือกรูปแบบและใกล้เคียง, บทที่ 7 ของยอดเยี่ยม เครื่องเรียนรู้: กน่าจะเป็นมุมมอง คือการอ้างอิงที่ดี.)
ในหลักการที่เราสามารถทำได้เปรียบเทียบรูปแบบนี้ได้ง่ายๆโดยการเพิ่มประสิทธิภาพ rerunning ข้างต้นหลายครั้งที่มีค่าที่แตกต่างของ num_states แต่ที่จะทำงานมาก ที่นี่เราจะแสดงวิธีการที่จะต้องพิจารณาหลายรูปแบบในแบบคู่ขนานโดยใช้ TFP ของ batch_shape กลไกสำหรับการ vectorization
เมทริกซ์การเปลี่ยนแปลงและสถานะเริ่มต้นก่อน: มากกว่าการสร้างคำอธิบายรูปแบบเดียวตอนนี้เราจะสร้างชุดของการฝึกอบรมการเปลี่ยนแปลงและ logits ก่อนที่หนึ่งสำหรับผู้สมัครแต่ละรุ่นได้ถึง max_num_states เพื่อให้ง่ายต่อการจัดชุด เราจะต้องตรวจสอบให้แน่ใจว่าการคำนวณทั้งหมดมี 'รูปร่าง' เหมือนกัน: สิ่งนี้จะต้องสอดคล้องกับขนาดของแบบจำลองที่ใหญ่ที่สุดที่เราจะพอดี ในการจัดการโมเดลขนาดเล็ก เราสามารถ 'ฝัง' คำอธิบายของโมเดลเหล่านั้นในมิติบนสุดของพื้นที่สถานะ โดยถือว่ามิติที่เหลือเป็นสถานะจำลองที่ไม่เคยใช้อย่างมีประสิทธิภาพ
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
ตอนนี้เราดำเนินการในทำนองเดียวกันกับข้างต้น ในครั้งนี้เราจะใช้มิติชุดพิเศษในการ trainable_rates แยกพอดีกับอัตราสำหรับแต่ละรุ่นภายใต้การพิจารณา
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
ในการคำนวณบันทึกปัญหาทั้งหมด เราระมัดระวังที่จะรวมเฉพาะค่าก่อนหน้าสำหรับอัตราที่ใช้จริงโดยส่วนประกอบแต่ละรุ่น:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
ตอนนี้เราเพิ่มประสิทธิภาพวัตถุประสงค์ชุดที่เราได้สร้างแบบจำลองที่เหมาะสมของผู้สมัครทั้งหมดพร้อมกัน:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
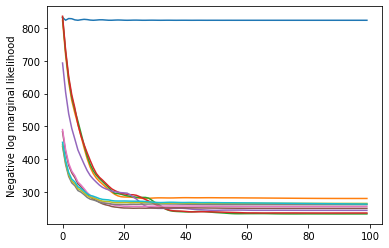
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
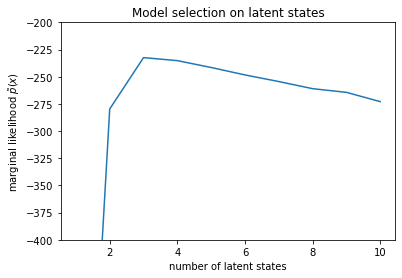
จากการตรวจสอบความน่าจะเป็น เราจะเห็นว่าความเป็นไปได้ส่วนเพิ่ม (โดยประมาณ) มีแนวโน้มที่จะชอบแบบจำลองสามสถานะ ดูเหมือนว่าจะค่อนข้างเป็นไปได้ -- โมเดล 'จริง' มีสี่สถานะ แต่จากการดูข้อมูลเพียงอย่างเดียว ยากที่จะแยกแยะคำอธิบายสามสถานะออก
นอกจากนี้เรายังสามารถแยกอัตราที่เหมาะสมสำหรับแต่ละรุ่นของผู้สมัคร:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
และพล็อตคำอธิบายที่แต่ละโมเดลจัดเตรียมไว้สำหรับข้อมูล:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
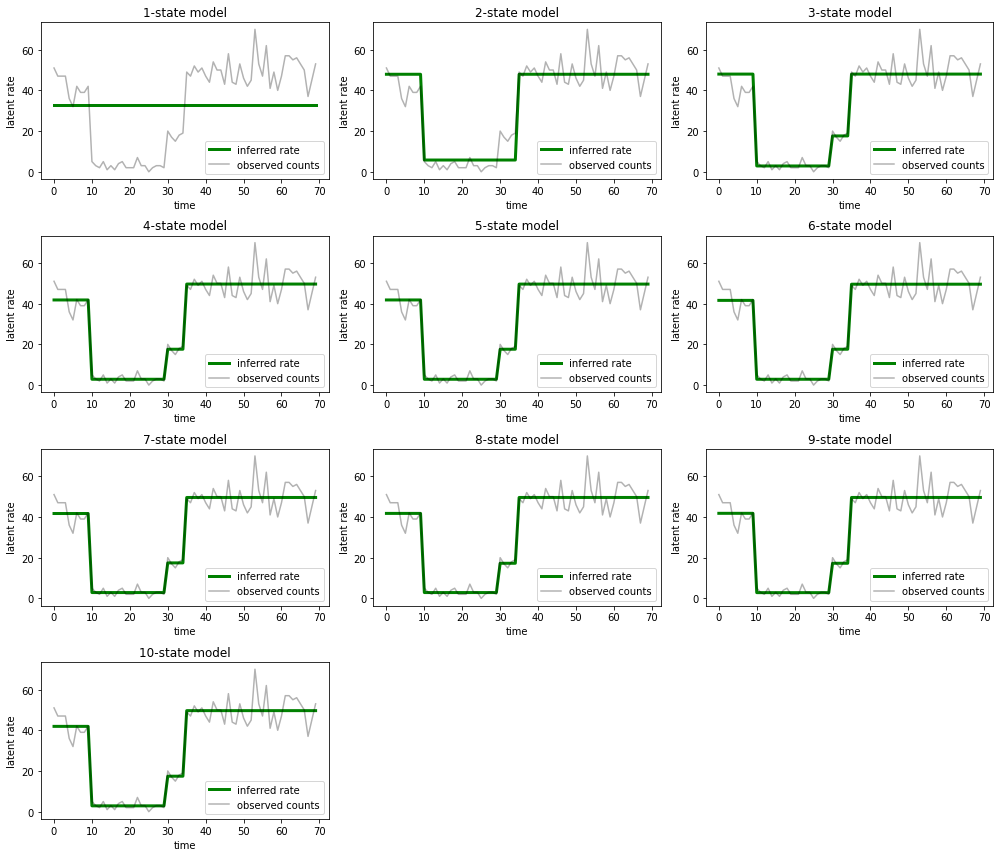
ง่ายที่จะเห็นว่าแบบจำลองสามสถานะแบบหนึ่ง สอง และ (แบบละเอียดมากขึ้น) ให้คำอธิบายที่ไม่เพียงพอได้อย่างไร ที่น่าสนใจคือ โมเดลทั้งหมดที่อยู่เหนือสถานะทั้งสี่ให้คำอธิบายเดียวกันโดยพื้นฐานแล้ว! อาจเป็นเพราะ 'ข้อมูล' ของเราค่อนข้างสะอาดและเหลือที่ว่างเล็กน้อยสำหรับคำอธิบายทางเลือก สำหรับข้อมูลในโลกแห่งความเป็นจริงที่ยุ่งเหยิง เราคาดหวังว่าโมเดลที่มีความจุสูงกว่าจะให้ข้อมูลที่พอดีกับข้อมูลมากขึ้นเรื่อยๆ โดยมีจุดแลกเปลี่ยนที่ความพอดีที่ปรับปรุงแล้วจะมีน้ำหนักเกินจากความซับซ้อนของแบบจำลอง
ส่วนขยาย
โมเดลในโน้ตบุ๊กนี้สามารถขยายได้โดยตรงในหลาย ๆ ด้าน ตัวอย่างเช่น:
- อนุญาตให้สถานะแฝงมีความน่าจะเป็นต่างกัน (บางสถานะอาจพบได้บ่อยและหายาก)
- อนุญาตให้มีการเปลี่ยนสถานะที่ไม่สม่ำเสมอระหว่างสถานะแฝง (เช่น เพื่อเรียนรู้ว่าการขัดข้องของเครื่องมักจะตามมาด้วยการรีบูตระบบ มักจะตามด้วยช่วงเวลาของประสิทธิภาพที่ดี เป็นต้น)
- รุ่นที่ปล่อยก๊าซเรือนกระจกอื่น ๆ เช่น
NegativeBinomialรูปแบบกระจายในข้อมูลการนับหรือการกระจายอย่างต่อเนื่องที่แตกต่างกันเช่นNormalสำหรับข้อมูลจริงมูลค่า
