Seleção de modelo bayesiano
 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Importações
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Tarefa: detecção de ponto de mudança com vários pontos de mudança
Considere uma tarefa de detecção de ponto de mudança: os eventos acontecem em uma taxa que muda ao longo do tempo, impulsionados por mudanças repentinas no estado (não observado) de algum sistema ou processo que gera os dados.
Por exemplo, podemos observar uma série de contagens como a seguinte:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
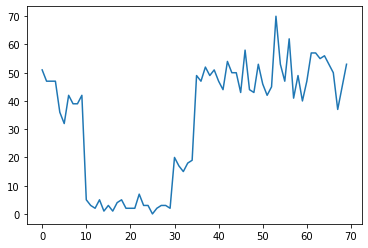
Eles podem representar o número de falhas em um datacenter, número de visitantes em uma página da web, número de pacotes em um link de rede, etc.
Observe que não é totalmente aparente quantos regimes de sistema distintos existem apenas de olhar para os dados. Você pode dizer onde ocorre cada um dos três pontos de mudança?
Número conhecido de estados
Consideraremos primeiro o caso (talvez irreal) em que o número de estados não observados é conhecido a priori. Aqui, presumiríamos que sabemos que existem quatro estados latentes.
Nós modelar este problema como uma (não homogéneo) processo de Poisson de comutação: em cada ponto no tempo, o número de eventos que ocorrem é distribuição de Poisson, e a taxa de acontecimentos é determinada pelo estado do sistema não observada \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Os estados latentes são discretos: \(z_t \in \{1, 2, 3, 4\}\), assim \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) é um vector simples contendo uma taxa de Poisson para cada estado. Para modelar a evolução de estados ao longo do tempo, vamos definir um simples modelo de transição \(p(z_t | z_{t-1})\): digamos que a cada passo que permanecer no estado anterior com alguma probabilidade \(p\), e com probabilidade \(1-p\) nós transição para uma estado diferente uniformemente ao acaso. O estado inicial também é escolhido uniformemente ao acaso, então temos:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Estes pressupostos correspondem a um modelo de Markov escondido com emissões de Poisson. Nós podemos codificá-los na PTF usando tfd.HiddenMarkovModel . Primeiro, definimos a matriz de transição e a anterior uniforme no estado inicial:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Em seguida, vamos construir um tfd.HiddenMarkovModel distribuição, usando uma variável treinável para representar as taxas associadas a cada estado do sistema. Parametrizamos as taxas no espaço de log para garantir que tenham valor positivo.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Finalmente, definimos densidade total de registo do modelo, incluindo uma lognormal fracamente-informativo prévia sobre as taxas, e executar um optimizador para calcular o máximo, a posteriori, o ajuste (MAP) para os dados de contagem observada.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
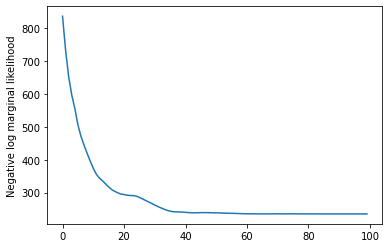
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Funcionou! Observe que os estados latentes neste modelo são identificáveis apenas até a permutação, então as taxas que recuperamos estão em uma ordem diferente e há um pouco de ruído, mas geralmente eles combinam muito bem.
Recuperando a trajetória do estado
Agora que ajustar o modelo, podemos querer reconstruir qual estado o modelo acredita que o sistema estava em em cada iteração.
Esta é uma tarefa inferência posterior: dadas as contagens observadas \(x_{1:T}\) e parâmetros do modelo (taxas) \(\lambda\), queremos inferir a sequência de variáveis latentes discretas, após a distribuição a posteriori \(p(z_{1:T} | x_{1:T}, \lambda)\). Em um modelo de Markov oculto, podemos calcular com eficiência os marginais e outras propriedades dessa distribuição usando algoritmos de passagem de mensagens padrão. Em particular, o posterior_marginals método irá calcular eficientemente (utilizando o algoritmo para a frente e para trás ), a distribuição de probabilidade marginal \(p(Z_t = z_t | x_{1:T})\) sobre o estado latente discreta \(Z_t\) em cada instante temporal \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Traçando as probabilidades posteriores, recuperamos a "explicação" do modelo sobre os dados: em quais momentos cada estado está ativo?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
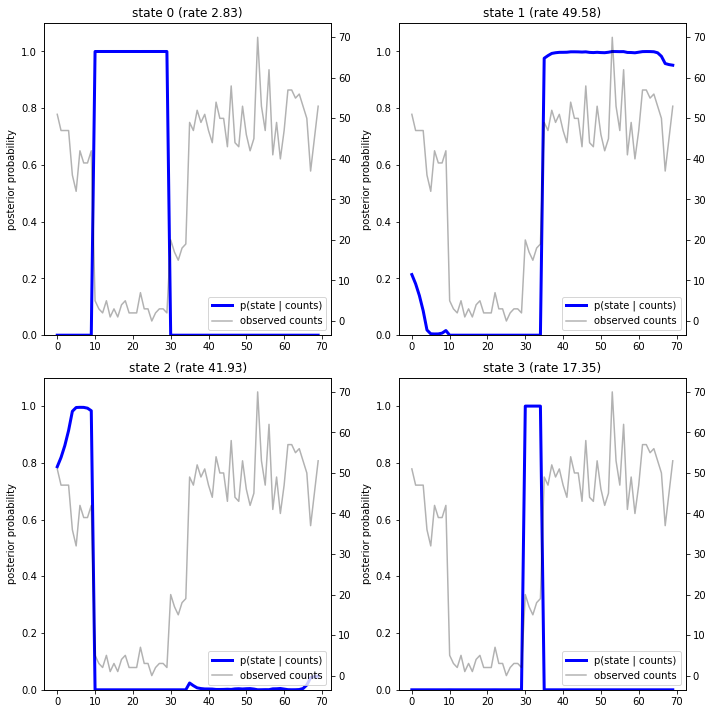
Nesse caso (simples), vemos que o modelo costuma ser bastante confiável: na maioria dos passos de tempo, ele atribui essencialmente toda a massa de probabilidade a um único dos quatro estados. Felizmente, as explicações parecem razoáveis!
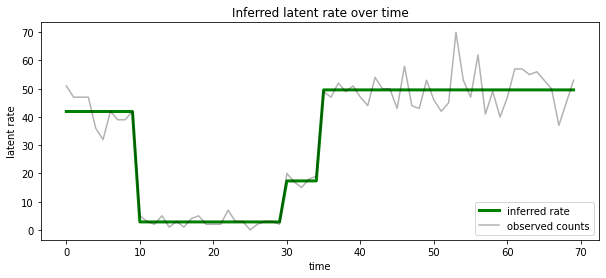
Também pode visualizar esta posterior em termos da taxa associada com o estado latente mais provável em cada iteração, condensando o posterior probabilística em uma única explicação:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
Número desconhecido de estados
Em problemas reais, podemos não saber o número 'verdadeiro' de estados no sistema que estamos modelando. Isso pode nem sempre ser uma preocupação: se você não se preocupa particularmente com as identidades dos estados desconhecidos, pode simplesmente executar um modelo com mais estados do que você sabe que o modelo vai precisar e aprender (algo como) um monte de duplicatas cópias dos estados reais. Mas vamos supor que você se preocupe em inferir o número 'verdadeiro' de estados latentes.
Podemos ver isso como um caso de selecção do modelo Bayesian : temos um conjunto de modelos candidatos, cada um com um número diferente de estados latentes, e queremos escolher o que é mais provável que geraram os dados observados. Para fazer isso, calculamos a probabilidade marginal dos dados no âmbito de cada modelo (que também poderia adicionar uma prévia sobre os próprios modelos, mas isso não será necessário nesta análise, a navalha de Bayesian Occam acaba por ser suficiente para codificar um preferência por modelos mais simples).
Infelizmente, a verdadeira probabilidade marginal, que integra mais de ambos os estados discretos \(z_{1:T}\) eo (vetor de) Parâmetros taxa \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) não é tratável para este modelo. Por conveniência, vamos aproximar-lo usando um dos chamados " Bayes empírico " ou "digitar máxima II probabilidade" estima: em vez de integrar plenamente os parâmetros (desconhecido) de taxa de \(\lambda\) associado a cada estado do sistema, vamos otimizar sobre seus valores:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Esta aproximação pode super ajustar, ou seja, ele irá preferir modelos mais complexos do que a verdadeira probabilidade marginal faria. Poderíamos considerar aproximações mais fiel, por exemplo, a optimização de um variacional limite inferior, ou usando um estimador de Monte Carlo, tais como amostragem importância recozido ; estes estão (infelizmente) além do escopo deste caderno. (Para mais informações sobre a selecção do modelo Bayesian e aproximações, o capítulo 7 do excelente Aprendizado de Máquina: uma perspectiva probabilística é uma boa referência.)
Em princípio, poderíamos fazer esta comparação modelo simplesmente executando novamente a otimização acima muitas vezes com diferentes valores de num_states , mas isso seria um monte de trabalho. Aqui vamos mostrar como considerar vários modelos em paralelo, usando da TFP batch_shape mecanismo para vetorização.
Matriz de transição e estado inicial antes: ao invés de construir uma única descrição do modelo, agora vamos construir um lote de matrizes de transição e logits anteriores, um para cada modelo candidato até max_num_states . Para facilitar o envio em lote, precisaremos garantir que todos os cálculos tenham a mesma 'forma': isso deve corresponder às dimensões do maior modelo que ajustaremos. Para lidar com modelos menores, podemos 'embutir' suas descrições nas dimensões superiores do espaço de estado, tratando efetivamente as dimensões restantes como estados fictícios que nunca são usados.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Agora procedemos da mesma forma que acima. Desta vez, vamos usar uma dimensão de lote extra na trainable_rates para atender separadamente as taxas para cada modelo em consideração.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Ao calcular o log prob total, tomamos o cuidado de somar apenas as anteriores para as taxas realmente usadas por cada componente do modelo:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Agora vamos alcançar o objectivo de lote que já construída, cabendo todos os modelos candidatos em simultâneo:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
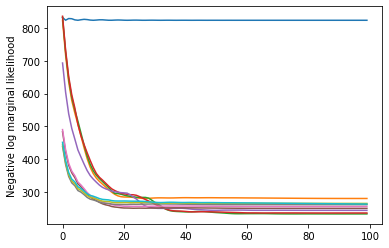
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
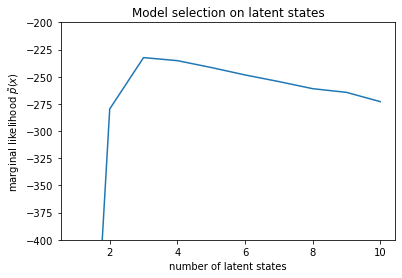
Examinando as probabilidades, vemos que a probabilidade marginal (aproximada) tende a preferir um modelo de três estados. Isso parece bastante plausível - o modelo "verdadeiro" tinha quatro estados, mas apenas olhando os dados é difícil descartar uma explicação de três estados.
Também podemos extrair as taxas de ajuste para cada modelo candidato:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
E plote as explicações que cada modelo fornece para os dados:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
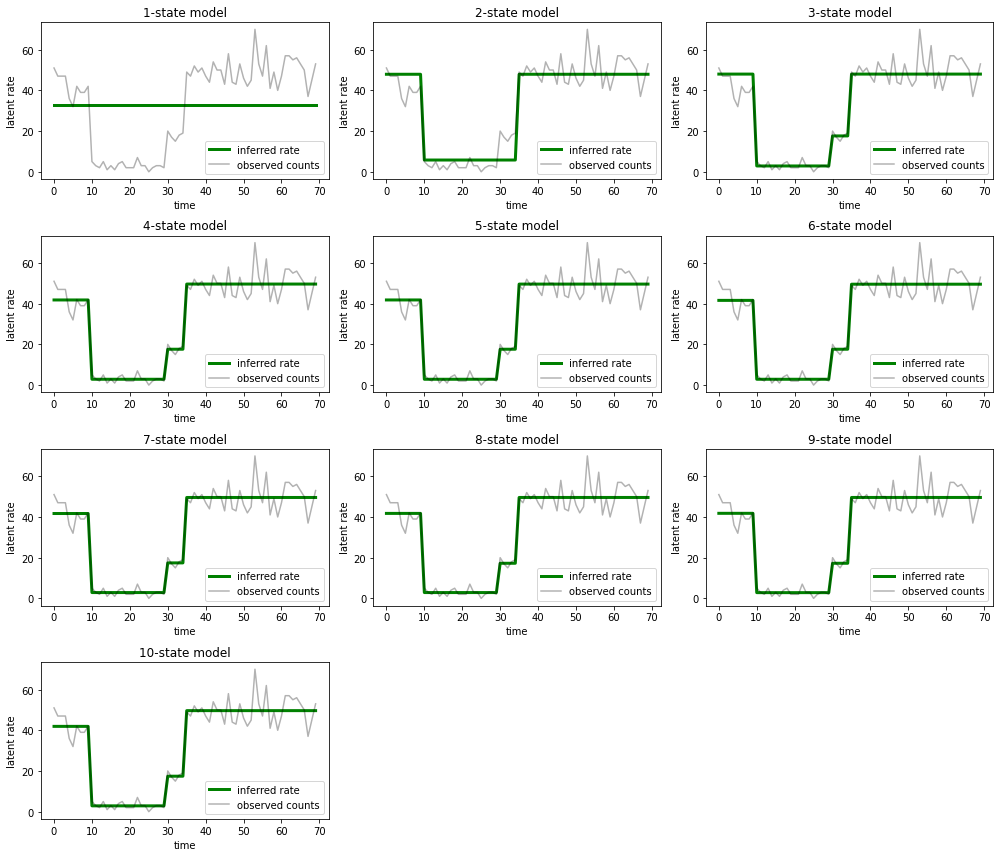
É fácil ver como os modelos de um, dois e (mais sutilmente) três estados fornecem explicações inadequadas. Curiosamente, todos os modelos acima de quatro estados fornecem essencialmente a mesma explicação! Isso provavelmente ocorre porque nossos 'dados' são relativamente limpos e deixam pouco espaço para explicações alternativas; em dados mais confusos do mundo real, esperaríamos que os modelos de maior capacidade fornecessem ajustes progressivamente melhores aos dados, com algum ponto de compensação em que o ajuste aprimorado é superado pela complexidade do modelo.
Extensões
Os modelos deste notebook podem ser estendidos diretamente de várias maneiras. Por exemplo:
- permitindo que estados latentes tenham probabilidades diferentes (alguns estados podem ser comuns versus raros)
- permitir transições não uniformes entre estados latentes (por exemplo, aprender que uma falha da máquina geralmente é seguida por uma reinicialização do sistema geralmente seguida por um período de bom desempenho, etc.)
- outros modelos de emissão, por exemplo
NegativeBinomialpara modelar variando dispersões em dados de contagem, ou distribuições contínuas, tais comoNormalpara os dados de valor real.
