Wybór modelu bayesowskiego
 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Import
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Zadanie: wykrywanie punktu zmiany z wieloma punktami zmiany
Rozważ zadanie wykrywania punktu zmiany: zdarzenia zachodzą w tempie, które zmienia się w czasie, napędzane przez nagłe zmiany (nieobserwowanego) stanu jakiegoś systemu lub procesu generującego dane.
Na przykład możemy zaobserwować serię zliczeń, jak poniżej:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
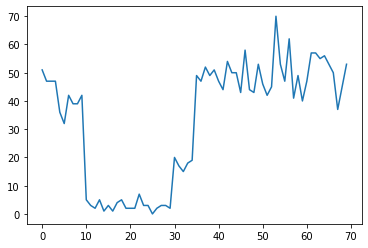
Mogą one reprezentować liczbę awarii w centrum danych, liczbę odwiedzających stronę internetową, liczbę pakietów w łączu sieciowym itp.
Zauważ, że nie jest do końca jasne, ile jest różnych reżimów systemowych, patrząc tylko na dane. Czy możesz powiedzieć, gdzie znajduje się każdy z trzech punktów przełączania?
Znana liczba stanów
Najpierw rozważymy (być może nierealistyczny) przypadek, w którym liczba nieobserwowanych stanów jest znana a priori. Tutaj założymy, że wiemy, że istnieją cztery stany ukryte.
Możemy modelować ten problem jako przełączania (niejednorodnego procesu Poissona): w każdym punkcie w czasie, liczba zdarzeń, które występują Poissona jest dystrybuowany, a tempo wydarzeń jest określana przez niedotrzymanego stanu systemu \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Stany utajone są dyskretne: \(z_t \in \{1, 2, 3, 4\}\)tak \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) jest prosty wektor zawierający współczynnik Poissona dla każdego stanu. Do modelowania ewolucji stanów w czasie, będziemy definiować prosty model przejściowy \(p(z_t | z_{t-1})\): powiedzmy, że na każdym kroku możemy zatrzymać się w poprzednim stanie z pewnym prawdopodobieństwem \(p\)iz prawdopodobieństwem \(1-p\) my przejście do inny stan równomiernie losowo. Stan początkowy jest również wybierany jednostajnie losowo, więc mamy:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Założenia te odpowiadają ukrytego modelu Markowa z emisji Poissona. Możemy zakodować je w TFP użyciu tfd.HiddenMarkovModel . Najpierw definiujemy macierz przejścia i ujednoliconą przed na stanie początkowym:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Następnie budujemy tfd.HiddenMarkovModel dystrybucji, wykorzystując zmienną nadającego się do reprezentowania stawki związane z każdym stanie systemu. Parametryzujemy stawki w przestrzeni logarytmicznej, aby zapewnić ich dodatnią wartość.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Wreszcie możemy określić całkowitą gęstość dziennika modelki, w tym lognormal słabo informacyjny wcześniejszej sprawie stawek i uruchomić optymalizatora aby obliczyć maksymalna a posteriori (MAP) dopasowanie do obserwowanego danych policzyć.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
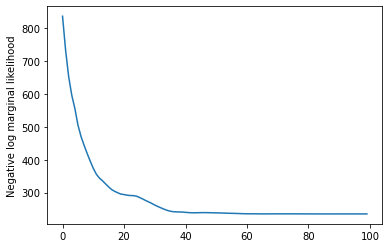
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Zadziałało! Zwróć uwagę, że stany ukryte w tym modelu można zidentyfikować tylko do permutacji, więc odzyskane współczynniki są w innej kolejności i jest trochę szumu, ale generalnie pasują one całkiem dobrze.
Odzyskiwanie trajektorii stanu
Teraz, gdy mamy dopasować model, może chcemy zrekonstruować stan model który uważa, że system był w każdym kroku to co.
Jest to zadanie posterior wnioskowanie: biorąc pod uwagę obserwowane liczy \(x_{1:T}\) i parametrów modelu (stóp) \(\lambda\), chcemy wyprowadzić sekwencję dyskretnych zmiennych ukrytych, po tylnej dystrybucji \(p(z_{1:T} | x_{1:T}, \lambda)\). W ukrytym modelu Markowa możemy wydajnie obliczyć marginesy i inne właściwości tego rozkładu przy użyciu standardowych algorytmów przekazywania wiadomości. W szczególności posterior_marginals metoda skutecznie obliczyć (przy użyciu do przodu do tyłu algorytm ) krańcowy rozkład prawdopodobieństwa \(p(Z_t = z_t | x_{1:T})\) nad dyskretnej utajonego stanu \(Z_t\) przy każdym kroku to \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
Wykreślając prawdopodobieństwa a posteriori, odzyskujemy „wyjaśnienie” danych z modelu: w którym momencie każdy stan jest aktywny?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
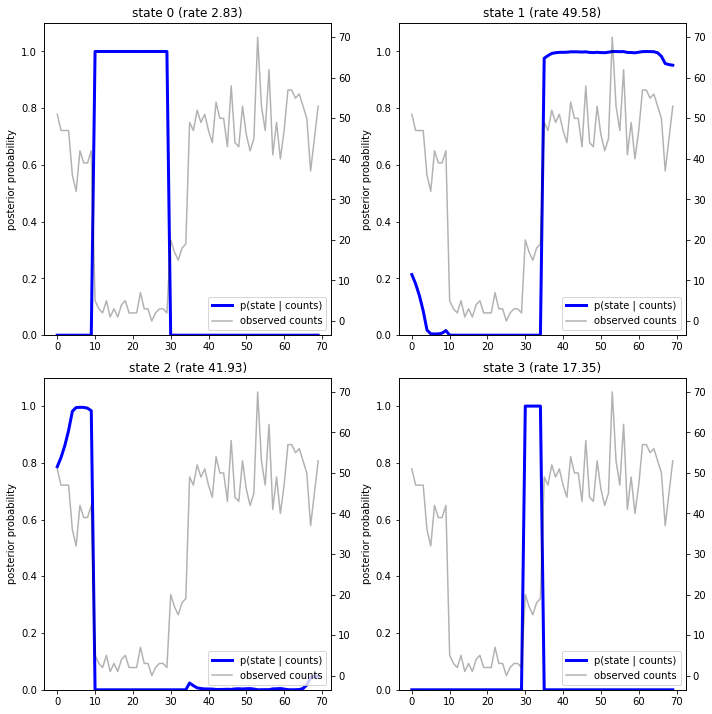
W tym (prostym) przypadku widzimy, że model jest zwykle dość pewny: w większości przedziałów czasowych przypisuje zasadniczo całą masę prawdopodobieństwa do jednego z czterech stanów. Na szczęście wyjaśnienia wyglądają rozsądnie!
Możemy również wyobrazić ten posterior pod względem szybkości związanej z najprawdopodobniej stanie utajonym na każdym kroku to, kondensacji probabilistyczną posterior w jednym wyjaśnienie:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
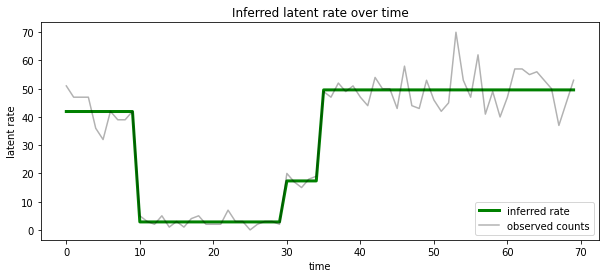
Nieznana liczba stanów
W rzeczywistych problemach możemy nie znać „prawdziwej” liczby stanów w modelowanym systemie. Nie zawsze może to stanowić problem: jeśli nie zależy Ci szczególnie na tożsamościach nieznanych stanów, możesz po prostu uruchomić model z większą liczbą stanów, niż wiesz, że model będzie potrzebować i nauczyć się (coś w stylu) kilku duplikatów kopie stanów faktycznych. Załóżmy jednak, że zależy Ci na wywnioskowaniu „prawdziwej” liczby stanów ukrytych.
Możemy uznać to za przypadek doboru modelu Bayesa : mamy zbiór modeli kandydujących, każdy z innej liczby stanów ukrytych i chcemy, aby wybrać ten, który jest najbardziej prawdopodobne, że wygenerowany obserwowanych danych. Aby to zrobić, możemy obliczyć marginalny prawdopodobieństwo danych pod każdym modelu (możemy też dodać przed na samych modeli, ale to nie będzie konieczne w tej analizie, w brzytwa Bayesa Ockhama okaże się wystarczająca do zakodowania preferowanie prostszych modeli).
Niestety, prawda marginalny prawdopodobieństwo, który integruje się zarówno na dyskretne stany \(z_{1:T}\) a (wektor) Parametry stopy \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) nie jest podatny na tym modelu. Dla wygody będziemy go zbliżyć pomocą tak zwanych „ Bayesa empirycznych ” lub „typ II” oszacowania największej wiarogodności: zamiast pełnej integracji z parametrów (nieznane) stóp \(\lambda\) związanego z każdego stanu systemu, będziemy optymalizować ponad ich wartościami:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Przybliżenie to może przesadzać, tj. będzie preferować bardziej złożone modele niż prawdziwe marginalne prawdopodobieństwo. Można rozważyć wierniejszymi aproksymacji, na przykład optymalizacja wariacyjnej dolna granica, lub za pomocą Monte Carlo estymatora takie jak wyżarzaniu próbek znaczenie ; są one (niestety) poza zakresem tego zeszytu. (Więcej informacji na temat doboru modelu Bayesa i przybliżeń, rozdziału 7 doskonałej uczenia maszynowego: probabilistyczny Perspektywa jest odniesienie dobry).
W zasadzie moglibyśmy zrobić to porównanie modelu po prostu przez ponowne uruchomienie optymalizacji powyżej wiele razy z różnymi wartościami num_states , ale to byłoby dużo pracy. Tutaj pokażemy jak uważa wielu modeli równolegle, przy użyciu TFP za batch_shape mechanizm wektoryzacji.
Macierz transformacji i stan początkowy przed: zamiast budowania jednolitego opisu modelu, teraz będziemy budować partię macierzy przejścia i wcześniejszych logits, po jednym dla każdego modelu kandydata aż do max_num_states . Aby ułatwić tworzenie partii, musimy upewnić się, że wszystkie obliczenia mają ten sam „kształt”: musi to odpowiadać wymiarom największego modelu, który zmieścimy. Aby obsłużyć mniejsze modele, możemy „osadzić” ich opisy w najwyższych wymiarach przestrzeni stanów, efektywnie traktując pozostałe wymiary jako stany atrapy, które nigdy nie są używane.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Teraz postępujemy podobnie jak powyżej. Tym razem użyjemy dodatkowy wymiar wsadowego w trainable_rates osobno dopasować stawki dla każdego modelu pod uwagę.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Przy obliczaniu całkowitego logarytmicznego prob, staramy się sumować tylko a priori dla współczynników faktycznie stosowanych przez każdy składnik modelu:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Teraz możemy zoptymalizować cel partii mamy skonstruowany, pasuje do wszystkich modeli kandydujące jednocześnie:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
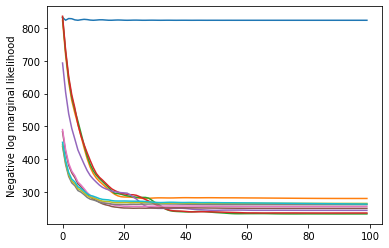
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
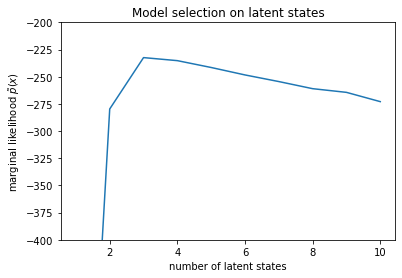
Badając prawdopodobieństwa, widzimy, że (przybliżona) marginalna prawdopodobieństwo preferuje model trójstanowy. Wydaje się to całkiem prawdopodobne – „prawdziwy” model miał cztery stany, ale patrząc na dane, trudno wykluczyć wyjaśnienie trójstanowe.
Możemy również wyodrębnić stawki pasujące do każdego modelu kandydującego:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
I wykreśl wyjaśnienia, które każdy model dostarcza dla danych:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
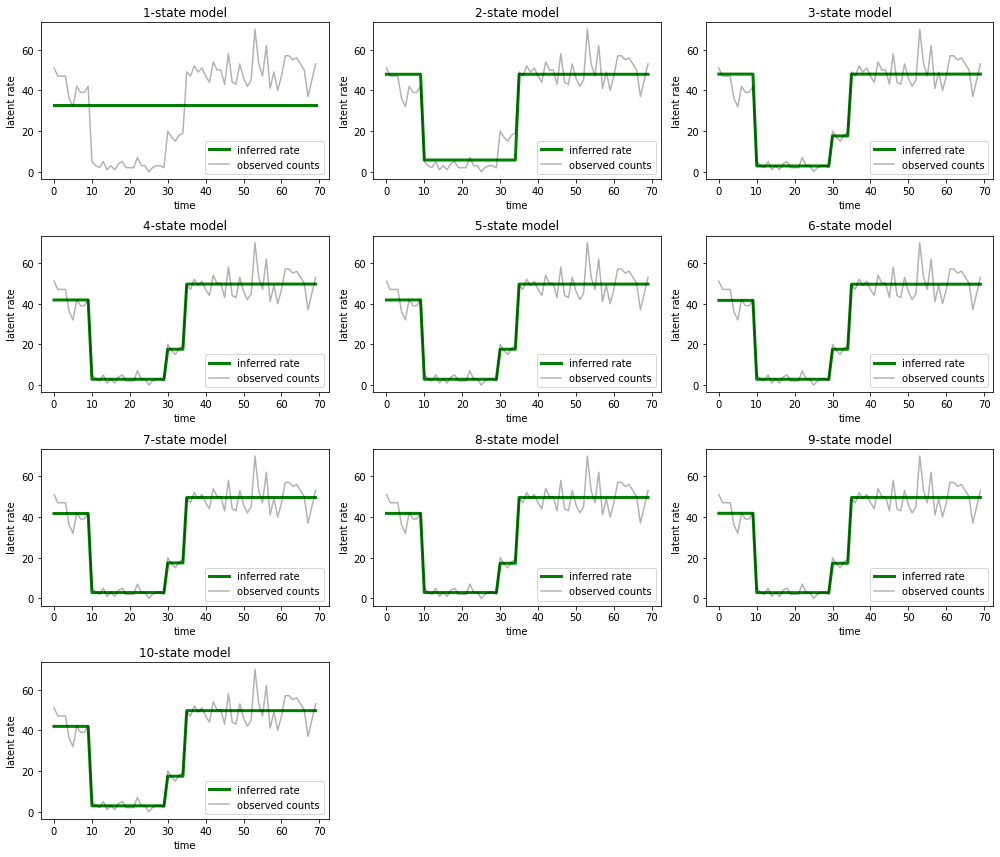
Łatwo zauważyć, że modele jedno-, dwu- i (bardziej subtelnie) trójstanowe dostarczają nieodpowiednich wyjaśnień. Co ciekawe, wszystkie modele powyżej czterech stanów dostarczają zasadniczo tego samego wyjaśnienia! Jest tak prawdopodobnie dlatego, że nasze „dane” są stosunkowo czyste i pozostawiają niewiele miejsca na alternatywne wyjaśnienia; na bardziej nieuporządkowanych danych rzeczywistych spodziewalibyśmy się, że modele o większej pojemności będą zapewniać coraz lepsze dopasowanie do danych, z pewnym kompromisem, w którym lepsze dopasowanie jest równoważone złożonością modelu.
Rozszerzenia
Modele w tym notebooku można było w prosty sposób rozbudować na wiele sposobów. Na przykład:
- zezwalanie stanom utajonym na różne prawdopodobieństwa (niektóre stany mogą być powszechne lub rzadkie)
- umożliwienie niejednorodnych przejść między stanami ukrytymi (np. aby dowiedzieć się, że po awarii komputera zwykle następuje ponowne uruchomienie systemu, po którym zwykle następuje okres dobrej wydajności itp.)
- inne modele emisji, np
NegativeBinomialmodelować różnej dyspersji w danych dotyczących ilości lub rozkładów ciągłych, takich jakNormaldanych o wartościach rzeczywistych.
