बायेसियन मॉडल चयन
 TensorFlow.org पर देखें TensorFlow.org पर देखें |  Google Colab में चलाएं Google Colab में चलाएं |  GitHub पर स्रोत देखें GitHub पर स्रोत देखें |  नोटबुक डाउनलोड करें नोटबुक डाउनलोड करें |
आयात
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
कार्य: कई परिवर्तन बिंदुओं के साथ परिवर्तन बिंदु का पता लगाना
एक परिवर्तन बिंदु पहचान कार्य पर विचार करें: घटनाएं उस दर पर होती हैं जो समय के साथ बदलती हैं, जो डेटा उत्पन्न करने वाली किसी प्रणाली या प्रक्रिया की (अनदेखी) स्थिति में अचानक बदलाव से प्रेरित होती हैं।
उदाहरण के लिए, हम निम्नलिखित की तरह गिनती की एक श्रृंखला देख सकते हैं:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]

ये डेटासेंटर में विफलताओं की संख्या, वेबपेज पर आगंतुकों की संख्या, नेटवर्क लिंक पर पैकेटों की संख्या आदि का प्रतिनिधित्व कर सकते हैं।
ध्यान दें कि यह पूरी तरह से स्पष्ट नहीं है कि डेटा को देखने से ही कितने अलग सिस्टम शासन हैं। क्या आप बता सकते हैं कि तीनों स्विचपॉइंट में से प्रत्येक कहाँ होता है?
राज्यों की ज्ञात संख्या
हम पहले (शायद अवास्तविक) मामले पर विचार करेंगे, जहां अनदेखी राज्यों की संख्या को प्राथमिकता के रूप में जाना जाता है। यहाँ, हम मान लेंगे कि हम जानते हैं कि चार अव्यक्त अवस्थाएँ हैं।
हम एक स्विचिंग (inhomogeneous) प्वासों प्रक्रिया के रूप में इस समस्या को मॉडल: समय में प्रत्येक बिंदु पर, कि हो घटनाओं की संख्या प्वासों वितरित, और घटनाओं की दर अप्रत्यक्ष प्रणाली राज्य द्वारा निर्धारित किया जाता है \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
: अव्यक्त राज्यों असतत हैं \(z_t \in \{1, 2, 3, 4\}\), इसलिए \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) एक सरल प्रत्येक राज्य के लिए एक प्वासों दर युक्त वेक्टर है। समय के साथ राज्यों के विकास मॉडल करने के लिए, हम एक सरल संक्रमण मॉडल को परिभाषित करेंगे \(p(z_t | z_{t-1})\): मान लें कि प्रत्येक चरण में हम कुछ संभावना के साथ पहले वाली स्थिति में रहने \(p\)संभावना के साथ, और \(1-p\) हम एक के लिए संक्रमण अलग-अलग राज्य समान रूप से यादृच्छिक रूप से। प्रारंभिक अवस्था को भी यादृच्छिक रूप से समान रूप से चुना जाता है, इसलिए हमारे पास है:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
इन मान्यताओं के अनुरूप एक छिपा मार्कोव मॉडल प्वासों उत्सर्जन के साथ। हम का उपयोग कर TFP में उन्हें सांकेतिक शब्दों में बदलना कर सकते हैं tfd.HiddenMarkovModel । सबसे पहले, हम प्रारंभिक अवस्था से पहले संक्रमण मैट्रिक्स और वर्दी को परिभाषित करते हैं:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
इसके बाद, हम एक निर्माण tfd.HiddenMarkovModel वितरण, एक trainable चर का उपयोग कर प्रत्येक प्रणाली राज्य के साथ जुड़े दरों का प्रतिनिधित्व करने के लिए। हम यह सुनिश्चित करने के लिए लॉग-स्पेस में दरों का मापन करते हैं कि वे सकारात्मक-मूल्यवान हैं।
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
अंत में, हम मॉडल के कुल लॉग घनत्व को परिभाषित, एक कमजोर-सूचनात्मक lognormal दरों पर पहले भी शामिल है, और गणना करने के लिए एक अनुकूलक चलाने के अधिकतम का अनुमान किया मनाया गिनती आंकड़ों के (एमएपी) फिट।
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
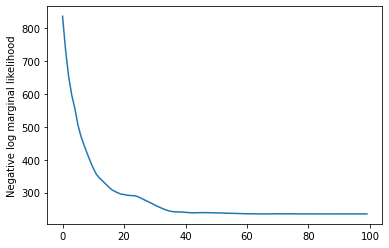
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
इसने काम कर दिया! ध्यान दें कि इस मॉडल में अव्यक्त अवस्थाओं को केवल क्रमपरिवर्तन तक ही पहचाना जा सकता है, इसलिए हमने जो दरें प्राप्त की हैं वे एक अलग क्रम में हैं, और थोड़ा शोर है, लेकिन आम तौर पर वे बहुत अच्छी तरह से मेल खाते हैं।
राज्य प्रक्षेपवक्र पुनर्प्राप्त करना
अब जब हम मॉडल फिट है, हम फिर से संगठित करने जो राज्य मॉडल का मानना है कि प्रणाली प्रत्येक timestep दौरान थी चाह सकते हैं।
यह एक पीछे अनुमान काम है: मनाया मायने रखता दिया \(x_{1:T}\) और (दर) मॉडल मापदंडों \(\lambda\), हम असतत अव्यक्त चर के अनुक्रम अनुमान लगाने के लिए चाहते हैं, पिछला वितरण निम्नलिखित \(p(z_{1:T} | x_{1:T}, \lambda)\)। एक छिपे हुए मार्कोव मॉडल में, हम मानक संदेश-पासिंग एल्गोरिदम का उपयोग करके इस वितरण के सीमांत और अन्य गुणों की कुशलता से गणना कर सकते हैं। विशेष रूप से, posterior_marginals विधि कुशलतापूर्वक (का उपयोग कर की गणना होगी आगे-पीछे एल्गोरिथ्म सीमांत संभावना वितरण) \(p(Z_t = z_t | x_{1:T})\) असतत अव्यक्त राज्य में \(Z_t\) प्रत्येक timestep पर \(t\)।
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
पिछली संभावनाओं को प्लॉट करते हुए, हम डेटा के मॉडल के "स्पष्टीकरण" को पुनर्प्राप्त करते हैं: प्रत्येक राज्य किस समय सक्रिय होता है?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
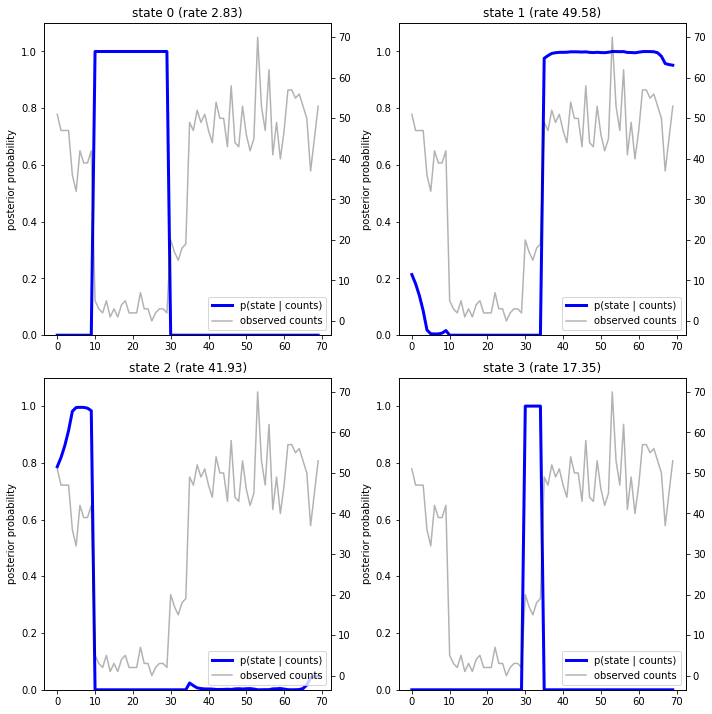
इस (सरल) मामले में, हम देखते हैं कि मॉडल आमतौर पर काफी आश्वस्त होता है: ज्यादातर समय-समय पर यह चार राज्यों में से एक को अनिवार्य रूप से सभी संभाव्यता द्रव्यमान प्रदान करता है। सौभाग्य से, स्पष्टीकरण उचित लगते हैं!
हम भी प्रत्येक timestep पर सबसे अधिक संभावना अव्यक्त राज्य के साथ जुड़े दर के मामले में इस पीछे कल्पना कर सकते हैं, एक भी स्पष्टीकरण में संभाव्य पीछे संघनक:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
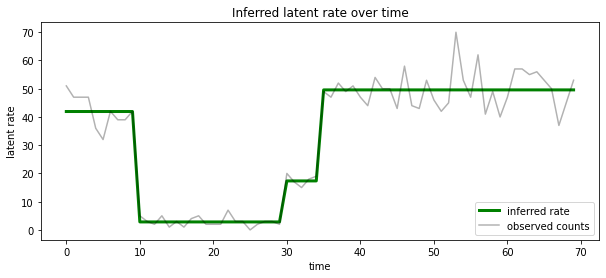
राज्यों की अज्ञात संख्या
वास्तविक समस्याओं में, हम उस प्रणाली में राज्यों की 'सच्ची' संख्या नहीं जान सकते हैं जो हम मॉडलिंग कर रहे हैं। यह हमेशा चिंता का विषय नहीं हो सकता है: यदि आप विशेष रूप से अज्ञात राज्यों की पहचान के बारे में परवाह नहीं करते हैं, तो आप मॉडल की आवश्यकता से अधिक राज्यों के साथ एक मॉडल चला सकते हैं, और सीखें (कुछ ऐसा) डुप्लिकेट का एक गुच्छा वास्तविक राज्यों की प्रतियां। लेकिन आइए मान लें कि आप गुप्त राज्यों की 'सत्य' संख्या का अनुमान लगाने की परवाह करते हैं।
हम के एक मामले के रूप में यह देख सकते हैं बायेसियन मॉडल चयन : हम अव्यक्त राज्यों की एक अलग संख्या के साथ प्रत्येक उम्मीदवार मॉडल का एक सेट, है, और हम एक है कि सबसे अधिक संभावना है मनाया डेटा उत्पन्न की है, चुनना चाहते हैं। ऐसा करने के लिए, हम प्रत्येक मॉडल के तहत डेटा के सीमांत संभावना की गणना (हम भी मॉडल अपने आप पर एक पूर्व जोड़ सकता है, लेकिन वह इस विश्लेषण में आवश्यक नहीं होगा, बायेसियन Occam के रेजर पता चला है एनकोड एक के लिए पर्याप्त होना करने के लिए सरल मॉडल के प्रति वरीयता)।
दुर्भाग्य से, सच सीमांत संभावना है, जो दोनों के ऊपर जुड़ता है असतत राज्यों \(z_{1:T}\) और (के वेक्टर) दर मापदंडों \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) नहीं इस मॉडल के लिए विनयशील है। सुविधा के लिए, हम इसे एक तथाकथित "का उपयोग कर अनुमानित करेंगे अनुभवजन्य Bayes " या "टाइप द्वितीय अधिकतम संभावना" अनुमान: के बजाय पूरी तरह से (अज्ञात) दर मापदंडों बाहर को एकीकृत करने की \(\lambda\) प्रत्येक प्रणाली राज्य के साथ जुड़े, हम अनुकूलित कर देंगे उनके मूल्यों पर:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
यह सन्निकटन ओवरफिट हो सकता है, अर्थात, यह वास्तविक सीमांत संभावना की तुलना में अधिक जटिल मॉडल पसंद करेगा। हम और अधिक वफादार अनुमानों, जैसे विचार कर सकते हैं, के अनुकूलन एक बाध्य निचले परिवर्तन संबंधी, या एक मोंटे कार्लो आकलनकर्ता इस तरह के रूप में उपयोग कर annealed महत्व नमूने ; ये (दुख की बात है) इस नोटबुक के दायरे से बाहर हैं। (बायेसियन मॉडल चयन और अनुमानों, उत्कृष्ट के 7 अध्याय के बारे में अधिक के लिए मशीन लर्निंग: एक संभाव्य परिप्रेक्ष्य एक अच्छा संदर्भ है।)
सिद्धांत रूप में, हम बस के विभिन्न मूल्यों के साथ कई बार ऊपर अनुकूलन का पुनर्प्रसारण द्वारा इस मॉडल तुलना कर सकता है num_states , लेकिन वह बहुत काम किया जाएगा। यहाँ हम कैसे समानांतर में एक से अधिक मॉडल पर विचार करना, TFP का उपयोग दिखाता हूँ batch_shape vectorization के लिए तंत्र।
संक्रमण मैट्रिक्स और प्रारंभिक अवस्था से पहले: इसके बजाए एक ही मॉडल विवरण के निर्माण की तुलना में, अब हम संक्रमण मैट्रिक्स और पूर्व logits, करने के लिए प्रत्येक उम्मीदवार मॉडल के लिए एक का एक बैच का निर्माण करेंगे max_num_states । आसान बैचिंग के लिए हमें यह सुनिश्चित करना होगा कि सभी संगणनाओं का 'आकार' समान हो: यह हमारे द्वारा फिट किए जाने वाले सबसे बड़े मॉडल के आयामों के अनुरूप होना चाहिए। छोटे मॉडलों को संभालने के लिए, हम उनके विवरणों को स्टेट स्पेस के सबसे ऊपरी आयामों में 'एम्बेड' कर सकते हैं, शेष आयामों को प्रभावी रूप से डमी स्टेट्स के रूप में मानते हुए जिनका कभी उपयोग नहीं किया जाता है।
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
अब हम ऊपर की तरह ही आगे बढ़ते हैं। इस बार हम में एक अतिरिक्त बैच आयाम इस्तेमाल करेंगे trainable_rates अलग से विचार किया जा रहा एक मॉडल के लिए दरों में फिट करने के लिए।
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
कुल लॉग समस्या की गणना में, हम प्रत्येक मॉडल घटक द्वारा वास्तव में उपयोग की जाने वाली दरों के लिए केवल पुजारियों का योग करने के लिए सावधान हैं:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
अब हम बैच उद्देश्य हम निर्माण किया गया है अनुकूलन, एक साथ सभी उम्मीदवार मॉडल फिटिंग:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')

num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')

संभावनाओं की जांच करते हुए, हम देखते हैं कि (अनुमानित) सीमांत संभावना तीन-राज्य मॉडल को पसंद करती है। यह काफी प्रशंसनीय लगता है - 'सच्चे' मॉडल में चार राज्य थे, लेकिन केवल डेटा को देखने से तीन-राज्य स्पष्टीकरण को खारिज करना मुश्किल है।
हम प्रत्येक उम्मीदवार मॉडल के लिए उपयुक्त दरों को भी निकाल सकते हैं:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
और उन स्पष्टीकरणों को प्लॉट करें जो प्रत्येक मॉडल डेटा के लिए प्रदान करता है:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
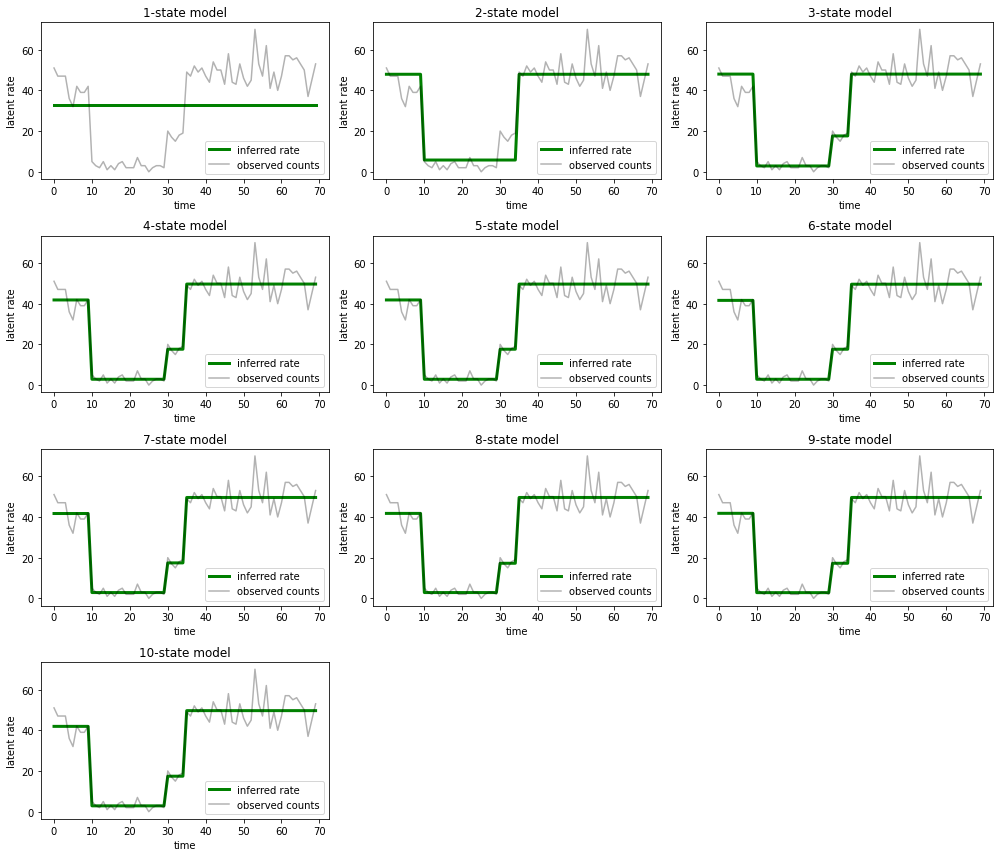
यह देखना आसान है कि कैसे एक-, दो- और (अधिक सूक्ष्म रूप से) तीन-राज्य मॉडल अपर्याप्त स्पष्टीकरण प्रदान करते हैं। दिलचस्प बात यह है कि चार राज्यों से ऊपर के सभी मॉडल अनिवार्य रूप से एक ही व्याख्या प्रदान करते हैं! यह संभव है क्योंकि हमारा 'डेटा' अपेक्षाकृत साफ है और वैकल्पिक स्पष्टीकरण के लिए बहुत कम जगह छोड़ता है; गड़बड़ वास्तविक दुनिया के डेटा पर हम उम्मीद करेंगे कि उच्च क्षमता वाले मॉडल डेटा को उत्तरोत्तर बेहतर फिट प्रदान करेंगे, कुछ ट्रेडऑफ़ बिंदु के साथ जहां बेहतर फिट मॉडल जटिलता से अधिक है।
एक्सटेंशन
इस नोटबुक के मॉडल को कई तरह से सीधा बढ़ाया जा सकता है। उदाहरण के लिए:
- अव्यक्त राज्यों को अलग-अलग संभावनाओं की अनुमति देना (कुछ राज्य सामान्य बनाम दुर्लभ हो सकते हैं)
- अव्यक्त अवस्थाओं के बीच गैर-समान संक्रमण की अनुमति देना (उदाहरण के लिए, यह जानने के लिए कि मशीन क्रैश के बाद आमतौर पर सिस्टम रीबूट होता है, आमतौर पर अच्छे प्रदर्शन की अवधि के बाद होता है, आदि)
- अन्य उत्सर्जन मॉडल, जैसे
NegativeBinomialजैसे गिनती डेटा, या सतत वितरण में dispersions अलग मॉडल करने के लिएNormalवास्तविक मूल्य डेटा के लिए।
