בחירת דגמים בייסיאניים
 הצג באתר TensorFlow.org הצג באתר TensorFlow.org |  הפעל בגוגל קולאב הפעל בגוגל קולאב |  צפה במקור ב-GitHub צפה במקור ב-GitHub |  הורד מחברת הורד מחברת |
יבוא
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
משימה: זיהוי נקודות שינוי עם מספר נקודות שינוי
שקול משימת זיהוי נקודת שינוי: אירועים מתרחשים בקצב המשתנה לאורך זמן, מונע על ידי שינויים פתאומיים במצב (שלא נצפה) של מערכת או תהליך כלשהו המייצר את הנתונים.
לדוגמה, אנו עשויים לראות סדרה של ספירות כמו הבאות:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
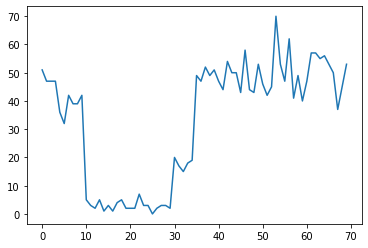
אלה יכולים לייצג את מספר הכשלים במרכז הנתונים, מספר המבקרים בדף אינטרנט, מספר מנות בקישור רשת וכו'.
שימו לב, זה לא לגמרי ברור כמה משטרי מערכת שונים יש רק מהסתכלות על הנתונים. האם אתה יכול לדעת היכן מתרחשת כל אחת משלושת נקודות המעבר?
מספר מדינות ידוע
תחילה נשקול את המקרה (אולי לא מציאותי) שבו מספר המצבים הבלתי נצפים ידוע אפריורי. כאן, היינו מניחים שאנחנו יודעים שיש ארבעה מצבים סמויים.
אנחנו מודל לבעיה זו כתהליך מיתוג (הומוגניות) פואסון: בכל נקודת זמן, מספר האירועים המתרחשים הוא פואסון מבוזרת, ושיעור אירועים נקבעת לפי מצב המערכת נצפים \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
קובעים הסמוי הם דיסקרטיים: \(z_t \in \{1, 2, 3, 4\}\), כך \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) הוא פשוט וקטור המכיל שיעור פואסון עבור כול מדינה. כדי לדמות את האבולוציה של מדינות לאורך זמן, נגדיר מודל פשוט המעבר \(p(z_t | z_{t-1})\): נניח כי בכל צעד שאנו להישאר במצב הקודם עם כמה ההסתברות \(p\), ועם הסתברות \(1-p\) המעבר שאנחנו לבית מצב שונה באופן אחיד באקראי. גם המצב ההתחלתי נבחר באופן אחיד באקראי, אז יש לנו:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
הנחות אלו מתאימות ל מודל מרקוב נסתר עם פליטת פואסון. אנחנו יכולים לקודד אותם TFP באמצעות tfd.HiddenMarkovModel . ראשית, אנו מגדירים את מטריצת המעבר ואת הקוד האחיד על המצב ההתחלתי:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
הבא, אנו בונים tfd.HiddenMarkovModel ההפצה, באמצעות משתנה שאפשר לאלף לייצג את שיעורי הקשורים לכל מצב המערכת. אנו מפרמטרים את התעריפים ב-log-space כדי להבטיח שהם בעלי ערך חיובי.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
לבסוף, אנו מגדירים את צפיפות היומן הכוללת של המודל, לרבות lognormal בחולשה-אינפורמטיבי לפני על השיעורים, ולהפעיל האופטימיזציה כדי לחשב את המקסימום בדיעבד (MAP) הותאם לנתון ספירת הנצפה.
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
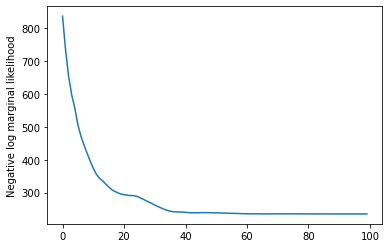
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
זה עבד! שימו לב שהמצבים הסמויים במודל הזה ניתנים לזיהוי רק עד לתמורה, כך שהקצבים ששחזרנו הם בסדר שונה, ויש קצת רעש, אבל בדרך כלל הם תואמים די טוב.
שיקום מסלול המדינה
עכשיו הכנסנו למודל, נרצה לשחזר הקובע את המודל מאמין במערכת הייתה בכול timestep.
זוהי משימת היקש אחורית: בהינתן ספירת נצפה \(x_{1:T}\) ופרמטרי מודל (שיעורים) \(\lambda\), אנחנו רוצים להסיק את הרצף של משתנים חבויים דיסקרטיים, בעקבות חלוק האחורית \(p(z_{1:T} | x_{1:T}, \lambda)\). במודל מרקוב נסתר, אנו יכולים לחשב ביעילות שוליים ומאפיינים אחרים של התפלגות זו באמצעות אלגוריתמים סטנדרטיים להעברת הודעות. בפרט, posterior_marginals השיטה תהיה לחשב באופן יעיל (באמצעות האלגוריתם קדימה-אחורה ) את התפלגות הסתברות השולית \(p(Z_t = z_t | x_{1:T})\) רחבי המדינה הסמוי הדיסקרטי \(Z_t\) בכול timestep \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
משרטטים את ההסתברויות האחוריות, אנו משחזרים את ה"הסבר" של המודל לנתונים: באילו נקודות זמן כל מצב פעיל?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
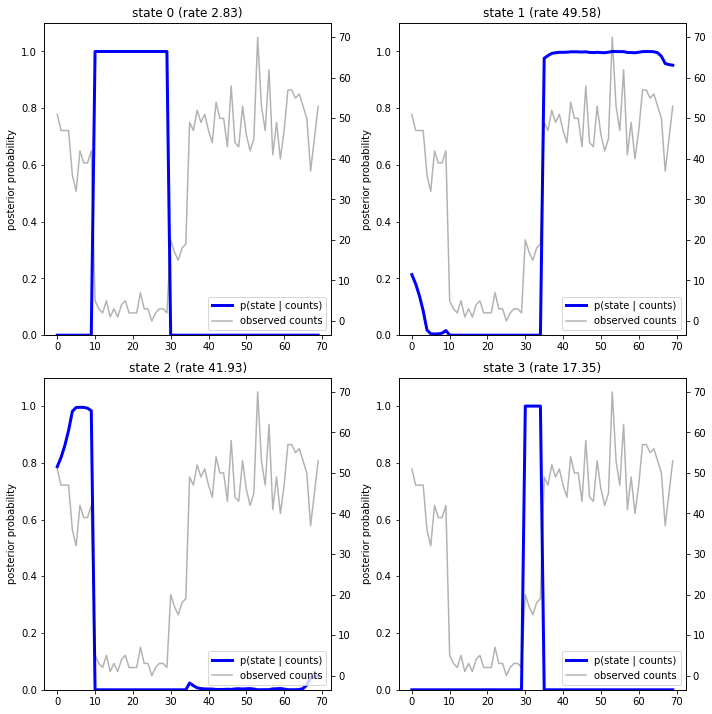
במקרה (פשוט) זה, אנו רואים שהמודל הוא בדרך כלל די בטוח: ברוב שלבי הזמן הוא מקצה למעשה את כל מסת ההסתברות לאחד מארבעת המצבים. למרבה המזל, ההסברים נראים הגיוניים!
אנחנו יכולים גם לדמיין אחוריים הזה במונחים של השיעור המשויך למצב הרדום כנראה בכול timestep, עיבוי האחורי הסתברותית לתוך הסבר יחיד:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
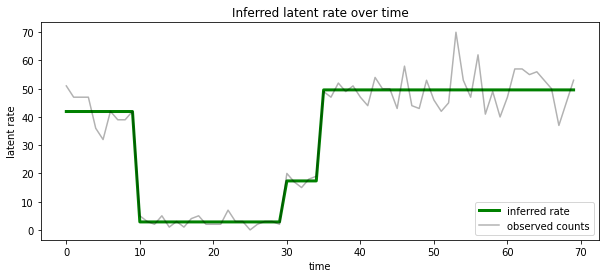
מספר לא ידוע של מדינות
בבעיות אמיתיות, ייתכן שאיננו יודעים את המספר ה"אמיתי" של המצבים במערכת שאנו מעצבים. זה אולי לא תמיד מדאיג: אם לא אכפת לך במיוחד מהזהות של המדינות הלא ידועות, אתה יכול פשוט להריץ מודל עם יותר מצבים ממה שאתה יודע שהמודל יצטרך, וללמוד (משהו כמו) חבורה של כפילויות עותקים של המצבים בפועל. אבל בוא נניח שאכפת לך מהסקת המספר ה'אמיתי' של המצבים הסמויים.
אנחנו יכולים להציג את זה כמקרה של בחירת מודל בייס : יש לנו קבוצה של מודלים מועמדים, כול אחד עם מספר שונה של מדינות סמויות, ואנחנו רוצים לבחור את האחד כי הוא ככל הנראה הוא זה שיצר את נתון נצפה. לשם כך, אנו מחשבים את הסיכוי השולי של הנתונים תחת כול דגם (אנחנו גם יכולים להוסיף לפני על המודלים עצמם, אבל זה לא יהיה צורך בניתוח זה, את מכונת הגילוח של בייס אוקאם יתברר מספיק כדי לקודד העדפה לדגמים פשוטים יותר).
למרבה הצער, את הסבירות השולית נכון, המשלבת מעל הן המדינות הדיסקרטיות \(z_{1:T}\) ואת (הווקטור של) פרמטרי שיעור \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) הוא לא צייתן עבור דגם זה. לנוחיותכם, נצטרך אותו בקירוב באמצעות מה שמכונה " בייס אמפירי " או "סוג II הסיכוי המרבי" אומדן: במקום לשלב באופן מלא את הפרמטרים שיעור (לא ידוע) \(\lambda\) הקשורים לכל מצב המערכת, נבצע אופטימיזציה על הערכים שלהם:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
קירוב זה עשוי להתאים יתר על המידה, כלומר, הוא יעדיף דגמים מורכבים יותר מאשר הסבירות השולית האמיתית. אנחנו יכולים לשקול קירובים נאמנים יותר, למשל, אופטימיזציה של וריאצית חסם התחתון, או באמצעות מונטה קרלו הערכה כגון דגימת חשיבות מרותקת ; אלה (למרבה הצער) מעבר לתחום המחברת הזו. (למידע נוסף על בחירת המודל בייס ו קירובים, פרק 7 של מעולה למידת מכונה: פרספקטיבה הסתברותי הוא התייחסות טובה.)
באופן עקרוני, אנחנו יכולים לעשות השוואת המודל הזה פשוט על ידי והפעלה מחדש של אופטימיזציה מעל פעמים רבות עם ערכים שונים של num_states , אבל זה יהיה הרבה עבודה. במאמר זה נדגים כיצד לשקול מודלים מרובים במקביל, באמצעות של הפריון הכולל batch_shape מנגנון vectorization.
מטריצת המעבר ולפני המצב ההתחלתי: במקום לבנות תיאור מודל יחיד, עכשיו נצטרך לבנות קבוצה של מטריצות המעבר logits לפני, אחד עבור כל דגם מועמד עד max_num_states . בשביל אצווה קלה נצטרך לוודא שלכל החישובים יש את אותה 'צורה': זה חייב להתאים למידות הדגם הגדול ביותר שנתאים. כדי לטפל במודלים קטנים יותר, אנו יכולים 'להטמיע' את התיאורים שלהם בממדים העליונים ביותר של מרחב המצב, ולמעשה להתייחס לממדים הנותרים כמצבי דמה שלעולם אינם בשימוש.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
כעת אנו ממשיכים באופן דומה לעיל. הפעם נשתמש מימד אצווה תוספת trainable_rates בנפרד להתאים את שיעורי עבור כל דגם תחת שיקול.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
בחישוב ההסתברות הכוללת ביומן, אנו מקפידים לסכם רק את הקודמים עבור התעריפים המשמשים בפועל על ידי כל רכיב מודל:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
עכשיו אנחנו לייעל את המטרה אצווה שמנו בנוי, התאמת כל הדגמים המועמד בו זמנית:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
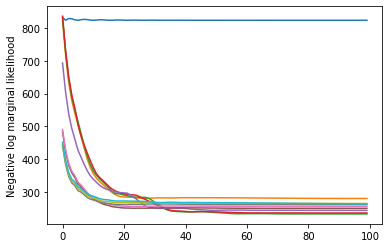
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
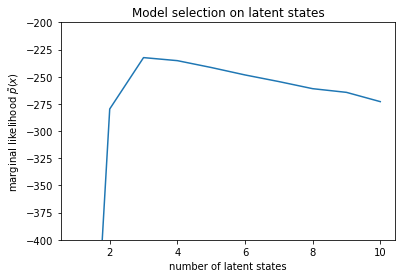
בבחינת ההסתברויות, אנו רואים שהסבירות השולית (בקירוב) נוטה להעדיף מודל של שלוש מדינות. זה נראה סביר למדי - למודל ה'אמיתי' היו ארבעה מצבים, אבל מעצם התבוננות בנתונים קשה לשלול הסבר של שלוש מדינות.
אנו יכולים גם לחלץ את התעריפים המתאימים לכל מודל מועמד:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
ותארו את ההסברים שכל מודל מספק לנתונים:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
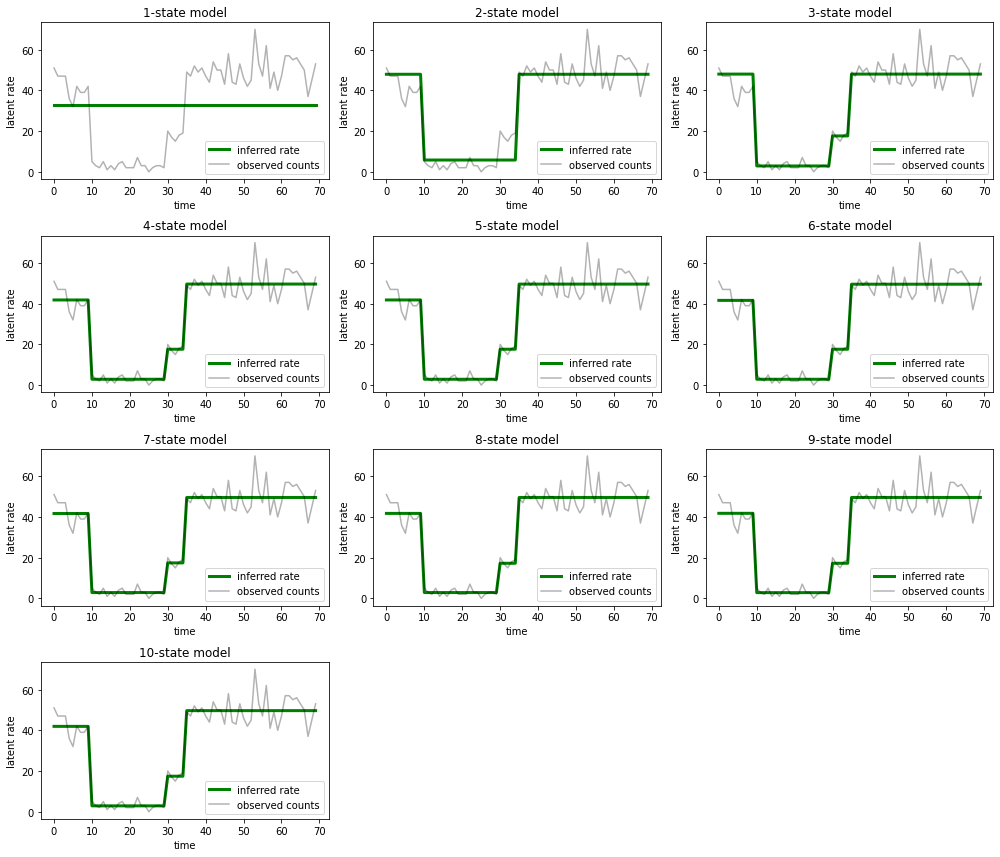
קל לראות כיצד המודלים של שלוש מדינות אחד, שתיים ו(באופן עדין יותר) מספקים הסברים לא מספקים. מעניין, כל הדגמים מעל ארבע מדינות מספקים בעצם את אותו הסבר! זה כנראה בגלל שה'נתונים' שלנו נקיים יחסית ומשאירים מעט מקום להסברים חלופיים; בנתונים מבולגנים יותר מהעולם האמיתי היינו מצפים שהמודלים בעלי הקיבולת הגבוהה יותר יספקו בהדרגה התאמה טובה יותר לנתונים, עם נקודת פשרה כלשהי שבה ההתאמה המשופרת גוברת על ידי מורכבות המודל.
הרחבות
ניתן להרחיב את הדגמים במחברת זו בצורה פשוטה בדרכים רבות. לדוגמה:
- מתן אפשרות למצבים סמויים להיות בעלי הסתברויות שונות (מצבים מסוימים עשויים להיות נפוצים לעומת נדירים)
- מתן אפשרות למעברים לא אחידים בין מצבים סמויים (לדוגמה, ללמוד שקריסת מכונה גוררת בדרך כלל אתחול מחדש של המערכת מלווה בדרך כלל תקופה של ביצועים טובים וכו')
- מודלי פליטה אחרים, למשל
NegativeBinomialלמדל משתנה תפוצות בנתוני ספירה, או הפצות רציפות כגוןNormalעבור נתונים בזמן מוערך.
