Sélection de modèles bayésiens
 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Importations
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
Tâche : détection de points de changement avec plusieurs points de changement
Considérons une tâche de détection de point de changement : les événements se produisent à une vitesse qui change au fil du temps, entraînée par des changements soudains dans l'état (non observé) d'un système ou d'un processus générant les données.
Par exemple, nous pourrions observer une série de décomptes comme les suivants :
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
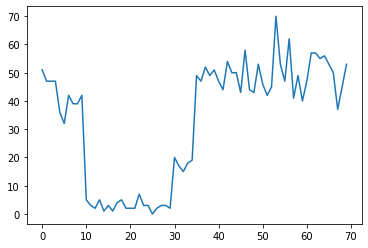
Ceux-ci peuvent représenter le nombre de pannes dans un centre de données, le nombre de visiteurs sur une page Web, le nombre de paquets sur un lien réseau, etc.
Notez qu'il n'est pas tout à fait évident combien de régimes de système distincts il y a juste en regardant les données. Pouvez-vous dire où se produit chacun des trois points de commutation ?
Nombre connu d'états
Considérons d'abord le cas (peut-être irréaliste) où le nombre d'états non observés est connu a priori. Ici, nous supposerions que nous savons qu'il existe quatre états latents.
Nous avons modélisé ce problème en commutation (inhomogène) processus de Poisson: à chaque point dans le temps, le nombre d'événements qui se produisent est une distribution de Poisson, et le taux d'événements est déterminé par l'état du système non observé \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
Les états latents sont discrets: \(z_t \in \{1, 2, 3, 4\}\), donc \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) est un vecteur simple contenant un taux de Poisson pour chaque état. Pour modéliser l'évolution des Etats au fil du temps, nous allons définir un modèle simple de transition \(p(z_t | z_{t-1})\): Disons que , à chaque étape , nous restons dans l'état précédent avec une certaine probabilité \(p\), et avec une probabilité \(1-p\) nous transition vers une état différent uniformément au hasard. L'état initial est également choisi uniformément au hasard, on a donc :
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
Ces hypothèses correspondent à un modèle de Markov caché avec des émissions de Poisson. Nous pouvons les encoder dans TFP en utilisant tfd.HiddenMarkovModel . Tout d'abord, nous définissons la matrice de transition et le prior uniforme sur l'état initial :
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
Ensuite, nous construisons une tfd.HiddenMarkovModel de distribution, en utilisant une variable trainable pour représenter les taux associés à chaque état du système. Nous paramétrons les taux dans l'espace journal pour nous assurer qu'ils sont à valeur positive.
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
Enfin, nous définissons la densité totale du journal du modèle, y compris un lognormales faiblement informatif avant sur les taux, et exécuter un optimiseur pour calculer le maximum a posteriori ajustement aux données de comptage observée (MAP).
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
Ça a marché! Notez que les états latents dans ce modèle ne sont identifiables que jusqu'à la permutation, donc les taux que nous avons récupérés sont dans un ordre différent, et il y a un peu de bruit, mais généralement ils correspondent assez bien.
Retrouver la trajectoire de l'état
Maintenant que nous avons adapter le modèle, nous pourrions établir quel état le modèle estime que le système était à chaque timestep.
Ceci est une tâche d'inférence postérieure: compte tenu des résultats observés \(x_{1:T}\) et les paramètres du modèle (taux) \(\lambda\), nous voulons déduire la séquence de variables latentes discrètes, suite à la distribution postérieure \(p(z_{1:T} | x_{1:T}, \lambda)\). Dans un modèle de Markov caché, nous pouvons calculer efficacement les marges et d'autres propriétés de cette distribution en utilisant des algorithmes de transmission de messages standard. En particulier, le posterior_marginals procédé calcule efficacement ( en utilisant l' algorithme avant-arrière ) la distribution de probabilité marginale \(p(Z_t = z_t | x_{1:T})\) sur l'état latent discret \(Z_t\) à chaque pas de temps \(t\).
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
En traçant les probabilités postérieures, nous récupérons « l'explication » des données du modèle : à quels instants chaque état est-il actif ?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
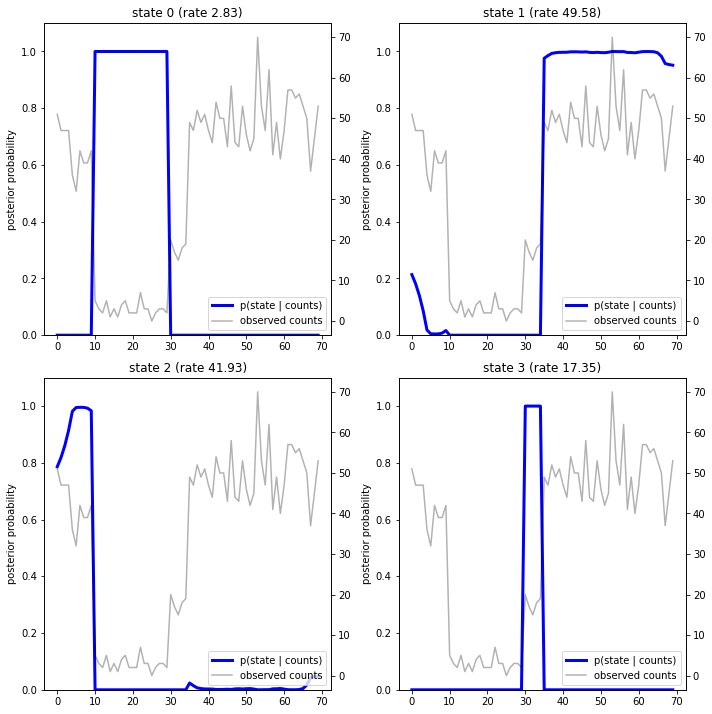
Dans ce cas (simple), nous voyons que le modèle est généralement assez confiant : à la plupart des pas de temps, il attribue essentiellement toute la masse de probabilité à un seul des quatre états. Heureusement, les explications ont l'air raisonnables !
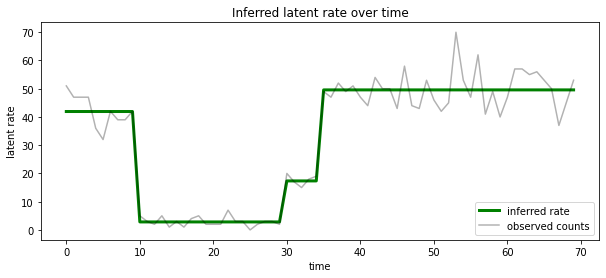
On peut aussi visualiser ce postérieur en termes de taux associé au plus l' état latent susceptible à chaque timestep, condensation postérieur probabiliste en une seule explication:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
Nombre d'états inconnu
Dans les problèmes réels, nous pouvons ne pas connaître le « vrai » nombre d'états dans le système que nous modélisons. Cela peut ne pas toujours être un problème : si vous ne vous souciez pas particulièrement de l'identité des états inconnus, vous pouvez simplement exécuter un modèle avec plus d'états que ce dont vous pensez avoir besoin, et apprendre (quelque chose comme) un tas de doublons copies des états réels. Mais supposons que vous vous souciez de déduire le "vrai" nombre d'états latents.
Nous pouvons considérer cela comme un cas de sélection de modèle bayésien : nous avons un ensemble de modèles candidats, chacun avec un nombre différent d'états latents, et nous voulons choisir celui qui est le plus susceptible d'avoir généré les données observées. Pour ce faire, on calcule la probabilité marginale des données dans chaque modèle (on peut aussi ajouter un préalable sur les modèles eux - mêmes, mais cela ne sera pas nécessaire dans cette analyse, le rasoir d'Occam bayésienne se révèle être suffisante pour coder une préférence pour des modèles plus simples).
Malheureusement, la probabilité réelle marginale, qui intègre à la fois sur les états discrets \(z_{1:T}\) et le (vecteur) paramètres de taux \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) n'est pas tractable pour ce modèle. Pour plus de commodité, nous rapprochons l'aide d' un soi-disant « Bayes empiriques » ou estimation « de type II de vraisemblance maximale »: au lieu d'intégrer pleinement les paramètres de vitesse (INCONNU) \(\lambda\) associée à chaque état du système, nous optimisons sur leurs valeurs :
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
Cette approximation peut surdimensionner, c'est-à-dire qu'elle préférera des modèles plus complexes que la vraie vraisemblance marginale. On pourrait envisager des approximations plus fidèles, par exemple, l' optimisation d' une VARIATIONNELLE borne inférieure, ou en utilisant un estimateur de Monte Carlo tels que l' échantillonnage d'importance recuite ; ceux-ci dépassent (malheureusement) le cadre de ce cahier. (Pour en savoir plus sur la sélection de modèle bayésien et approximations, chapitre 7 de l'excellent apprentissage machine: une perspective probabilistes est une bonne référence.)
En principe, nous pourrions faire cette comparaison du modèle simplement en réexécutant l'optimisation ci - dessus à plusieurs reprises avec des valeurs différentes de num_states , mais ce serait beaucoup de travail. Ici , nous allons montrer comment considérer plusieurs modèles en parallèle, en utilisant les TFP batch_shape mécanisme pour vectorisation.
Matrice de transition et de l' état initial avant: plutôt que de construire une seule description du modèle, maintenant , nous allons construire un lot de matrices de transition et logits avant, un pour chaque modèle candidat à max_num_states . Pour faciliter le traitement par lots, nous devrons nous assurer que tous les calculs ont la même « forme » : cela doit correspondre aux dimensions du plus grand modèle que nous allons adapter. Pour gérer des modèles plus petits, nous pouvons « intégrer » leurs descriptions dans les dimensions les plus élevées de l'espace d'états, en traitant efficacement les dimensions restantes comme des états fictifs qui ne sont jamais utilisés.
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
Maintenant, nous procédons de la même manière que ci-dessus. Cette fois , nous allons utiliser une dimension de lot supplémentaire dans trainable_rates pour tenir séparément les taux pour chaque modèle considéré.
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
Lors du calcul du log prob total, nous prenons soin de ne faire la somme que des a priori pour les taux réellement utilisés par chaque composante du modèle :
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
Maintenant , nous optimisons l'objectif de traitement par lots que nous avons construit et adapté à tous les modèles candidats simultanément:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
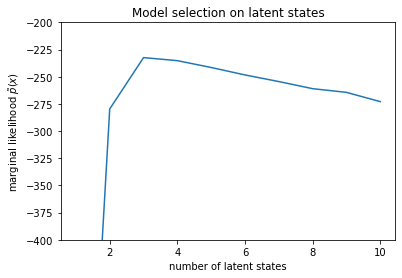
En examinant les vraisemblances, nous voyons que la vraisemblance marginale (approximative) tend à préférer un modèle à trois états. Cela semble tout à fait plausible - le "vrai" modèle avait quatre états, mais en examinant simplement les données, il est difficile d'exclure une explication à trois états.
Nous pouvons également extraire les taux adaptés à chaque modèle candidat :
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
Et tracez les explications que chaque modèle fournit pour les données :
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
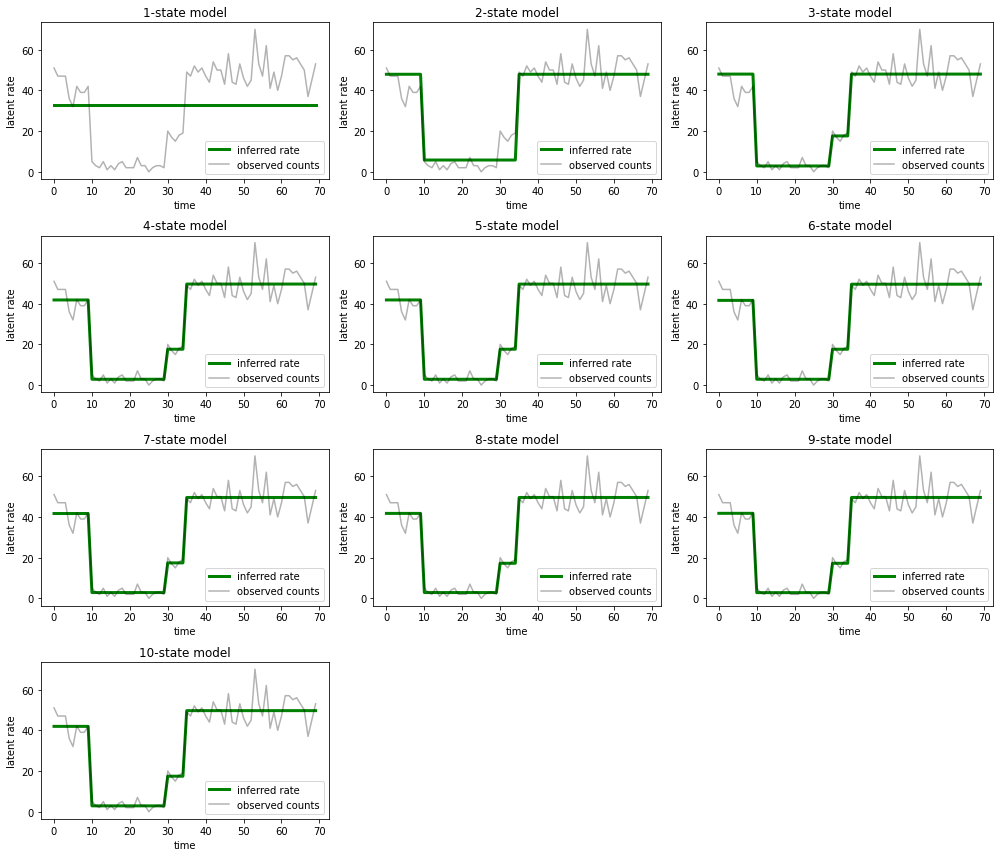
Il est facile de voir comment les modèles à un, deux et (plus subtilement) trois états fournissent des explications inadéquates. Fait intéressant, tous les modèles au-dessus de quatre états fournissent essentiellement la même explication ! Cela est probablement dû au fait que nos « données » sont relativement propres et laissent peu de place à des explications alternatives ; sur des données du monde réel plus compliquées, nous nous attendrions à ce que les modèles à plus grande capacité fournissent des ajustements progressivement meilleurs aux données, avec un certain compromis où l'ajustement amélioré est surpondéré par la complexité du modèle.
Rallonges
Les modèles de ce portable pourraient être facilement étendus de plusieurs manières. Par example:
- permettant aux états latents d'avoir des probabilités différentes (certains états peuvent être communs ou rares)
- permettre des transitions non uniformes entre les états latents (par exemple, apprendre qu'un plantage de la machine est généralement suivi d'un redémarrage du système est généralement suivi d'une période de bonnes performances, etc.)
- d' autres modèles d'émission, par exemple
NegativeBinomialpour modéliser différentes dispersions dans les données de comptage, ou des distributions telles que continousNormalpour les données à valeurs réelles.

