Bayesian মডেল নির্বাচন
 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
আমদানি
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
from matplotlib import pylab as plt
%matplotlib inline
import scipy.stats
টাস্ক: একাধিক চেঞ্জপয়েন্ট সহ চেঞ্জপয়েন্ট সনাক্তকরণ
একটি পরিবর্তনপয়েন্ট সনাক্তকরণ কাজ বিবেচনা করুন: ঘটনাগুলি এমন একটি হারে ঘটে যা সময়ের সাথে সাথে পরিবর্তিত হয়, কিছু সিস্টেমের (অনিরীক্ষিত) অবস্থায় হঠাৎ পরিবর্তনের দ্বারা চালিত হয় বা ডেটা তৈরি করার প্রক্রিয়া।
উদাহরণস্বরূপ, আমরা নিম্নলিখিতগুলির মতো গণনার একটি সিরিজ পর্যবেক্ষণ করতে পারি:
true_rates = [40, 3, 20, 50]
true_durations = [10, 20, 5, 35]
observed_counts = tf.concat(
[tfd.Poisson(rate).sample(num_steps)
for (rate, num_steps) in zip(true_rates, true_durations)], axis=0)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f7589bdae10>]
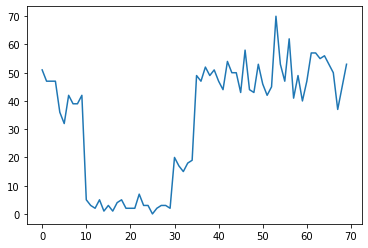
এটি একটি ডেটাসেন্টারে ব্যর্থতার সংখ্যা, একটি ওয়েবপৃষ্ঠায় দর্শকের সংখ্যা, একটি নেটওয়ার্ক লিঙ্কে প্যাকেটের সংখ্যা ইত্যাদি উপস্থাপন করতে পারে।
মনে রাখবেন যে শুধুমাত্র ডেটার দিকে তাকিয়ে কতগুলি স্বতন্ত্র সিস্টেম শাসন রয়েছে তা সম্পূর্ণরূপে স্পষ্ট নয়। আপনি কি বলতে পারেন যে তিনটি সুইচপয়েন্টের প্রতিটি কোথায় ঘটে?
রাজ্যের পরিচিত সংখ্যা
আমরা প্রথমে (সম্ভবত অবাস্তব) কেসটি বিবেচনা করব যেখানে অপ্রদর্শিত রাজ্যের সংখ্যা একটি অগ্রাধিকার হিসাবে পরিচিত। এখানে, আমরা ধরে নেব আমরা জানি চারটি সুপ্ত অবস্থা আছে।
আমরা একটি সুইচিং (inhomogeneous) পইসন প্রক্রিয়া হিসেবে এই সমস্যা মডেল: সময় প্রতিটি বিন্দুতে, যে ঘটতে ঘটনা সংখ্যা পইসন বিতরণ, এবং ঘটনা হার অলক্ষিত সিস্টেম রাষ্ট্র দ্বারা নির্ধারিত হয় \(z_t\):
\[x_t \sim \text{Poisson}(\lambda_{z_t})\]
: সুপ্ত রাজ্যের বিযুক্ত হয় \(z_t \in \{1, 2, 3, 4\}\), তাই \(\lambda = [\lambda_1, \lambda_2, \lambda_3, \lambda_4]\) একটি সহজ প্রতিটি রাষ্ট্রের জন্য একটি পইসন হার ধারণকারী বাহক। সময়ের সাথে রাজ্যের বিবর্তন মডেল করার জন্য, আমরা একটি সহজ রূপান্তরটি মডেল সংজ্ঞায়িত করব \(p(z_t | z_{t-1})\): ধরুন প্রতিটি পদে পদে আমরা কিছু সম্ভাবনা সঙ্গে পূর্বের অবস্থায় থাকতে দিন \(p\)সম্ভাব্যতা সঙ্গে, এবং \(1-p\) আমরা পরিবর্তনকে এলোমেলোভাবে অভিন্নভাবে বিভিন্ন রাষ্ট্র। প্রাথমিক অবস্থাও এলোমেলোভাবে অভিন্নভাবে নির্বাচিত হয়, তাই আমাদের আছে:
\[ \begin{align*} z_1 &\sim \text{Categorical}\left(\left\{\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right\}\right)\\ z_t | z_{t-1} &\sim \text{Categorical}\left(\left\{\begin{array}{cc}p & \text{if } z_t = z_{t-1} \\ \frac{1-p}{4-1} & \text{otherwise}\end{array}\right\}\right) \end{align*}\]
এই অনুমানের একটি মিলা গোপন মার্কভ মডেল পইসন নির্গমন সঙ্গে। আমরা ব্যবহার TFP তাদের এনকোড করতে tfd.HiddenMarkovModel । প্রথমত, আমরা প্রাথমিক অবস্থায় ট্রানজিশন ম্যাট্রিক্স এবং ইউনিফর্ম পূর্বে সংজ্ঞায়িত করি:
num_states = 4
initial_state_logits = tf.zeros([num_states]) # uniform distribution
daily_change_prob = 0.05
transition_probs = tf.fill([num_states, num_states],
daily_change_prob / (num_states - 1))
transition_probs = tf.linalg.set_diag(transition_probs,
tf.fill([num_states],
1 - daily_change_prob))
print("Initial state logits:\n{}".format(initial_state_logits))
print("Transition matrix:\n{}".format(transition_probs))
Initial state logits: [0. 0. 0. 0.] Transition matrix: [[0.95 0.01666667 0.01666667 0.01666667] [0.01666667 0.95 0.01666667 0.01666667] [0.01666667 0.01666667 0.95 0.01666667] [0.01666667 0.01666667 0.01666667 0.95 ]]
এর পরে, আমরা গড়ে তুলতে tfd.HiddenMarkovModel বন্টন, একটি trainable পরিবর্তনশীল ব্যবহার প্রতিটি সিস্টেমের রাষ্ট্র সঙ্গে যুক্ত হার প্রতিনিধিত্ব করতে। সেগুলি ইতিবাচক-মূল্যবান তা নিশ্চিত করতে আমরা লগ-স্পেসে হারগুলিকে প্যারামিটারাইজ করি।
# Define variable to represent the unknown log rates.
trainable_log_rates = tf.Variable(
tf.math.log(tf.reduce_mean(observed_counts)) +
tf.random.stateless_normal([num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=initial_state_logits),
transition_distribution=tfd.Categorical(probs=transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
পরিশেষে, আমরা মডেল মোট লগ ঘনত্ব নির্ধারণ, একটি স্বাস্থ্যহীন-তথ্যপূর্ণ LogNormal হারের উপর পূর্বে সহ, এবং গনা একটি অপটিমাইজার চালানোর সর্বোচ্চ আরোহী পর্যবেক্ষিত গণনা ডেটাতে (MAP) এর ফিট।
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
return (tf.reduce_sum(rate_prior.log_prob(tf.math.exp(trainable_log_rates))) +
hmm.log_prob(observed_counts))
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(learning_rate=0.1),
num_steps=100)
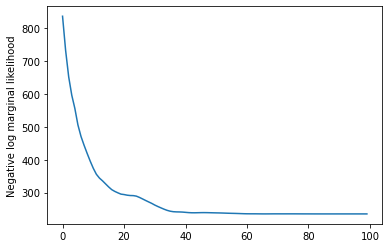
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
rates = tf.exp(trainable_log_rates)
print("Inferred rates: {}".format(rates))
print("True rates: {}".format(true_rates))
Inferred rates: [ 2.8302798 49.58499 41.928307 17.35112 ] True rates: [40, 3, 20, 50]
এটা কাজ করেছে! নোট করুন যে এই মডেলের সুপ্ত অবস্থাগুলি শুধুমাত্র স্থানান্তর পর্যন্ত শনাক্ত করা যায়, তাই আমরা যে হারগুলি পুনরুদ্ধার করেছি তা ভিন্ন ক্রমে, এবং কিছুটা গোলমাল আছে, তবে সাধারণত তারা বেশ ভাল মেলে।
রাষ্ট্রের গতিপথ পুনরুদ্ধার করা
এখন যে আমরা মডেল মাপসই করেছি, আমরা পুনর্গঠনে যা রাষ্ট্র মডেল বিশ্বাস সিস্টেম প্রতিটি timestep মুহূর্তে যে অবস্থায় ছিল চাইবেন।
এই অবর অনুমান টাস্ক হল: পর্যবেক্ষিত গন্য দেওয়া \(x_{1:T}\) এবং (হার) মডেল পরামিতি \(\lambda\), আমরা বিযুক্ত সুপ্ত ভেরিয়েবল ক্রম আবিষ্কার করতে চাই, অবর বন্টন নিম্নলিখিত \(p(z_{1:T} | x_{1:T}, \lambda)\)। একটি লুকানো মার্কভ মডেলে, আমরা মানক বার্তা-পাসিং অ্যালগরিদম ব্যবহার করে এই বিতরণের প্রান্তিক এবং অন্যান্য বৈশিষ্ট্যগুলি দক্ষতার সাথে গণনা করতে পারি। বিশেষ করে, posterior_marginals পদ্ধতি দক্ষতার (ব্যবহার গনা হবে বিচক্ষণ অনগ্রসর অ্যালগরিদম প্রান্তিক সম্ভাব্যতা বিতরণের) \(p(Z_t = z_t | x_{1:T})\) বিযুক্ত সুপ্ত রাষ্ট্র উপর \(Z_t\) প্রতিটি timestep এ \(t\)।
# Runs forward-backward algorithm to compute marginal posteriors.
posterior_dists = hmm.posterior_marginals(observed_counts)
posterior_probs = posterior_dists.probs_parameter().numpy()
পরবর্তী সম্ভাব্যতা প্লট করে, আমরা ডেটার মডেলের "ব্যাখ্যা" পুনরুদ্ধার করি: প্রতিটি রাষ্ট্র কোন সময়ে সক্রিয় থাকে?
def plot_state_posterior(ax, state_posterior_probs, title):
ln1 = ax.plot(state_posterior_probs, c='blue', lw=3, label='p(state | counts)')
ax.set_ylim(0., 1.1)
ax.set_ylabel('posterior probability')
ax2 = ax.twinx()
ln2 = ax2.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax2.set_title(title)
ax2.set_xlabel("time")
lns = ln1+ln2
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=4)
ax.grid(True, color='white')
ax2.grid(False)
fig = plt.figure(figsize=(10, 10))
plot_state_posterior(fig.add_subplot(2, 2, 1),
posterior_probs[:, 0],
title="state 0 (rate {:.2f})".format(rates[0]))
plot_state_posterior(fig.add_subplot(2, 2, 2),
posterior_probs[:, 1],
title="state 1 (rate {:.2f})".format(rates[1]))
plot_state_posterior(fig.add_subplot(2, 2, 3),
posterior_probs[:, 2],
title="state 2 (rate {:.2f})".format(rates[2]))
plot_state_posterior(fig.add_subplot(2, 2, 4),
posterior_probs[:, 3],
title="state 3 (rate {:.2f})".format(rates[3]))
plt.tight_layout()
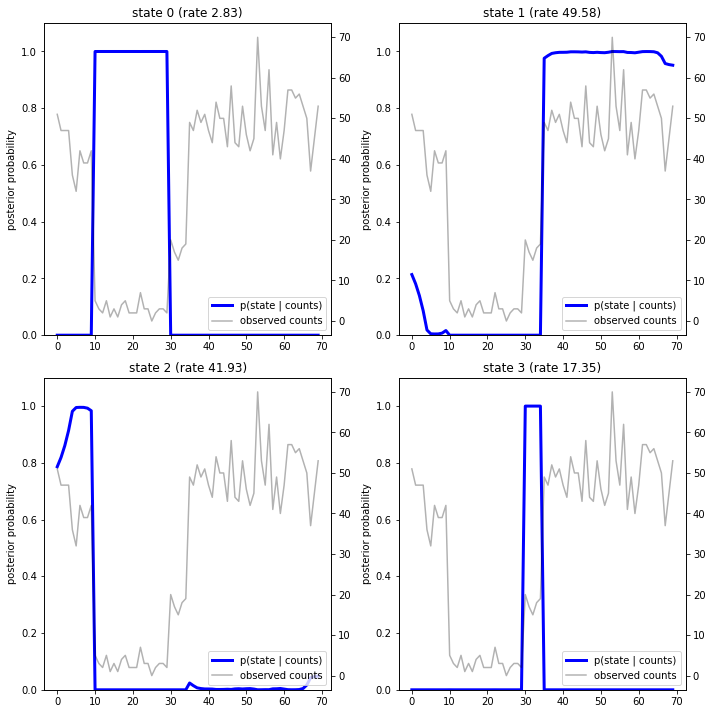
এই (সরল) ক্ষেত্রে, আমরা দেখতে পাই যে মডেলটি সাধারণত বেশ আত্মবিশ্বাসী হয়: বেশিরভাগ সময়ে এটি চারটি অবস্থার মধ্যে একটিতে সমস্ত সম্ভাব্যতা ভর করে। সৌভাগ্যবশত, ব্যাখ্যা যুক্তিসঙ্গত চেহারা!
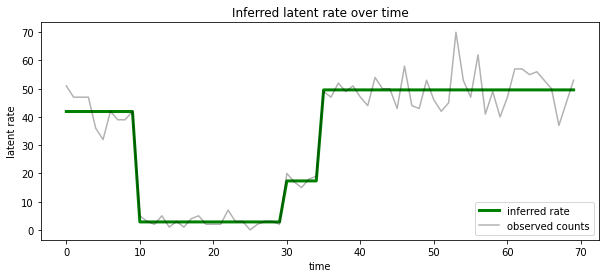
আমরা প্রতিটি timestep এ সম্ভবত সুপ্ত রাষ্ট্র সঙ্গে যুক্ত হার পরিপ্রেক্ষিতে এই অবর দৃশ্য কল্পনা করতে পারেন, একটি একক ব্যাখ্যা মধ্যে সম্ভাব্য অবর ঘনীভূত:
most_probable_states = hmm.posterior_mode(observed_counts)
most_probable_rates = tf.gather(rates, most_probable_states)
fig = plt.figure(figsize=(10, 4))
ax = fig.add_subplot(1, 1, 1)
ax.plot(most_probable_rates, c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("Inferred latent rate over time")
ax.legend(loc=4)
<matplotlib.legend.Legend at 0x7f75849e70f0>
রাজ্যের অজানা সংখ্যা
বাস্তব সমস্যায়, আমরা যে সিস্টেমে মডেলিং করছি তাতে 'সত্য' রাজ্যের সংখ্যা হয়তো আমরা জানি না। এটি সর্বদা উদ্বেগের বিষয় নাও হতে পারে: আপনি যদি বিশেষভাবে অজানা রাজ্যগুলির পরিচয় সম্পর্কে চিন্তা না করেন তবে আপনি মডেলটির প্রয়োজন হবে তা জানেন তার চেয়ে বেশি রাজ্য সহ একটি মডেল চালাতে পারেন এবং একগুচ্ছ ডুপ্লিকেট শিখতে পারেন (এর মতো কিছু) প্রকৃত রাষ্ট্রের কপি। কিন্তু ধরা যাক আপনি সুপ্ত অবস্থার 'সত্য' সংখ্যা অনুমান করার বিষয়ে যত্নশীল।
আমরা একটি মামলা হিসাবে এই দেখতে পারেন Bayesian মডেল নির্বাচন : আমরা সুপ্ত রাজ্যের একটি আলাদা নম্বর সঙ্গে প্রতিটি প্রার্থী মডেলের একটি সেট, আছে, এবং আমরা এক যে সম্ভবত পর্যবেক্ষিত তথ্য উত্পন্ন হওয়া চয়ন করতে চান। এই কাজের জন্য, আমরা একে মডেল অধীনে ডেটার প্রান্তিক সম্ভাবনা গনা (আমরা মডেল নিজেদের উপর একটি পূর্বে যোগ করতে পারিনি, কিন্তু যে এই বিশ্লেষণ প্রয়োজনীয় না; Bayesian Occam এর ক্ষুর সক্রিয় আউট সঙ্কেতাক্ষরে লিখা একটি যথেষ্ট হতে সহজ মডেলের দিকে অগ্রাধিকার)।
দুর্ভাগ্যবশত, সত্য প্রান্তিক সম্ভাবনা, যা উভয় উপর সংহত বিযুক্ত রাজ্যের \(z_{1:T}\) এবং (এর ভেক্টর) হার পরামিতি \(\lambda\), \(p(x_{1:T}) = \int p(x_{1:T}, z_{1:T}, \lambda) dz d\lambda,\) না এই মডেল জন্য নম্র হয়। সুবিধার জন্য, আমরা এটা একটি তথাকথিত "ব্যবহার আনুমানিক করব গবেষণামূলক বায়েসের " বা "টাইপ -২ সর্বাধিক সম্ভাবনা" অনুমান: তার জন্যে সম্পূর্ণরূপে (অজানা) হার পরামিতি আউট একীভূত \(\lambda\) প্রতিটি সিস্টেমের রাষ্ট্র সঙ্গে যুক্ত, আমরা নিখুত করব তাদের মান উপর:
\[\tilde{p}(x_{1:T}) = \max_\lambda \int p(x_{1:T}, z_{1:T}, \lambda) dz\]
এই আনুমানিকতা ওভারফিট হতে পারে, অর্থাৎ, এটি প্রকৃত প্রান্তিক সম্ভাবনার চেয়ে জটিল মডেল পছন্দ করবে। আমরা আরও বিশ্বস্ত অনুমান, যেমন বিবেচনা করতে পারে, নিখুঁত একটি আবদ্ধ নিম্ন ভেরিয়েশনাল, অথবা একটি মন্টে কার্লো মূল্নির্ধারক যেমন ব্যবহার annealed গুরুত্ব স্যাম্পলিং ; এগুলো (দুঃখজনকভাবে) এই নোটবুকের সুযোগের বাইরে। (Bayesian মডেল নির্বাচন এবং অনুমান, চমৎকার 7 অধ্যায় সম্পর্কে আরো জানার জন্য মেশিন লার্নিং: একটি সম্ভাব্য পরিপ্রেক্ষিত একটি ভাল রেফারেন্স।)
বস্তুত, কেবলমাত্র আমরা বিভিন্ন মান অনেক বার উপরে অপ্টিমাইজেশান rerunning দ্বারা এই মডেল তুলনা করতে পারে num_states , কিন্তু যে কাজ অনেক হতে হবে। এখানে আমরা কিভাবে সমান্তরাল একাধিক মডেল বিবেচনা, TFP এর ব্যবহার দেখাব batch_shape vectorization জন্য প্রক্রিয়া।
পরিবৃত্তি ম্যাট্রিক্স এবং প্রাথমিক অবস্থায় পূর্বে: বরং একটি একক মডেল বিবরণ নির্মাণের চেয়ে, এখন আমরা এই পরিবর্তনকে ম্যাট্রিক্স এবং পূর্বে logits, এর প্রতিটি প্রার্থী মডেল আপ জন্য এক একটি ব্যাচ নির্মাণ করব max_num_states । সহজ ব্যাচিংয়ের জন্য আমাদের নিশ্চিত করতে হবে যে সমস্ত গণনার একই 'আকৃতি' রয়েছে: এটি অবশ্যই আমাদের ফিট করা সবচেয়ে বড় মডেলের মাত্রার সাথে সামঞ্জস্যপূর্ণ হবে। ছোট মডেলগুলি পরিচালনা করার জন্য, আমরা রাষ্ট্রীয় স্থানের সর্বোচ্চ মাত্রায় তাদের বর্ণনাগুলিকে 'এম্বেড' করতে পারি, কার্যকরভাবে অবশিষ্ট মাত্রাগুলিকে ডামি স্টেট হিসাবে ব্যবহার করতে পারি যা কখনই ব্যবহৃত হয় না।
max_num_states = 10
def build_latent_state(num_states, max_num_states, daily_change_prob=0.05):
# Give probability exp(-100) ~= 0 to states outside of the current model.
active_states_mask = tf.concat([tf.ones([num_states]),
tf.zeros([max_num_states - num_states])],
axis=0)
initial_state_logits = -100. * (1 - active_states_mask)
# Build a transition matrix that transitions only within the current
# `num_states` states.
transition_probs = tf.fill([num_states, num_states],
0. if num_states == 1
else daily_change_prob / (num_states - 1))
padded_transition_probs = tf.eye(max_num_states) + tf.pad(
tf.linalg.set_diag(transition_probs,
tf.fill([num_states], - daily_change_prob)),
paddings=[(0, max_num_states - num_states),
(0, max_num_states - num_states)])
return initial_state_logits, padded_transition_probs
# For each candidate model, build the initial state prior and transition matrix.
batch_initial_state_logits = []
batch_transition_probs = []
for num_states in range(1, max_num_states+1):
initial_state_logits, transition_probs = build_latent_state(
num_states=num_states,
max_num_states=max_num_states)
batch_initial_state_logits.append(initial_state_logits)
batch_transition_probs.append(transition_probs)
batch_initial_state_logits = tf.stack(batch_initial_state_logits)
batch_transition_probs = tf.stack(batch_transition_probs)
print("Shape of initial_state_logits: {}".format(batch_initial_state_logits.shape))
print("Shape of transition probs: {}".format(batch_transition_probs.shape))
print("Example initial state logits for num_states==3:\n{}".format(batch_initial_state_logits[2, :]))
print("Example transition_probs for num_states==3:\n{}".format(batch_transition_probs[2, :, :]))
Shape of initial_state_logits: (10, 10) Shape of transition probs: (10, 10, 10) Example initial state logits for num_states==3: [ -0. -0. -0. -100. -100. -100. -100. -100. -100. -100.] Example transition_probs for num_states==3: [[0.95 0.025 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.95 0.025 0. 0. 0. 0. 0. 0. 0. ] [0.025 0.025 0.95 0. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
এখন আমরা উপরের মত একইভাবে এগিয়ে যাই। এই সময় আমরা একটি অতিরিক্ত ব্যাচ মাত্রা ব্যবহার করব trainable_rates আলাদাভাবে বিবেচনা অধীন প্রতিটি মডেল জন্য হার মাপসই।
trainable_log_rates = tf.Variable(
tf.fill([batch_initial_state_logits.shape[0], max_num_states],
tf.math.log(tf.reduce_mean(observed_counts))) +
tf.random.stateless_normal([1, max_num_states], seed=(42, 42)),
name='log_rates')
hmm = tfd.HiddenMarkovModel(
initial_distribution=tfd.Categorical(
logits=batch_initial_state_logits),
transition_distribution=tfd.Categorical(probs=batch_transition_probs),
observation_distribution=tfd.Poisson(log_rate=trainable_log_rates),
num_steps=len(observed_counts))
print("Defined HMM with batch shape: {}".format(hmm.batch_shape))
Defined HMM with batch shape: (10,)
মোট লগ প্রোব গণনা করার সময়, আমরা প্রতিটি মডেল উপাদান দ্বারা প্রকৃতপক্ষে ব্যবহৃত হারের জন্য শুধুমাত্র পূর্বের সমষ্টির জন্য সতর্ক থাকি:
rate_prior = tfd.LogNormal(5, 5)
def log_prob():
prior_lps = rate_prior.log_prob(tf.math.exp(trainable_log_rates))
prior_lp = tf.stack(
[tf.reduce_sum(prior_lps[i, :i+1]) for i in range(max_num_states)])
return prior_lp + hmm.log_prob(observed_counts)
এখন আমরা ব্যাচ উদ্দেশ্য আমরা নির্মাণ করেছি, নিখুঁত করুন, একযোগে সব প্রার্থী মডেলের ঝুলানো:
losses = tfp.math.minimize(
lambda: -log_prob(),
optimizer=tf.optimizers.Adam(0.1),
num_steps=100)
plt.plot(losses)
plt.ylabel('Negative log marginal likelihood')
Text(0, 0.5, 'Negative log marginal likelihood')
num_states = np.arange(1, max_num_states+1)
plt.plot(num_states, -losses[-1])
plt.ylim([-400, -200])
plt.ylabel("marginal likelihood $\\tilde{p}(x)$")
plt.xlabel("number of latent states")
plt.title("Model selection on latent states")
Text(0.5, 1.0, 'Model selection on latent states')
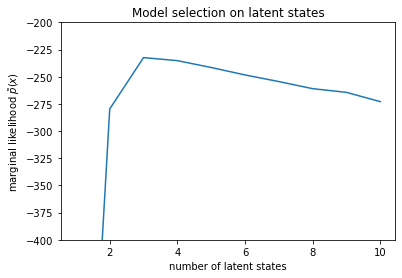
সম্ভাবনা পরীক্ষা করে, আমরা দেখতে পাই যে (আনুমানিক) প্রান্তিক সম্ভাবনা একটি তিন-রাষ্ট্র মডেল পছন্দ করে। এটি বেশ প্রশংসনীয় বলে মনে হচ্ছে -- 'সত্য' মডেলটির চারটি রাজ্য ছিল, কিন্তু কেবলমাত্র ডেটা দেখে তিন-রাষ্ট্রের ব্যাখ্যা বাতিল করা কঠিন।
আমরা প্রতিটি প্রার্থী মডেলের জন্য উপযুক্ত হারগুলিও বের করতে পারি:
rates = tf.exp(trainable_log_rates)
for i, learned_model_rates in enumerate(rates):
print("rates for {}-state model: {}".format(i+1, learned_model_rates[:i+1]))
rates for 1-state model: [32.968506] rates for 2-state model: [ 5.789209 47.948917] rates for 3-state model: [ 2.841977 48.057507 17.958897] rates for 4-state model: [ 2.8302798 49.585037 41.928406 17.351114 ] rates for 5-state model: [17.399694 77.83679 41.975216 49.62771 2.8256145] rates for 6-state model: [41.63677 77.20768 49.570934 49.557076 17.630419 2.8713436] rates for 7-state model: [41.711704 76.405945 49.581184 49.561283 17.451889 2.8722699 17.43608 ] rates for 8-state model: [41.771793 75.41323 49.568714 49.591846 17.2523 17.247969 17.231388 2.830598] rates for 9-state model: [41.83378 74.50916 49.619488 49.622494 2.8369408 17.254414 17.21532 2.5904858 17.252514 ] rates for 10-state model: [4.1886074e+01 7.3912338e+01 4.1940136e+01 4.9652588e+01 2.8485537e+00 1.7433832e+01 6.7564294e-02 1.9590002e+00 1.7430998e+01 7.8838937e-02]
এবং প্রতিটি মডেল ডেটার জন্য যে ব্যাখ্যাগুলি প্রদান করে তা প্লট করুন:
most_probable_states = hmm.posterior_mode(observed_counts)
fig = plt.figure(figsize=(14, 12))
for i, learned_model_rates in enumerate(rates):
ax = fig.add_subplot(4, 3, i+1)
ax.plot(tf.gather(learned_model_rates, most_probable_states[i]), c='green', lw=3, label='inferred rate')
ax.plot(observed_counts, c='black', alpha=0.3, label='observed counts')
ax.set_ylabel("latent rate")
ax.set_xlabel("time")
ax.set_title("{}-state model".format(i+1))
ax.legend(loc=4)
plt.tight_layout()
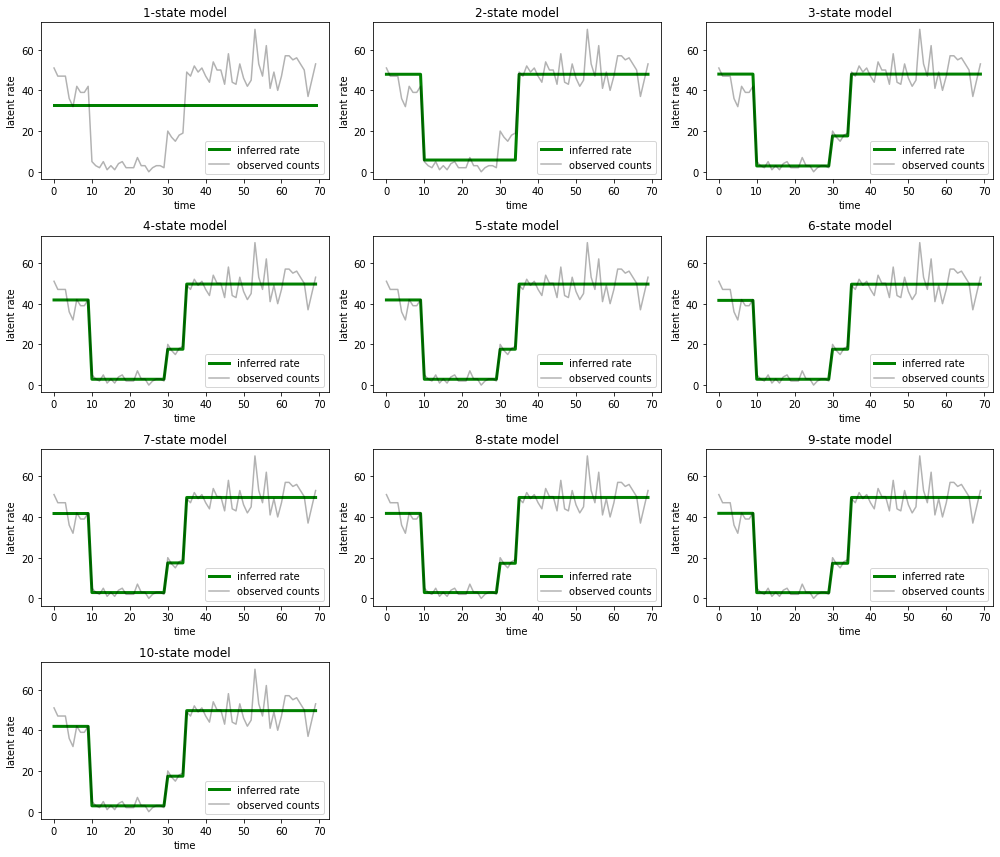
কিভাবে এক-, দুই- এবং (আরো সূক্ষ্মভাবে) তিন-রাষ্ট্র মডেল অপর্যাপ্ত ব্যাখ্যা প্রদান করে তা দেখা সহজ। মজার বিষয় হল, চারটি রাজ্যের উপরে সমস্ত মডেল মূলত একই ব্যাখ্যা প্রদান করে! এটি সম্ভবত কারণ আমাদের 'ডেটা' তুলনামূলকভাবে পরিষ্কার এবং বিকল্প ব্যাখ্যার জন্য সামান্য জায়গা ছেড়ে দেয়; অগোছালো রিয়েল-ওয়ার্ল্ড ডেটাতে আমরা আশা করব যে উচ্চ-ক্ষমতার মডেলগুলি ডেটাতে ক্রমশ আরও ভাল ফিট দেবে, কিছু ট্রেডঅফ পয়েন্ট সহ যেখানে উন্নত ফিট মডেল জটিলতার দ্বারা ছাড়িয়ে যায়।
এক্সটেনশন
এই নোটবুকের মডেলগুলিকে অনেক উপায়ে সরাসরি প্রসারিত করা যেতে পারে। উদাহরণ স্বরূপ:
- সুপ্ত অবস্থার বিভিন্ন সম্ভাবনা থাকতে দেয় (কিছু রাজ্য সাধারণ বনাম বিরল হতে পারে)
- সুপ্ত অবস্থার মধ্যে ননইউনিফর্ম ট্রানজিশনের অনুমতি দেওয়া (উদাহরণস্বরূপ, একটি মেশিন ক্র্যাশের পরে সাধারণত একটি সিস্টেম রিবুট হয় তা জানার জন্য সাধারণত ভাল পারফরম্যান্সের সময়কাল দ্বারা অনুসরণ করা হয়, ইত্যাদি)
- অন্যান্য নির্গমন মডেল, যেমন
NegativeBinomialযেমন গণনা ডেটা, বা ধারাবাহিক ডিস্ট্রিবিউশন মধ্যে dispersions নানারকম মডেলNormalরিয়েল-মূল্যবান তথ্য জন্য।
