Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
JointDistributionSequential là một phân phối giống như vừa được giới thiệu Class truyền sức mạnh cho người sử dụng nguyên mẫu nhanh mô hình Bayes. Nó cho phép bạn xâu chuỗi nhiều bản phân phối với nhau và sử dụng hàm lambda để giới thiệu các phần phụ thuộc. Điều này được thiết kế để xây dựng các mô hình Bayesian có kích thước vừa và nhỏ, bao gồm nhiều mô hình được sử dụng phổ biến như GLM, mô hình hiệu ứng hỗn hợp, mô hình hỗn hợp, v.v. Nó cho phép tất cả các tính năng cần thiết cho quy trình làm việc của Bayes: lấy mẫu dự đoán trước, Nó có thể là trình cắm thêm vào một mô hình Đồ họa Bayesian lớn hơn hoặc mạng nơ-ron. Trong Colab này, chúng tôi sẽ hiển thị một số ví dụ về cách sử dụng JointDistributionSequential để đạt được ngày này sang ngày khác workflow Bayes
Phụ thuộc & Điều kiện tiên quyết
# We will be using ArviZ, a multi-backend Bayesian diagnosis and plotting librarypip3 install -q git+git://github.com/arviz-devs/arviz.git
Nhập và thiết lập
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import arviz as az
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
Làm cho mọi thứ trở nên nhanh chóng!
Trước khi đi sâu vào, hãy đảm bảo rằng chúng tôi đang sử dụng GPU cho bản trình diễn này.
Để thực hiện việc này, hãy chọn "Thời gian chạy" -> "Thay đổi loại thời gian chạy" -> "Trình tăng tốc phần cứng" -> "GPU".
Đoạn mã sau sẽ xác minh rằng chúng tôi có quyền truy cập vào GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Phân phối chung
Lưu ý: Lớp phân phối này hữu ích khi bạn chỉ có một mô hình đơn giản. "Đơn giản" có nghĩa là đồ thị dạng chuỗi; mặc dù về mặt kỹ thuật, phương pháp này hoạt động đối với bất kỳ PGM nào có mức tối đa là 255 cho một nút (Bởi vì các hàm Python có thể có nhiều nhất là nhiều args này).
Ý tưởng cơ bản là phải có người dùng chỉ định một danh sách các callable s sản xuất tfp.Distribution trường hợp, một cho mỗi đỉnh trong họ PGM . Các callable sẽ có ít nhất là nhiều đối số như chỉ số của nó trong danh sách. (Để thuận tiện cho người dùng, các tài liệu sẽ được chuyển theo thứ tự ngược lại của quá trình tạo.) Trong nội bộ, chúng tôi sẽ "duyệt đồ thị" đơn giản bằng cách chuyển mọi giá trị của RV trước đó vào mỗi có thể gọi. Bằng cách đó, chúng tôi thực hiện [cai trị chuỗi probablity] (https://en.wikipedia.org/wiki/Chain quy tắc (xác suất% 29 # More_than_two_random_variables): \(p(\{x\}_i^d)=\prod_i^d p(x_i|x_{<i})\).
Ý tưởng này khá đơn giản, ngay cả khi là mã Python. Đây là ý chính:
# The chain rule of probability, manifest as Python code.
def log_prob(rvs, xs):
# xs[:i] is rv[i]'s markov blanket. `[::-1]` just reverses the list.
return sum(rv(*xs[i-1::-1]).log_prob(xs[i])
for i, rv in enumerate(rvs))
Bạn có thể tìm thêm thông tin từ các docstring của JointDistributionSequential , nhưng thực chất là bạn vượt qua một danh sách các bản phân phối để khởi tạo Class, nếu một số các bản phân phối trong danh sách là tùy thuộc vào sản lượng từ một phân phối thượng nguồn / biến, bạn chỉ cần quấn nó với một hàm lambda. Bây giờ chúng ta hãy xem nó hoạt động như thế nào trong hành động!
(Mạnh mẽ) Hồi quy tuyến tính
Từ PyMC3 doc GLM: Regression mạnh mẽ với outlier Detection
Lấy dữ liệu
dfhogg = pd.DataFrame(np.array([[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56]]),
columns=['id','x','y','sigma_y','sigma_x','rho_xy'])
## for convenience zero-base the 'id' and use as index
dfhogg['id'] = dfhogg['id'] - 1
dfhogg.set_index('id', inplace=True)
## standardize (mean center and divide by 1 sd)
dfhoggs = (dfhogg[['x','y']] - dfhogg[['x','y']].mean(0)) / dfhogg[['x','y']].std(0)
dfhoggs['sigma_y'] = dfhogg['sigma_y'] / dfhogg['y'].std(0)
dfhoggs['sigma_x'] = dfhogg['sigma_x'] / dfhogg['x'].std(0)
def plot_hoggs(dfhoggs):
## create xlims ylims for plotting
xlims = (dfhoggs['x'].min() - np.ptp(dfhoggs['x'])/5,
dfhoggs['x'].max() + np.ptp(dfhoggs['x'])/5)
ylims = (dfhoggs['y'].min() - np.ptp(dfhoggs['y'])/5,
dfhoggs['y'].max() + np.ptp(dfhoggs['y'])/5)
## scatterplot the standardized data
g = sns.FacetGrid(dfhoggs, size=8)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
plt.subplots_adjust(top=0.92)
_ = g.fig.suptitle('Scatterplot of Hogg 2010 dataset after standardization', fontsize=16)
return g, xlims, ylims
g = plot_hoggs(dfhoggs)
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
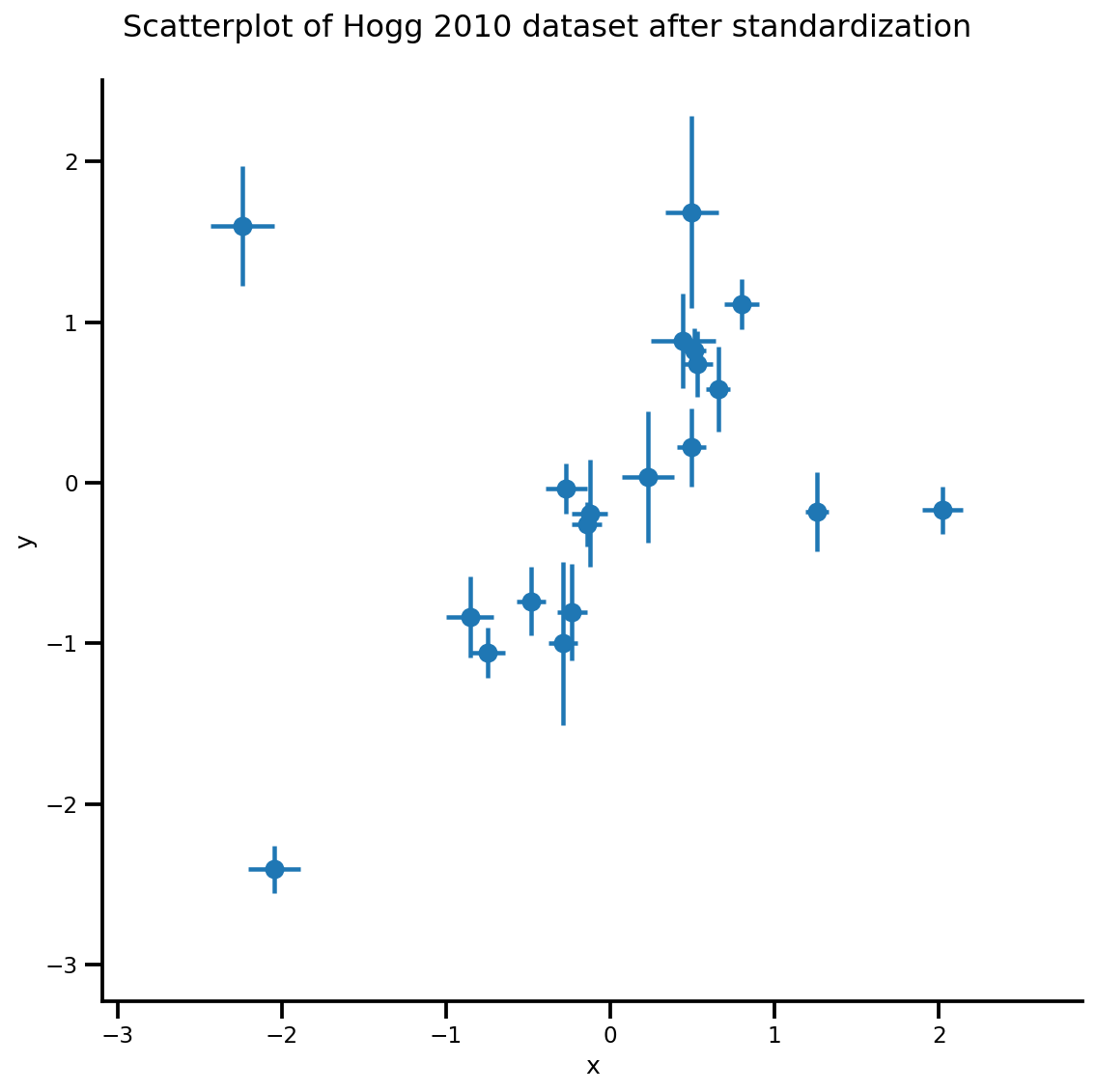
X_np = dfhoggs['x'].values
sigma_y_np = dfhoggs['sigma_y'].values
Y_np = dfhoggs['y'].values
Mô hình OLS thông thường
Bây giờ, hãy thiết lập một mô hình tuyến tính, một bài toán hồi quy hệ số chặn + đơn giản:
mdl_ols = tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# x ~ Normal(b0+b1*X, 1)
lambda b1, b0: tfd.Normal(
# Parameter transformation
loc=b0 + b1*X_np,
scale=sigma_y_np)
])
Sau đó, bạn có thể kiểm tra đồ thị của mô hình để xem sự phụ thuộc. Lưu ý rằng x được dành riêng như tên của nút cuối cùng, và bạn có thể không chắc chắn nó như là đối số lambda của bạn trong mô hình JointDistributionSequential của bạn.
mdl_ols.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Lấy mẫu từ mô hình khá đơn giản:
mdl_ols.sample()
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.50225804634794>,
<tf.Tensor: shape=(), dtype=float64, numpy=0.682740126293564>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.33051382, 0.71443618, -1.91085683, 0.89371173, -0.45060957,
-1.80448758, -0.21357082, 0.07891058, -0.20689721, -0.62690385,
-0.55225748, -0.11446535, -0.66624497, -0.86913291, -0.93605552,
-0.83965336, -0.70988597, -0.95813437, 0.15884761, -0.31113434])>]
... cung cấp danh sách tf.Tensor. Bạn có thể cắm ngay nó vào hàm log_prob để tính toán log_prob của mô hình:
prior_predictive_samples = mdl_ols.sample()
mdl_ols.log_prob(prior_predictive_samples)
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-4.97502846, -3.98544303, -4.37514505, -3.46933487, -3.80688125,
-3.42907525, -4.03263074, -3.3646366 , -4.70370938, -4.36178501,
-3.47823735, -3.94641662, -5.76906319, -4.0944128 , -4.39310708,
-4.47713894, -4.46307881, -3.98802372, -3.83027747, -4.64777082])>
Hmmm, có gì đó không đúng ở đây: chúng ta sẽ nhận được log_prob vô hướng! Trong thực tế, chúng tôi có thể tiếp tục kiểm tra để xem nếu có điều gì là tắt bằng cách gọi .log_prob_parts , mang đến cho các log_prob của mỗi nút trong mô hình đồ họa:
mdl_ols.log_prob_parts(prior_predictive_samples)
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.9699239562734849>,
<tf.Tensor: shape=(), dtype=float64, numpy=-3.459364167569284>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.54574034, 0.4438451 , 0.05414307, 0.95995326, 0.62240687,
1.00021288, 0.39665739, 1.06465152, -0.27442125, 0.06750311,
0.95105078, 0.4828715 , -1.33977506, 0.33487533, 0.03618104,
-0.04785082, -0.03379069, 0.4412644 , 0.59901066, -0.2184827 ])>]
... hóa ra nút cuối cùng không bị giảm_sum dọc theo thứ nguyên / trục iid! Do đó, khi chúng ta tính tổng, hai biến đầu tiên được phát không chính xác.
Bí quyết ở đây là sử dụng tfd.Independent để giải thích lại hình dạng batch (để phần còn lại của trục sẽ được giảm một cách chính xác):
mdl_ols_ = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
# b1 shape: (batch_shape), X shape (num_obs): we want result to have
# shape (batch_shape, num_obs)
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
])
Bây giờ, hãy kiểm tra nút / phân phối cuối cùng của mô hình, bạn có thể thấy rằng hình dạng sự kiện hiện đã được diễn giải chính xác. Lưu ý rằng nó có thể mất một chút thử và sai để có được những reinterpreted_batch_ndims đúng, nhưng bạn luôn có thể dễ dàng in phân phối hoặc tensor lấy mẫu để kiểm tra lại hình dạng!
print(mdl_ols_.sample_distributions()[0][-1])
print(mdl_ols.sample_distributions()[0][-1])
tfp.distributions.Independent("JointDistributionSequential_sample_distributions_IndependentJointDistributionSequential_sample_distributions_Normal", batch_shape=[], event_shape=[20], dtype=float64)
tfp.distributions.Normal("JointDistributionSequential_sample_distributions_Normal", batch_shape=[20], event_shape=[], dtype=float64)
prior_predictive_samples = mdl_ols_.sample()
mdl_ols_.log_prob(prior_predictive_samples) # <== Getting a scalar correctly
<tf.Tensor: shape=(), dtype=float64, numpy=-2.543425661013286>
Khác JointDistribution* API
mdl_ols_named = tfd.JointDistributionNamed(dict(
likelihood = lambda b0, b1: tfd.Independent(
tfd.Normal(
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
b0 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
b1 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
))
mdl_ols_named.log_prob(mdl_ols_named.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-5.99620966071338>
mdl_ols_named.sample() # output is a dictionary
{'b0': <tf.Tensor: shape=(), dtype=float64, numpy=0.26364058399428225>,
'b1': <tf.Tensor: shape=(), dtype=float64, numpy=-0.27209402374432207>,
'likelihood': <tf.Tensor: shape=(20,), dtype=float64, numpy=
array([ 0.6482155 , -0.39314108, 0.62744764, -0.24587987, -0.20544617,
1.01465392, -0.04705611, -0.16618702, 0.36410134, 0.3943299 ,
0.36455291, -0.27822219, -0.24423928, 0.24599518, 0.82731092,
-0.21983033, 0.56753169, 0.32830481, -0.15713064, 0.23336351])>}
Root = tfd.JointDistributionCoroutine.Root # Convenient alias.
def model():
b1 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
b0 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
yhat = b0 + b1*X_np
likelihood = yield tfd.Independent(
tfd.Normal(loc=yhat, scale=sigma_y_np),
reinterpreted_batch_ndims=1
)
mdl_ols_coroutine = tfd.JointDistributionCoroutine(model)
mdl_ols_coroutine.log_prob(mdl_ols_coroutine.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-4.566678123520463>
mdl_ols_coroutine.sample() # output is a tuple
(<tf.Tensor: shape=(), dtype=float64, numpy=0.06811002171170354>,
<tf.Tensor: shape=(), dtype=float64, numpy=-0.37477064754116807>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.91615096, -0.20244718, -0.47840159, -0.26632479, -0.60441105,
-0.48977789, -0.32422329, -0.44019322, -0.17072643, -0.20666025,
-0.55932191, -0.40801868, -0.66893181, -0.24134135, -0.50403536,
-0.51788596, -0.90071876, -0.47382338, -0.34821655, -0.38559724])>)
MLE
Và bây giờ chúng ta có thể suy luận! Bạn có thể sử dụng trình tối ưu hóa để tìm ước tính Khả năng xảy ra tối đa.
Xác định một số chức năng trợ giúp
# bfgs and lbfgs currently requries a function that returns both the value and
# gradient re the input.
import functools
def _make_val_and_grad_fn(value_fn):
@functools.wraps(value_fn)
def val_and_grad(x):
return tfp.math.value_and_gradient(value_fn, x)
return val_and_grad
# Map a list of tensors (e.g., output from JDSeq.sample([...])) to a single tensor
# modify from tfd.Blockwise
from tensorflow_probability.python.internal import dtype_util
from tensorflow_probability.python.internal import prefer_static as ps
from tensorflow_probability.python.internal import tensorshape_util
class Mapper:
"""Basically, this is a bijector without log-jacobian correction."""
def __init__(self, list_of_tensors, list_of_bijectors, event_shape):
self.dtype = dtype_util.common_dtype(
list_of_tensors, dtype_hint=tf.float32)
self.list_of_tensors = list_of_tensors
self.bijectors = list_of_bijectors
self.event_shape = event_shape
def flatten_and_concat(self, list_of_tensors):
def _reshape_map_part(part, event_shape, bijector):
part = tf.cast(bijector.inverse(part), self.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([
ps.shape(part)[:ps.size(ps.shape(part)) - ps.size(event_shape)],
[-1]
], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
list_of_tensors,
self.event_shape,
self.bijectors)
return tf.concat(tf.nest.flatten(x), axis=-1)
def split_and_reshape(self, x):
assertions = []
message = 'Input must have at least one dimension.'
if tensorshape_util.rank(x.shape) is not None:
if tensorshape_util.rank(x.shape) == 0:
raise ValueError(message)
else:
assertions.append(assert_util.assert_rank_at_least(x, 1, message=message))
with tf.control_dependencies(assertions):
splits = [
tf.cast(ps.maximum(1, ps.reduce_prod(s)), tf.int32)
for s in tf.nest.flatten(self.event_shape)
]
x = tf.nest.pack_sequence_as(
self.event_shape, tf.split(x, splits, axis=-1))
def _reshape_map_part(part, part_org, event_shape, bijector):
part = tf.cast(bijector.forward(part), part_org.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([ps.shape(part)[:-1], event_shape], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
x,
self.list_of_tensors,
self.event_shape,
self.bijectors)
return x
mapper = Mapper(mdl_ols_.sample()[:-1],
[tfb.Identity(), tfb.Identity()],
mdl_ols_.event_shape[:-1])
# mapper.split_and_reshape(mapper.flatten_and_concat(mdl_ols_.sample()[:-1]))
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input.
return -mdl_ols_.log_prob(mapper.split_and_reshape(x) + [Y_np])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=tf.zeros(2, dtype=dtype),
tolerance=1e-20,
x_tolerance=1e-8
)
b0est, b1est = lbfgs_results.position.numpy()
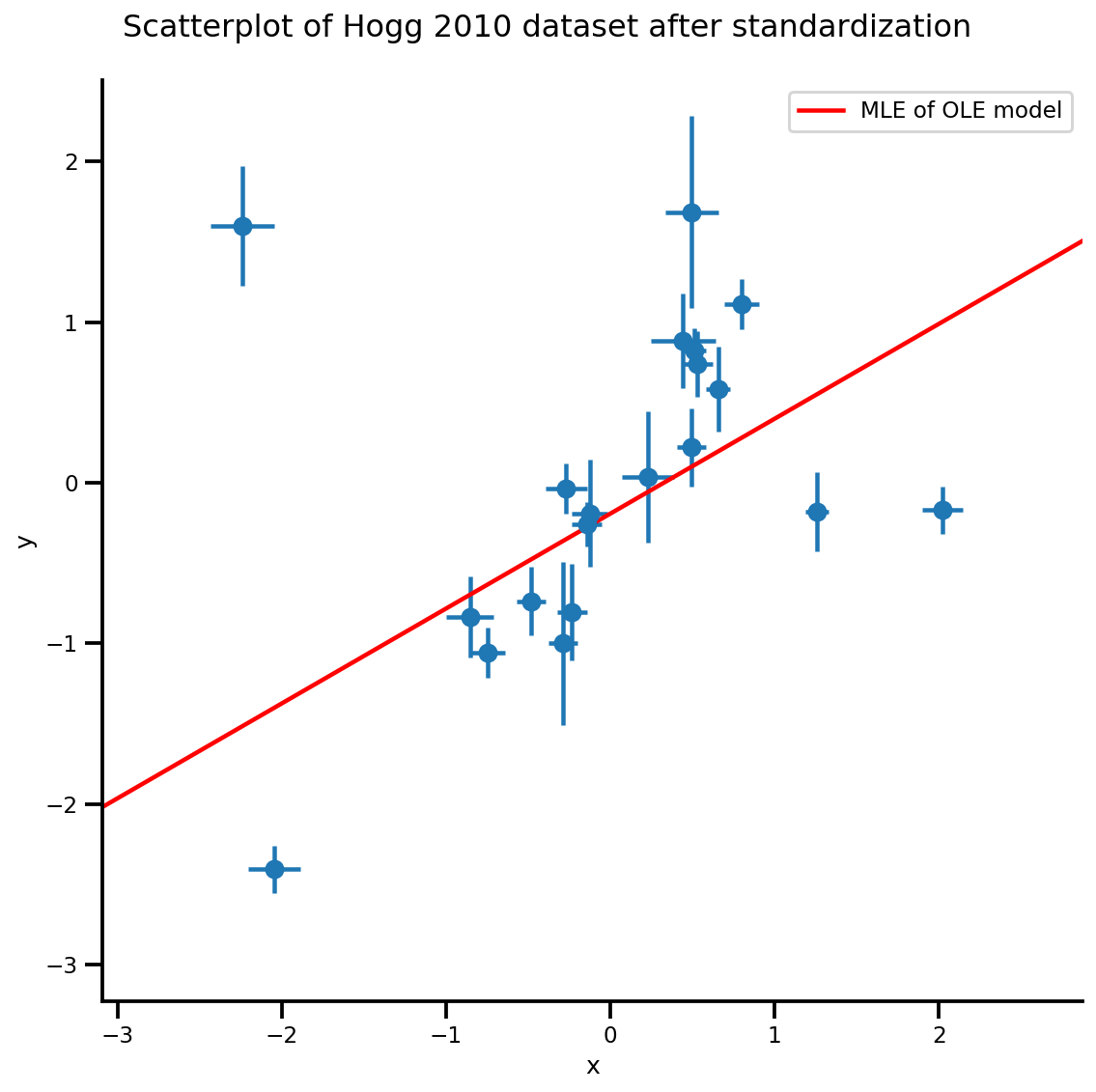
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of OLE model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
Mô hình phiên bản hàng loạt và MCMC
Trong Bayesian suy luận, chúng ta thường muốn làm việc với mẫu MCMC, như khi các mẫu được từ sau, chúng ta có thể cắm chúng vào bất kỳ chức năng để mong đợi tính toán. Tuy nhiên, MCMC API yêu cầu chúng tôi viết mô hình đó là hàng loạt thân thiện, và chúng ta có thể kiểm tra xem mô hình của chúng tôi là thực sự không phải là "batchable" bằng cách gọi sample([...])
mdl_ols_.sample(5) # <== error as some computation could not be broadcasted.
Trong trường hợp này, nó tương đối đơn giản vì chúng ta chỉ có một hàm tuyến tính bên trong mô hình của mình, việc mở rộng hình dạng sẽ thực hiện thủ thuật:
mdl_ols_batch = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0[..., tf.newaxis] + b1[..., tf.newaxis]*X_np[tf.newaxis, ...],
scale=sigma_y_np[tf.newaxis, ...]),
reinterpreted_batch_ndims=1
),
])
mdl_ols_batch.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Chúng tôi lại có thể lấy mẫu và đánh giá log_prob_parts để thực hiện một số kiểm tra:
b0, b1, y = mdl_ols_batch.sample(4)
mdl_ols_batch.log_prob_parts([b0, b1, y])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.25230168, -1.45281432, -1.87110061, -1.07665206])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.07019936, -1.59562117, -2.53387765, -1.01557632])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.45841406, 2.56829635, -4.84973951, -5.59423992])>]
Một số lưu ý bên lề:
- Chúng tôi muốn làm việc với phiên bản hàng loạt của mô hình vì đây là phiên bản nhanh nhất cho MCMC đa chuỗi. Trong trường hợp mà bạn không thể viết lại mô hình như một phiên bản đồng loạt (ví dụ, các mô hình ODE), bạn có thể lập bản đồ chức năng log_prob sử dụng
tf.map_fnđể đạt được tác dụng tương tự. - Bây giờ
mdl_ols_batch.sample()có thể không làm việc như chúng tôi có scaler trước, như chúng ta không thể làmscaler_tensor[:, None]. Giải pháp ở đây là để mở rộng tensor scaler đến bậc 1 của góitfd.Sample(..., sample_shape=1). - Một phương pháp hay là viết mô hình dưới dạng một hàm để bạn có thể thay đổi thiết lập như siêu tham số dễ dàng hơn nhiều.
def gen_ols_batch_model(X, sigma, hyperprior_mean=0, hyperprior_scale=1):
hyper_mean = tf.cast(hyperprior_mean, dtype)
hyper_scale = tf.cast(hyperprior_scale, dtype)
return tfd.JointDistributionSequential([
# b0
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# b1
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# likelihood
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0 + b1*X,
scale=sigma),
reinterpreted_batch_ndims=1
),
], validate_args=True)
mdl_ols_batch = gen_ols_batch_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
_ = mdl_ols_batch.sample()
_ = mdl_ols_batch.sample(4)
_ = mdl_ols_batch.sample([3, 4])
# Small helper function to validate log_prob shape (avoid wrong broadcasting)
def validate_log_prob_part(model, batch_shape=1, observed=-1):
samples = model.sample(batch_shape)
logp_part = list(model.log_prob_parts(samples))
# exclude observed node
logp_part.pop(observed)
for part in logp_part:
tf.assert_equal(part.shape, logp_part[-1].shape)
validate_log_prob_part(mdl_ols_batch, 4)
Kiểm tra thêm: so sánh hàm log_prob đã tạo với hàm log_prob TFP viết tay.
def ols_logp_batch(b0, b1, Y):
b0_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b0
b1_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b1
likelihood = tfd.Normal(loc=b0 + b1*X_np[None, :],
scale=sigma_y_np) # likelihood
return tf.reduce_sum(b0_prior.log_prob(b0), axis=-1) +\
tf.reduce_sum(b1_prior.log_prob(b1), axis=-1) +\
tf.reduce_sum(likelihood.log_prob(Y), axis=-1)
b0, b1, x = mdl_ols_batch.sample(4)
print(mdl_ols_batch.log_prob([b0, b1, Y_np]).numpy())
print(ols_logp_batch(b0, b1, Y_np).numpy())
[-227.37899384 -327.10043743 -570.44162789 -702.79808683] [-227.37899384 -327.10043743 -570.44162789 -702.79808683]
MCMC sử dụng Bộ lấy mẫu Không quay đầu
Một chung run_chain chức năng
@tf.function(autograph=False, experimental_compile=True)
def run_chain(init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
num_steps=500, burnin=50):
def trace_fn(_, pkr):
return (
pkr.inner_results.inner_results.target_log_prob,
pkr.inner_results.inner_results.leapfrogs_taken,
pkr.inner_results.inner_results.has_divergence,
pkr.inner_results.inner_results.energy,
pkr.inner_results.inner_results.log_accept_ratio
)
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.NoUTurnSampler(
target_log_prob_fn,
step_size=step_size),
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=burnin,
step_size_setter_fn=lambda pkr, new_step_size: pkr._replace(
inner_results=pkr.inner_results._replace(step_size=new_step_size)),
step_size_getter_fn=lambda pkr: pkr.inner_results.step_size,
log_accept_prob_getter_fn=lambda pkr: pkr.inner_results.log_accept_ratio
)
# Sampling from the chain.
chain_state, sampler_stat = tfp.mcmc.sample_chain(
num_results=num_steps,
num_burnin_steps=burnin,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
return chain_state, sampler_stat
nchain = 10
b0, b1, _ = mdl_ols_batch.sample(nchain)
init_state = [b0, b1]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1]]
target_log_prob_fn = lambda *x: mdl_ols_batch.log_prob(x + (Y_np, ))
# bijector to map contrained parameters to real
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace);
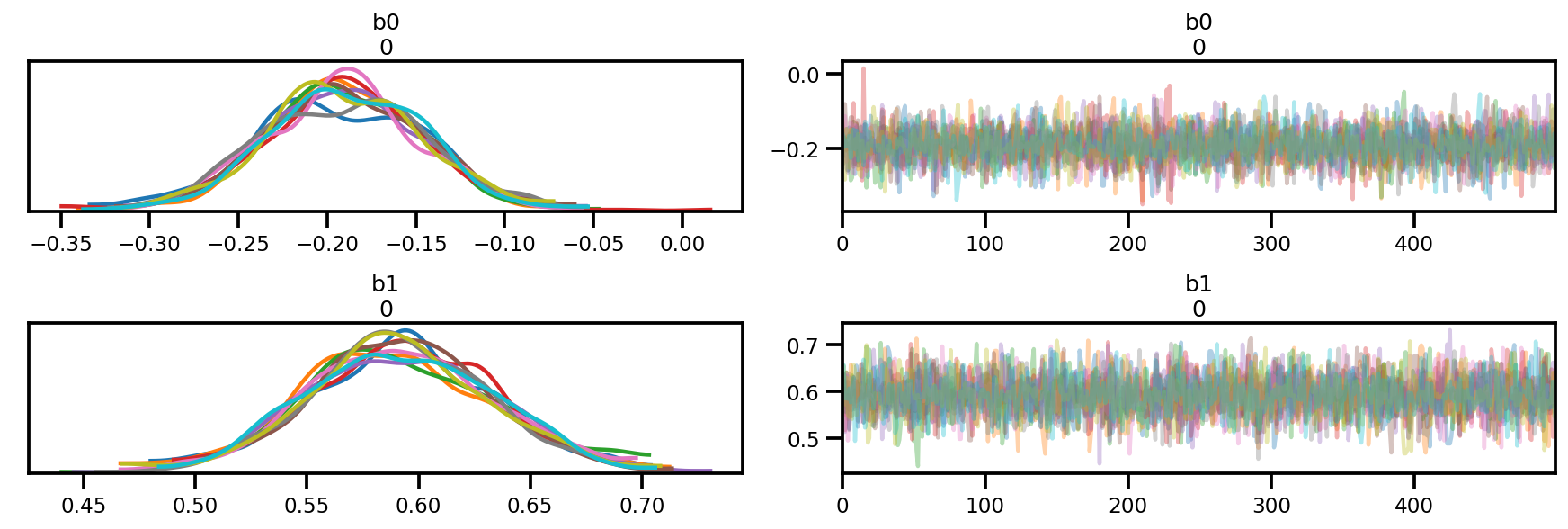
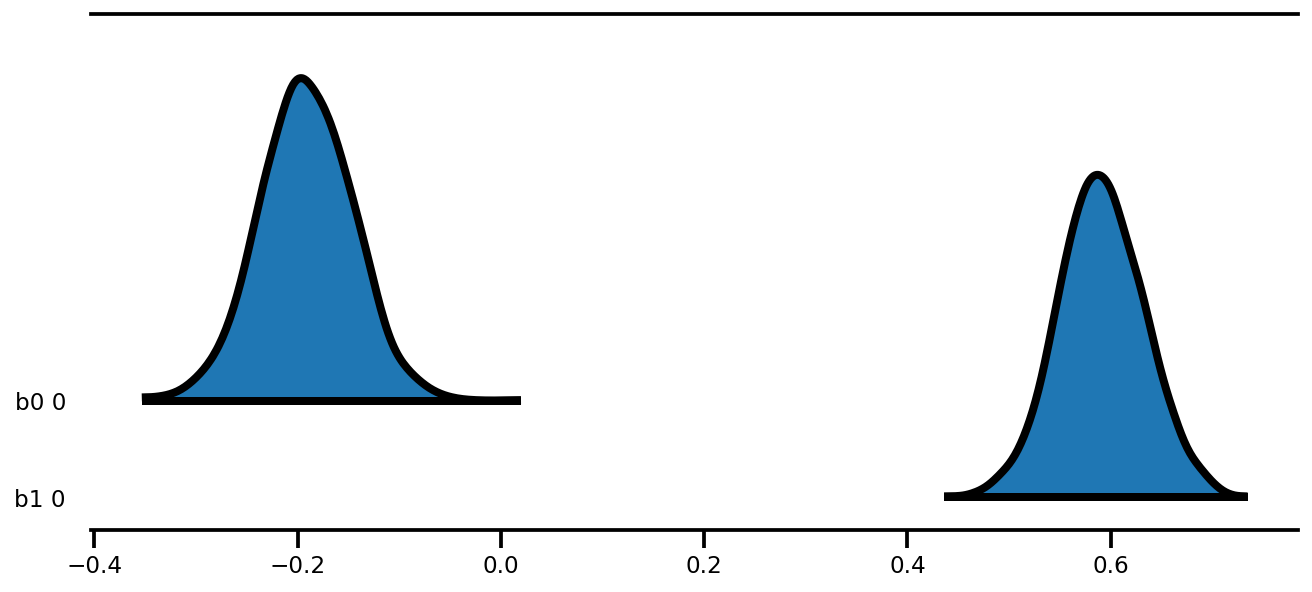
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
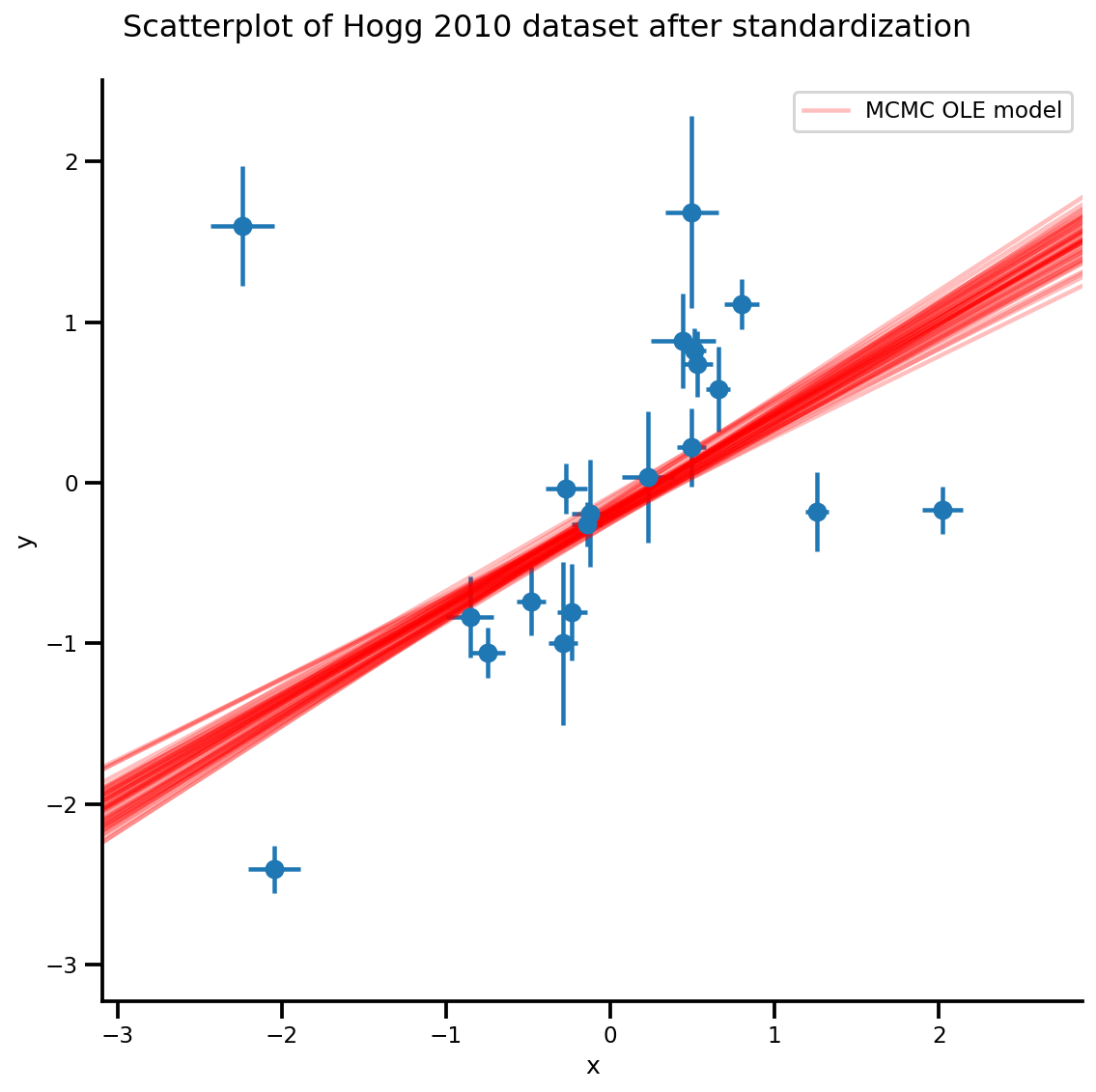
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC OLE model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Phương pháp Student-T
Lưu ý rằng kể từ bây giờ, chúng tôi luôn làm việc với phiên bản hàng loạt của một mô hình
def gen_studentt_model(X, sigma,
hyper_mean=0, hyper_scale=1, lower=1, upper=100):
loc = tf.cast(hyper_mean, dtype)
scale = tf.cast(hyper_scale, dtype)
low = tf.cast(lower, dtype)
high = tf.cast(upper, dtype)
return tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# b1 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# df ~ Uniform(a, b)
tfd.Sample(tfd.Uniform(low, high), sample_shape=1),
# likelihood ~ StudentT(df, f(b0, b1), sigma_y)
# Using Independent to ensure the log_prob is not incorrectly broadcasted.
lambda df, b1, b0: tfd.Independent(
tfd.StudentT(df=df, loc=b0 + b1*X, scale=sigma)),
], validate_args=True)
mdl_studentt = gen_studentt_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
mdl_studentt.resolve_graph()
(('b0', ()), ('b1', ()), ('df', ()), ('x', ('df', 'b1', 'b0')))
validate_log_prob_part(mdl_studentt, 4)
Chuyển tiếp mẫu (lấy mẫu dự đoán trước)
b0, b1, df, x = mdl_studentt.sample(1000)
x.shape
TensorShape([1000, 20])
MLE
# bijector to map contrained parameters to real
a, b = tf.constant(1., dtype), tf.constant(100., dtype),
# Interval transformation
tfp_interval = tfb.Inline(
inverse_fn=(
lambda x: tf.math.log(x - a) - tf.math.log(b - x)),
forward_fn=(
lambda y: (b - a) * tf.sigmoid(y) + a),
forward_log_det_jacobian_fn=(
lambda x: tf.math.log(b - a) - 2 * tf.nn.softplus(-x) - x),
forward_min_event_ndims=0,
name="interval")
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
tfp_interval,
]
mapper = Mapper(mdl_studentt.sample()[:-1],
unconstraining_bijectors,
mdl_studentt.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input, so we need to do some slicing here:
return -tf.squeeze(mdl_studentt.log_prob(
mapper.split_and_reshape(x) + [Y_np]))
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=mapper.flatten_and_concat(mdl_studentt.sample()[:-1]),
tolerance=1e-20,
x_tolerance=1e-20
)
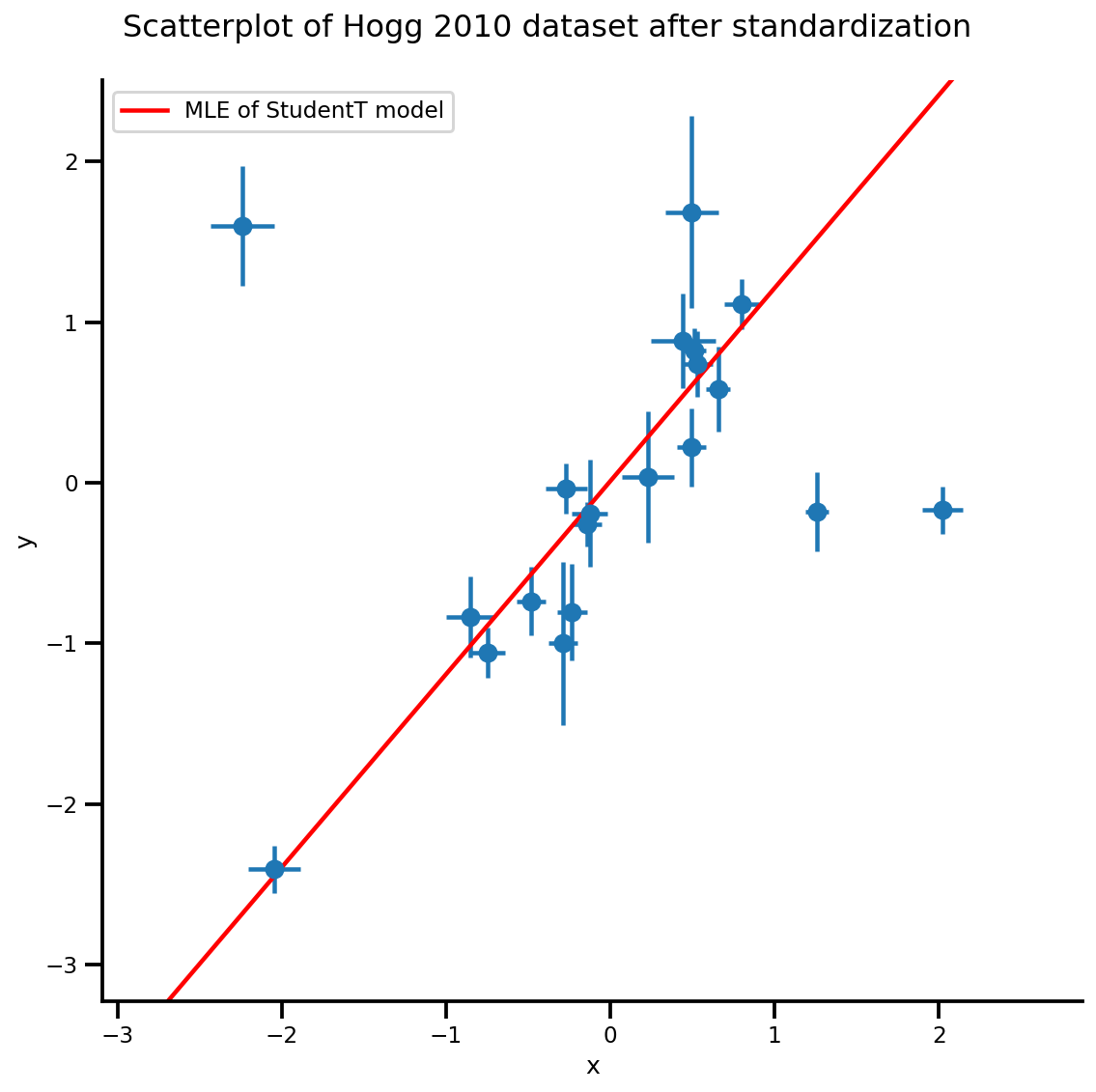
b0est, b1est, dfest = lbfgs_results.position.numpy()
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of StudentT model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
MCMC
nchain = 10
b0, b1, df, _ = mdl_studentt.sample(nchain)
init_state = [b0, b1, df]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1, .05]]
target_log_prob_fn = lambda *x: mdl_studentt.log_prob(x + (Y_np, ))
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1', 'df']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
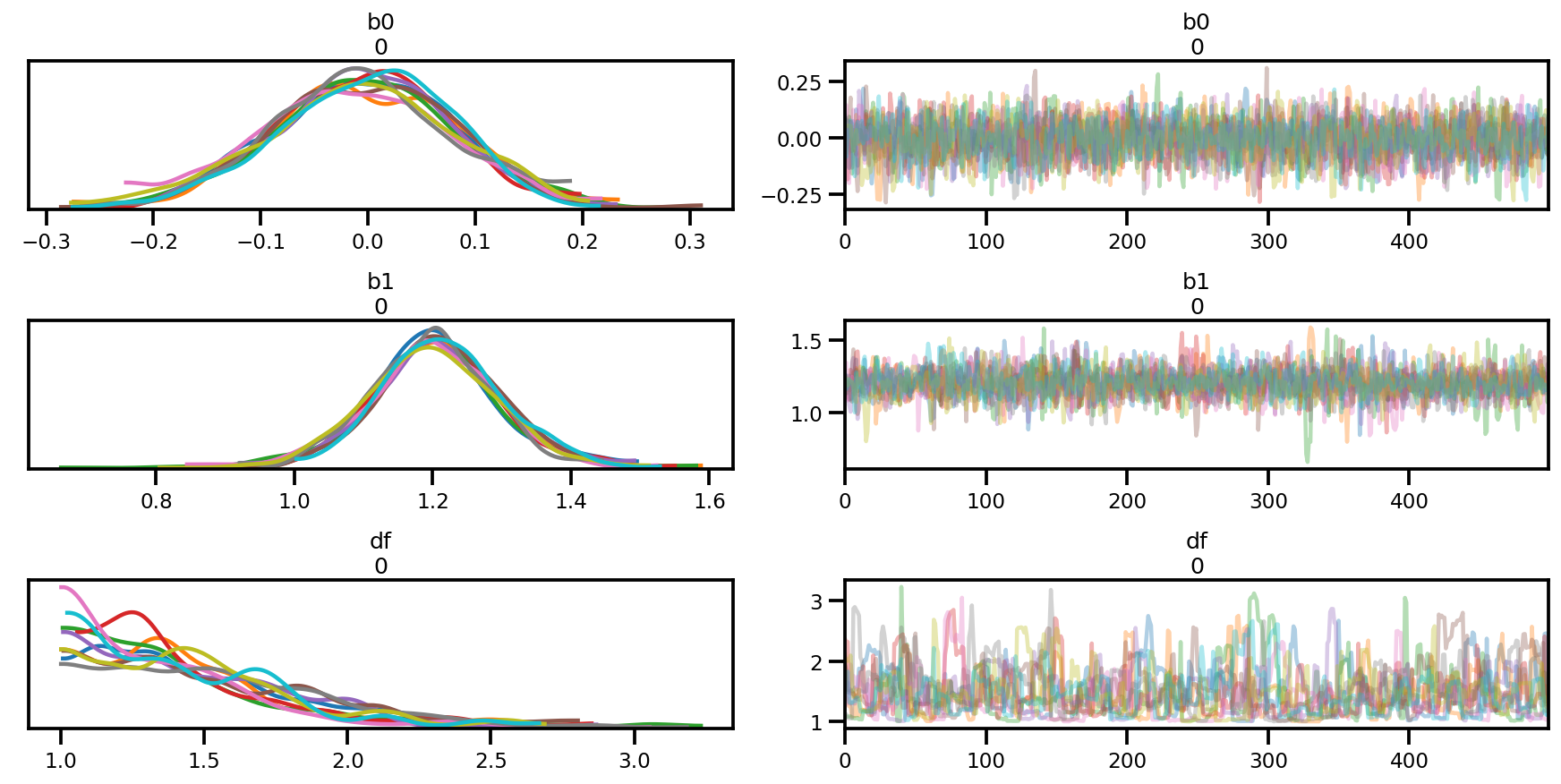
az.summary(az_trace)
az.plot_trace(az_trace);
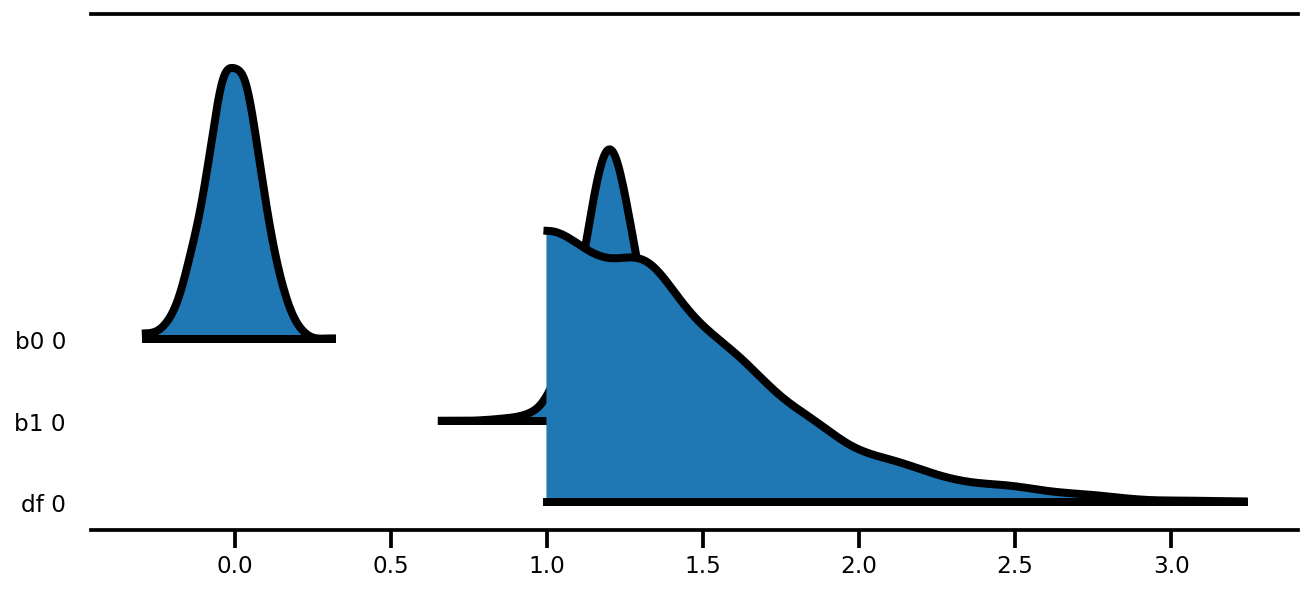
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
plt.hist(az_trace.sample_stats['tree_size'], np.linspace(.5, 25.5, 26), alpha=.5);
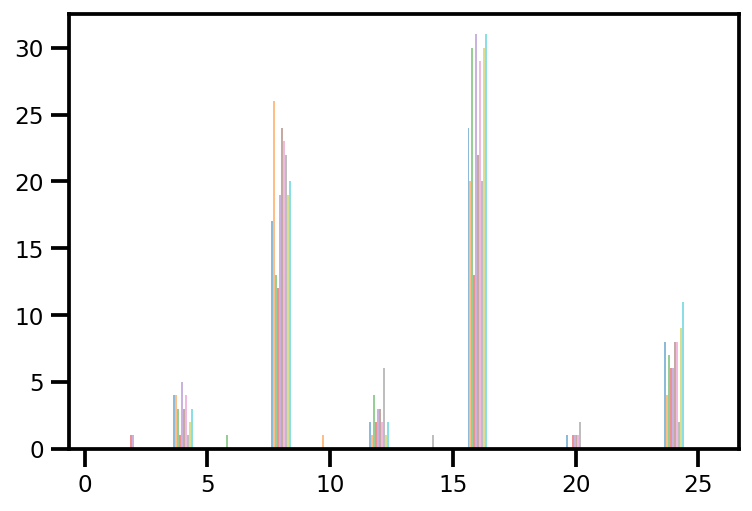
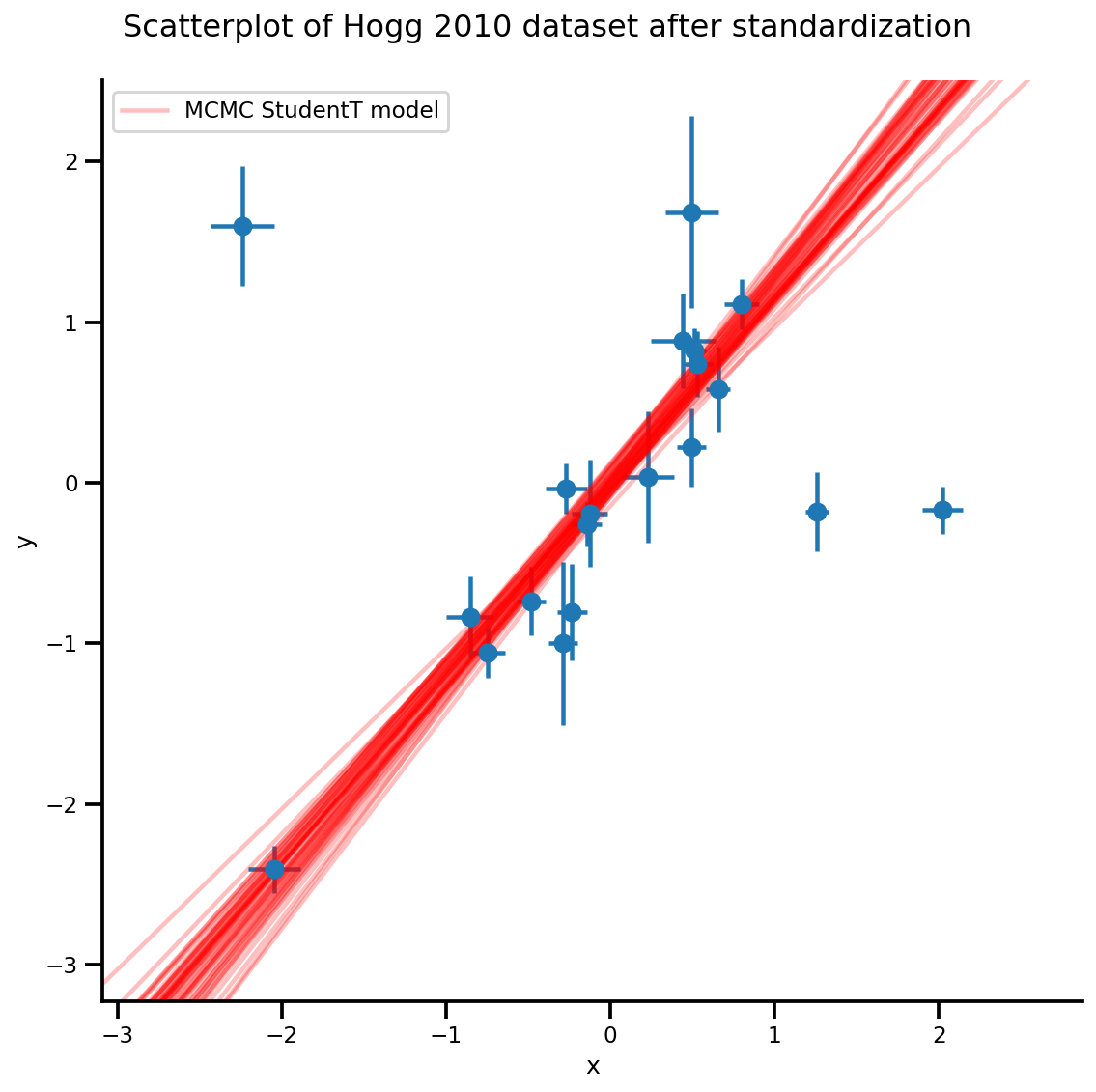
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC StudentT model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Tổng hợp một phần theo thứ bậc
Từ PyMC3 dữ liệu bóng chày cho 18 người chơi từ Efron và Morris (1975)
data = pd.read_table('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/efron-morris-75-data.tsv',
sep="\t")
at_bats, hits = data[['At-Bats', 'Hits']].values.T
n = len(at_bats)
def gen_baseball_model(at_bats, rate=1.5, a=0, b=1):
return tfd.JointDistributionSequential([
# phi
tfd.Uniform(low=tf.cast(a, dtype), high=tf.cast(b, dtype)),
# kappa_log
tfd.Exponential(rate=tf.cast(rate, dtype)),
# thetas
lambda kappa_log, phi: tfd.Sample(
tfd.Beta(
concentration1=tf.exp(kappa_log)*phi,
concentration0=tf.exp(kappa_log)*(1.0-phi)),
sample_shape=n
),
# likelihood
lambda thetas: tfd.Independent(
tfd.Binomial(
total_count=tf.cast(at_bats, dtype),
probs=thetas
)),
])
mdl_baseball = gen_baseball_model(at_bats)
mdl_baseball.resolve_graph()
(('phi', ()),
('kappa_log', ()),
('thetas', ('kappa_log', 'phi')),
('x', ('thetas',)))
Chuyển tiếp mẫu (lấy mẫu dự đoán trước)
phi, kappa_log, thetas, y = mdl_baseball.sample(4)
# phi, kappa_log, thetas, y
Một lần nữa, hãy lưu ý rằng nếu bạn không sử dụng Independent, bạn sẽ kết thúc với log_prob có sai batch_shape.
# check logp
pprint(mdl_baseball.log_prob_parts([phi, kappa_log, thetas, hits]))
print(mdl_baseball.log_prob([phi, kappa_log, thetas, hits]))
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([0., 0., 0., 0.])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.1721297 , -0.95946498, -0.72591188, 0.23993813])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([59.35192283, 7.0650634 , 0.83744911, 74.14370935])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3279.75191016, -931.10438484, -512.59197688, -1131.08043597])>] tf.Tensor([-3220.22785762 -924.99878641 -512.48043966 -1056.69678849], shape=(4,), dtype=float64)
MLE
Một tính năng khá tuyệt vời của tfp.optimizer là, bạn có thể tối ưu hóa song song với k lô điểm bắt đầu và chỉ định stopping_condition kwarg: bạn có thể thiết lập nó để tfp.optimizer.converged_all để xem nếu tất cả họ đều tìm thấy cùng tối thiểu, hoặc tfp.optimizer.converged_any tìm một giải pháp địa phương nhanh chóng.
unconstraining_bijectors = [
tfb.Sigmoid(),
tfb.Exp(),
tfb.Sigmoid(),
]
phi, kappa_log, thetas, y = mdl_baseball.sample(10)
mapper = Mapper([phi, kappa_log, thetas],
unconstraining_bijectors,
mdl_baseball.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
return -mdl_baseball.log_prob(mapper.split_and_reshape(x) + [hits])
start = mapper.flatten_and_concat([phi, kappa_log, thetas])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
num_correction_pairs=10,
initial_position=start,
# lbfgs actually can work in batch as well
stopping_condition=tfp.optimizer.converged_any,
tolerance=1e-50,
x_tolerance=1e-50,
parallel_iterations=10,
max_iterations=200
)
lbfgs_results.converged.numpy(), lbfgs_results.failed.numpy()
(array([False, False, False, False, False, False, False, False, False,
False]),
array([ True, True, True, True, True, True, True, True, True,
True]))
result = lbfgs_results.position[lbfgs_results.converged & ~lbfgs_results.failed]
result
<tf.Tensor: shape=(0, 20), dtype=float64, numpy=array([], shape=(0, 20), dtype=float64)>
LBFGS đã không hội tụ.
if result.shape[0] > 0:
phi_est, kappa_est, theta_est = mapper.split_and_reshape(result)
phi_est, kappa_est, theta_est
MCMC
target_log_prob_fn = lambda *x: mdl_baseball.log_prob(x + (hits, ))
nchain = 4
phi, kappa_log, thetas, _ = mdl_baseball.sample(nchain)
init_state = [phi, kappa_log, thetas]
step_size=[tf.cast(i, dtype=dtype) for i in [.1, .1, .1]]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
burnin=200)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['phi', 'kappa_log', 'thetas']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace, compact=True);
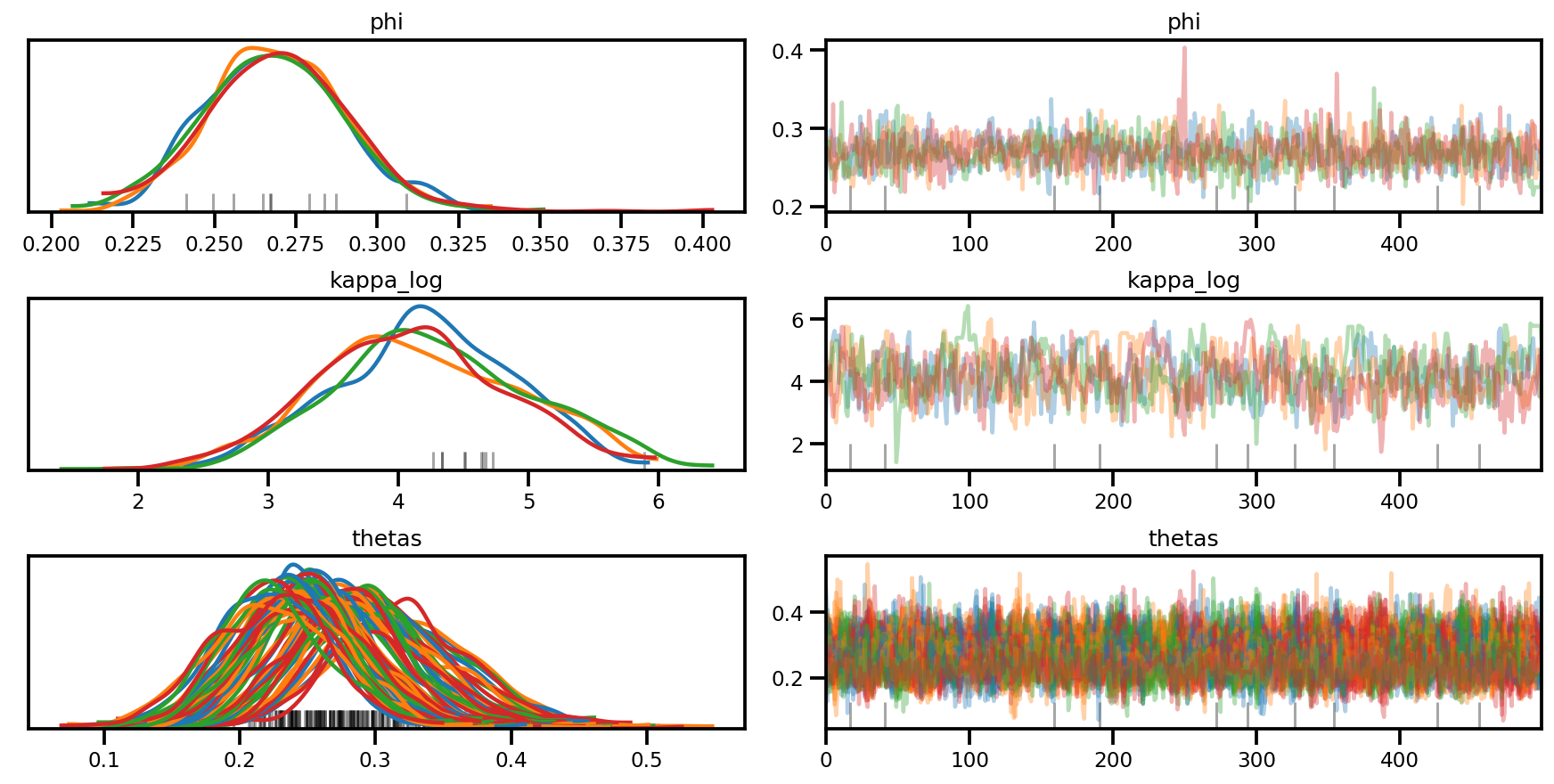
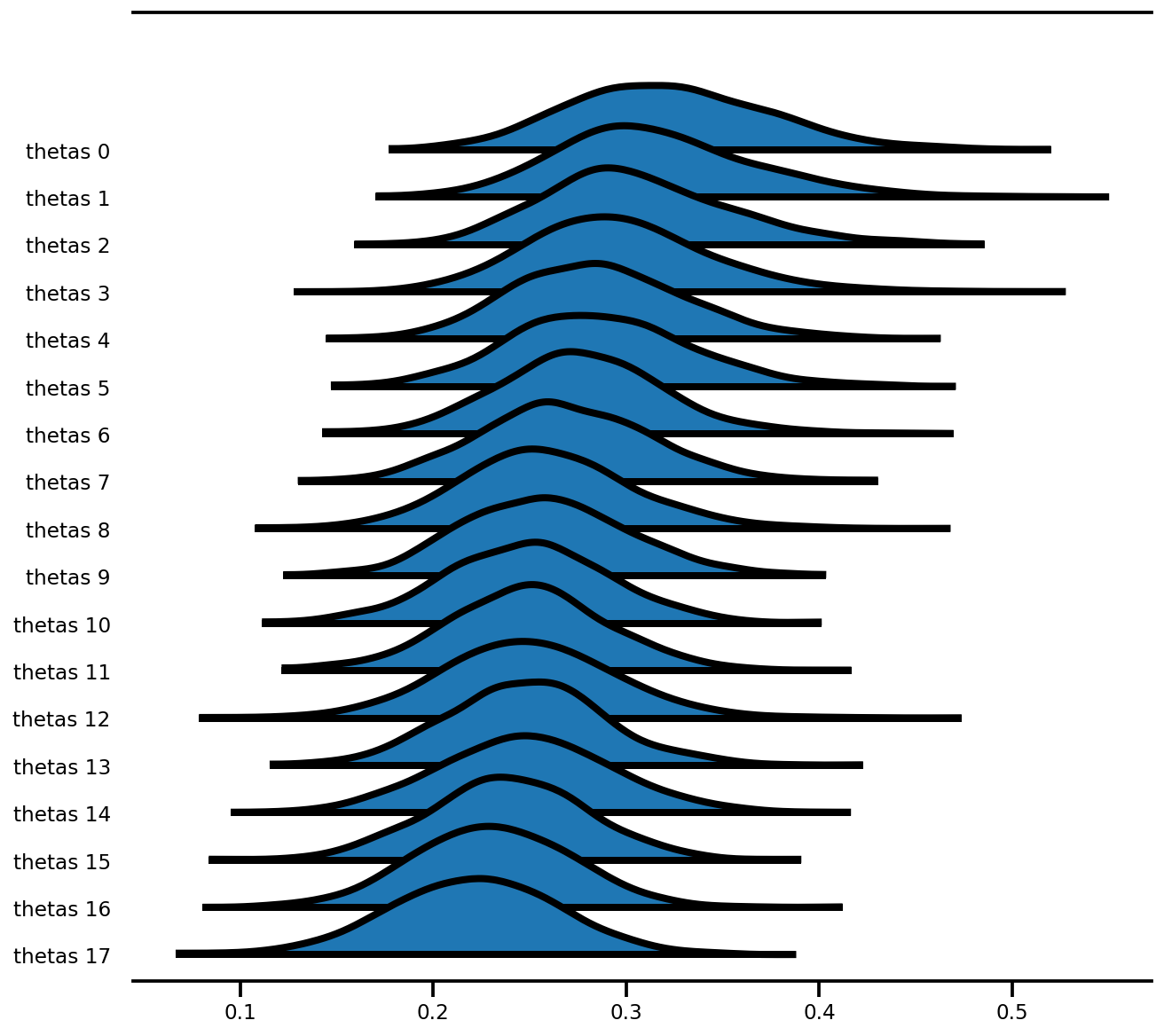
az.plot_forest(az_trace,
var_names=['thetas'],
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 8));
Mô hình hiệu ứng hỗn hợp (Radon)
Mô hình cuối cùng trong doc PyMC3: Một Primer về phương pháp Bayes cho đa cấp Modeling
Một số thay đổi trước đó (quy mô nhỏ hơn, v.v.)
Tải dữ liệu thô và dọn dẹp
srrs2 = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/srrs2.dat')
srrs2.columns = srrs2.columns.map(str.strip)
srrs_mn = srrs2[srrs2.state=='MN'].copy()
srrs_mn['fips'] = srrs_mn.stfips*1000 + srrs_mn.cntyfips
cty = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/cty.dat')
cty_mn = cty[cty.st=='MN'].copy()
cty_mn[ 'fips'] = 1000*cty_mn.stfips + cty_mn.ctfips
srrs_mn = srrs_mn.merge(cty_mn[['fips', 'Uppm']], on='fips')
srrs_mn = srrs_mn.drop_duplicates(subset='idnum')
u = np.log(srrs_mn.Uppm)
n = len(srrs_mn)
srrs_mn.county = srrs_mn.county.map(str.strip)
mn_counties = srrs_mn.county.unique()
counties = len(mn_counties)
county_lookup = dict(zip(mn_counties, range(len(mn_counties))))
county = srrs_mn['county_code'] = srrs_mn.county.replace(county_lookup).values
radon = srrs_mn.activity
srrs_mn['log_radon'] = log_radon = np.log(radon + 0.1).values
floor_measure = srrs_mn.floor.values.astype('float')
# Create new variable for mean of floor across counties
xbar = srrs_mn.groupby('county')['floor'].mean().rename(county_lookup).values
Đối với các mô hình có sự chuyển đổi phức tạp, việc triển khai nó theo kiểu chức năng sẽ giúp việc viết và thử nghiệm dễ dàng hơn nhiều. Ngoài ra, nó làm cho chức năng log_prob tạo theo chương trình có điều kiện dựa trên (lô nhỏ) dữ liệu đã nhập dễ dàng hơn nhiều:
def affine(u_val, x_county, county, floor, gamma, eps, b):
"""Linear equation of the coefficients and the covariates, with broadcasting."""
return (tf.transpose((gamma[..., 0]
+ gamma[..., 1]*u_val[:, None]
+ gamma[..., 2]*x_county[:, None]))
+ tf.gather(eps, county, axis=-1)
+ b*floor)
def gen_radon_model(u_val, x_county, county, floor,
mu0=tf.zeros([], dtype, name='mu0')):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
# sigma_a
tfd.HalfCauchy(loc=mu0, scale=5.),
# eps
lambda sigma_a: tfd.Sample(
tfd.Normal(loc=mu0, scale=sigma_a), sample_shape=counties),
# gamma
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=3),
# b
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=1),
# sigma_y
tfd.Sample(tfd.HalfCauchy(loc=mu0, scale=5.), sample_shape=1),
# likelihood
lambda sigma_y, b, gamma, eps: tfd.Independent(
tfd.Normal(
loc=affine(u_val, x_county, county, floor, gamma, eps, b),
scale=sigma_y
),
reinterpreted_batch_ndims=1
),
])
contextual_effect2 = gen_radon_model(
u.values, xbar[county], county, floor_measure)
@tf.function(autograph=False)
def unnormalized_posterior_log_prob(sigma_a, gamma, eps, b, sigma_y):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return contextual_effect2.log_prob(
[sigma_a, gamma, eps, b, sigma_y, log_radon])
assert [4] == unnormalized_posterior_log_prob(
*contextual_effect2.sample(4)[:-1]).shape
samples = contextual_effect2.sample(4)
pprint([s.shape for s in samples])
[TensorShape([4]), TensorShape([4, 85]), TensorShape([4, 3]), TensorShape([4, 1]), TensorShape([4, 1]), TensorShape([4, 919])]
contextual_effect2.log_prob_parts(list(samples)[:-1] + [log_radon])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3.95681828, -2.45693443, -2.53310078, -4.7717536 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-340.65975204, -217.11139018, -246.50498667, -369.79687704])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-20.49822449, -20.38052557, -18.63843525, -17.83096972])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-5.94765605, -5.91460848, -6.66169402, -5.53894593])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-2.10293999, -4.34186631, -2.10744955, -3.016717 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=
array([-29022322.1413861 , -114422.36893361, -8708500.81752865,
-35061.92497235])>]
Suy luận biến đổi
Một tính năng rất mạnh mẽ của JointDistribution* là bạn có thể tạo ra một xấp xỉ dễ dàng cho VI. Ví dụ, để làm meanfield ADVI, bạn chỉ cần kiểm tra biểu đồ và thay thế tất cả các phân phối không quan sát được bằng một phân phối Chuẩn.
Meanfield ADVI
Bạn cũng có thể sử dụng tính năng experimential trong tensorflow_probability / python / thử nghiệm / vi để xây dựng xấp xỉ biến phân, trong đó chủ yếu là cùng một logic sử dụng dưới đây (ví dụ, sử dụng JointDistribution để xây dựng xấp xỉ), nhưng với sản lượng xấp xỉ trong không gian ban đầu thay vì không gian không giới hạn.
from tensorflow_probability.python.mcmc.transformed_kernel import (
make_transform_fn, make_transformed_log_prob)
# Wrap logp so that all parameters are in the Real domain
# copied and edited from tensorflow_probability/python/mcmc/transformed_kernel.py
unconstraining_bijectors = [
tfb.Exp(),
tfb.Identity(),
tfb.Identity(),
tfb.Identity(),
tfb.Exp()
]
unnormalized_log_prob = lambda *x: contextual_effect2.log_prob(x + (log_radon,))
contextual_effect_posterior = make_transformed_log_prob(
unnormalized_log_prob,
unconstraining_bijectors,
direction='forward',
# TODO(b/72831017): Disable caching until gradient linkage
# generally works.
enable_bijector_caching=False)
# debug
if True:
# Check the two versions of log_prob - they should be different given the Jacobian
rv_samples = contextual_effect2.sample(4)
_inverse_transform = make_transform_fn(unconstraining_bijectors, 'inverse')
_forward_transform = make_transform_fn(unconstraining_bijectors, 'forward')
pprint([
unnormalized_log_prob(*rv_samples[:-1]),
contextual_effect_posterior(*_inverse_transform(rv_samples[:-1])),
unnormalized_log_prob(
*_forward_transform(
tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1])
),
contextual_effect_posterior(
*[tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1]]
),
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73354969e+04, -5.51622488e+04, -2.77754609e+08, -1.09065161e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73331358e+04, -5.51582029e+04, -2.77754602e+08, -1.09065134e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>]
# Build meanfield ADVI for a jointdistribution
# Inspect the input jointdistribution and replace the list of distribution with
# a list of Normal distribution, each with the same shape.
def build_meanfield_advi(jd_list, observed_node=-1):
"""
The inputted jointdistribution needs to be a batch version
"""
# Sample to get a list of Tensors
list_of_values = jd_list.sample(1) # <== sample([]) might not work
# Remove the observed node
list_of_values.pop(observed_node)
# Iterate the list of Tensor to a build a list of Normal distribution (i.e.,
# the Variational posterior)
distlist = []
for i, value in enumerate(list_of_values):
dtype = value.dtype
rv_shape = value[0].shape
loc = tf.Variable(
tf.random.normal(rv_shape, dtype=dtype),
name='meanfield_%s_mu' % i,
dtype=dtype)
scale = tfp.util.TransformedVariable(
tf.fill(rv_shape, value=tf.constant(0.02, dtype)),
tfb.Softplus(),
name='meanfield_%s_scale' % i,
)
approx_node = tfd.Normal(loc=loc, scale=scale)
if loc.shape == ():
distlist.append(approx_node)
else:
distlist.append(
# TODO: make the reinterpreted_batch_ndims more flexible (for
# minibatch etc)
tfd.Independent(approx_node, reinterpreted_batch_ndims=1)
)
# pass list to JointDistribution to initiate the meanfield advi
meanfield_advi = tfd.JointDistributionSequential(distlist)
return meanfield_advi
advi = build_meanfield_advi(contextual_effect2, observed_node=-1)
# Check the logp and logq
advi_samples = advi.sample(4)
pprint([
advi.log_prob(advi_samples),
contextual_effect_posterior(*advi_samples)
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([231.26836839, 229.40755095, 227.10287879, 224.05914594])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-10615.93542431, -11743.21420129, -10376.26732337, -11338.00600103])>]
opt = tf.optimizers.Adam(learning_rate=.1)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior,
surrogate_posterior=advi,
optimizer=opt,
sample_size=10,
num_steps=300)
return loss_
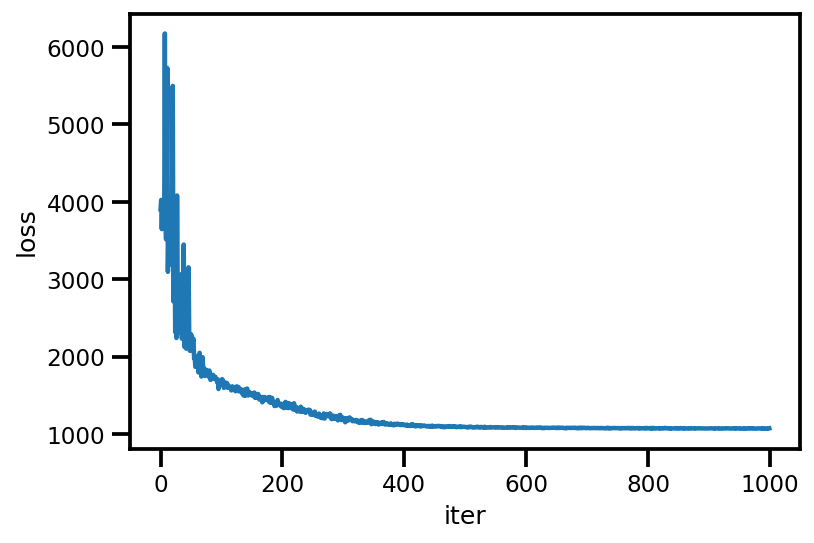
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
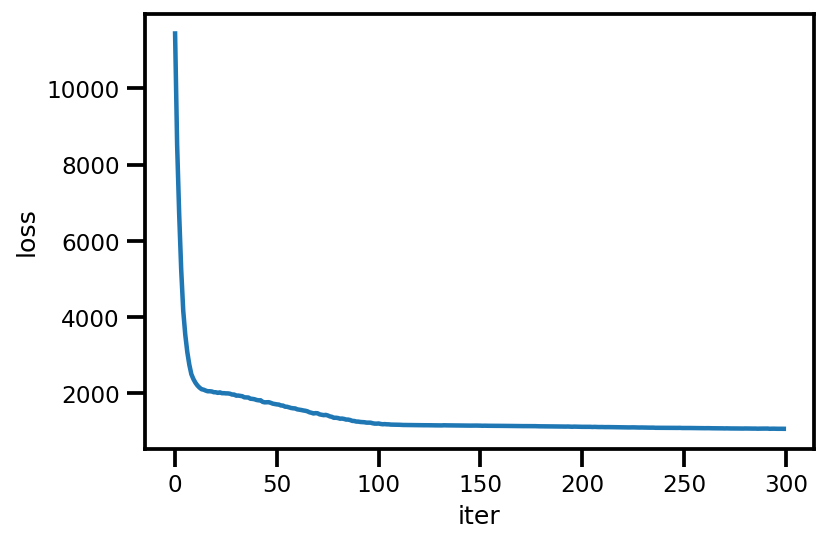
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param = advi.trainable_variables
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param[i*2].numpy(),
"sd": free_param[i*2+1].numpy()}
approx_param.keys()
dict_keys(['sigma_a', 'eps', 'gamma', 'b', 'sigma_y'])
approx_param['gamma']
{'mu': array([1.28145814, 0.70365287, 1.02689857]),
'sd': array([-3.6604972 , -2.68153218, -2.04176524])}
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
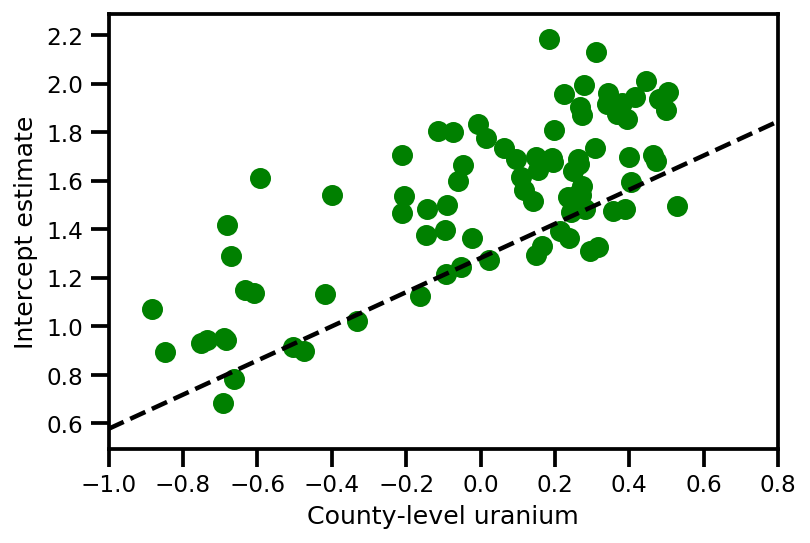
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
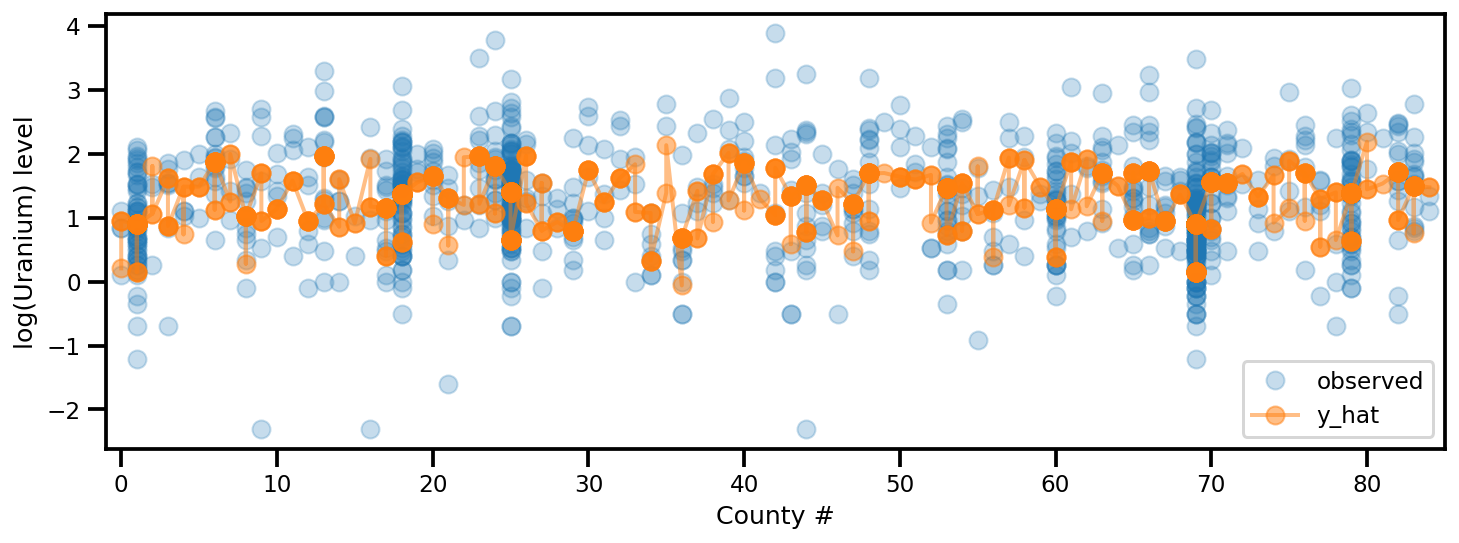
FullRank ADVI
Đối với ADVI xếp hạng đầy đủ, chúng tôi muốn ước lượng hạng sau bằng Gaussian đa biến.
USE_FULLRANK = True
*prior_tensors, _ = contextual_effect2.sample()
mapper = Mapper(prior_tensors,
[tfb.Identity() for _ in prior_tensors],
contextual_effect2.event_shape[:-1])
rv_shape = ps.shape(mapper.flatten_and_concat(mapper.list_of_tensors))
init_val = tf.random.normal(rv_shape, dtype=dtype)
loc = tf.Variable(init_val, name='loc', dtype=dtype)
if USE_FULLRANK:
# cov_param = tfp.util.TransformedVariable(
# 10. * tf.eye(rv_shape[0], dtype=dtype),
# tfb.FillScaleTriL(),
# name='cov_param'
# )
FillScaleTriL = tfb.FillScaleTriL(
diag_bijector=tfb.Chain([
tfb.Shift(tf.cast(.01, dtype)),
tfb.Softplus(),
tfb.Shift(tf.cast(np.log(np.expm1(1.)), dtype))]),
diag_shift=None)
cov_param = tfp.util.TransformedVariable(
.02 * tf.eye(rv_shape[0], dtype=dtype),
FillScaleTriL,
name='cov_param')
advi_approx = tfd.MultivariateNormalTriL(
loc=loc, scale_tril=cov_param)
else:
# An alternative way to build meanfield ADVI.
cov_param = tfp.util.TransformedVariable(
.02 * tf.ones(rv_shape, dtype=dtype),
tfb.Softplus(),
name='cov_param'
)
advi_approx = tfd.MultivariateNormalDiag(
loc=loc, scale_diag=cov_param)
contextual_effect_posterior2 = lambda x: contextual_effect_posterior(
*mapper.split_and_reshape(x)
)
# Check the logp and logq
advi_samples = advi_approx.sample(7)
pprint([
advi_approx.log_prob(advi_samples),
contextual_effect_posterior2(advi_samples)
])
[<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([238.81841799, 217.71022639, 234.57207103, 230.0643819 ,
243.73140943, 226.80149702, 232.85184209])>,
<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([-3638.93663169, -3664.25879314, -3577.69371677, -3696.25705312,
-3689.12130489, -3777.53698383, -3659.4982734 ])>]
learning_rate = tf.optimizers.schedules.ExponentialDecay(
initial_learning_rate=1e-2,
decay_steps=10,
decay_rate=0.99,
staircase=True)
opt = tf.optimizers.Adam(learning_rate=learning_rate)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior2,
surrogate_posterior=advi_approx,
optimizer=opt,
sample_size=10,
num_steps=1000)
return loss_
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
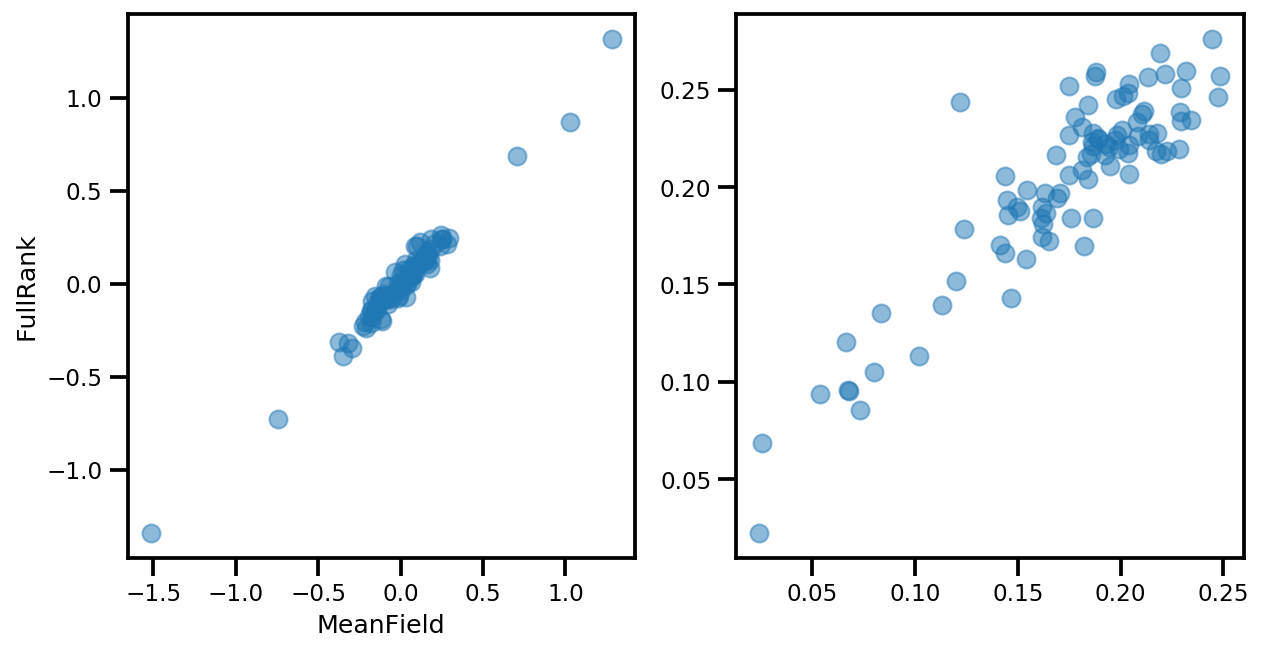
# debug
if True:
_, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(mapper.flatten_and_concat(advi.mean()), advi_approx.mean(), 'o', alpha=.5)
ax[1].plot(mapper.flatten_and_concat(advi.stddev()), advi_approx.stddev(), 'o', alpha=.5)
ax[0].set_xlabel('MeanField')
ax[0].set_ylabel('FullRank')
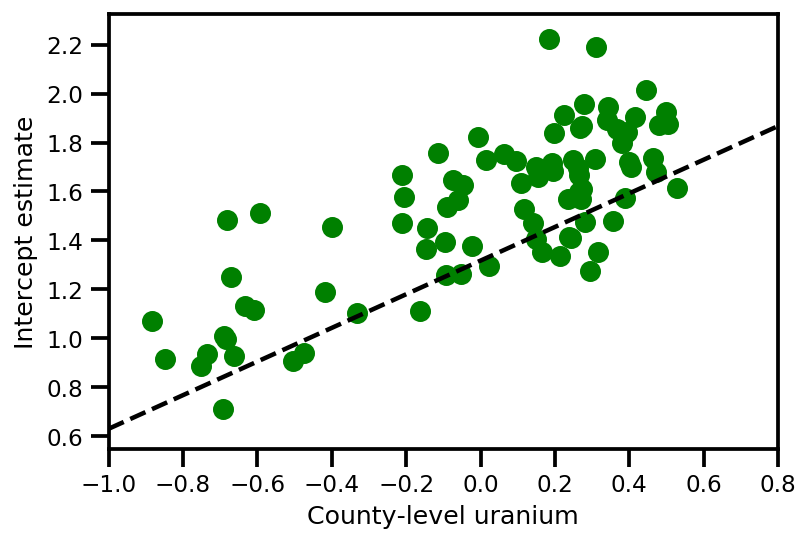
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param_mean = mapper.split_and_reshape(advi_approx.mean())
free_param_std = mapper.split_and_reshape(advi_approx.stddev())
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param_mean[i].numpy(),
"cov_info": free_param_std[i].numpy()}
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
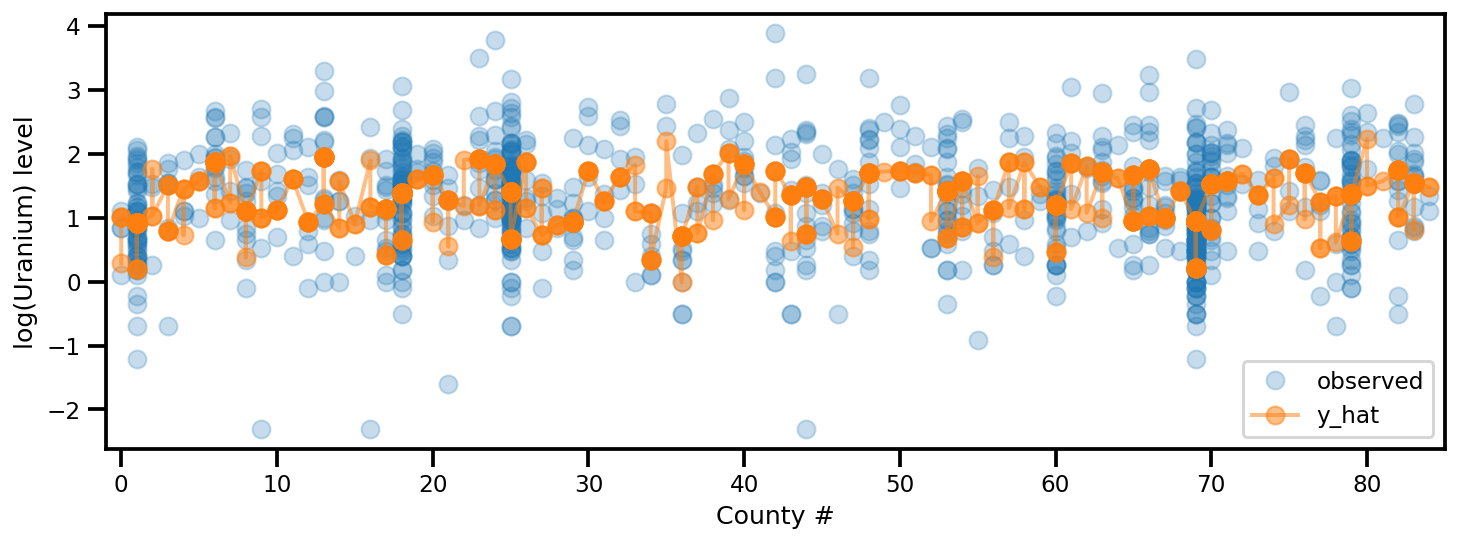
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
Mô hình hỗn hợp Beta-Bernoulli
Mô hình hỗn hợp trong đó nhiều người đánh giá gắn nhãn một số mặt hàng, với các nhãn tiềm ẩn (đúng) không xác định.
dtype = tf.float32
n = 50000 # number of examples reviewed
p_bad_ = 0.1 # fraction of bad events
m = 5 # number of reviewers for each example
rcl_ = .35 + np.random.rand(m)/10
prc_ = .65 + np.random.rand(m)/10
# PARAMETER TRANSFORMATION
tpr = rcl_
fpr = p_bad_*tpr*(1./prc_-1.)/(1.-p_bad_)
tnr = 1 - fpr
# broadcast to m reviewer.
batch_prob = np.asarray([tpr, fpr]).T
mixture = tfd.Mixture(
tfd.Categorical(
probs=[p_bad_, 1-p_bad_]),
[
tfd.Independent(tfd.Bernoulli(probs=tpr), 1),
tfd.Independent(tfd.Bernoulli(probs=fpr), 1),
])
# Generate reviewer response
X_tf = mixture.sample([n])
# run once to always use the same array as input
# so we can compare the estimation from different
# inference method.
X_np = X_tf.numpy()
# batched Mixture model
mdl_mixture = tfd.JointDistributionSequential([
tfd.Sample(tfd.Beta(5., 2.), m),
tfd.Sample(tfd.Beta(2., 2.), m),
tfd.Sample(tfd.Beta(1., 10), 1),
lambda p_bad, rcl, prc: tfd.Sample(
tfd.Mixture(
tfd.Categorical(
probs=tf.concat([p_bad, 1.-p_bad], -1)),
[
tfd.Independent(tfd.Bernoulli(
probs=rcl), 1),
tfd.Independent(tfd.Bernoulli(
probs=p_bad*rcl*(1./prc-1.)/(1.-p_bad)), 1)
]
), (n, )),
])
mdl_mixture.resolve_graph()
(('prc', ()), ('rcl', ()), ('p_bad', ()), ('x', ('p_bad', 'rcl', 'prc')))
prc, rcl, p_bad, x = mdl_mixture.sample(4)
x.shape
TensorShape([4, 50000, 5])
mdl_mixture.log_prob_parts([prc, rcl, p_bad, X_np[np.newaxis, ...]])
[<tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.4828572, 2.957961 , 2.9355168, 2.6116824], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.14646745, 1.3308513 , 1.1205603 , 0.5441705 ], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.3733709, 1.8020535, 2.1865845, 1.5701319], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-54326.664, -52683.93 , -64407.67 , -55007.895], dtype=float32)>]
Suy luận (NUTS)
nchain = 10
prc, rcl, p_bad, _ = mdl_mixture.sample(nchain)
initial_chain_state = [prc, rcl, p_bad]
# Since MCMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
unconstraining_bijectors = [
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
]
step_size = [tf.cast(i, dtype=dtype) for i in [1e-3, 1e-3, 1e-3]]
X_expanded = X_np[np.newaxis, ...]
target_log_prob_fn = lambda *x: mdl_mixture.log_prob(x + (X_expanded, ))
samples, sampler_stat = run_chain(
initial_chain_state, step_size, target_log_prob_fn,
unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
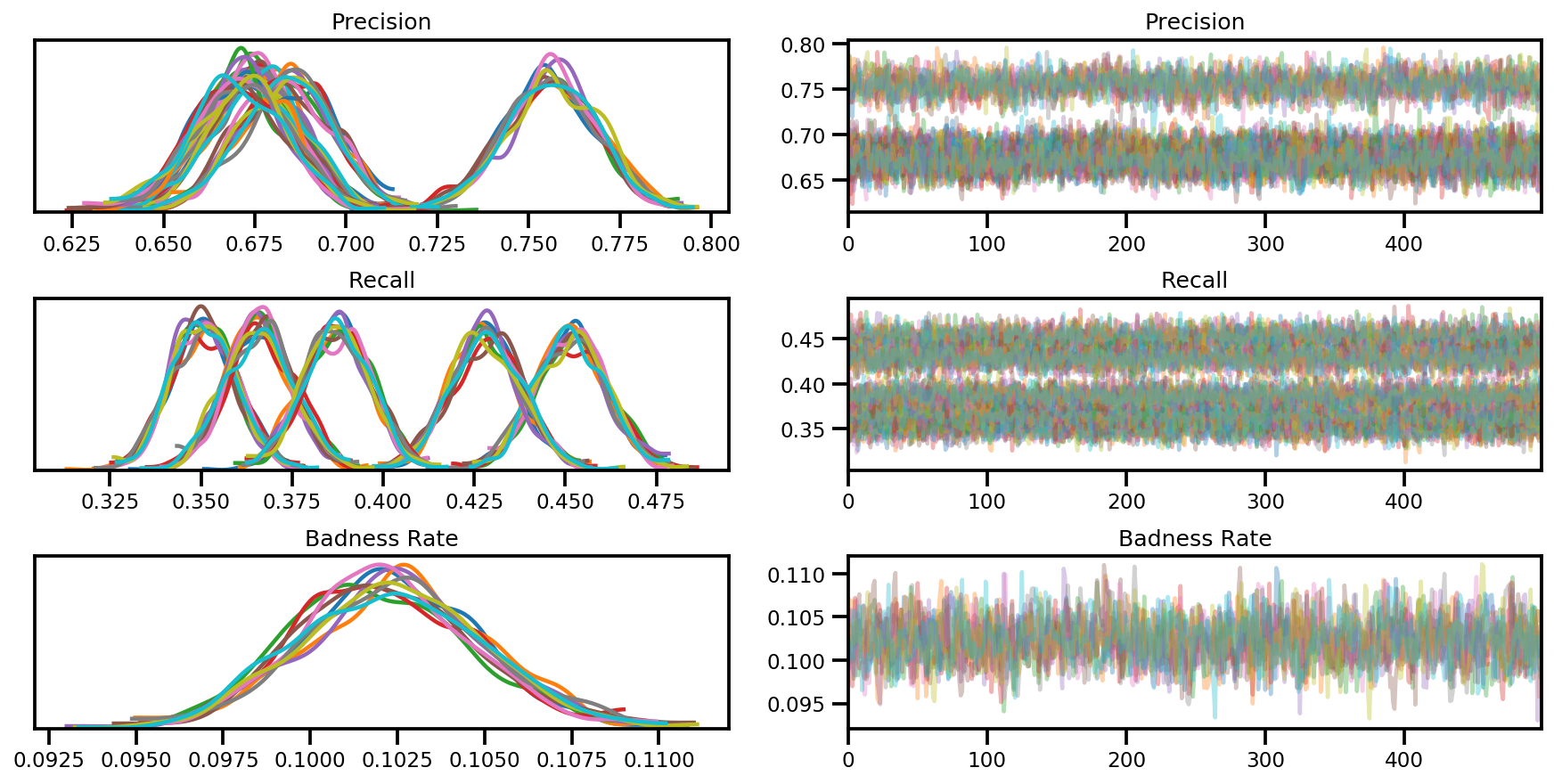
var_name = ['Precision', 'Recall', 'Badness Rate']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
axes = az.plot_trace(az_trace, compact=True);