Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
JointDistributionSequential est une distribution semblable à la classe nouvellement introduite , qui permet aux utilisateurs de modèle bayésien prototype rapide. Il vous permet d'enchaîner plusieurs distributions et d'utiliser la fonction lambda pour introduire des dépendances. Ceci est conçu pour créer des modèles bayésiens de petite à moyenne taille, y compris de nombreux modèles couramment utilisés comme les GLM, les modèles à effets mixtes, les modèles de mélange, etc. Il permet toutes les fonctionnalités nécessaires à un flux de travail bayésien : échantillonnage prédictif préalable, il peut être connecté à un autre modèle graphique bayésien ou réseau de neurones plus grand. Dans ce Colab, nous montrerons quelques exemples de la façon d'utiliser JointDistributionSequential pour atteindre votre jour à l'autre flux de travail bayésienne
Dépendances et prérequis
# We will be using ArviZ, a multi-backend Bayesian diagnosis and plotting librarypip3 install -q git+git://github.com/arviz-devs/arviz.git
Importer et configurer
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import arviz as az
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
Faites les choses rapidement !
Avant de plonger, assurons-nous que nous utilisons un GPU pour cette démo.
Pour ce faire, sélectionnez "Runtime" -> "Modifier le type d'exécution" -> "Accélérateur matériel" -> "GPU".
L'extrait suivant vérifiera que nous avons accès à un GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Distribution conjointe
Remarques : Cette classe de distribution est utile lorsque vous n'avez qu'un modèle simple. « Simple » signifie des graphiques en forme de chaîne ; bien que l'approche fonctionne techniquement pour n'importe quel PGM avec un degré d'au plus 255 pour un seul nœud (parce que les fonctions Python peuvent avoir au plus autant d'arguments).
L'idée de base est d'avoir l'utilisateur de spécifier une liste de callable s qui produisent tfp.Distribution cas, un pour chaque sommet dans leur PGM . Le callable aura au plus autant d'arguments que son index dans la liste. (Pour la commodité de l'utilisateur, les arguments seront passés dans l'ordre inverse de la création.) En interne, nous "parcourrons le graphique" simplement en passant la valeur de chaque RV précédente dans chaque appelable. Ce faisant , nous mettons en œuvre la [règle de la chaîne de probablity] (https://en.wikipedia.org/wiki/Chain règle (probabilité de 29% # More_than_two_random_variables): \(p(\{x\}_i^d)=\prod_i^d p(x_i|x_{<i})\).
L'idée est assez simple, même en code Python. Voici l'essentiel :
# The chain rule of probability, manifest as Python code.
def log_prob(rvs, xs):
# xs[:i] is rv[i]'s markov blanket. `[::-1]` just reverses the list.
return sum(rv(*xs[i-1::-1]).log_prob(xs[i])
for i, rv in enumerate(rvs))
Vous pouvez trouver plus d' informations de la docstring de JointDistributionSequential , mais l'essentiel est que vous passez une liste des distributions pour initialiser la classe, si certaines distributions dans la liste dépend de la sortie d' une autre distribution / variables en amont, vous enveloppez juste avec un fonction lambda. Voyons maintenant comment cela fonctionne en action !
(Robuste) Régression linéaire
De PyMC3 doc GLM: régression robuste avec le cas particulier de détection
Obtenir des données
dfhogg = pd.DataFrame(np.array([[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56]]),
columns=['id','x','y','sigma_y','sigma_x','rho_xy'])
## for convenience zero-base the 'id' and use as index
dfhogg['id'] = dfhogg['id'] - 1
dfhogg.set_index('id', inplace=True)
## standardize (mean center and divide by 1 sd)
dfhoggs = (dfhogg[['x','y']] - dfhogg[['x','y']].mean(0)) / dfhogg[['x','y']].std(0)
dfhoggs['sigma_y'] = dfhogg['sigma_y'] / dfhogg['y'].std(0)
dfhoggs['sigma_x'] = dfhogg['sigma_x'] / dfhogg['x'].std(0)
def plot_hoggs(dfhoggs):
## create xlims ylims for plotting
xlims = (dfhoggs['x'].min() - np.ptp(dfhoggs['x'])/5,
dfhoggs['x'].max() + np.ptp(dfhoggs['x'])/5)
ylims = (dfhoggs['y'].min() - np.ptp(dfhoggs['y'])/5,
dfhoggs['y'].max() + np.ptp(dfhoggs['y'])/5)
## scatterplot the standardized data
g = sns.FacetGrid(dfhoggs, size=8)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
plt.subplots_adjust(top=0.92)
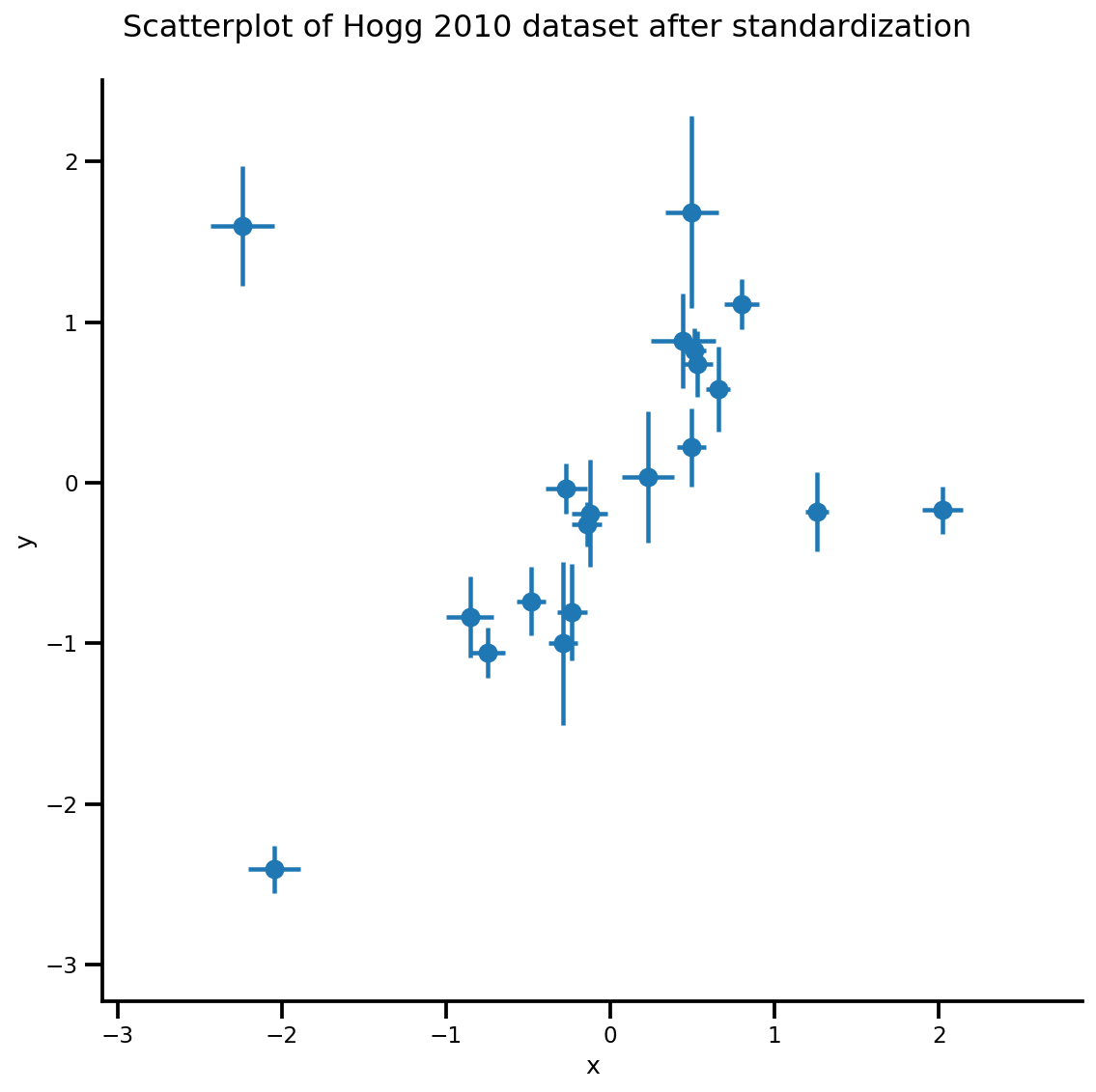
_ = g.fig.suptitle('Scatterplot of Hogg 2010 dataset after standardization', fontsize=16)
return g, xlims, ylims
g = plot_hoggs(dfhoggs)
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
X_np = dfhoggs['x'].values
sigma_y_np = dfhoggs['sigma_y'].values
Y_np = dfhoggs['y'].values
Modèle OLS conventionnel
Maintenant, mettons en place un modèle linéaire, un simple problème de régression d'interception + pente :
mdl_ols = tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# x ~ Normal(b0+b1*X, 1)
lambda b1, b0: tfd.Normal(
# Parameter transformation
loc=b0 + b1*X_np,
scale=sigma_y_np)
])
Vous pouvez ensuite consulter le graphique du modèle pour voir la dépendance. Notez que x est réservé comme le nom du dernier noeud, et vous ne pouvez pas vous comme votre argument lambda dans votre modèle JointDistributionSequential.
mdl_ols.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
L'échantillonnage à partir du modèle est assez simple :
mdl_ols.sample()
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.50225804634794>,
<tf.Tensor: shape=(), dtype=float64, numpy=0.682740126293564>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.33051382, 0.71443618, -1.91085683, 0.89371173, -0.45060957,
-1.80448758, -0.21357082, 0.07891058, -0.20689721, -0.62690385,
-0.55225748, -0.11446535, -0.66624497, -0.86913291, -0.93605552,
-0.83965336, -0.70988597, -0.95813437, 0.15884761, -0.31113434])>]
... qui donne une liste de tf.Tensor. Vous pouvez immédiatement le brancher sur la fonction log_prob pour calculer le log_prob du modèle :
prior_predictive_samples = mdl_ols.sample()
mdl_ols.log_prob(prior_predictive_samples)
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-4.97502846, -3.98544303, -4.37514505, -3.46933487, -3.80688125,
-3.42907525, -4.03263074, -3.3646366 , -4.70370938, -4.36178501,
-3.47823735, -3.94641662, -5.76906319, -4.0944128 , -4.39310708,
-4.47713894, -4.46307881, -3.98802372, -3.83027747, -4.64777082])>
Hmmm, quelque chose ne va pas ici : nous devrions obtenir un log_prob scalaire ! En fait, nous pouvons encore vérifier si quelque chose est hors en appelant les .log_prob_parts , ce qui donne l' log_prob de chaque nœud dans le modèle graphique:
mdl_ols.log_prob_parts(prior_predictive_samples)
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.9699239562734849>,
<tf.Tensor: shape=(), dtype=float64, numpy=-3.459364167569284>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.54574034, 0.4438451 , 0.05414307, 0.95995326, 0.62240687,
1.00021288, 0.39665739, 1.06465152, -0.27442125, 0.06750311,
0.95105078, 0.4828715 , -1.33977506, 0.33487533, 0.03618104,
-0.04785082, -0.03379069, 0.4412644 , 0.59901066, -0.2184827 ])>]
... il s'avère que le dernier nœud n'est pas en cours de réduction_somme le long de la dimension/axe iid ! Quand on fait la somme les deux premières variables sont donc mal diffusées.
L'astuce consiste à utiliser ici tfd.Independent pour réinterprété la forme de traitement par lots ( de sorte que le reste de l'axe sera réduite à juste titre ):
mdl_ols_ = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
# b1 shape: (batch_shape), X shape (num_obs): we want result to have
# shape (batch_shape, num_obs)
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
])
Maintenant, vérifions le dernier nœud/distribution du modèle, vous pouvez voir que la forme de l'événement est maintenant correctement interprétée. Notez que cela peut prendre un peu d'essais et d' erreurs pour obtenir le reinterpreted_batch_ndims droit, mais vous pouvez toujours imprimer facilement la distribution ou tenseur échantillonné vérifier la forme!
print(mdl_ols_.sample_distributions()[0][-1])
print(mdl_ols.sample_distributions()[0][-1])
tfp.distributions.Independent("JointDistributionSequential_sample_distributions_IndependentJointDistributionSequential_sample_distributions_Normal", batch_shape=[], event_shape=[20], dtype=float64)
tfp.distributions.Normal("JointDistributionSequential_sample_distributions_Normal", batch_shape=[20], event_shape=[], dtype=float64)
prior_predictive_samples = mdl_ols_.sample()
mdl_ols_.log_prob(prior_predictive_samples) # <== Getting a scalar correctly
<tf.Tensor: shape=(), dtype=float64, numpy=-2.543425661013286>
Autres JointDistribution* API
mdl_ols_named = tfd.JointDistributionNamed(dict(
likelihood = lambda b0, b1: tfd.Independent(
tfd.Normal(
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
b0 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
b1 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
))
mdl_ols_named.log_prob(mdl_ols_named.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-5.99620966071338>
mdl_ols_named.sample() # output is a dictionary
{'b0': <tf.Tensor: shape=(), dtype=float64, numpy=0.26364058399428225>,
'b1': <tf.Tensor: shape=(), dtype=float64, numpy=-0.27209402374432207>,
'likelihood': <tf.Tensor: shape=(20,), dtype=float64, numpy=
array([ 0.6482155 , -0.39314108, 0.62744764, -0.24587987, -0.20544617,
1.01465392, -0.04705611, -0.16618702, 0.36410134, 0.3943299 ,
0.36455291, -0.27822219, -0.24423928, 0.24599518, 0.82731092,
-0.21983033, 0.56753169, 0.32830481, -0.15713064, 0.23336351])>}
Root = tfd.JointDistributionCoroutine.Root # Convenient alias.
def model():
b1 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
b0 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
yhat = b0 + b1*X_np
likelihood = yield tfd.Independent(
tfd.Normal(loc=yhat, scale=sigma_y_np),
reinterpreted_batch_ndims=1
)
mdl_ols_coroutine = tfd.JointDistributionCoroutine(model)
mdl_ols_coroutine.log_prob(mdl_ols_coroutine.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-4.566678123520463>
mdl_ols_coroutine.sample() # output is a tuple
(<tf.Tensor: shape=(), dtype=float64, numpy=0.06811002171170354>,
<tf.Tensor: shape=(), dtype=float64, numpy=-0.37477064754116807>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.91615096, -0.20244718, -0.47840159, -0.26632479, -0.60441105,
-0.48977789, -0.32422329, -0.44019322, -0.17072643, -0.20666025,
-0.55932191, -0.40801868, -0.66893181, -0.24134135, -0.50403536,
-0.51788596, -0.90071876, -0.47382338, -0.34821655, -0.38559724])>)
MLE
Et nous pouvons maintenant faire de l'inférence ! Vous pouvez utiliser l'optimiseur pour trouver l'estimation de vraisemblance maximale.
Définir des fonctions d'assistance
# bfgs and lbfgs currently requries a function that returns both the value and
# gradient re the input.
import functools
def _make_val_and_grad_fn(value_fn):
@functools.wraps(value_fn)
def val_and_grad(x):
return tfp.math.value_and_gradient(value_fn, x)
return val_and_grad
# Map a list of tensors (e.g., output from JDSeq.sample([...])) to a single tensor
# modify from tfd.Blockwise
from tensorflow_probability.python.internal import dtype_util
from tensorflow_probability.python.internal import prefer_static as ps
from tensorflow_probability.python.internal import tensorshape_util
class Mapper:
"""Basically, this is a bijector without log-jacobian correction."""
def __init__(self, list_of_tensors, list_of_bijectors, event_shape):
self.dtype = dtype_util.common_dtype(
list_of_tensors, dtype_hint=tf.float32)
self.list_of_tensors = list_of_tensors
self.bijectors = list_of_bijectors
self.event_shape = event_shape
def flatten_and_concat(self, list_of_tensors):
def _reshape_map_part(part, event_shape, bijector):
part = tf.cast(bijector.inverse(part), self.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([
ps.shape(part)[:ps.size(ps.shape(part)) - ps.size(event_shape)],
[-1]
], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
list_of_tensors,
self.event_shape,
self.bijectors)
return tf.concat(tf.nest.flatten(x), axis=-1)
def split_and_reshape(self, x):
assertions = []
message = 'Input must have at least one dimension.'
if tensorshape_util.rank(x.shape) is not None:
if tensorshape_util.rank(x.shape) == 0:
raise ValueError(message)
else:
assertions.append(assert_util.assert_rank_at_least(x, 1, message=message))
with tf.control_dependencies(assertions):
splits = [
tf.cast(ps.maximum(1, ps.reduce_prod(s)), tf.int32)
for s in tf.nest.flatten(self.event_shape)
]
x = tf.nest.pack_sequence_as(
self.event_shape, tf.split(x, splits, axis=-1))
def _reshape_map_part(part, part_org, event_shape, bijector):
part = tf.cast(bijector.forward(part), part_org.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([ps.shape(part)[:-1], event_shape], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
x,
self.list_of_tensors,
self.event_shape,
self.bijectors)
return x
mapper = Mapper(mdl_ols_.sample()[:-1],
[tfb.Identity(), tfb.Identity()],
mdl_ols_.event_shape[:-1])
# mapper.split_and_reshape(mapper.flatten_and_concat(mdl_ols_.sample()[:-1]))
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input.
return -mdl_ols_.log_prob(mapper.split_and_reshape(x) + [Y_np])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=tf.zeros(2, dtype=dtype),
tolerance=1e-20,
x_tolerance=1e-8
)
b0est, b1est = lbfgs_results.position.numpy()
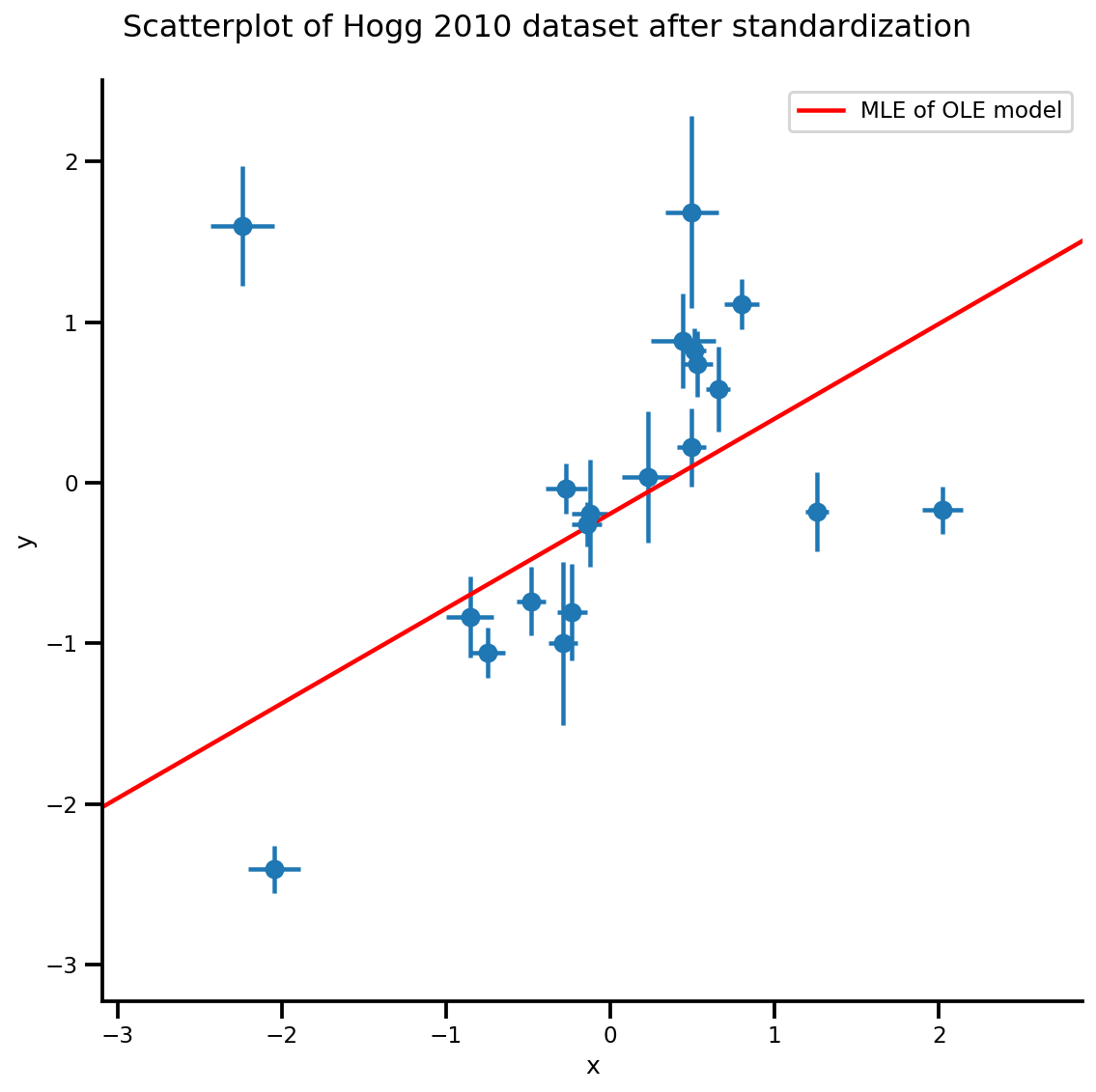
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of OLE model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
Modèle version batch et MCMC
Dans Inférence bayésienne, nous voulons habituellement travailler avec des échantillons MCMC, comme lorsque les échantillons sont de la partie postérieure, on peut les brancher dans une fonction aux attentes de calcul. Cependant, l'API MCMC nous obligent à écrire des modèles qui sont lot amical, et nous pouvons vérifier que notre modèle est en fait pas « batchable » en appelant l' sample([...])
mdl_ols_.sample(5) # <== error as some computation could not be broadcasted.
Dans ce cas, c'est relativement simple car nous n'avons qu'une fonction linéaire à l'intérieur de notre modèle, l'expansion de la forme devrait faire l'affaire :
mdl_ols_batch = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0[..., tf.newaxis] + b1[..., tf.newaxis]*X_np[tf.newaxis, ...],
scale=sigma_y_np[tf.newaxis, ...]),
reinterpreted_batch_ndims=1
),
])
mdl_ols_batch.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Nous pouvons à nouveau échantillonner et évaluer les log_prob_parts pour effectuer quelques vérifications :
b0, b1, y = mdl_ols_batch.sample(4)
mdl_ols_batch.log_prob_parts([b0, b1, y])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.25230168, -1.45281432, -1.87110061, -1.07665206])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.07019936, -1.59562117, -2.53387765, -1.01557632])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.45841406, 2.56829635, -4.84973951, -5.59423992])>]
Quelques notes latérales :
- Nous souhaitons travailler avec la version batch du modèle car c'est la plus rapide pour les MCMC multi-chaînes. Dans les cas que vous ne pouvez pas réécrire le modèle en version batched (par exemple, les modèles ODE), vous pouvez mapper la fonction log_prob en utilisant
tf.map_fnpour obtenir le même effet. - Maintenant
mdl_ols_batch.sample()peut ne pas fonctionner comme nous avons scaler avant, que nous ne pouvons passcaler_tensor[:, None]. La solution est ici pour élargir tenseur scaler rang 1 par emballagetfd.Sample(..., sample_shape=1). - C'est une bonne pratique d'écrire le modèle en tant que fonction afin que vous puissiez modifier les configurations comme les hyperparamètres beaucoup plus facilement.
def gen_ols_batch_model(X, sigma, hyperprior_mean=0, hyperprior_scale=1):
hyper_mean = tf.cast(hyperprior_mean, dtype)
hyper_scale = tf.cast(hyperprior_scale, dtype)
return tfd.JointDistributionSequential([
# b0
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# b1
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# likelihood
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0 + b1*X,
scale=sigma),
reinterpreted_batch_ndims=1
),
], validate_args=True)
mdl_ols_batch = gen_ols_batch_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
_ = mdl_ols_batch.sample()
_ = mdl_ols_batch.sample(4)
_ = mdl_ols_batch.sample([3, 4])
# Small helper function to validate log_prob shape (avoid wrong broadcasting)
def validate_log_prob_part(model, batch_shape=1, observed=-1):
samples = model.sample(batch_shape)
logp_part = list(model.log_prob_parts(samples))
# exclude observed node
logp_part.pop(observed)
for part in logp_part:
tf.assert_equal(part.shape, logp_part[-1].shape)
validate_log_prob_part(mdl_ols_batch, 4)
Plus de vérifications : comparaison de la fonction log_prob générée avec la fonction log_prob TFP écrite à la main.
def ols_logp_batch(b0, b1, Y):
b0_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b0
b1_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b1
likelihood = tfd.Normal(loc=b0 + b1*X_np[None, :],
scale=sigma_y_np) # likelihood
return tf.reduce_sum(b0_prior.log_prob(b0), axis=-1) +\
tf.reduce_sum(b1_prior.log_prob(b1), axis=-1) +\
tf.reduce_sum(likelihood.log_prob(Y), axis=-1)
b0, b1, x = mdl_ols_batch.sample(4)
print(mdl_ols_batch.log_prob([b0, b1, Y_np]).numpy())
print(ols_logp_batch(b0, b1, Y_np).numpy())
[-227.37899384 -327.10043743 -570.44162789 -702.79808683] [-227.37899384 -327.10043743 -570.44162789 -702.79808683]
MCMC utilisant l'échantillonneur No-U-Turn
A common run_chain fonction
@tf.function(autograph=False, experimental_compile=True)
def run_chain(init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
num_steps=500, burnin=50):
def trace_fn(_, pkr):
return (
pkr.inner_results.inner_results.target_log_prob,
pkr.inner_results.inner_results.leapfrogs_taken,
pkr.inner_results.inner_results.has_divergence,
pkr.inner_results.inner_results.energy,
pkr.inner_results.inner_results.log_accept_ratio
)
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.NoUTurnSampler(
target_log_prob_fn,
step_size=step_size),
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=burnin,
step_size_setter_fn=lambda pkr, new_step_size: pkr._replace(
inner_results=pkr.inner_results._replace(step_size=new_step_size)),
step_size_getter_fn=lambda pkr: pkr.inner_results.step_size,
log_accept_prob_getter_fn=lambda pkr: pkr.inner_results.log_accept_ratio
)
# Sampling from the chain.
chain_state, sampler_stat = tfp.mcmc.sample_chain(
num_results=num_steps,
num_burnin_steps=burnin,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
return chain_state, sampler_stat
nchain = 10
b0, b1, _ = mdl_ols_batch.sample(nchain)
init_state = [b0, b1]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1]]
target_log_prob_fn = lambda *x: mdl_ols_batch.log_prob(x + (Y_np, ))
# bijector to map contrained parameters to real
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
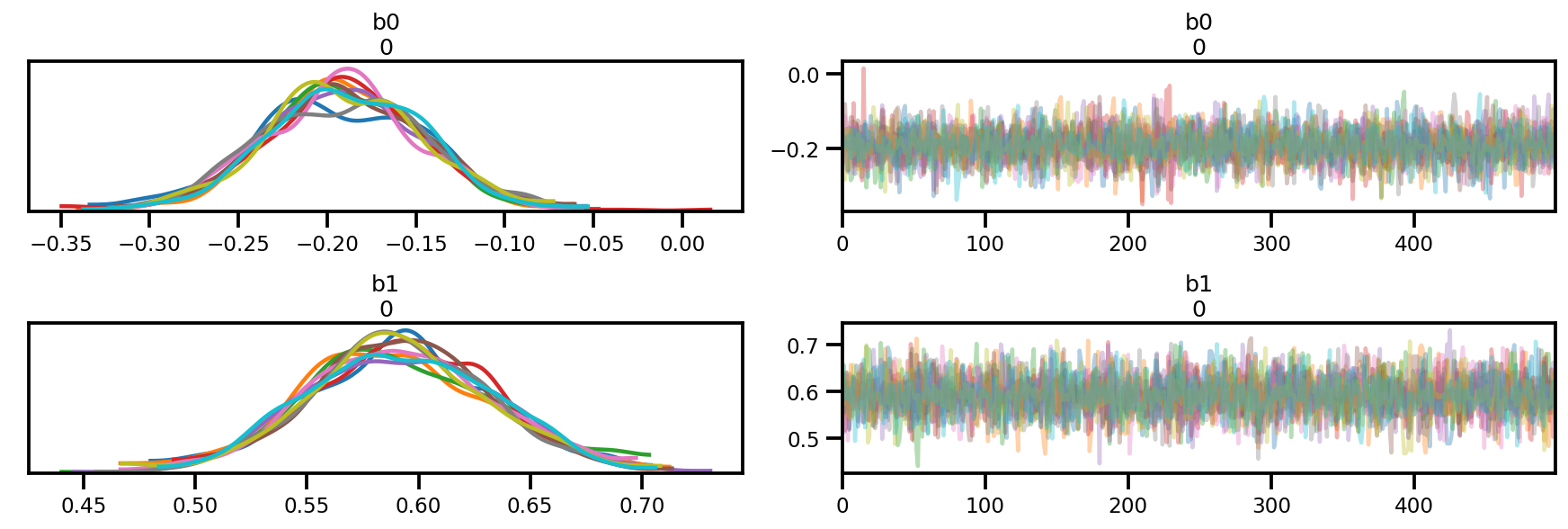
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace);
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
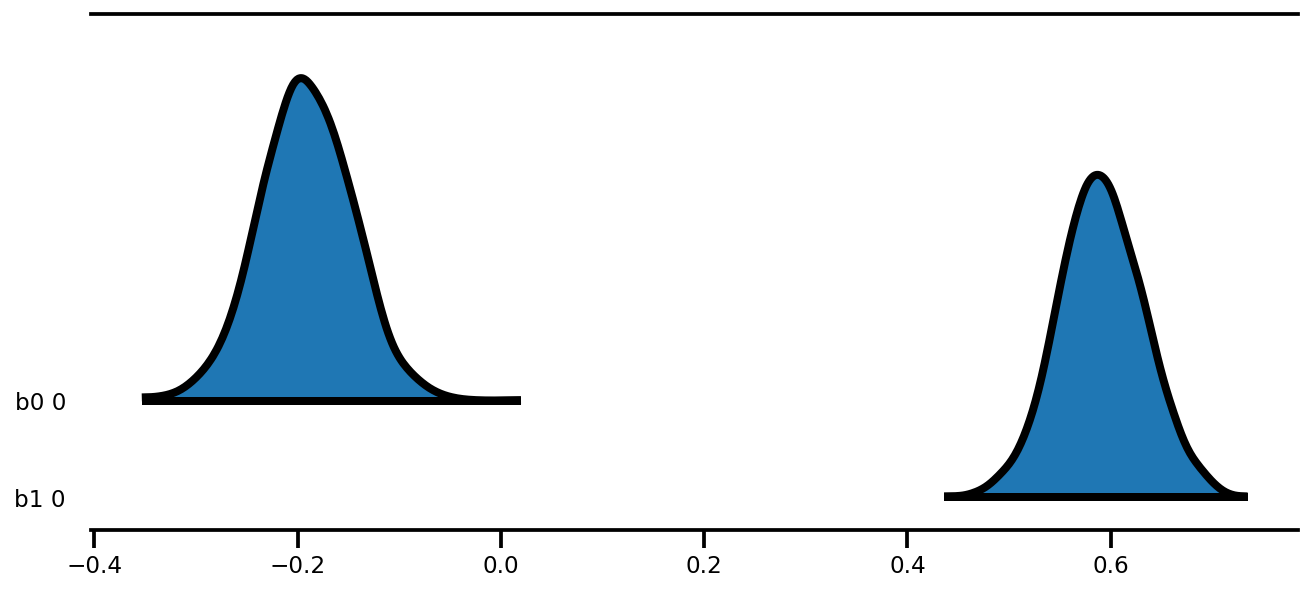
k = 5
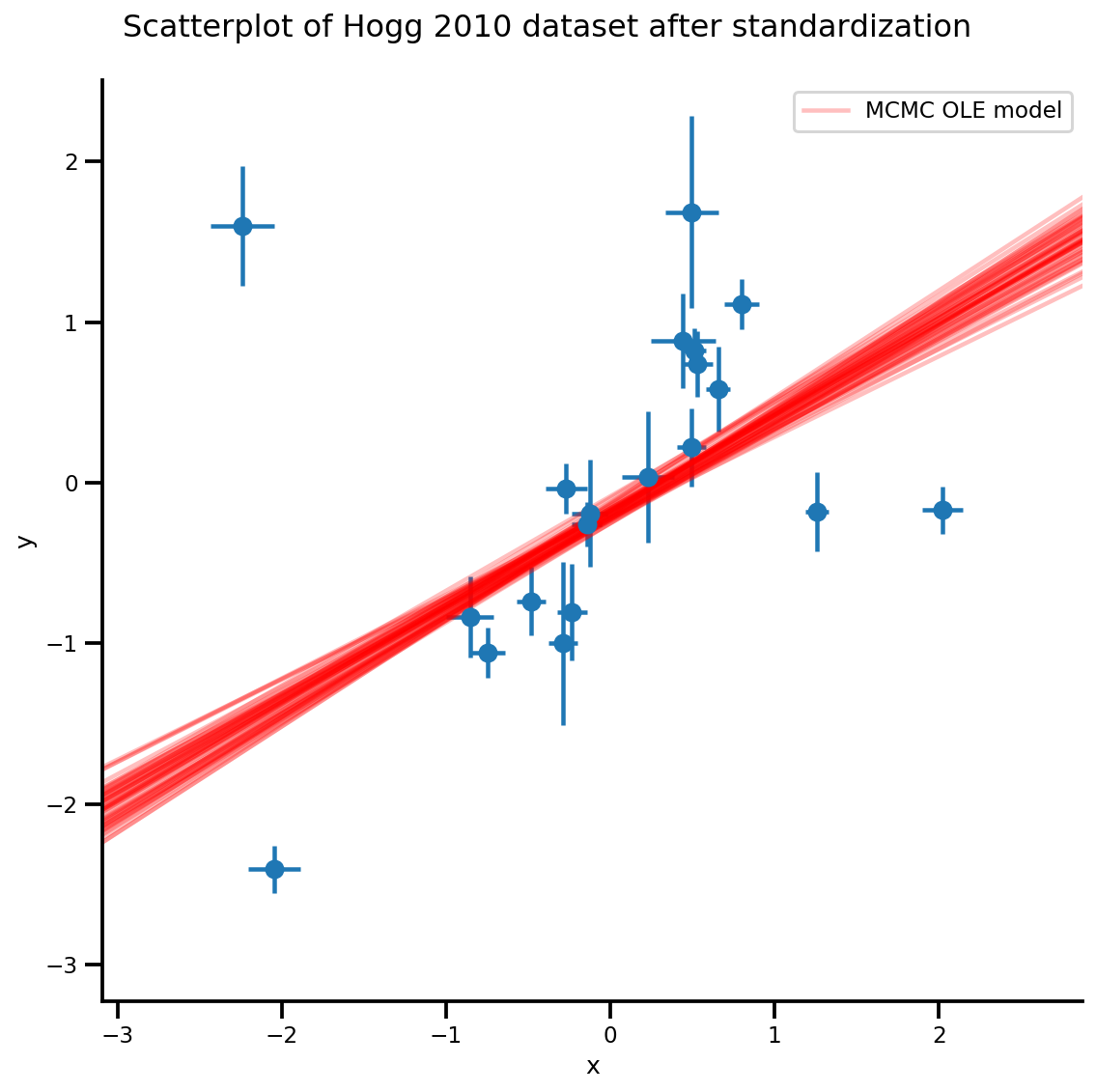
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC OLE model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Méthode Student-T
A noter qu'à partir de maintenant nous travaillons toujours avec la version batch d'un modèle
def gen_studentt_model(X, sigma,
hyper_mean=0, hyper_scale=1, lower=1, upper=100):
loc = tf.cast(hyper_mean, dtype)
scale = tf.cast(hyper_scale, dtype)
low = tf.cast(lower, dtype)
high = tf.cast(upper, dtype)
return tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# b1 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# df ~ Uniform(a, b)
tfd.Sample(tfd.Uniform(low, high), sample_shape=1),
# likelihood ~ StudentT(df, f(b0, b1), sigma_y)
# Using Independent to ensure the log_prob is not incorrectly broadcasted.
lambda df, b1, b0: tfd.Independent(
tfd.StudentT(df=df, loc=b0 + b1*X, scale=sigma)),
], validate_args=True)
mdl_studentt = gen_studentt_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
mdl_studentt.resolve_graph()
(('b0', ()), ('b1', ()), ('df', ()), ('x', ('df', 'b1', 'b0')))
validate_log_prob_part(mdl_studentt, 4)
Échantillon avant (échantillonnage prédictif préalable)
b0, b1, df, x = mdl_studentt.sample(1000)
x.shape
TensorShape([1000, 20])
MLE
# bijector to map contrained parameters to real
a, b = tf.constant(1., dtype), tf.constant(100., dtype),
# Interval transformation
tfp_interval = tfb.Inline(
inverse_fn=(
lambda x: tf.math.log(x - a) - tf.math.log(b - x)),
forward_fn=(
lambda y: (b - a) * tf.sigmoid(y) + a),
forward_log_det_jacobian_fn=(
lambda x: tf.math.log(b - a) - 2 * tf.nn.softplus(-x) - x),
forward_min_event_ndims=0,
name="interval")
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
tfp_interval,
]
mapper = Mapper(mdl_studentt.sample()[:-1],
unconstraining_bijectors,
mdl_studentt.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input, so we need to do some slicing here:
return -tf.squeeze(mdl_studentt.log_prob(
mapper.split_and_reshape(x) + [Y_np]))
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=mapper.flatten_and_concat(mdl_studentt.sample()[:-1]),
tolerance=1e-20,
x_tolerance=1e-20
)
b0est, b1est, dfest = lbfgs_results.position.numpy()
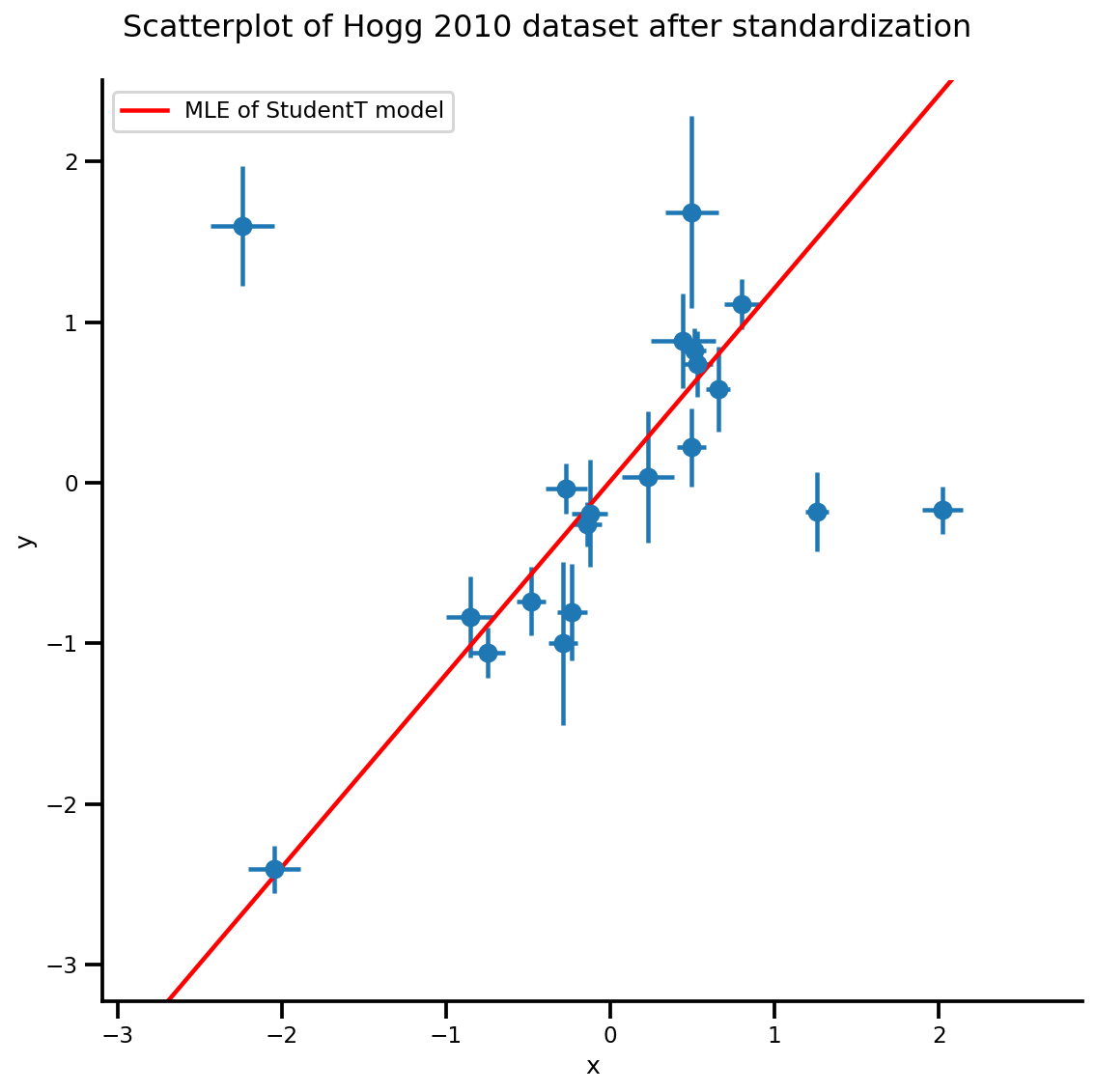
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of StudentT model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
MCMC
nchain = 10
b0, b1, df, _ = mdl_studentt.sample(nchain)
init_state = [b0, b1, df]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1, .05]]
target_log_prob_fn = lambda *x: mdl_studentt.log_prob(x + (Y_np, ))
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1', 'df']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.summary(az_trace)
az.plot_trace(az_trace);
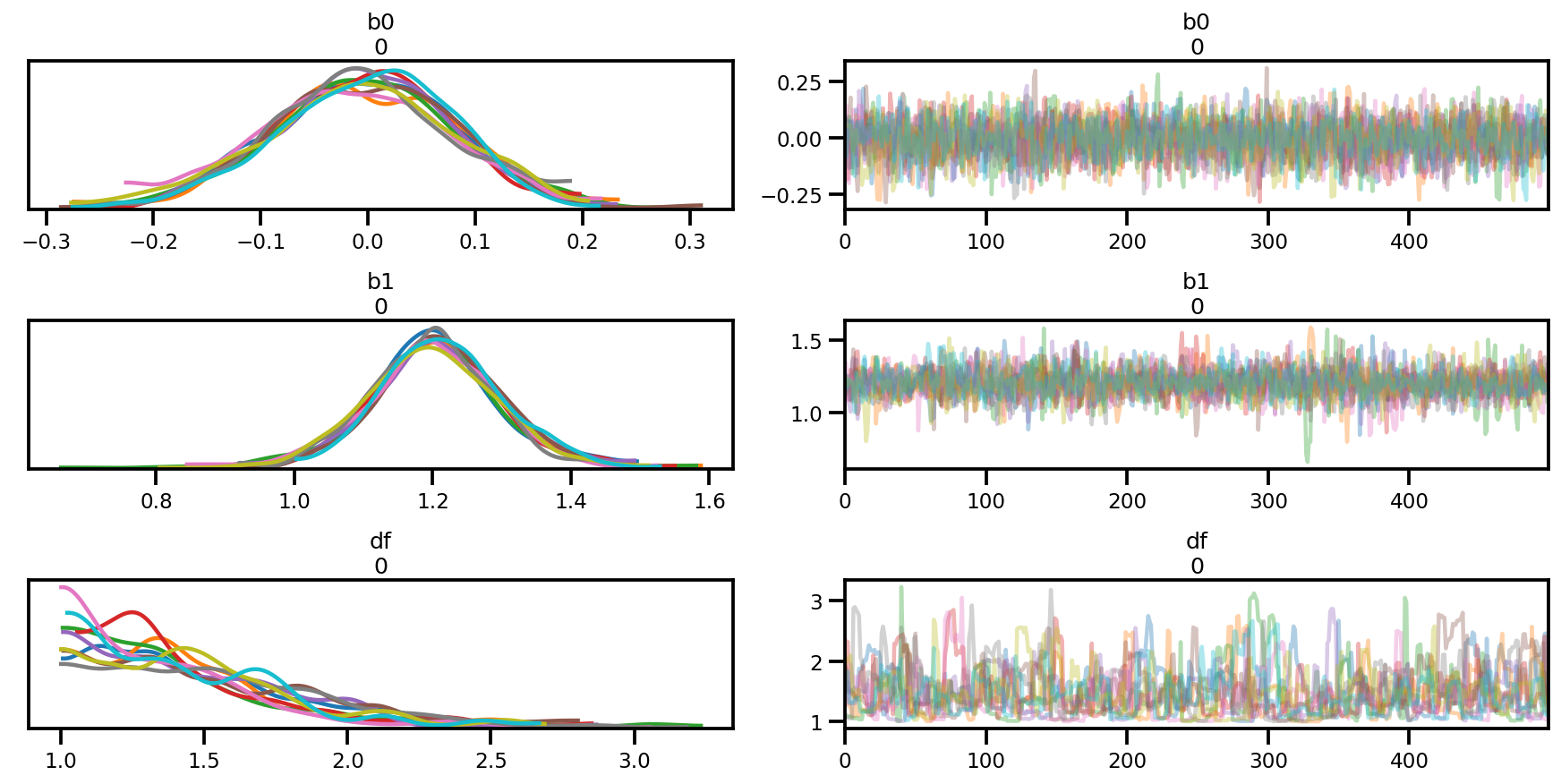
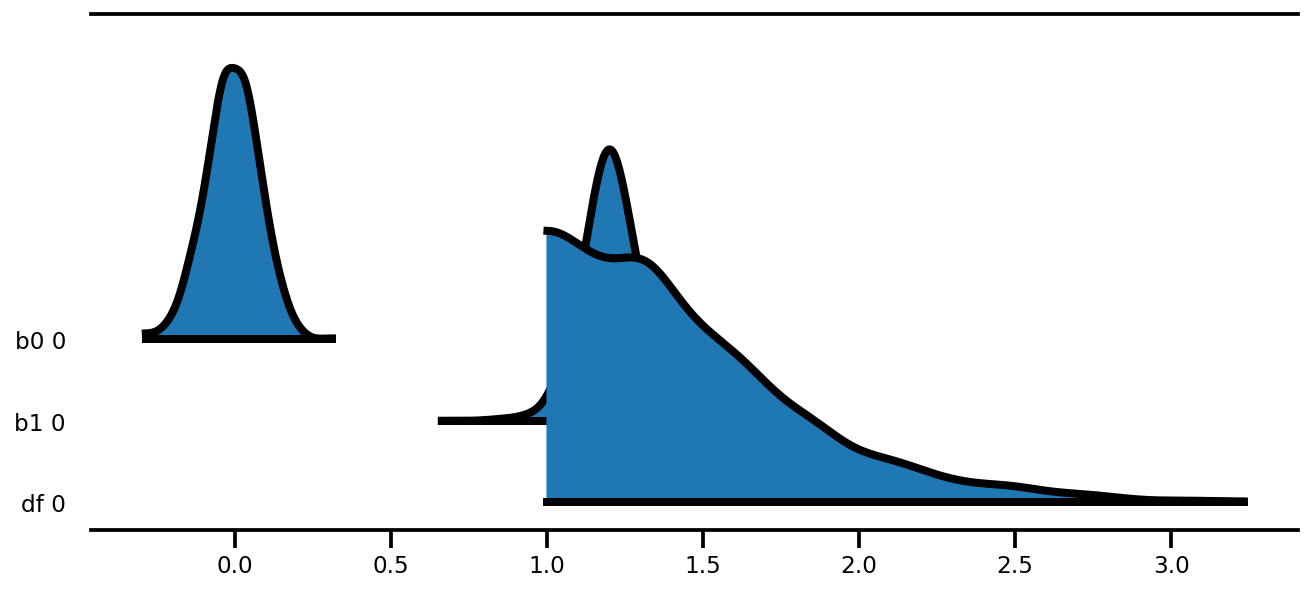
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
plt.hist(az_trace.sample_stats['tree_size'], np.linspace(.5, 25.5, 26), alpha=.5);
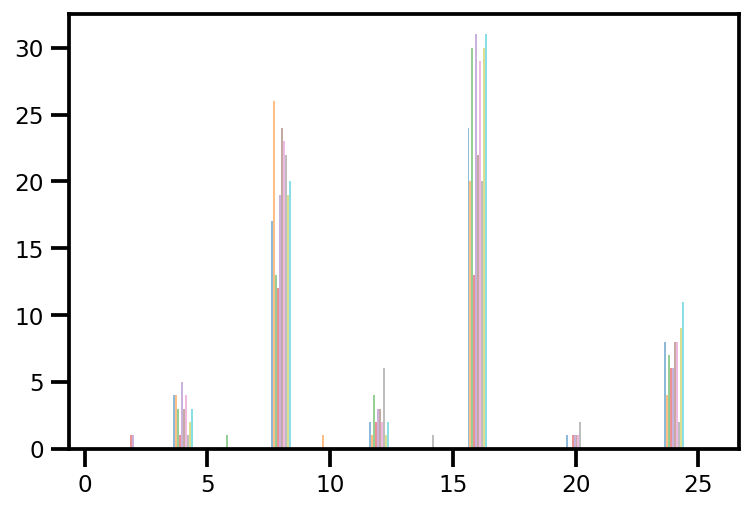
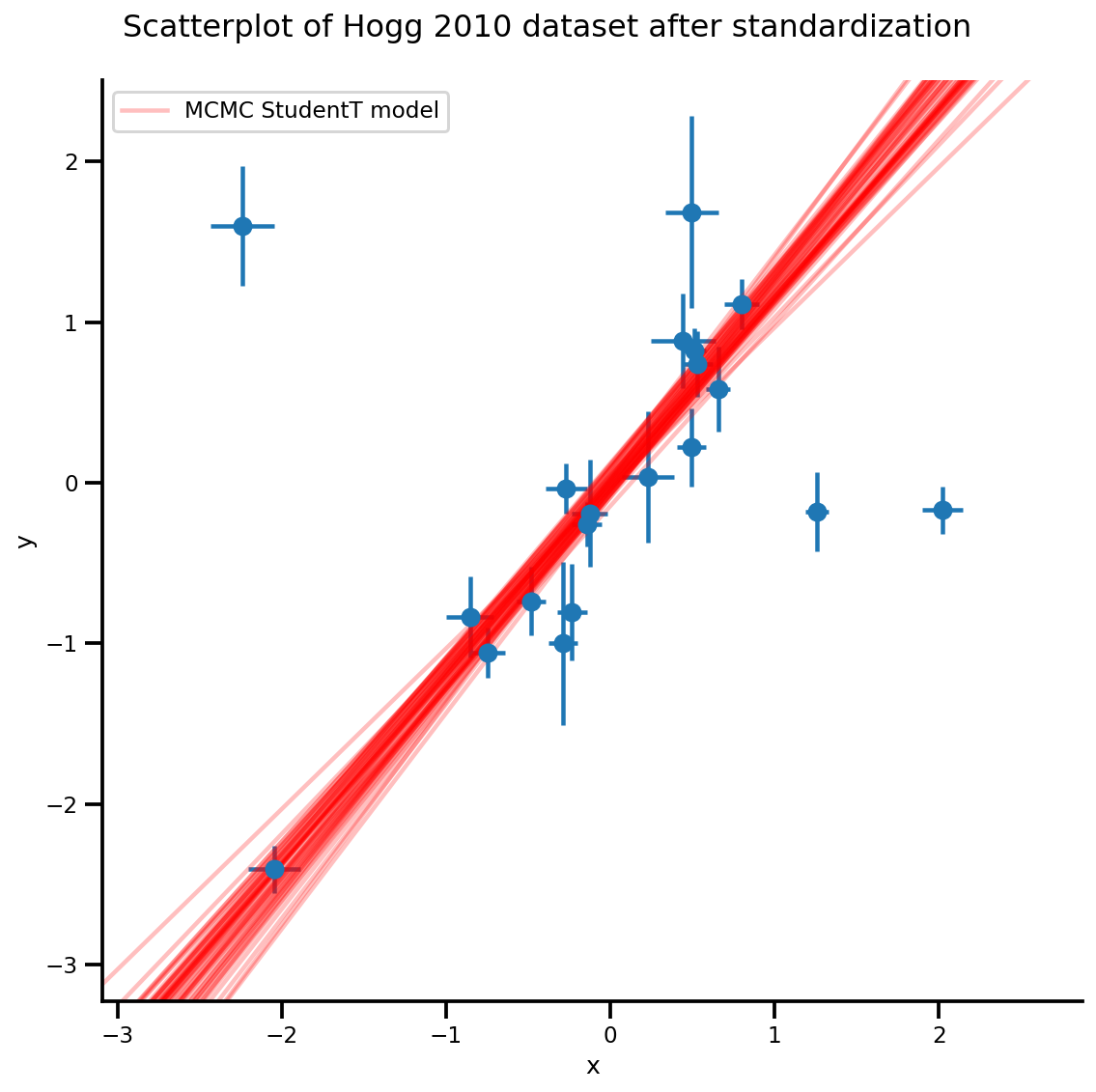
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC StudentT model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Mise en commun partielle hiérarchique
De PyMC3 données de base - ball pour 18 joueurs de Efron et Morris (1975)
data = pd.read_table('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/efron-morris-75-data.tsv',
sep="\t")
at_bats, hits = data[['At-Bats', 'Hits']].values.T
n = len(at_bats)
def gen_baseball_model(at_bats, rate=1.5, a=0, b=1):
return tfd.JointDistributionSequential([
# phi
tfd.Uniform(low=tf.cast(a, dtype), high=tf.cast(b, dtype)),
# kappa_log
tfd.Exponential(rate=tf.cast(rate, dtype)),
# thetas
lambda kappa_log, phi: tfd.Sample(
tfd.Beta(
concentration1=tf.exp(kappa_log)*phi,
concentration0=tf.exp(kappa_log)*(1.0-phi)),
sample_shape=n
),
# likelihood
lambda thetas: tfd.Independent(
tfd.Binomial(
total_count=tf.cast(at_bats, dtype),
probs=thetas
)),
])
mdl_baseball = gen_baseball_model(at_bats)
mdl_baseball.resolve_graph()
(('phi', ()),
('kappa_log', ()),
('thetas', ('kappa_log', 'phi')),
('x', ('thetas',)))
Échantillon avant (échantillonnage prédictif préalable)
phi, kappa_log, thetas, y = mdl_baseball.sample(4)
# phi, kappa_log, thetas, y
Encore une fois, remarquez que si vous n'utilisez pas Independent, vous vous retrouverez avec log_prob qui a une mauvaise batch_shape.
# check logp
pprint(mdl_baseball.log_prob_parts([phi, kappa_log, thetas, hits]))
print(mdl_baseball.log_prob([phi, kappa_log, thetas, hits]))
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([0., 0., 0., 0.])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.1721297 , -0.95946498, -0.72591188, 0.23993813])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([59.35192283, 7.0650634 , 0.83744911, 74.14370935])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3279.75191016, -931.10438484, -512.59197688, -1131.08043597])>] tf.Tensor([-3220.22785762 -924.99878641 -512.48043966 -1056.69678849], shape=(4,), dtype=float64)
MLE
Une jolie caractéristique étonnante de tfp.optimizer est que, vous pouvez optimiser en parallèle pour le lot k de point de départ et spécifiez le stopping_condition kwarg: vous pouvez le mettre à tfp.optimizer.converged_all pour voir s'ils trouvent tout de même minime, ou tfp.optimizer.converged_any pour trouver rapidement une solution locale.
unconstraining_bijectors = [
tfb.Sigmoid(),
tfb.Exp(),
tfb.Sigmoid(),
]
phi, kappa_log, thetas, y = mdl_baseball.sample(10)
mapper = Mapper([phi, kappa_log, thetas],
unconstraining_bijectors,
mdl_baseball.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
return -mdl_baseball.log_prob(mapper.split_and_reshape(x) + [hits])
start = mapper.flatten_and_concat([phi, kappa_log, thetas])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
num_correction_pairs=10,
initial_position=start,
# lbfgs actually can work in batch as well
stopping_condition=tfp.optimizer.converged_any,
tolerance=1e-50,
x_tolerance=1e-50,
parallel_iterations=10,
max_iterations=200
)
lbfgs_results.converged.numpy(), lbfgs_results.failed.numpy()
(array([False, False, False, False, False, False, False, False, False,
False]),
array([ True, True, True, True, True, True, True, True, True,
True]))
result = lbfgs_results.position[lbfgs_results.converged & ~lbfgs_results.failed]
result
<tf.Tensor: shape=(0, 20), dtype=float64, numpy=array([], shape=(0, 20), dtype=float64)>
LBFGS n'a pas convergé.
if result.shape[0] > 0:
phi_est, kappa_est, theta_est = mapper.split_and_reshape(result)
phi_est, kappa_est, theta_est
MCMC
target_log_prob_fn = lambda *x: mdl_baseball.log_prob(x + (hits, ))
nchain = 4
phi, kappa_log, thetas, _ = mdl_baseball.sample(nchain)
init_state = [phi, kappa_log, thetas]
step_size=[tf.cast(i, dtype=dtype) for i in [.1, .1, .1]]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
burnin=200)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['phi', 'kappa_log', 'thetas']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
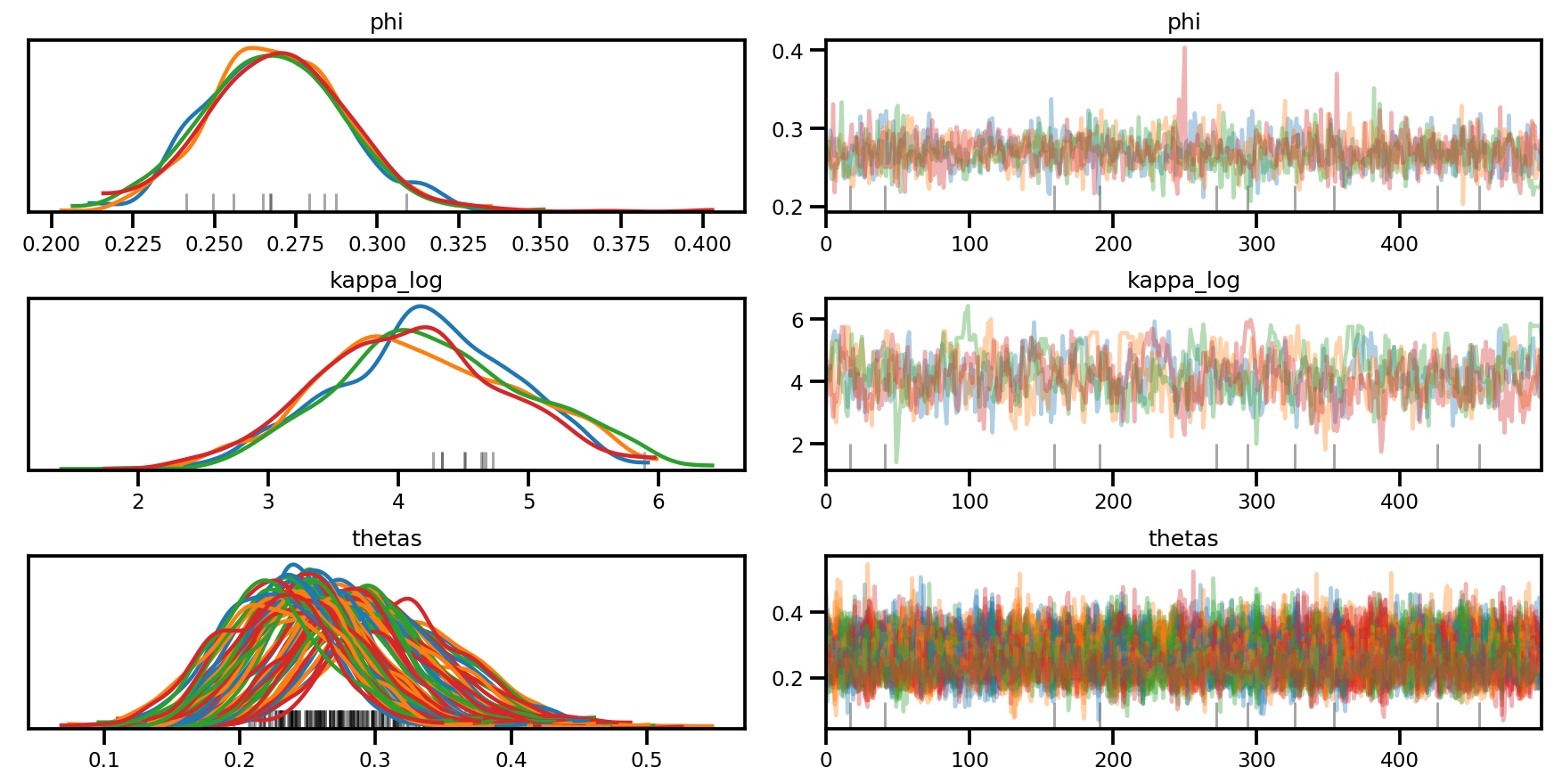
az.plot_trace(az_trace, compact=True);
az.plot_forest(az_trace,
var_names=['thetas'],
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 8));
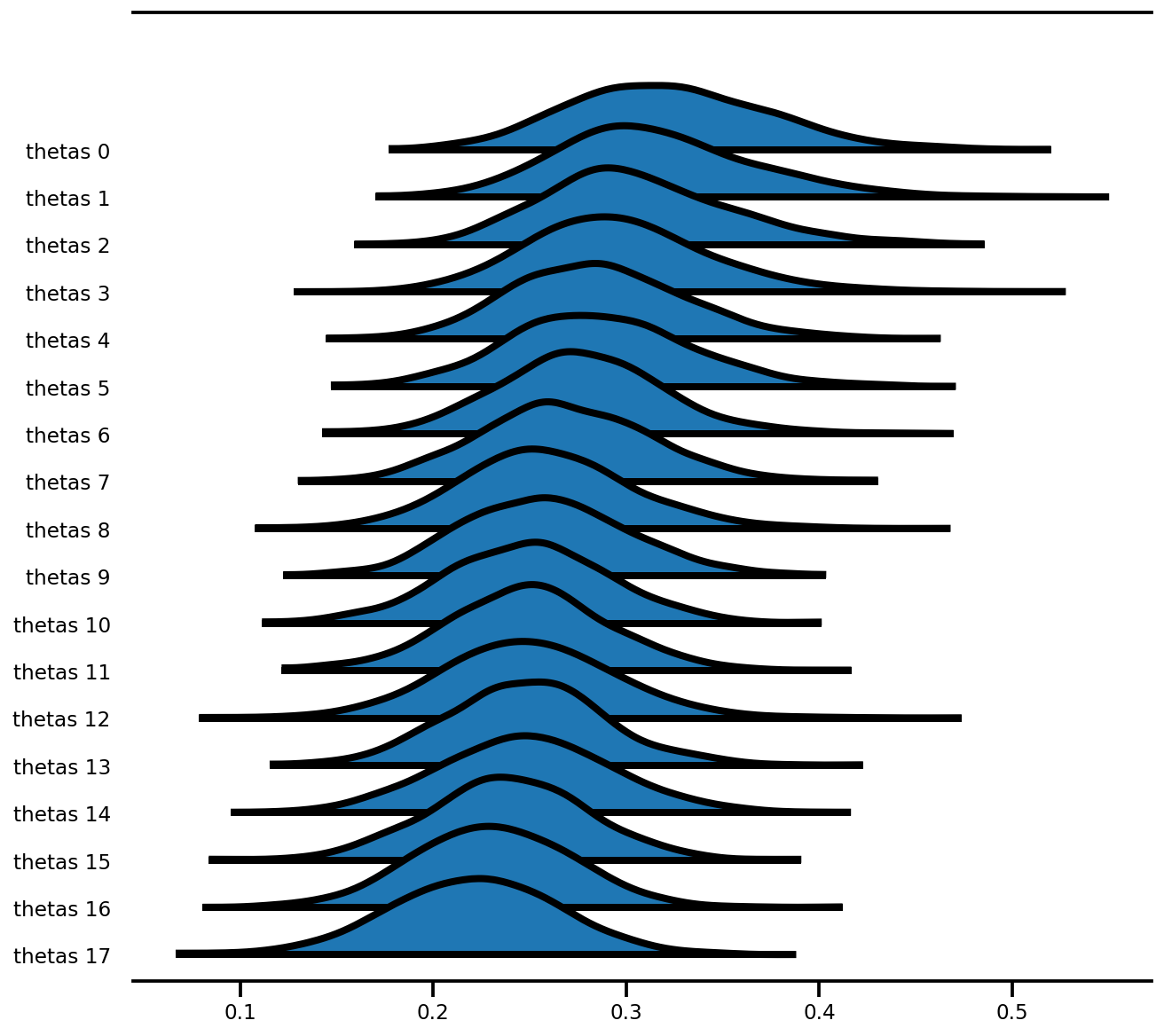
Modèle à effet mixte (Radon)
Le dernier modèle dans le PyMC3 doc: Notions élémentaires sur les méthodes bayésienne pour la modélisation multi - niveaux
Quelques changements dans l'antériorité (plus petite échelle, etc.)
Charger les données brutes et nettoyer
srrs2 = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/srrs2.dat')
srrs2.columns = srrs2.columns.map(str.strip)
srrs_mn = srrs2[srrs2.state=='MN'].copy()
srrs_mn['fips'] = srrs_mn.stfips*1000 + srrs_mn.cntyfips
cty = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/cty.dat')
cty_mn = cty[cty.st=='MN'].copy()
cty_mn[ 'fips'] = 1000*cty_mn.stfips + cty_mn.ctfips
srrs_mn = srrs_mn.merge(cty_mn[['fips', 'Uppm']], on='fips')
srrs_mn = srrs_mn.drop_duplicates(subset='idnum')
u = np.log(srrs_mn.Uppm)
n = len(srrs_mn)
srrs_mn.county = srrs_mn.county.map(str.strip)
mn_counties = srrs_mn.county.unique()
counties = len(mn_counties)
county_lookup = dict(zip(mn_counties, range(len(mn_counties))))
county = srrs_mn['county_code'] = srrs_mn.county.replace(county_lookup).values
radon = srrs_mn.activity
srrs_mn['log_radon'] = log_radon = np.log(radon + 0.1).values
floor_measure = srrs_mn.floor.values.astype('float')
# Create new variable for mean of floor across counties
xbar = srrs_mn.groupby('county')['floor'].mean().rename(county_lookup).values
Pour les modèles avec une transformation complexe, l'implémenter dans un style fonctionnel rendrait l'écriture et les tests beaucoup plus faciles. En outre, cela permet de générer par programme la fonction log_prob qui dépend (mini-lot) des données saisies beaucoup plus facilement :
def affine(u_val, x_county, county, floor, gamma, eps, b):
"""Linear equation of the coefficients and the covariates, with broadcasting."""
return (tf.transpose((gamma[..., 0]
+ gamma[..., 1]*u_val[:, None]
+ gamma[..., 2]*x_county[:, None]))
+ tf.gather(eps, county, axis=-1)
+ b*floor)
def gen_radon_model(u_val, x_county, county, floor,
mu0=tf.zeros([], dtype, name='mu0')):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
# sigma_a
tfd.HalfCauchy(loc=mu0, scale=5.),
# eps
lambda sigma_a: tfd.Sample(
tfd.Normal(loc=mu0, scale=sigma_a), sample_shape=counties),
# gamma
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=3),
# b
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=1),
# sigma_y
tfd.Sample(tfd.HalfCauchy(loc=mu0, scale=5.), sample_shape=1),
# likelihood
lambda sigma_y, b, gamma, eps: tfd.Independent(
tfd.Normal(
loc=affine(u_val, x_county, county, floor, gamma, eps, b),
scale=sigma_y
),
reinterpreted_batch_ndims=1
),
])
contextual_effect2 = gen_radon_model(
u.values, xbar[county], county, floor_measure)
@tf.function(autograph=False)
def unnormalized_posterior_log_prob(sigma_a, gamma, eps, b, sigma_y):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return contextual_effect2.log_prob(
[sigma_a, gamma, eps, b, sigma_y, log_radon])
assert [4] == unnormalized_posterior_log_prob(
*contextual_effect2.sample(4)[:-1]).shape
samples = contextual_effect2.sample(4)
pprint([s.shape for s in samples])
[TensorShape([4]), TensorShape([4, 85]), TensorShape([4, 3]), TensorShape([4, 1]), TensorShape([4, 1]), TensorShape([4, 919])]
contextual_effect2.log_prob_parts(list(samples)[:-1] + [log_radon])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3.95681828, -2.45693443, -2.53310078, -4.7717536 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-340.65975204, -217.11139018, -246.50498667, -369.79687704])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-20.49822449, -20.38052557, -18.63843525, -17.83096972])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-5.94765605, -5.91460848, -6.66169402, -5.53894593])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-2.10293999, -4.34186631, -2.10744955, -3.016717 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=
array([-29022322.1413861 , -114422.36893361, -8708500.81752865,
-35061.92497235])>]
Inférence variationnelle
Une caractéristique très puissante de JointDistribution* est que vous pouvez générer une approximation facilement VI. Par exemple, pour effectuer un ADVI à champ moyen, vous inspectez simplement le graphique et remplacez toute la distribution non observée par une distribution normale.
Champ moyen ADVI
Vous pouvez également utiliser la fonction experimential dans tensorflow_probability / python / expérimental / vi pour construire variationnelle, qui sont essentiellement la même logique utilisée ci - dessous (à l'aide JointDistribution pour construire approximation), mais avec la sortie d'approximation dans l'espace d' origine au lieu du espace illimité.
from tensorflow_probability.python.mcmc.transformed_kernel import (
make_transform_fn, make_transformed_log_prob)
# Wrap logp so that all parameters are in the Real domain
# copied and edited from tensorflow_probability/python/mcmc/transformed_kernel.py
unconstraining_bijectors = [
tfb.Exp(),
tfb.Identity(),
tfb.Identity(),
tfb.Identity(),
tfb.Exp()
]
unnormalized_log_prob = lambda *x: contextual_effect2.log_prob(x + (log_radon,))
contextual_effect_posterior = make_transformed_log_prob(
unnormalized_log_prob,
unconstraining_bijectors,
direction='forward',
# TODO(b/72831017): Disable caching until gradient linkage
# generally works.
enable_bijector_caching=False)
# debug
if True:
# Check the two versions of log_prob - they should be different given the Jacobian
rv_samples = contextual_effect2.sample(4)
_inverse_transform = make_transform_fn(unconstraining_bijectors, 'inverse')
_forward_transform = make_transform_fn(unconstraining_bijectors, 'forward')
pprint([
unnormalized_log_prob(*rv_samples[:-1]),
contextual_effect_posterior(*_inverse_transform(rv_samples[:-1])),
unnormalized_log_prob(
*_forward_transform(
tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1])
),
contextual_effect_posterior(
*[tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1]]
),
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73354969e+04, -5.51622488e+04, -2.77754609e+08, -1.09065161e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73331358e+04, -5.51582029e+04, -2.77754602e+08, -1.09065134e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>]
# Build meanfield ADVI for a jointdistribution
# Inspect the input jointdistribution and replace the list of distribution with
# a list of Normal distribution, each with the same shape.
def build_meanfield_advi(jd_list, observed_node=-1):
"""
The inputted jointdistribution needs to be a batch version
"""
# Sample to get a list of Tensors
list_of_values = jd_list.sample(1) # <== sample([]) might not work
# Remove the observed node
list_of_values.pop(observed_node)
# Iterate the list of Tensor to a build a list of Normal distribution (i.e.,
# the Variational posterior)
distlist = []
for i, value in enumerate(list_of_values):
dtype = value.dtype
rv_shape = value[0].shape
loc = tf.Variable(
tf.random.normal(rv_shape, dtype=dtype),
name='meanfield_%s_mu' % i,
dtype=dtype)
scale = tfp.util.TransformedVariable(
tf.fill(rv_shape, value=tf.constant(0.02, dtype)),
tfb.Softplus(),
name='meanfield_%s_scale' % i,
)
approx_node = tfd.Normal(loc=loc, scale=scale)
if loc.shape == ():
distlist.append(approx_node)
else:
distlist.append(
# TODO: make the reinterpreted_batch_ndims more flexible (for
# minibatch etc)
tfd.Independent(approx_node, reinterpreted_batch_ndims=1)
)
# pass list to JointDistribution to initiate the meanfield advi
meanfield_advi = tfd.JointDistributionSequential(distlist)
return meanfield_advi
advi = build_meanfield_advi(contextual_effect2, observed_node=-1)
# Check the logp and logq
advi_samples = advi.sample(4)
pprint([
advi.log_prob(advi_samples),
contextual_effect_posterior(*advi_samples)
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([231.26836839, 229.40755095, 227.10287879, 224.05914594])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-10615.93542431, -11743.21420129, -10376.26732337, -11338.00600103])>]
opt = tf.optimizers.Adam(learning_rate=.1)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior,
surrogate_posterior=advi,
optimizer=opt,
sample_size=10,
num_steps=300)
return loss_
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
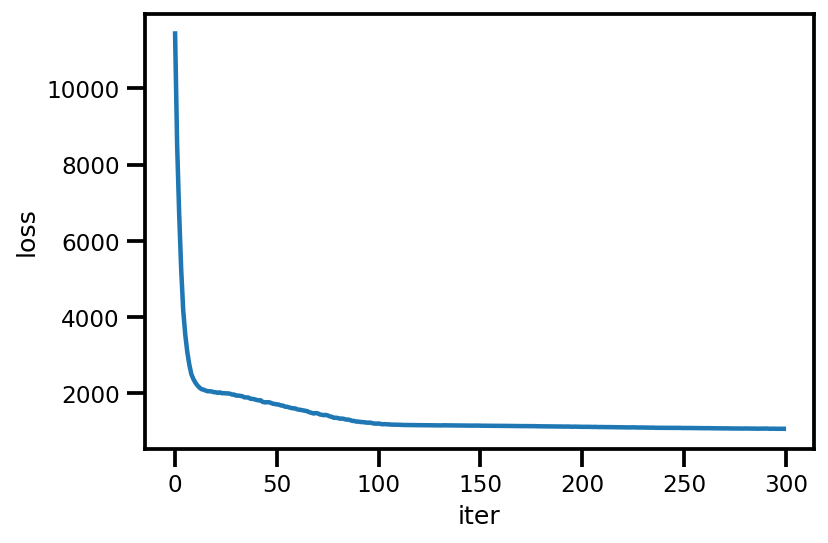
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param = advi.trainable_variables
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param[i*2].numpy(),
"sd": free_param[i*2+1].numpy()}
approx_param.keys()
dict_keys(['sigma_a', 'eps', 'gamma', 'b', 'sigma_y'])
approx_param['gamma']
{'mu': array([1.28145814, 0.70365287, 1.02689857]),
'sd': array([-3.6604972 , -2.68153218, -2.04176524])}
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
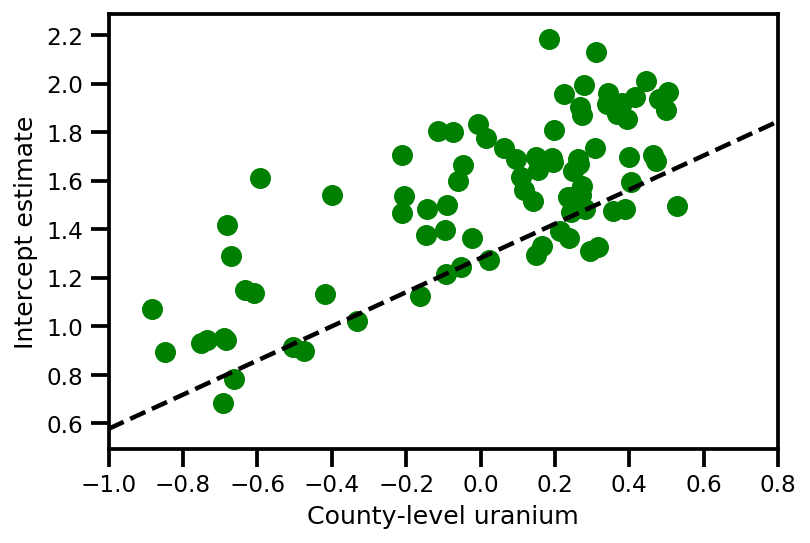
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
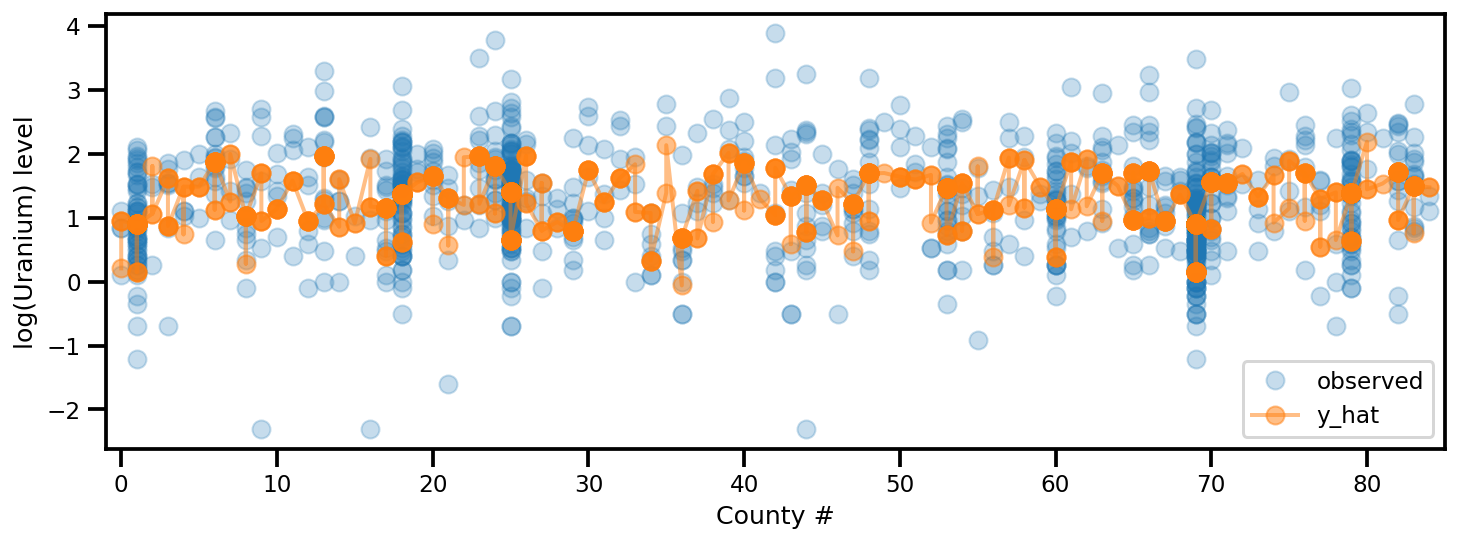
Rang complet ADVI
Pour un ADVI de rang complet, nous voulons approximer le postérieur avec une gaussienne multivariée.
USE_FULLRANK = True
*prior_tensors, _ = contextual_effect2.sample()
mapper = Mapper(prior_tensors,
[tfb.Identity() for _ in prior_tensors],
contextual_effect2.event_shape[:-1])
rv_shape = ps.shape(mapper.flatten_and_concat(mapper.list_of_tensors))
init_val = tf.random.normal(rv_shape, dtype=dtype)
loc = tf.Variable(init_val, name='loc', dtype=dtype)
if USE_FULLRANK:
# cov_param = tfp.util.TransformedVariable(
# 10. * tf.eye(rv_shape[0], dtype=dtype),
# tfb.FillScaleTriL(),
# name='cov_param'
# )
FillScaleTriL = tfb.FillScaleTriL(
diag_bijector=tfb.Chain([
tfb.Shift(tf.cast(.01, dtype)),
tfb.Softplus(),
tfb.Shift(tf.cast(np.log(np.expm1(1.)), dtype))]),
diag_shift=None)
cov_param = tfp.util.TransformedVariable(
.02 * tf.eye(rv_shape[0], dtype=dtype),
FillScaleTriL,
name='cov_param')
advi_approx = tfd.MultivariateNormalTriL(
loc=loc, scale_tril=cov_param)
else:
# An alternative way to build meanfield ADVI.
cov_param = tfp.util.TransformedVariable(
.02 * tf.ones(rv_shape, dtype=dtype),
tfb.Softplus(),
name='cov_param'
)
advi_approx = tfd.MultivariateNormalDiag(
loc=loc, scale_diag=cov_param)
contextual_effect_posterior2 = lambda x: contextual_effect_posterior(
*mapper.split_and_reshape(x)
)
# Check the logp and logq
advi_samples = advi_approx.sample(7)
pprint([
advi_approx.log_prob(advi_samples),
contextual_effect_posterior2(advi_samples)
])
[<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([238.81841799, 217.71022639, 234.57207103, 230.0643819 ,
243.73140943, 226.80149702, 232.85184209])>,
<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([-3638.93663169, -3664.25879314, -3577.69371677, -3696.25705312,
-3689.12130489, -3777.53698383, -3659.4982734 ])>]
learning_rate = tf.optimizers.schedules.ExponentialDecay(
initial_learning_rate=1e-2,
decay_steps=10,
decay_rate=0.99,
staircase=True)
opt = tf.optimizers.Adam(learning_rate=learning_rate)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior2,
surrogate_posterior=advi_approx,
optimizer=opt,
sample_size=10,
num_steps=1000)
return loss_
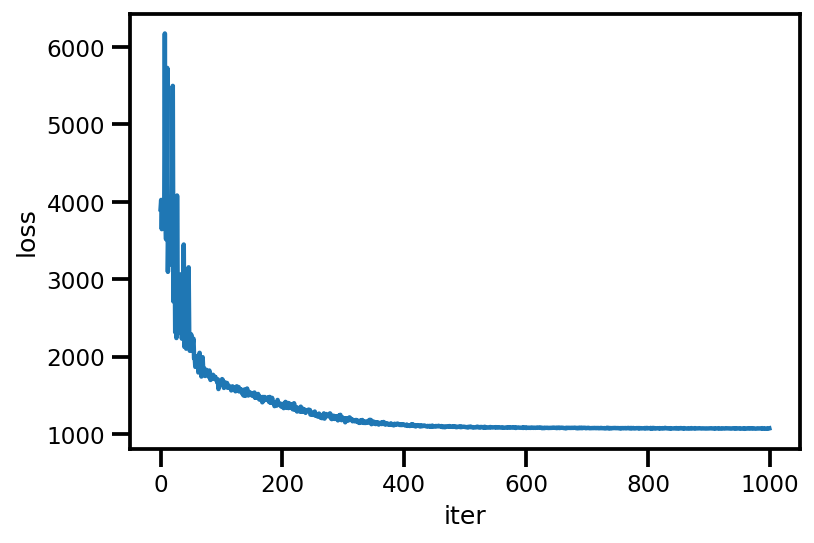
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
# debug
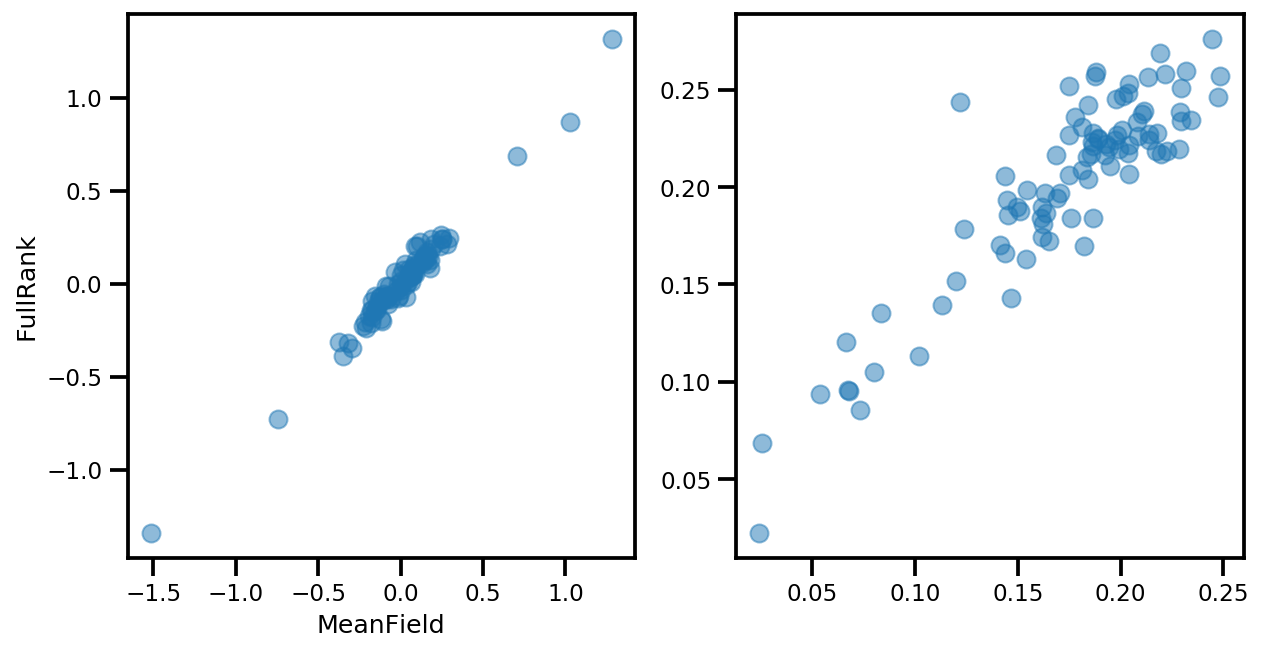
if True:
_, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(mapper.flatten_and_concat(advi.mean()), advi_approx.mean(), 'o', alpha=.5)
ax[1].plot(mapper.flatten_and_concat(advi.stddev()), advi_approx.stddev(), 'o', alpha=.5)
ax[0].set_xlabel('MeanField')
ax[0].set_ylabel('FullRank')
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param_mean = mapper.split_and_reshape(advi_approx.mean())
free_param_std = mapper.split_and_reshape(advi_approx.stddev())
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param_mean[i].numpy(),
"cov_info": free_param_std[i].numpy()}
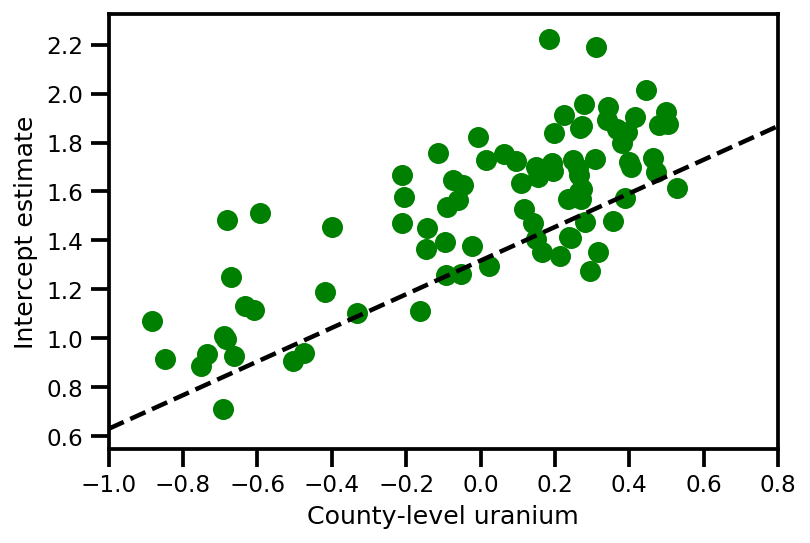
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
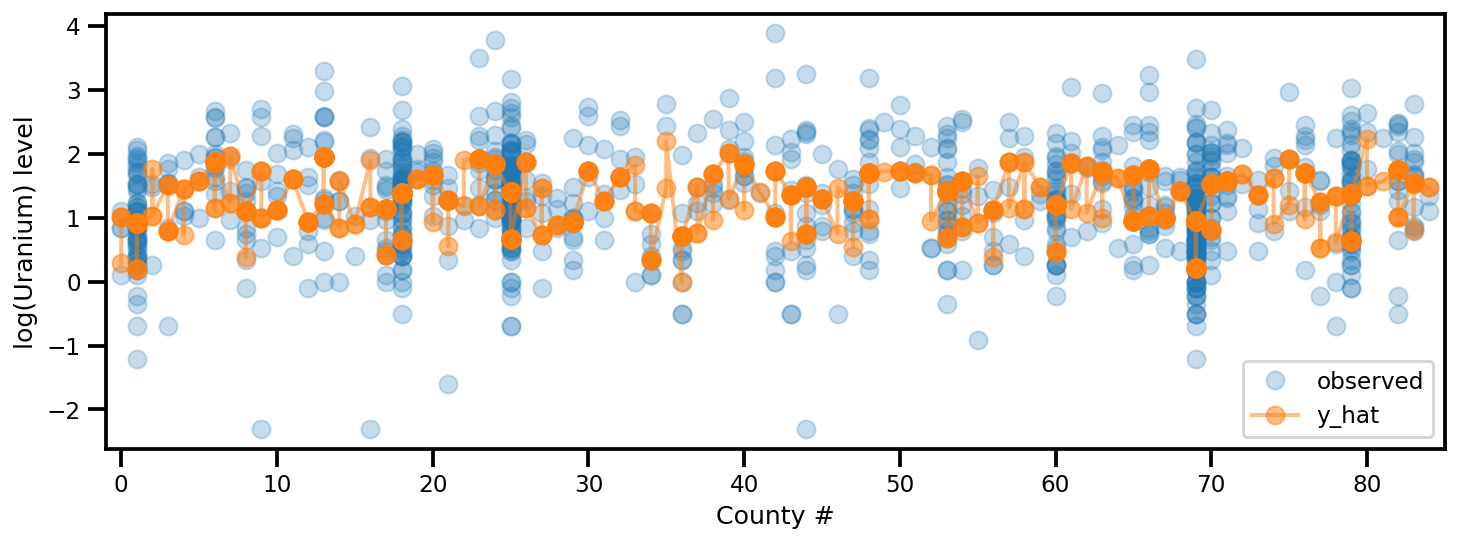
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
Modèle de mélange Beta-Bernoulli
Un modèle de mélange où plusieurs réviseurs étiquettent certains éléments, avec des étiquettes latentes inconnues (vraies).
dtype = tf.float32
n = 50000 # number of examples reviewed
p_bad_ = 0.1 # fraction of bad events
m = 5 # number of reviewers for each example
rcl_ = .35 + np.random.rand(m)/10
prc_ = .65 + np.random.rand(m)/10
# PARAMETER TRANSFORMATION
tpr = rcl_
fpr = p_bad_*tpr*(1./prc_-1.)/(1.-p_bad_)
tnr = 1 - fpr
# broadcast to m reviewer.
batch_prob = np.asarray([tpr, fpr]).T
mixture = tfd.Mixture(
tfd.Categorical(
probs=[p_bad_, 1-p_bad_]),
[
tfd.Independent(tfd.Bernoulli(probs=tpr), 1),
tfd.Independent(tfd.Bernoulli(probs=fpr), 1),
])
# Generate reviewer response
X_tf = mixture.sample([n])
# run once to always use the same array as input
# so we can compare the estimation from different
# inference method.
X_np = X_tf.numpy()
# batched Mixture model
mdl_mixture = tfd.JointDistributionSequential([
tfd.Sample(tfd.Beta(5., 2.), m),
tfd.Sample(tfd.Beta(2., 2.), m),
tfd.Sample(tfd.Beta(1., 10), 1),
lambda p_bad, rcl, prc: tfd.Sample(
tfd.Mixture(
tfd.Categorical(
probs=tf.concat([p_bad, 1.-p_bad], -1)),
[
tfd.Independent(tfd.Bernoulli(
probs=rcl), 1),
tfd.Independent(tfd.Bernoulli(
probs=p_bad*rcl*(1./prc-1.)/(1.-p_bad)), 1)
]
), (n, )),
])
mdl_mixture.resolve_graph()
(('prc', ()), ('rcl', ()), ('p_bad', ()), ('x', ('p_bad', 'rcl', 'prc')))
prc, rcl, p_bad, x = mdl_mixture.sample(4)
x.shape
TensorShape([4, 50000, 5])
mdl_mixture.log_prob_parts([prc, rcl, p_bad, X_np[np.newaxis, ...]])
[<tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.4828572, 2.957961 , 2.9355168, 2.6116824], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.14646745, 1.3308513 , 1.1205603 , 0.5441705 ], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.3733709, 1.8020535, 2.1865845, 1.5701319], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-54326.664, -52683.93 , -64407.67 , -55007.895], dtype=float32)>]
Inférence (NUTS)
nchain = 10
prc, rcl, p_bad, _ = mdl_mixture.sample(nchain)
initial_chain_state = [prc, rcl, p_bad]
# Since MCMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
unconstraining_bijectors = [
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
]
step_size = [tf.cast(i, dtype=dtype) for i in [1e-3, 1e-3, 1e-3]]
X_expanded = X_np[np.newaxis, ...]
target_log_prob_fn = lambda *x: mdl_mixture.log_prob(x + (X_expanded, ))
samples, sampler_stat = run_chain(
initial_chain_state, step_size, target_log_prob_fn,
unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
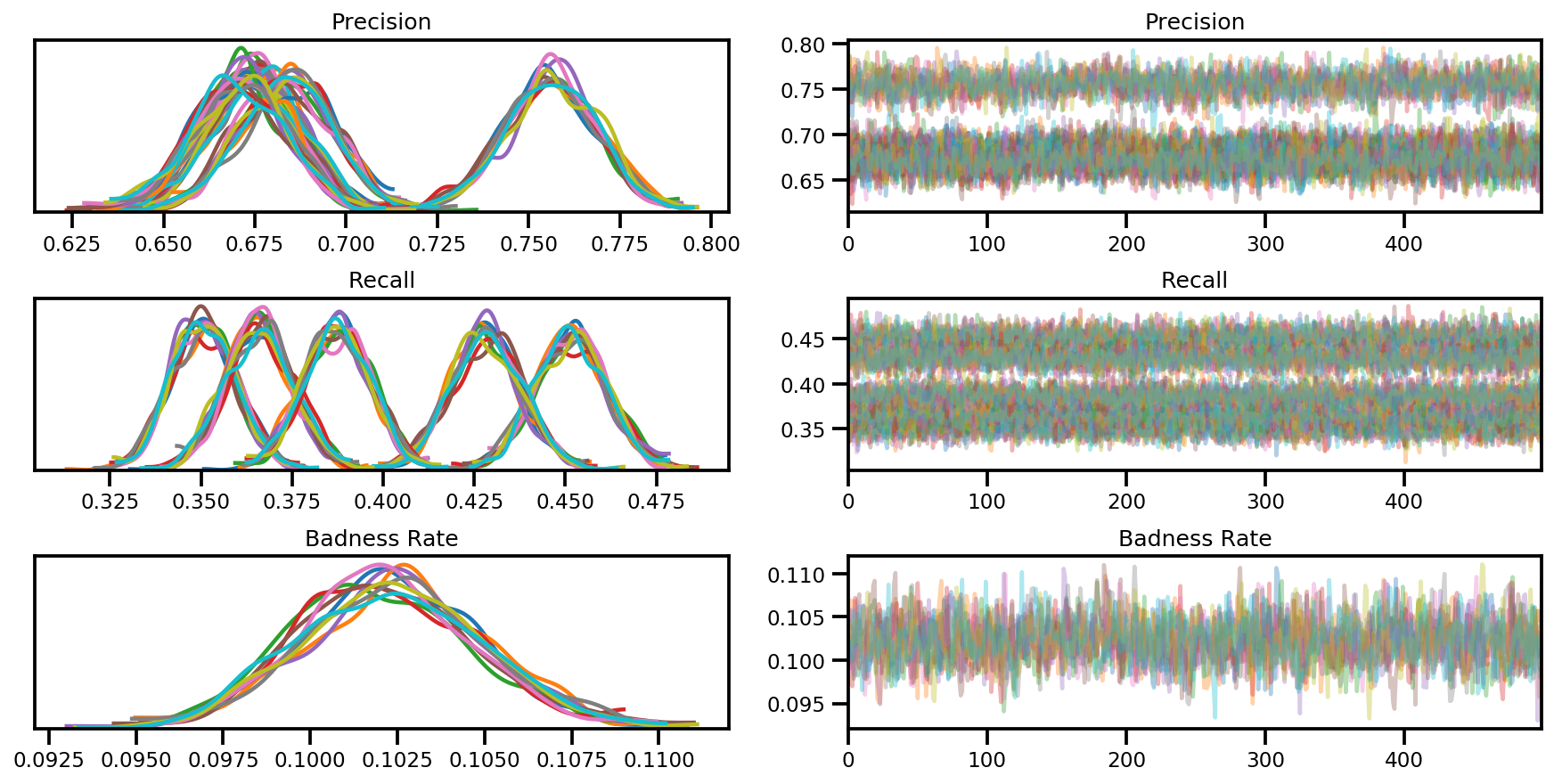
var_name = ['Precision', 'Recall', 'Badness Rate']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
axes = az.plot_trace(az_trace, compact=True);