Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
JointDistributionSequential es una distribución similar de reciente introducción clase que permite a los usuarios de prototipo rápido modelo bayesiano. Le permite encadenar varias distribuciones juntas y usar la función lambda para introducir dependencias. Está diseñado para construir modelos bayesianos de tamaño pequeño a mediano, incluidos muchos modelos de uso común como GLM, modelos de efectos mixtos, modelos de mezcla y más. Habilita todas las características necesarias para un flujo de trabajo bayesiano: muestreo predictivo previo, podría ser un complemento a otro modelo gráfico bayesiano o red neuronal más grande. En este Colab, mostraremos algunos ejemplos de cómo utilizar JointDistributionSequential para lograr su día a día bayesiano flujo de trabajo
Dependencias y requisitos previos
# We will be using ArviZ, a multi-backend Bayesian diagnosis and plotting librarypip3 install -q git+git://github.com/arviz-devs/arviz.git
Importación y configuraciones
from pprint import pprint
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import arviz as az
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
sns.reset_defaults()
#sns.set_style('whitegrid')
#sns.set_context('talk')
sns.set_context(context='talk',font_scale=0.7)
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
¡Haz las cosas rápido!
Antes de sumergirnos, asegurémonos de que estamos usando una GPU para esta demostración.
Para hacer esto, seleccione "Tiempo de ejecución" -> "Cambiar tipo de tiempo de ejecución" -> "Acelerador de hardware" -> "GPU".
El siguiente fragmento verificará que tenemos acceso a una GPU.
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
Distribución conjunta
Notas: Esta clase de distribución es útil cuando solo tiene un modelo simple. "Simple" significa gráficos en forma de cadena; aunque el enfoque funciona técnicamente para cualquier PGM con un grado como máximo de 255 para un solo nodo (porque las funciones de Python pueden tener como máximo esta cantidad de argumentos).
La idea básica es hacer que el usuario especifique una lista de los callable s que producen tfp.Distribution casos, uno para cada vértice en su PGM . El callable tendrá como máximo tantos argumentos como su índice en la lista. (Para comodidad del usuario, los datos se pasarán en orden inverso al de su creación). Internamente, "recorreremos el gráfico" simplemente pasando el valor de cada RV anterior a cada invocable. Al hacerlo, ponemos en práctica la [regla de la cadena de probablity] (https://en.wikipedia.org/wiki/Chain regla (probabilidad 29% # More_than_two_random_variables): \(p(\{x\}_i^d)=\prod_i^d p(x_i|x_{<i})\).
La idea es bastante simple, incluso como código Python. Aquí está la esencia:
# The chain rule of probability, manifest as Python code.
def log_prob(rvs, xs):
# xs[:i] is rv[i]'s markov blanket. `[::-1]` just reverses the list.
return sum(rv(*xs[i-1::-1]).log_prob(xs[i])
for i, rv in enumerate(rvs))
Puede encontrar más información de la cadena de documentación de JointDistributionSequential , pero la esencia es que se pasa una lista de distribuciones para inicializar la clase, si algunas distribuciones de la lista está dependiendo de la salida de otra distribución / variable de aguas arriba, sólo lo envuelve con una función lambda. ¡Ahora veamos cómo funciona en acción!
(Robusto) Regresión lineal
De PyMC3 doc GLM: Regresión robusta con detección de valores atípicos
Obtener datos
dfhogg = pd.DataFrame(np.array([[1, 201, 592, 61, 9, -0.84],
[2, 244, 401, 25, 4, 0.31],
[3, 47, 583, 38, 11, 0.64],
[4, 287, 402, 15, 7, -0.27],
[5, 203, 495, 21, 5, -0.33],
[6, 58, 173, 15, 9, 0.67],
[7, 210, 479, 27, 4, -0.02],
[8, 202, 504, 14, 4, -0.05],
[9, 198, 510, 30, 11, -0.84],
[10, 158, 416, 16, 7, -0.69],
[11, 165, 393, 14, 5, 0.30],
[12, 201, 442, 25, 5, -0.46],
[13, 157, 317, 52, 5, -0.03],
[14, 131, 311, 16, 6, 0.50],
[15, 166, 400, 34, 6, 0.73],
[16, 160, 337, 31, 5, -0.52],
[17, 186, 423, 42, 9, 0.90],
[18, 125, 334, 26, 8, 0.40],
[19, 218, 533, 16, 6, -0.78],
[20, 146, 344, 22, 5, -0.56]]),
columns=['id','x','y','sigma_y','sigma_x','rho_xy'])
## for convenience zero-base the 'id' and use as index
dfhogg['id'] = dfhogg['id'] - 1
dfhogg.set_index('id', inplace=True)
## standardize (mean center and divide by 1 sd)
dfhoggs = (dfhogg[['x','y']] - dfhogg[['x','y']].mean(0)) / dfhogg[['x','y']].std(0)
dfhoggs['sigma_y'] = dfhogg['sigma_y'] / dfhogg['y'].std(0)
dfhoggs['sigma_x'] = dfhogg['sigma_x'] / dfhogg['x'].std(0)
def plot_hoggs(dfhoggs):
## create xlims ylims for plotting
xlims = (dfhoggs['x'].min() - np.ptp(dfhoggs['x'])/5,
dfhoggs['x'].max() + np.ptp(dfhoggs['x'])/5)
ylims = (dfhoggs['y'].min() - np.ptp(dfhoggs['y'])/5,
dfhoggs['y'].max() + np.ptp(dfhoggs['y'])/5)
## scatterplot the standardized data
g = sns.FacetGrid(dfhoggs, size=8)
_ = g.map(plt.errorbar, 'x', 'y', 'sigma_y', 'sigma_x', marker="o", ls='')
_ = g.axes[0][0].set_ylim(ylims)
_ = g.axes[0][0].set_xlim(xlims)
plt.subplots_adjust(top=0.92)
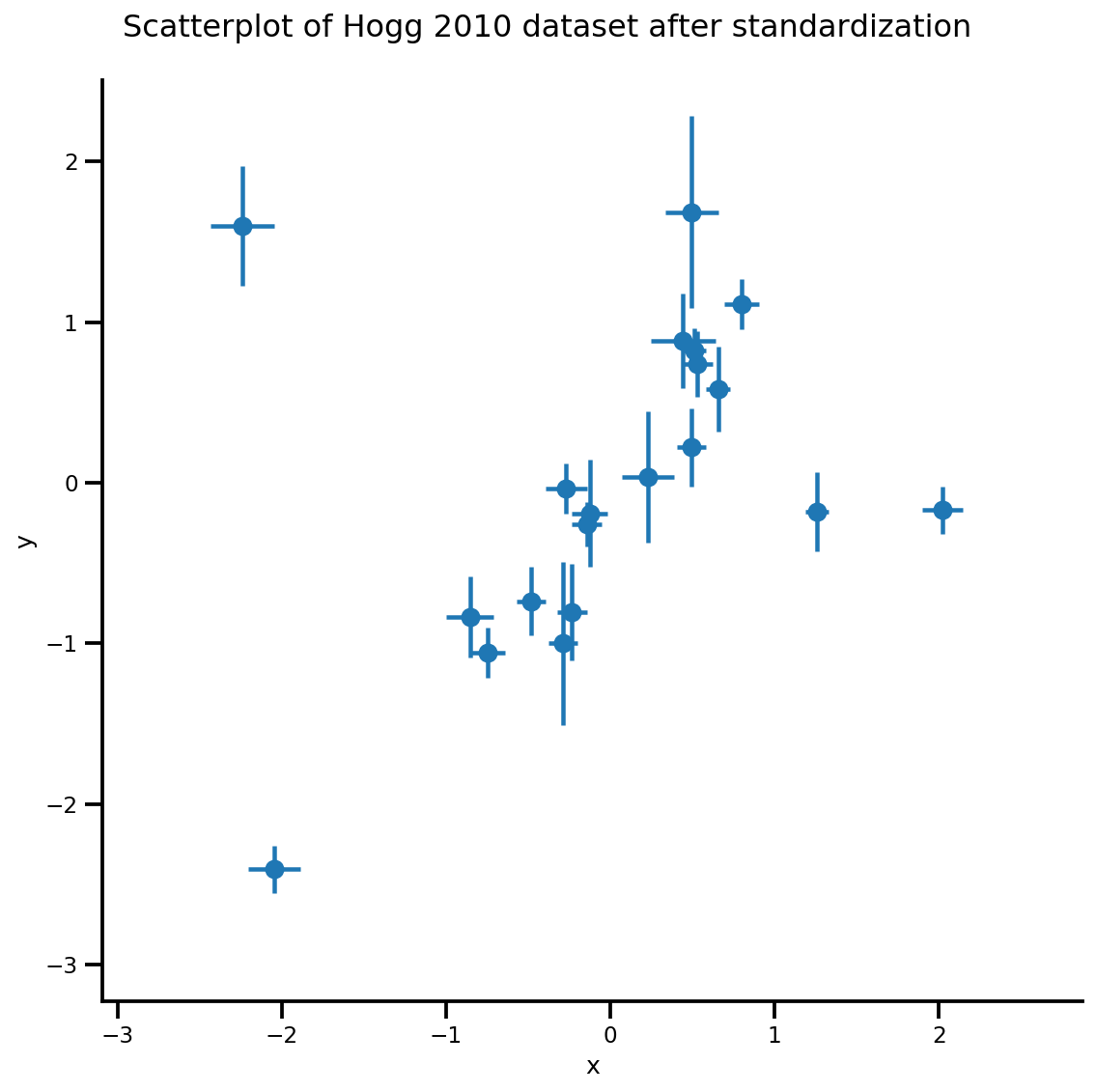
_ = g.fig.suptitle('Scatterplot of Hogg 2010 dataset after standardization', fontsize=16)
return g, xlims, ylims
g = plot_hoggs(dfhoggs)
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
X_np = dfhoggs['x'].values
sigma_y_np = dfhoggs['sigma_y'].values
Y_np = dfhoggs['y'].values
Modelo OLS convencional
Ahora, configuremos un modelo lineal, un simple problema de regresión de intersección + pendiente:
mdl_ols = tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1 ~ Normal(0, 1)
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# x ~ Normal(b0+b1*X, 1)
lambda b1, b0: tfd.Normal(
# Parameter transformation
loc=b0 + b1*X_np,
scale=sigma_y_np)
])
Luego puede verificar el gráfico del modelo para ver la dependencia. Tenga en cuenta que x está reservado como el nombre del último nodo, y usted no puede sure como su argumento lambda en su modelo JointDistributionSequential.
mdl_ols.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
El muestreo del modelo es bastante sencillo:
mdl_ols.sample()
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.50225804634794>,
<tf.Tensor: shape=(), dtype=float64, numpy=0.682740126293564>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.33051382, 0.71443618, -1.91085683, 0.89371173, -0.45060957,
-1.80448758, -0.21357082, 0.07891058, -0.20689721, -0.62690385,
-0.55225748, -0.11446535, -0.66624497, -0.86913291, -0.93605552,
-0.83965336, -0.70988597, -0.95813437, 0.15884761, -0.31113434])>]
... que da una lista de tf.Tensor. Puede conectarlo inmediatamente a la función log_prob para calcular el log_prob del modelo:
prior_predictive_samples = mdl_ols.sample()
mdl_ols.log_prob(prior_predictive_samples)
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-4.97502846, -3.98544303, -4.37514505, -3.46933487, -3.80688125,
-3.42907525, -4.03263074, -3.3646366 , -4.70370938, -4.36178501,
-3.47823735, -3.94641662, -5.76906319, -4.0944128 , -4.39310708,
-4.47713894, -4.46307881, -3.98802372, -3.83027747, -4.64777082])>
Hmmm, algo no está bien aquí: ¡deberíamos obtener un log_prob escalar! De hecho, podemos comprobar más para ver si algo está fuera llamando a los .log_prob_parts , lo que da la log_prob de cada uno de los nodos en el modelo gráfico:
mdl_ols.log_prob_parts(prior_predictive_samples)
[<tf.Tensor: shape=(), dtype=float64, numpy=-0.9699239562734849>,
<tf.Tensor: shape=(), dtype=float64, numpy=-3.459364167569284>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.54574034, 0.4438451 , 0.05414307, 0.95995326, 0.62240687,
1.00021288, 0.39665739, 1.06465152, -0.27442125, 0.06750311,
0.95105078, 0.4828715 , -1.33977506, 0.33487533, 0.03618104,
-0.04785082, -0.03379069, 0.4412644 , 0.59901066, -0.2184827 ])>]
... resulta que el último nodo no se reduce_sum a lo largo de la dimensión / eje iid. Cuando hacemos la suma, las dos primeras variables se difunden incorrectamente.
El truco aquí es usar tfd.Independent a reinterpretado la forma de lotes (para que el resto del eje se reducirá correctamente):
mdl_ols_ = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
# b1 shape: (batch_shape), X shape (num_obs): we want result to have
# shape (batch_shape, num_obs)
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
])
Ahora, verifiquemos el último nodo / distribución del modelo, puede ver que la forma del evento ahora se interpreta correctamente. Tenga en cuenta que puede ser que tome un poco de ensayo y error para obtener los reinterpreted_batch_ndims derecha, pero siempre se puede imprimir fácilmente la distribución o el tensor de la muestra a una doble comprobación de la forma!
print(mdl_ols_.sample_distributions()[0][-1])
print(mdl_ols.sample_distributions()[0][-1])
tfp.distributions.Independent("JointDistributionSequential_sample_distributions_IndependentJointDistributionSequential_sample_distributions_Normal", batch_shape=[], event_shape=[20], dtype=float64)
tfp.distributions.Normal("JointDistributionSequential_sample_distributions_Normal", batch_shape=[20], event_shape=[], dtype=float64)
prior_predictive_samples = mdl_ols_.sample()
mdl_ols_.log_prob(prior_predictive_samples) # <== Getting a scalar correctly
<tf.Tensor: shape=(), dtype=float64, numpy=-2.543425661013286>
Otro JointDistribution* API
mdl_ols_named = tfd.JointDistributionNamed(dict(
likelihood = lambda b0, b1: tfd.Independent(
tfd.Normal(
loc=b0 + b1*X_np,
scale=sigma_y_np),
reinterpreted_batch_ndims=1
),
b0 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
b1 = tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
))
mdl_ols_named.log_prob(mdl_ols_named.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-5.99620966071338>
mdl_ols_named.sample() # output is a dictionary
{'b0': <tf.Tensor: shape=(), dtype=float64, numpy=0.26364058399428225>,
'b1': <tf.Tensor: shape=(), dtype=float64, numpy=-0.27209402374432207>,
'likelihood': <tf.Tensor: shape=(20,), dtype=float64, numpy=
array([ 0.6482155 , -0.39314108, 0.62744764, -0.24587987, -0.20544617,
1.01465392, -0.04705611, -0.16618702, 0.36410134, 0.3943299 ,
0.36455291, -0.27822219, -0.24423928, 0.24599518, 0.82731092,
-0.21983033, 0.56753169, 0.32830481, -0.15713064, 0.23336351])>}
Root = tfd.JointDistributionCoroutine.Root # Convenient alias.
def model():
b1 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
b0 = yield Root(tfd.Normal(loc=tf.cast(0, dtype), scale=1.))
yhat = b0 + b1*X_np
likelihood = yield tfd.Independent(
tfd.Normal(loc=yhat, scale=sigma_y_np),
reinterpreted_batch_ndims=1
)
mdl_ols_coroutine = tfd.JointDistributionCoroutine(model)
mdl_ols_coroutine.log_prob(mdl_ols_coroutine.sample())
<tf.Tensor: shape=(), dtype=float64, numpy=-4.566678123520463>
mdl_ols_coroutine.sample() # output is a tuple
(<tf.Tensor: shape=(), dtype=float64, numpy=0.06811002171170354>,
<tf.Tensor: shape=(), dtype=float64, numpy=-0.37477064754116807>,
<tf.Tensor: shape=(20,), dtype=float64, numpy=
array([-0.91615096, -0.20244718, -0.47840159, -0.26632479, -0.60441105,
-0.48977789, -0.32422329, -0.44019322, -0.17072643, -0.20666025,
-0.55932191, -0.40801868, -0.66893181, -0.24134135, -0.50403536,
-0.51788596, -0.90071876, -0.47382338, -0.34821655, -0.38559724])>)
MLE
¡Y ahora podemos hacer inferencias! Puede utilizar el optimizador para encontrar la estimación de máxima verosimilitud.
Definir algunas funciones auxiliares
# bfgs and lbfgs currently requries a function that returns both the value and
# gradient re the input.
import functools
def _make_val_and_grad_fn(value_fn):
@functools.wraps(value_fn)
def val_and_grad(x):
return tfp.math.value_and_gradient(value_fn, x)
return val_and_grad
# Map a list of tensors (e.g., output from JDSeq.sample([...])) to a single tensor
# modify from tfd.Blockwise
from tensorflow_probability.python.internal import dtype_util
from tensorflow_probability.python.internal import prefer_static as ps
from tensorflow_probability.python.internal import tensorshape_util
class Mapper:
"""Basically, this is a bijector without log-jacobian correction."""
def __init__(self, list_of_tensors, list_of_bijectors, event_shape):
self.dtype = dtype_util.common_dtype(
list_of_tensors, dtype_hint=tf.float32)
self.list_of_tensors = list_of_tensors
self.bijectors = list_of_bijectors
self.event_shape = event_shape
def flatten_and_concat(self, list_of_tensors):
def _reshape_map_part(part, event_shape, bijector):
part = tf.cast(bijector.inverse(part), self.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([
ps.shape(part)[:ps.size(ps.shape(part)) - ps.size(event_shape)],
[-1]
], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
list_of_tensors,
self.event_shape,
self.bijectors)
return tf.concat(tf.nest.flatten(x), axis=-1)
def split_and_reshape(self, x):
assertions = []
message = 'Input must have at least one dimension.'
if tensorshape_util.rank(x.shape) is not None:
if tensorshape_util.rank(x.shape) == 0:
raise ValueError(message)
else:
assertions.append(assert_util.assert_rank_at_least(x, 1, message=message))
with tf.control_dependencies(assertions):
splits = [
tf.cast(ps.maximum(1, ps.reduce_prod(s)), tf.int32)
for s in tf.nest.flatten(self.event_shape)
]
x = tf.nest.pack_sequence_as(
self.event_shape, tf.split(x, splits, axis=-1))
def _reshape_map_part(part, part_org, event_shape, bijector):
part = tf.cast(bijector.forward(part), part_org.dtype)
static_rank = tf.get_static_value(ps.rank_from_shape(event_shape))
if static_rank == 1:
return part
new_shape = ps.concat([ps.shape(part)[:-1], event_shape], axis=-1)
return tf.reshape(part, ps.cast(new_shape, tf.int32))
x = tf.nest.map_structure(_reshape_map_part,
x,
self.list_of_tensors,
self.event_shape,
self.bijectors)
return x
mapper = Mapper(mdl_ols_.sample()[:-1],
[tfb.Identity(), tfb.Identity()],
mdl_ols_.event_shape[:-1])
# mapper.split_and_reshape(mapper.flatten_and_concat(mdl_ols_.sample()[:-1]))
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input.
return -mdl_ols_.log_prob(mapper.split_and_reshape(x) + [Y_np])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=tf.zeros(2, dtype=dtype),
tolerance=1e-20,
x_tolerance=1e-8
)
b0est, b1est = lbfgs_results.position.numpy()
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
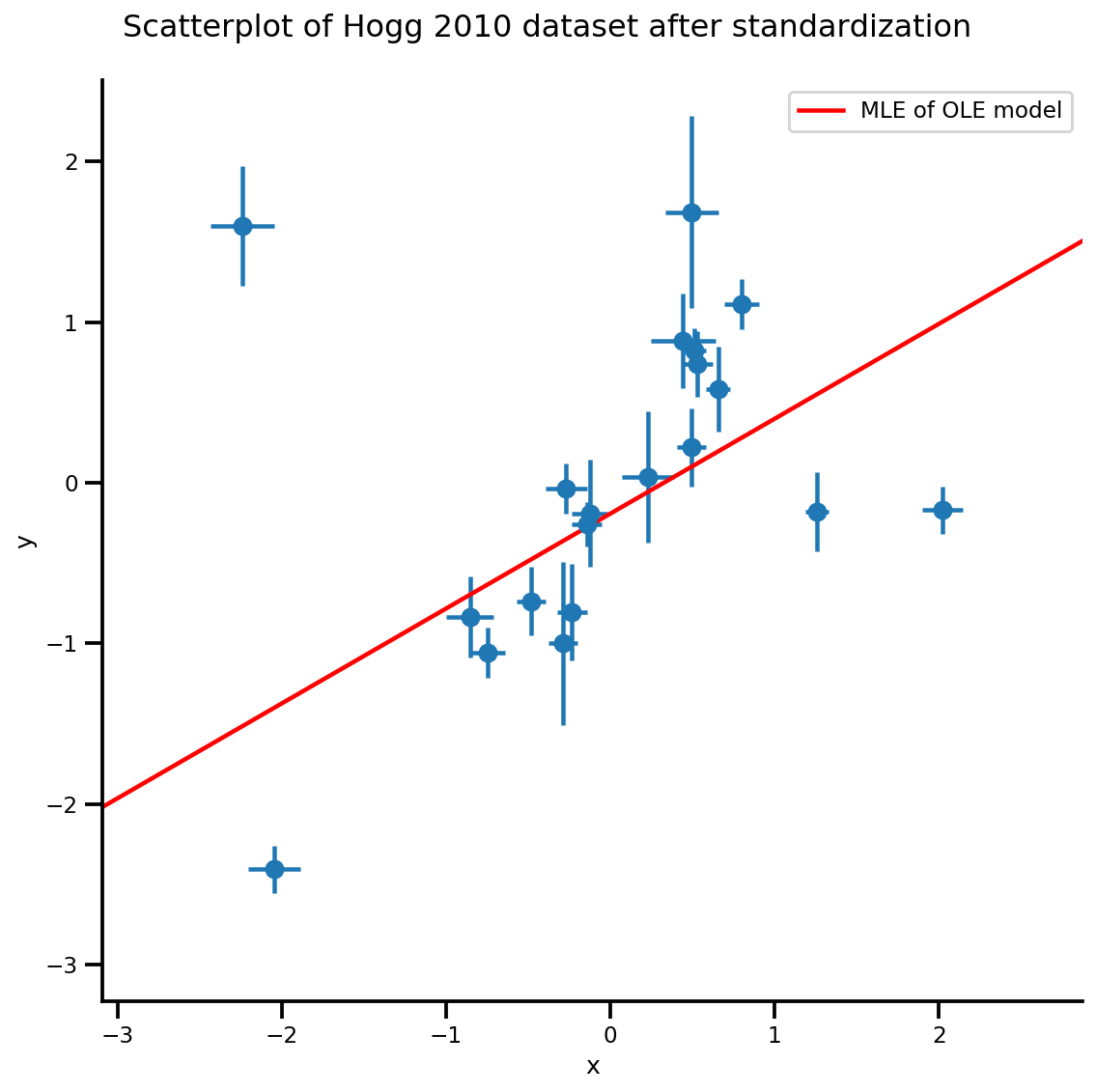
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of OLE model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
Modelo de versión por lotes y MCMC
En inferencia bayesiana, que por lo general quieren trabajar con muestras MCMC, como cuando las muestras son de la parte posterior, que puede conectarlos a cualquier función de las expectativas de cómputo. Sin embargo, la API MCMC nos obligan a escribir modelos que están por lotes amable, y podemos comprobar que nuestro modelo no es en realidad "procesable por lotes" llamando sample([...])
mdl_ols_.sample(5) # <== error as some computation could not be broadcasted.
En este caso, es relativamente sencillo ya que solo tenemos una función lineal dentro de nuestro modelo, expandir la forma debería funcionar:
mdl_ols_batch = tfd.JointDistributionSequential([
# b0
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# b1
tfd.Normal(loc=tf.cast(0, dtype), scale=1.),
# likelihood
# Using Independent to ensure the log_prob is not incorrectly broadcasted
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0[..., tf.newaxis] + b1[..., tf.newaxis]*X_np[tf.newaxis, ...],
scale=sigma_y_np[tf.newaxis, ...]),
reinterpreted_batch_ndims=1
),
])
mdl_ols_batch.resolve_graph()
(('b0', ()), ('b1', ()), ('x', ('b1', 'b0')))
Podemos volver a muestrear y evaluar log_prob_parts para hacer algunas comprobaciones:
b0, b1, y = mdl_ols_batch.sample(4)
mdl_ols_batch.log_prob_parts([b0, b1, y])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.25230168, -1.45281432, -1.87110061, -1.07665206])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.07019936, -1.59562117, -2.53387765, -1.01557632])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.45841406, 2.56829635, -4.84973951, -5.59423992])>]
Algunas notas al margen:
- Queremos trabajar con la versión por lotes del modelo porque es la más rápida para MCMC multicadena. En los casos en que no se puede reescribir el modelo como una versión por lotes (por ejemplo, modelos ODE), puede asignar la función log_prob usando
tf.map_fnpara lograr el mismo efecto. - Ahora
mdl_ols_batch.sample()puede que no funcione como hemos escalador antes, ya que no podemos hacerscaler_tensor[:, None]. Aquí la solución es ampliar tensor de escalador a la fila 1 por envolturatfd.Sample(..., sample_shape=1). - Es una buena práctica escribir el modelo como una función para que pueda cambiar configuraciones como hiperparámetros mucho más fácilmente.
def gen_ols_batch_model(X, sigma, hyperprior_mean=0, hyperprior_scale=1):
hyper_mean = tf.cast(hyperprior_mean, dtype)
hyper_scale = tf.cast(hyperprior_scale, dtype)
return tfd.JointDistributionSequential([
# b0
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# b1
tfd.Sample(tfd.Normal(loc=hyper_mean, scale=hyper_scale), sample_shape=1),
# likelihood
lambda b1, b0: tfd.Independent(
tfd.Normal(
# Parameter transformation
loc=b0 + b1*X,
scale=sigma),
reinterpreted_batch_ndims=1
),
], validate_args=True)
mdl_ols_batch = gen_ols_batch_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
_ = mdl_ols_batch.sample()
_ = mdl_ols_batch.sample(4)
_ = mdl_ols_batch.sample([3, 4])
# Small helper function to validate log_prob shape (avoid wrong broadcasting)
def validate_log_prob_part(model, batch_shape=1, observed=-1):
samples = model.sample(batch_shape)
logp_part = list(model.log_prob_parts(samples))
# exclude observed node
logp_part.pop(observed)
for part in logp_part:
tf.assert_equal(part.shape, logp_part[-1].shape)
validate_log_prob_part(mdl_ols_batch, 4)
Más comprobaciones: comparar la función log_prob generada con la función log_prob de TFP manuscrita.
def ols_logp_batch(b0, b1, Y):
b0_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b0
b1_prior = tfd.Normal(loc=tf.cast(0, dtype), scale=1.) # b1
likelihood = tfd.Normal(loc=b0 + b1*X_np[None, :],
scale=sigma_y_np) # likelihood
return tf.reduce_sum(b0_prior.log_prob(b0), axis=-1) +\
tf.reduce_sum(b1_prior.log_prob(b1), axis=-1) +\
tf.reduce_sum(likelihood.log_prob(Y), axis=-1)
b0, b1, x = mdl_ols_batch.sample(4)
print(mdl_ols_batch.log_prob([b0, b1, Y_np]).numpy())
print(ols_logp_batch(b0, b1, Y_np).numpy())
[-227.37899384 -327.10043743 -570.44162789 -702.79808683] [-227.37899384 -327.10043743 -570.44162789 -702.79808683]
MCMC usando el muestreador sin giro en U
Un común run_chain función
@tf.function(autograph=False, experimental_compile=True)
def run_chain(init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
num_steps=500, burnin=50):
def trace_fn(_, pkr):
return (
pkr.inner_results.inner_results.target_log_prob,
pkr.inner_results.inner_results.leapfrogs_taken,
pkr.inner_results.inner_results.has_divergence,
pkr.inner_results.inner_results.energy,
pkr.inner_results.inner_results.log_accept_ratio
)
kernel = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.NoUTurnSampler(
target_log_prob_fn,
step_size=step_size),
bijector=unconstraining_bijectors)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=kernel,
num_adaptation_steps=burnin,
step_size_setter_fn=lambda pkr, new_step_size: pkr._replace(
inner_results=pkr.inner_results._replace(step_size=new_step_size)),
step_size_getter_fn=lambda pkr: pkr.inner_results.step_size,
log_accept_prob_getter_fn=lambda pkr: pkr.inner_results.log_accept_ratio
)
# Sampling from the chain.
chain_state, sampler_stat = tfp.mcmc.sample_chain(
num_results=num_steps,
num_burnin_steps=burnin,
current_state=init_state,
kernel=hmc,
trace_fn=trace_fn)
return chain_state, sampler_stat
nchain = 10
b0, b1, _ = mdl_ols_batch.sample(nchain)
init_state = [b0, b1]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1]]
target_log_prob_fn = lambda *x: mdl_ols_batch.log_prob(x + (Y_np, ))
# bijector to map contrained parameters to real
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
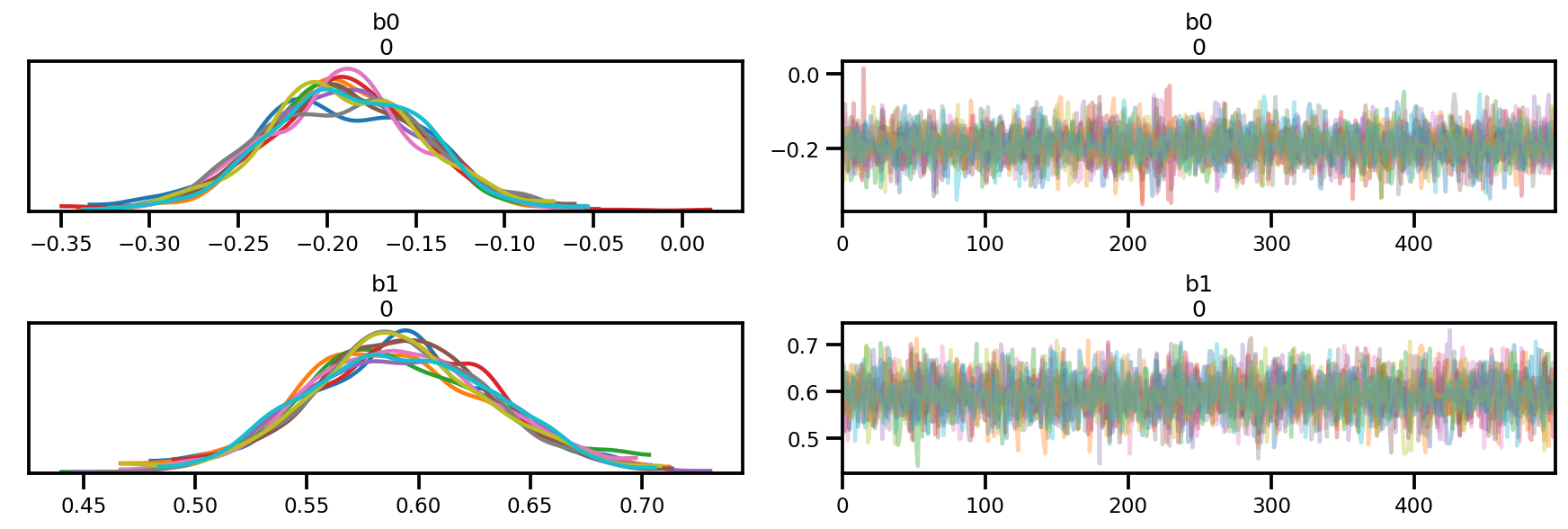
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.plot_trace(az_trace);
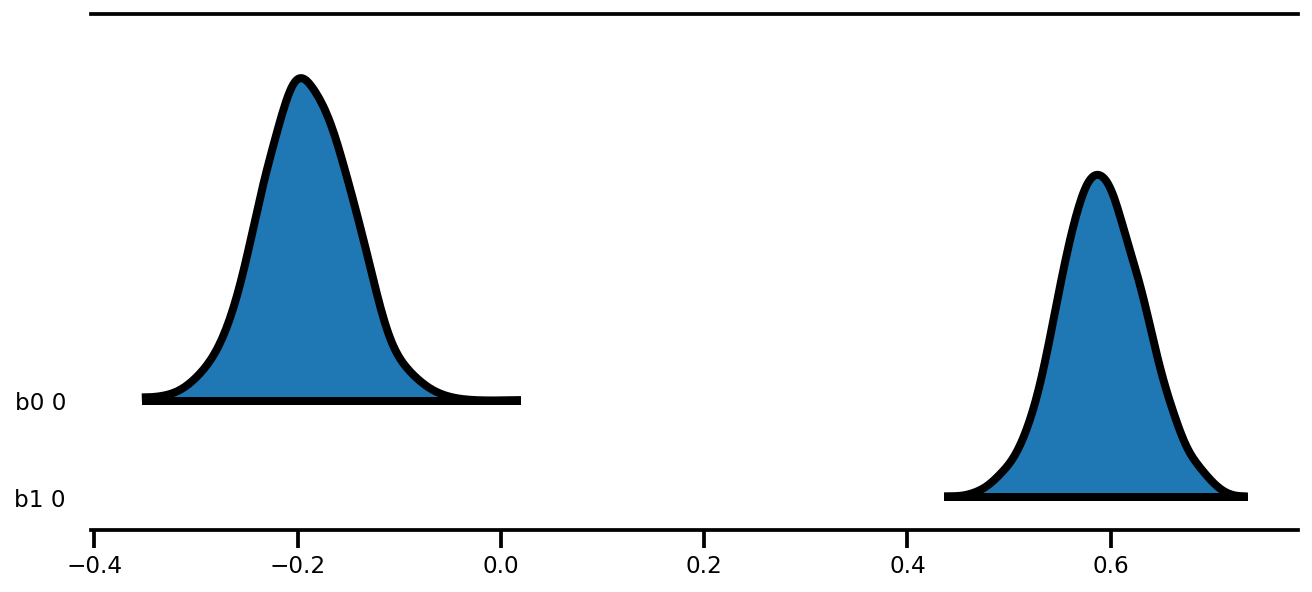
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
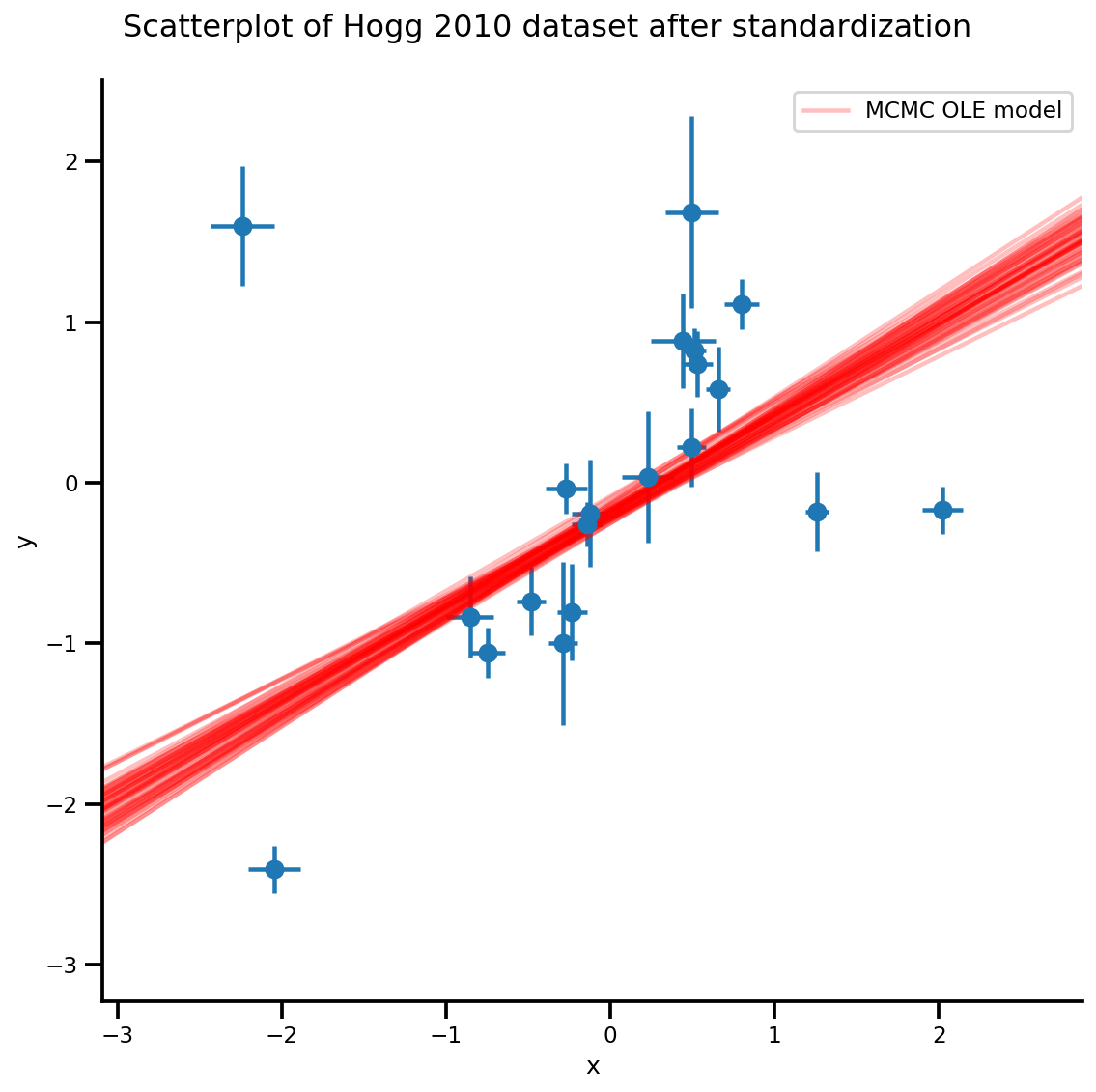
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC OLE model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Método Student-T
Tenga en cuenta que a partir de ahora siempre trabajamos con la versión por lotes de un modelo.
def gen_studentt_model(X, sigma,
hyper_mean=0, hyper_scale=1, lower=1, upper=100):
loc = tf.cast(hyper_mean, dtype)
scale = tf.cast(hyper_scale, dtype)
low = tf.cast(lower, dtype)
high = tf.cast(upper, dtype)
return tfd.JointDistributionSequential([
# b0 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# b1 ~ Normal(0, 1)
tfd.Sample(tfd.Normal(loc, scale), sample_shape=1),
# df ~ Uniform(a, b)
tfd.Sample(tfd.Uniform(low, high), sample_shape=1),
# likelihood ~ StudentT(df, f(b0, b1), sigma_y)
# Using Independent to ensure the log_prob is not incorrectly broadcasted.
lambda df, b1, b0: tfd.Independent(
tfd.StudentT(df=df, loc=b0 + b1*X, scale=sigma)),
], validate_args=True)
mdl_studentt = gen_studentt_model(X_np[tf.newaxis, ...],
sigma_y_np[tf.newaxis, ...])
mdl_studentt.resolve_graph()
(('b0', ()), ('b1', ()), ('df', ()), ('x', ('df', 'b1', 'b0')))
validate_log_prob_part(mdl_studentt, 4)
Muestra directa (muestreo predictivo previo)
b0, b1, df, x = mdl_studentt.sample(1000)
x.shape
TensorShape([1000, 20])
MLE
# bijector to map contrained parameters to real
a, b = tf.constant(1., dtype), tf.constant(100., dtype),
# Interval transformation
tfp_interval = tfb.Inline(
inverse_fn=(
lambda x: tf.math.log(x - a) - tf.math.log(b - x)),
forward_fn=(
lambda y: (b - a) * tf.sigmoid(y) + a),
forward_log_det_jacobian_fn=(
lambda x: tf.math.log(b - a) - 2 * tf.nn.softplus(-x) - x),
forward_min_event_ndims=0,
name="interval")
unconstraining_bijectors = [
tfb.Identity(),
tfb.Identity(),
tfp_interval,
]
mapper = Mapper(mdl_studentt.sample()[:-1],
unconstraining_bijectors,
mdl_studentt.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
# Generate a function closure so that we are computing the log_prob
# conditioned on the observed data. Note also that tfp.optimizer.* takes a
# single tensor as input, so we need to do some slicing here:
return -tf.squeeze(mdl_studentt.log_prob(
mapper.split_and_reshape(x) + [Y_np]))
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
initial_position=mapper.flatten_and_concat(mdl_studentt.sample()[:-1]),
tolerance=1e-20,
x_tolerance=1e-20
)
b0est, b1est, dfest = lbfgs_results.position.numpy()
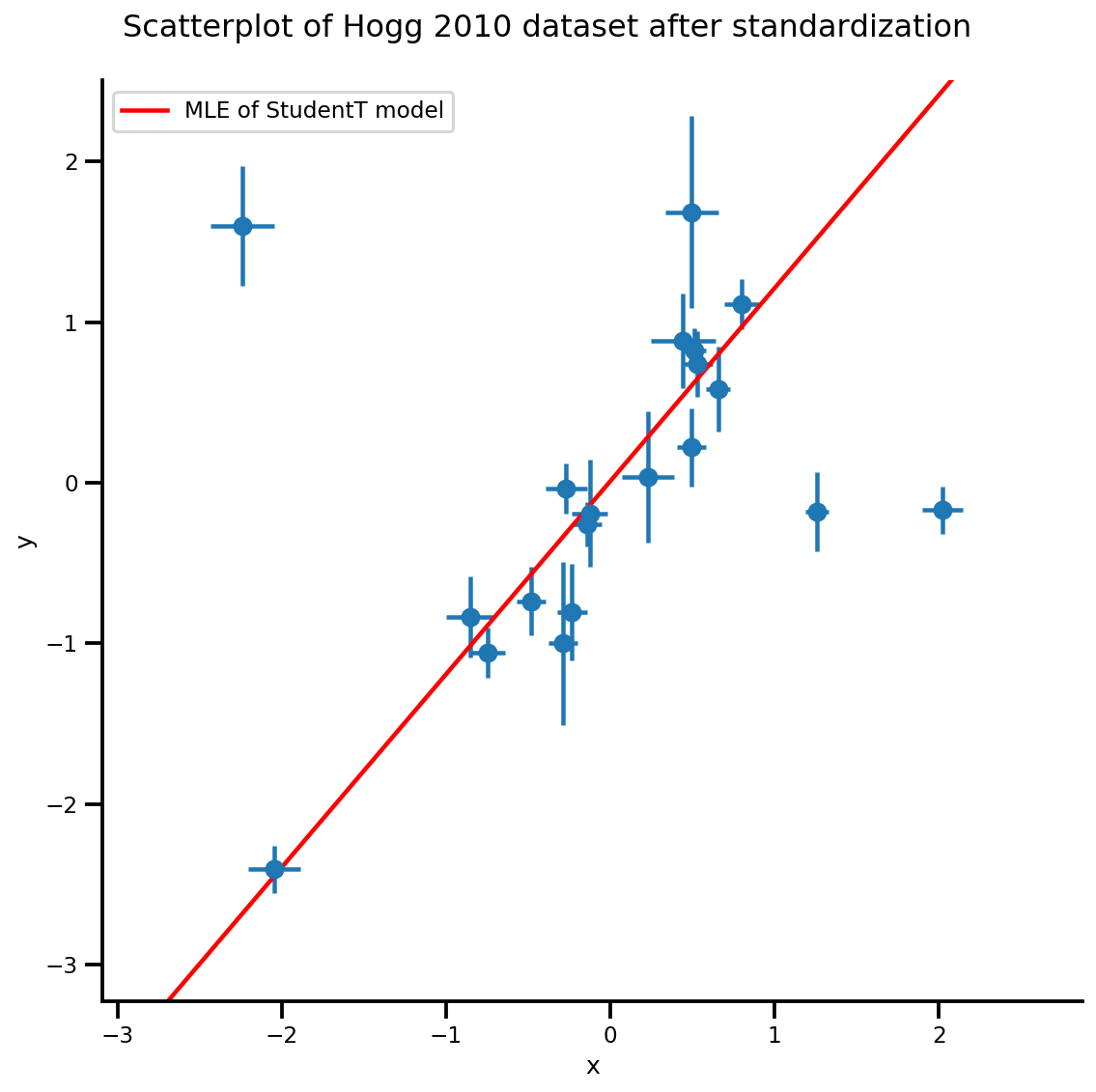
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)
g.axes[0][0].plot(xrange, b0est + b1est*xrange,
color='r', label='MLE of StudentT model')
plt.legend();
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning)
MCMC
nchain = 10
b0, b1, df, _ = mdl_studentt.sample(nchain)
init_state = [b0, b1, df]
step_size = [tf.cast(i, dtype=dtype) for i in [.1, .1, .05]]
target_log_prob_fn = lambda *x: mdl_studentt.log_prob(x + (Y_np, ))
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['b0', 'b1', 'df']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
az.summary(az_trace)
az.plot_trace(az_trace);
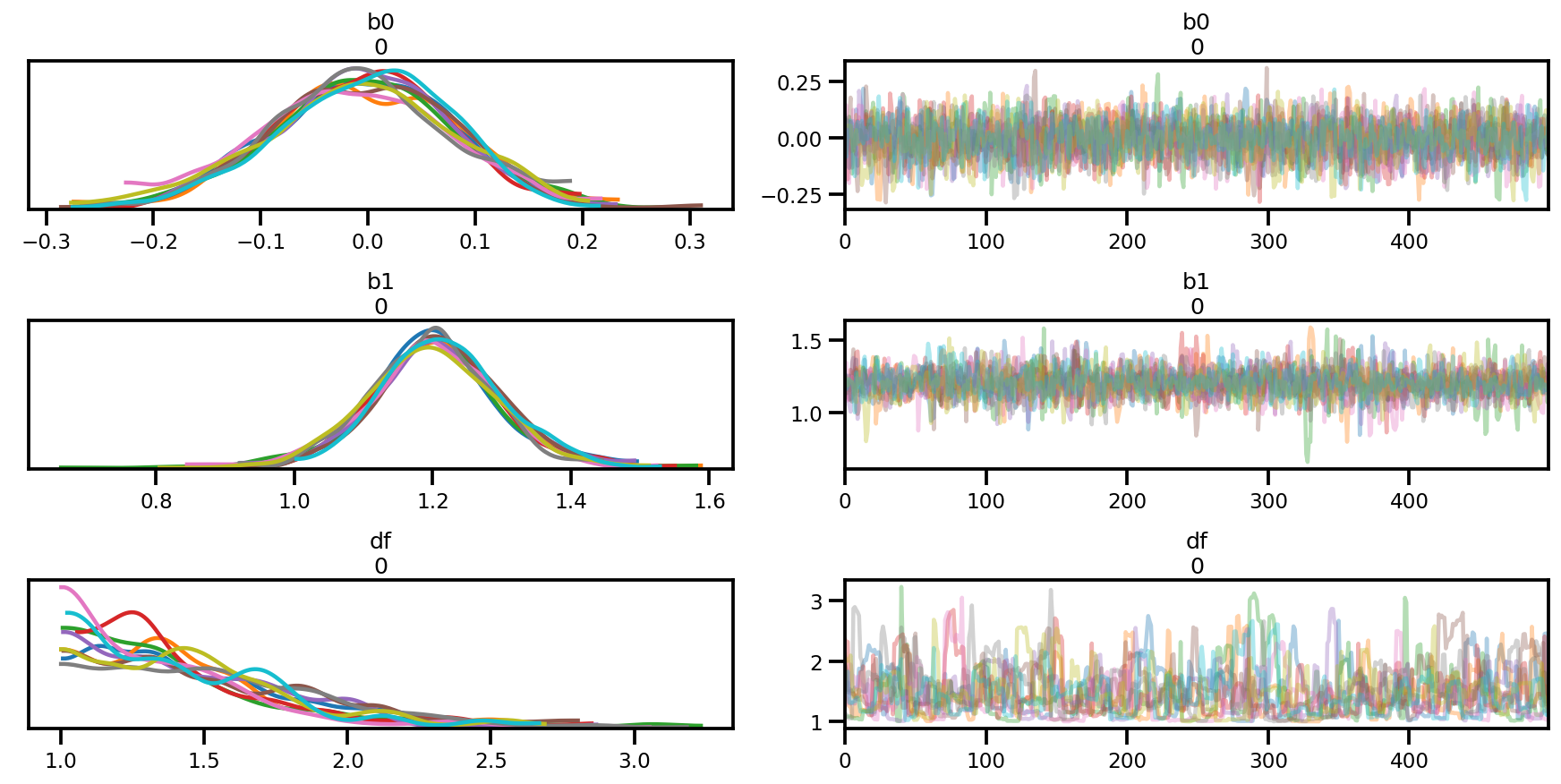
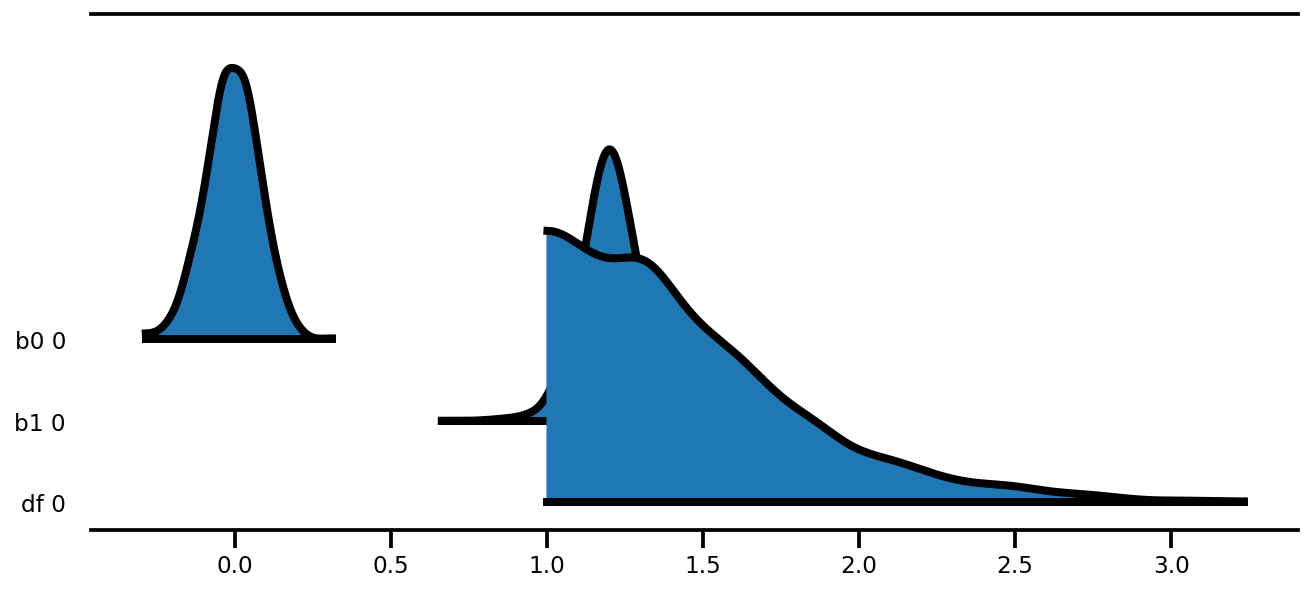
az.plot_forest(az_trace,
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 4));
plt.hist(az_trace.sample_stats['tree_size'], np.linspace(.5, 25.5, 26), alpha=.5);
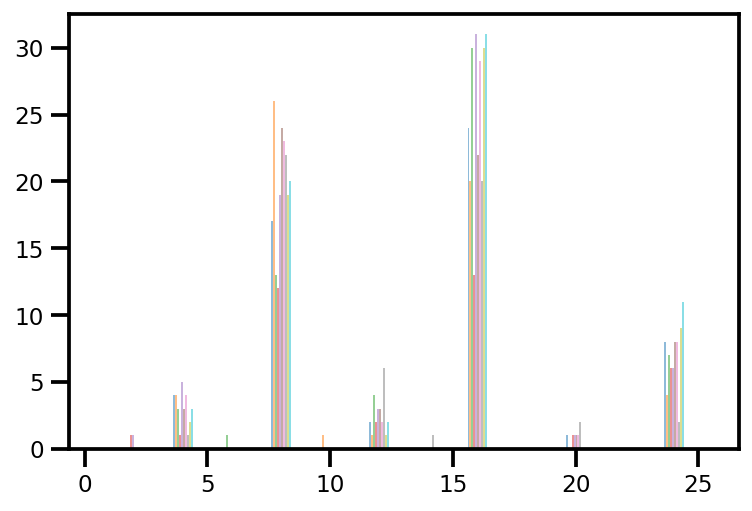
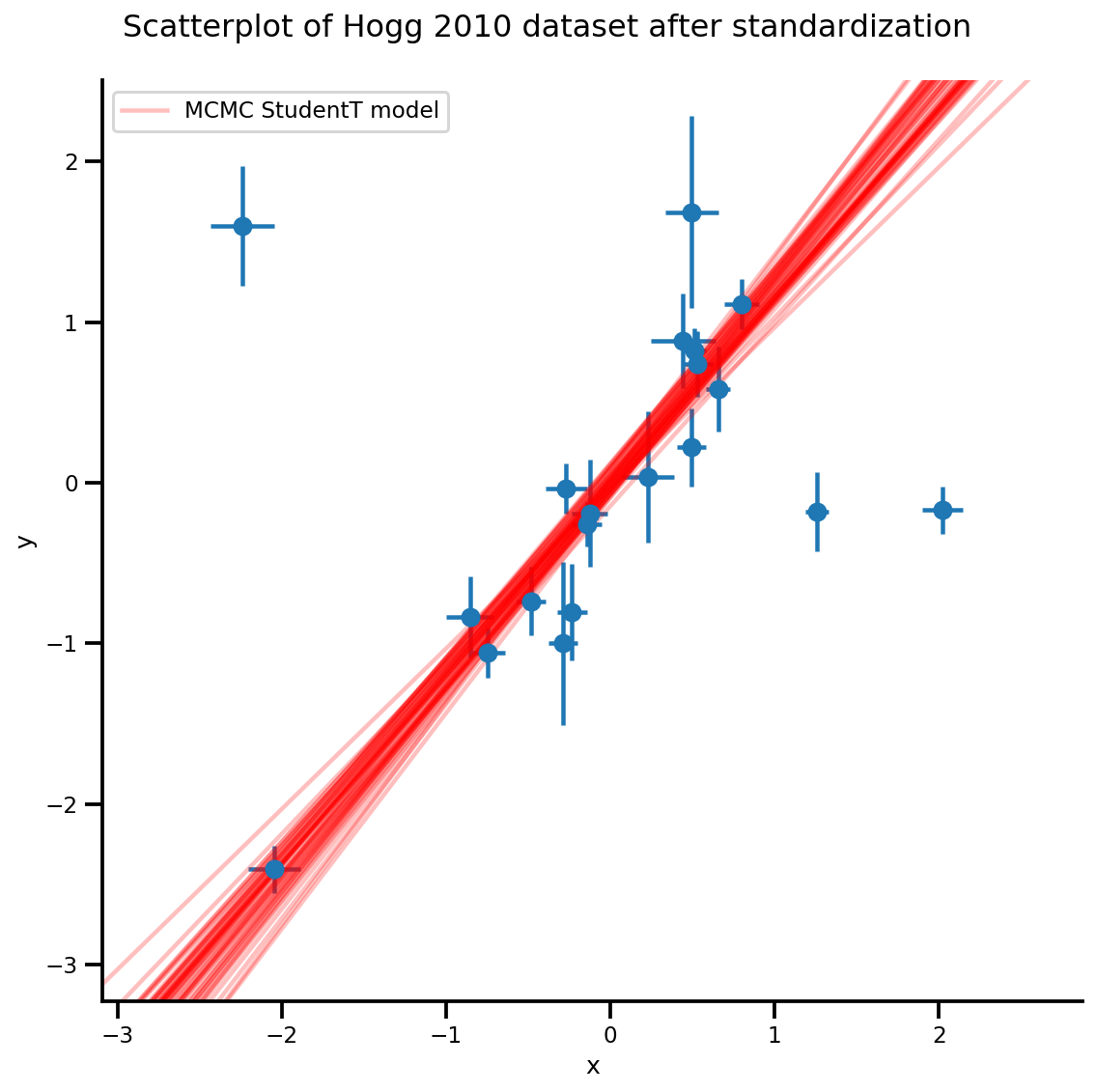
k = 5
b0est, b1est = az_trace.posterior['b0'][:, -k:].values, az_trace.posterior['b1'][:, -k:].values
g, xlims, ylims = plot_hoggs(dfhoggs);
xrange = np.linspace(xlims[0], xlims[1], 100)[None, :]
g.axes[0][0].plot(np.tile(xrange, (k, 1)).T,
(np.reshape(b0est, [-1, 1]) + np.reshape(b1est, [-1, 1])*xrange).T,
alpha=.25, color='r')
plt.legend([g.axes[0][0].lines[-1]], ['MCMC StudentT model']);
/usr/local/lib/python3.6/dist-packages/numpy/core/fromnumeric.py:2495: FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead. return ptp(axis=axis, out=out, **kwargs) /usr/local/lib/python3.6/dist-packages/seaborn/axisgrid.py:230: UserWarning: The `size` paramter has been renamed to `height`; please update your code. warnings.warn(msg, UserWarning) /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:8: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.
Agrupación parcial jerárquica
De PyMC3 datos de béisbol para jugadores de 18 Efron y Morris (1975)
data = pd.read_table('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/efron-morris-75-data.tsv',
sep="\t")
at_bats, hits = data[['At-Bats', 'Hits']].values.T
n = len(at_bats)
def gen_baseball_model(at_bats, rate=1.5, a=0, b=1):
return tfd.JointDistributionSequential([
# phi
tfd.Uniform(low=tf.cast(a, dtype), high=tf.cast(b, dtype)),
# kappa_log
tfd.Exponential(rate=tf.cast(rate, dtype)),
# thetas
lambda kappa_log, phi: tfd.Sample(
tfd.Beta(
concentration1=tf.exp(kappa_log)*phi,
concentration0=tf.exp(kappa_log)*(1.0-phi)),
sample_shape=n
),
# likelihood
lambda thetas: tfd.Independent(
tfd.Binomial(
total_count=tf.cast(at_bats, dtype),
probs=thetas
)),
])
mdl_baseball = gen_baseball_model(at_bats)
mdl_baseball.resolve_graph()
(('phi', ()),
('kappa_log', ()),
('thetas', ('kappa_log', 'phi')),
('x', ('thetas',)))
Muestra directa (muestreo predictivo previo)
phi, kappa_log, thetas, y = mdl_baseball.sample(4)
# phi, kappa_log, thetas, y
Nuevamente, observe cómo si no usa Independent, terminará con log_prob que tiene una forma de lote incorrecta.
# check logp
pprint(mdl_baseball.log_prob_parts([phi, kappa_log, thetas, hits]))
print(mdl_baseball.log_prob([phi, kappa_log, thetas, hits]))
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([0., 0., 0., 0.])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([ 0.1721297 , -0.95946498, -0.72591188, 0.23993813])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([59.35192283, 7.0650634 , 0.83744911, 74.14370935])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3279.75191016, -931.10438484, -512.59197688, -1131.08043597])>] tf.Tensor([-3220.22785762 -924.99878641 -512.48043966 -1056.69678849], shape=(4,), dtype=float64)
MLE
Una característica bastante sorprendente de tfp.optimizer es que, puede optimizado en paralelo para k lote de punto de partida y especificar el stopping_condition kwarg: se puede establecer a tfp.optimizer.converged_all para ver si todos buscan el mismo mínimo, o tfp.optimizer.converged_any para encontrar una solución local rápida.
unconstraining_bijectors = [
tfb.Sigmoid(),
tfb.Exp(),
tfb.Sigmoid(),
]
phi, kappa_log, thetas, y = mdl_baseball.sample(10)
mapper = Mapper([phi, kappa_log, thetas],
unconstraining_bijectors,
mdl_baseball.event_shape[:-1])
@_make_val_and_grad_fn
def neg_log_likelihood(x):
return -mdl_baseball.log_prob(mapper.split_and_reshape(x) + [hits])
start = mapper.flatten_and_concat([phi, kappa_log, thetas])
lbfgs_results = tfp.optimizer.lbfgs_minimize(
neg_log_likelihood,
num_correction_pairs=10,
initial_position=start,
# lbfgs actually can work in batch as well
stopping_condition=tfp.optimizer.converged_any,
tolerance=1e-50,
x_tolerance=1e-50,
parallel_iterations=10,
max_iterations=200
)
lbfgs_results.converged.numpy(), lbfgs_results.failed.numpy()
(array([False, False, False, False, False, False, False, False, False,
False]),
array([ True, True, True, True, True, True, True, True, True,
True]))
result = lbfgs_results.position[lbfgs_results.converged & ~lbfgs_results.failed]
result
<tf.Tensor: shape=(0, 20), dtype=float64, numpy=array([], shape=(0, 20), dtype=float64)>
LBFGS no convergió.
if result.shape[0] > 0:
phi_est, kappa_est, theta_est = mapper.split_and_reshape(result)
phi_est, kappa_est, theta_est
MCMC
target_log_prob_fn = lambda *x: mdl_baseball.log_prob(x + (hits, ))
nchain = 4
phi, kappa_log, thetas, _ = mdl_baseball.sample(nchain)
init_state = [phi, kappa_log, thetas]
step_size=[tf.cast(i, dtype=dtype) for i in [.1, .1, .1]]
samples, sampler_stat = run_chain(
init_state, step_size, target_log_prob_fn, unconstraining_bijectors,
burnin=200)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
var_name = ['phi', 'kappa_log', 'thetas']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
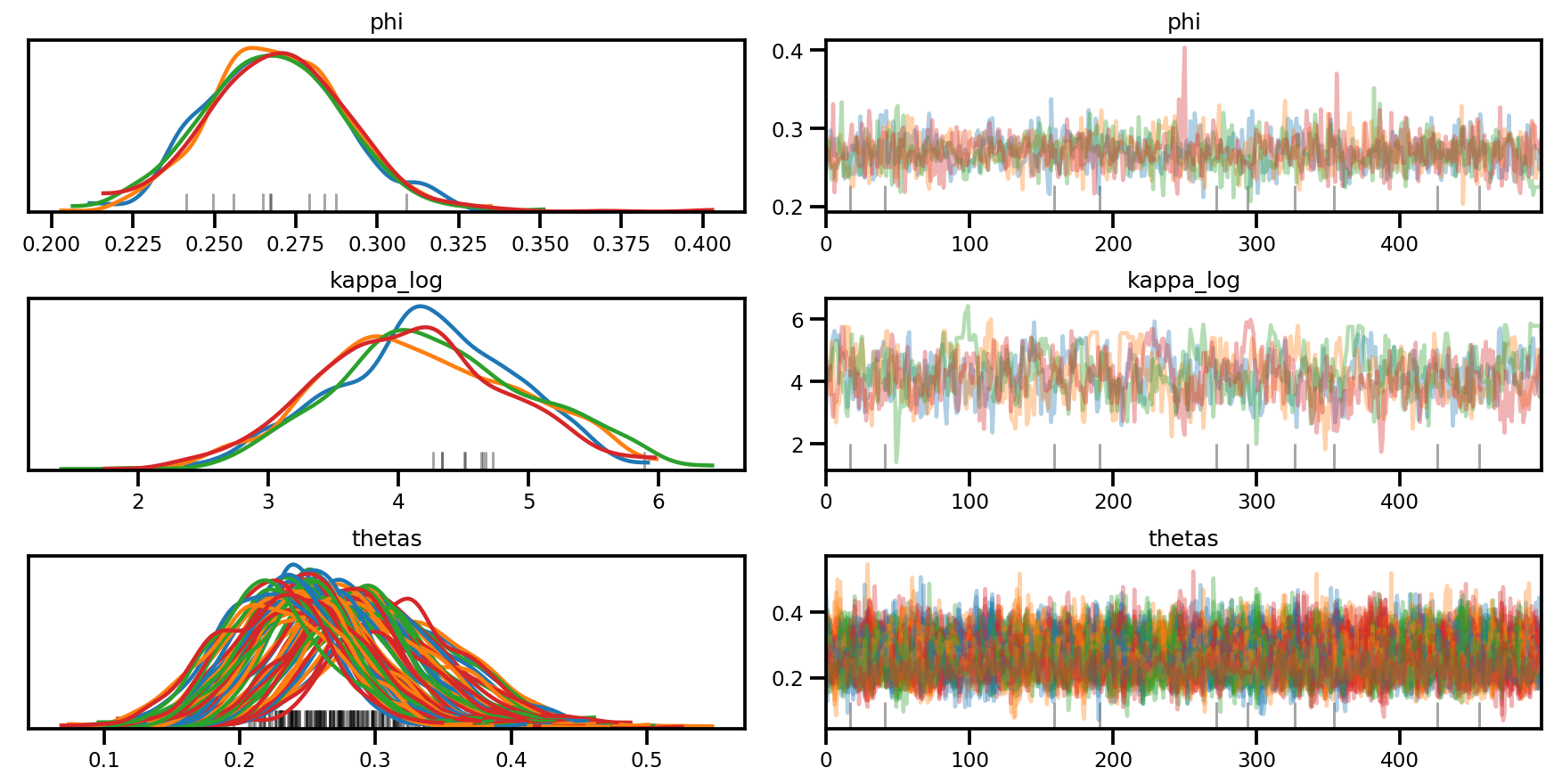
az.plot_trace(az_trace, compact=True);
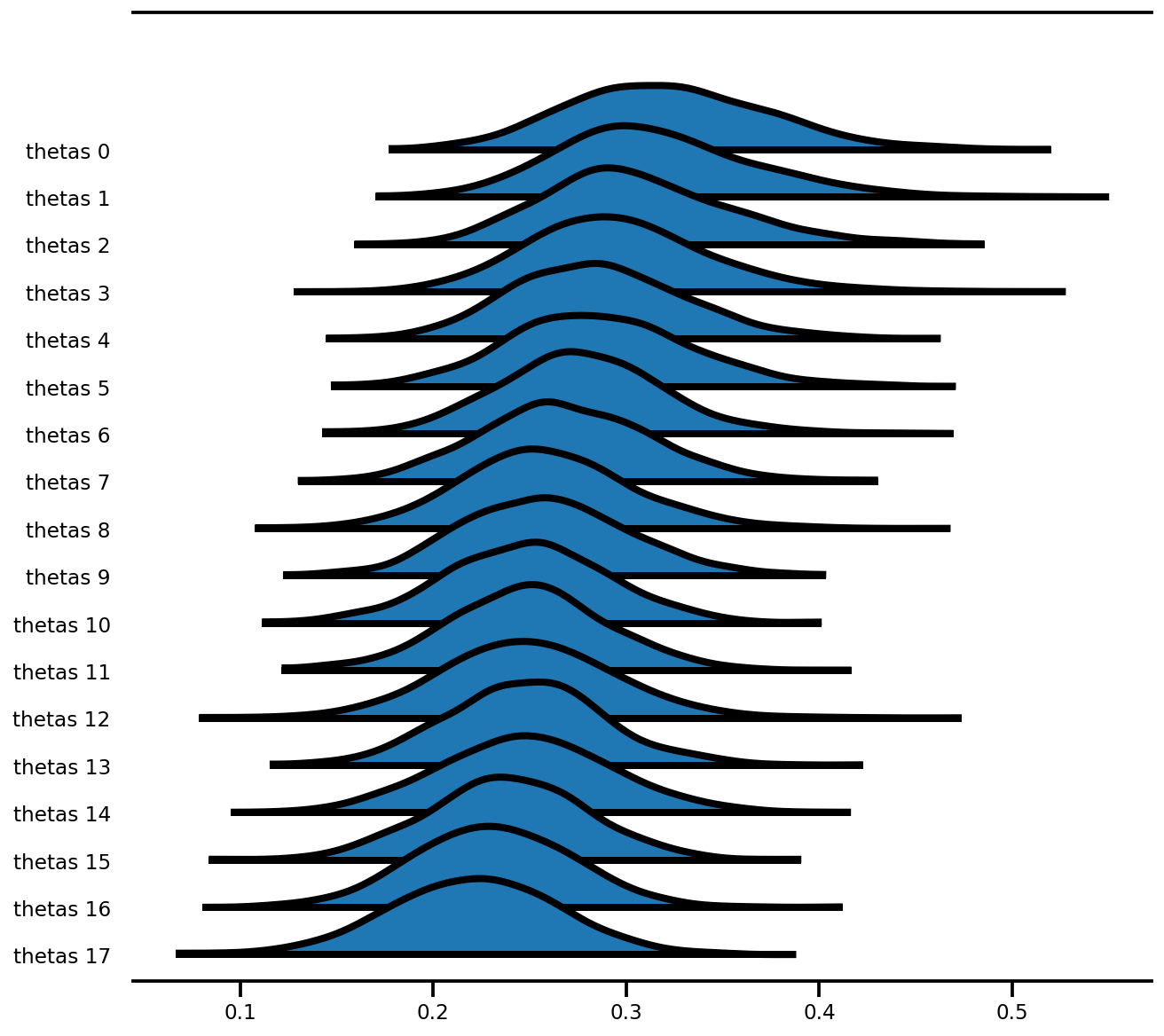
az.plot_forest(az_trace,
var_names=['thetas'],
kind='ridgeplot',
linewidth=4,
combined=True,
ridgeplot_overlap=1.5,
figsize=(9, 8));
Modelo de efectos mixtos (radón)
El último modelo en el doc PyMC3: Un manual sobre métodos bayesianos para Modelado de niveles múltiples
Algunos cambios en anteriores (menor escala, etc.)
Cargar datos sin procesar y limpiar
srrs2 = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/srrs2.dat')
srrs2.columns = srrs2.columns.map(str.strip)
srrs_mn = srrs2[srrs2.state=='MN'].copy()
srrs_mn['fips'] = srrs_mn.stfips*1000 + srrs_mn.cntyfips
cty = pd.read_csv('https://raw.githubusercontent.com/pymc-devs/pymc3/master/pymc3/examples/data/cty.dat')
cty_mn = cty[cty.st=='MN'].copy()
cty_mn[ 'fips'] = 1000*cty_mn.stfips + cty_mn.ctfips
srrs_mn = srrs_mn.merge(cty_mn[['fips', 'Uppm']], on='fips')
srrs_mn = srrs_mn.drop_duplicates(subset='idnum')
u = np.log(srrs_mn.Uppm)
n = len(srrs_mn)
srrs_mn.county = srrs_mn.county.map(str.strip)
mn_counties = srrs_mn.county.unique()
counties = len(mn_counties)
county_lookup = dict(zip(mn_counties, range(len(mn_counties))))
county = srrs_mn['county_code'] = srrs_mn.county.replace(county_lookup).values
radon = srrs_mn.activity
srrs_mn['log_radon'] = log_radon = np.log(radon + 0.1).values
floor_measure = srrs_mn.floor.values.astype('float')
# Create new variable for mean of floor across counties
xbar = srrs_mn.groupby('county')['floor'].mean().rename(county_lookup).values
Para modelos con transformación compleja, implementarlo en un estilo funcional facilitaría mucho la escritura y las pruebas. Además, hace que la función log_prob genere programáticamente que condicionó (mini-lote) de datos ingresados mucho más fácilmente:
def affine(u_val, x_county, county, floor, gamma, eps, b):
"""Linear equation of the coefficients and the covariates, with broadcasting."""
return (tf.transpose((gamma[..., 0]
+ gamma[..., 1]*u_val[:, None]
+ gamma[..., 2]*x_county[:, None]))
+ tf.gather(eps, county, axis=-1)
+ b*floor)
def gen_radon_model(u_val, x_county, county, floor,
mu0=tf.zeros([], dtype, name='mu0')):
"""Creates a joint distribution representing our generative process."""
return tfd.JointDistributionSequential([
# sigma_a
tfd.HalfCauchy(loc=mu0, scale=5.),
# eps
lambda sigma_a: tfd.Sample(
tfd.Normal(loc=mu0, scale=sigma_a), sample_shape=counties),
# gamma
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=3),
# b
tfd.Sample(tfd.Normal(loc=mu0, scale=100.), sample_shape=1),
# sigma_y
tfd.Sample(tfd.HalfCauchy(loc=mu0, scale=5.), sample_shape=1),
# likelihood
lambda sigma_y, b, gamma, eps: tfd.Independent(
tfd.Normal(
loc=affine(u_val, x_county, county, floor, gamma, eps, b),
scale=sigma_y
),
reinterpreted_batch_ndims=1
),
])
contextual_effect2 = gen_radon_model(
u.values, xbar[county], county, floor_measure)
@tf.function(autograph=False)
def unnormalized_posterior_log_prob(sigma_a, gamma, eps, b, sigma_y):
"""Computes `joint_log_prob` pinned at `log_radon`."""
return contextual_effect2.log_prob(
[sigma_a, gamma, eps, b, sigma_y, log_radon])
assert [4] == unnormalized_posterior_log_prob(
*contextual_effect2.sample(4)[:-1]).shape
samples = contextual_effect2.sample(4)
pprint([s.shape for s in samples])
[TensorShape([4]), TensorShape([4, 85]), TensorShape([4, 3]), TensorShape([4, 1]), TensorShape([4, 1]), TensorShape([4, 919])]
contextual_effect2.log_prob_parts(list(samples)[:-1] + [log_radon])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-3.95681828, -2.45693443, -2.53310078, -4.7717536 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-340.65975204, -217.11139018, -246.50498667, -369.79687704])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-20.49822449, -20.38052557, -18.63843525, -17.83096972])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-5.94765605, -5.91460848, -6.66169402, -5.53894593])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-2.10293999, -4.34186631, -2.10744955, -3.016717 ])>,
<tf.Tensor: shape=(4,), dtype=float64, numpy=
array([-29022322.1413861 , -114422.36893361, -8708500.81752865,
-35061.92497235])>]
Inferencia variacional
Una característica muy poderosa de JointDistribution* es que se puede generar fácilmente una aproximación de VI. Por ejemplo, para hacer ADVI de campo medio, simplemente inspecciona el gráfico y reemplaza toda la distribución no observada con una distribución Normal.
Meanfield ADVI
También puede utilizar la función de vivenciales en tensorflow_probability / python / experimental / VI para construir aproximación variacional, que son esencialmente la misma lógica utilizada a continuación (es decir, usando JointDistribution para construir aproximación), pero con la salida de aproximación en el espacio original en lugar de la espacio ilimitado.
from tensorflow_probability.python.mcmc.transformed_kernel import (
make_transform_fn, make_transformed_log_prob)
# Wrap logp so that all parameters are in the Real domain
# copied and edited from tensorflow_probability/python/mcmc/transformed_kernel.py
unconstraining_bijectors = [
tfb.Exp(),
tfb.Identity(),
tfb.Identity(),
tfb.Identity(),
tfb.Exp()
]
unnormalized_log_prob = lambda *x: contextual_effect2.log_prob(x + (log_radon,))
contextual_effect_posterior = make_transformed_log_prob(
unnormalized_log_prob,
unconstraining_bijectors,
direction='forward',
# TODO(b/72831017): Disable caching until gradient linkage
# generally works.
enable_bijector_caching=False)
# debug
if True:
# Check the two versions of log_prob - they should be different given the Jacobian
rv_samples = contextual_effect2.sample(4)
_inverse_transform = make_transform_fn(unconstraining_bijectors, 'inverse')
_forward_transform = make_transform_fn(unconstraining_bijectors, 'forward')
pprint([
unnormalized_log_prob(*rv_samples[:-1]),
contextual_effect_posterior(*_inverse_transform(rv_samples[:-1])),
unnormalized_log_prob(
*_forward_transform(
tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1])
),
contextual_effect_posterior(
*[tf.zeros_like(a, dtype=dtype) for a in rv_samples[:-1]]
),
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73354969e+04, -5.51622488e+04, -2.77754609e+08, -1.09065161e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1.73331358e+04, -5.51582029e+04, -2.77754602e+08, -1.09065134e+07])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-1992.10420767, -1992.10420767, -1992.10420767, -1992.10420767])>]
# Build meanfield ADVI for a jointdistribution
# Inspect the input jointdistribution and replace the list of distribution with
# a list of Normal distribution, each with the same shape.
def build_meanfield_advi(jd_list, observed_node=-1):
"""
The inputted jointdistribution needs to be a batch version
"""
# Sample to get a list of Tensors
list_of_values = jd_list.sample(1) # <== sample([]) might not work
# Remove the observed node
list_of_values.pop(observed_node)
# Iterate the list of Tensor to a build a list of Normal distribution (i.e.,
# the Variational posterior)
distlist = []
for i, value in enumerate(list_of_values):
dtype = value.dtype
rv_shape = value[0].shape
loc = tf.Variable(
tf.random.normal(rv_shape, dtype=dtype),
name='meanfield_%s_mu' % i,
dtype=dtype)
scale = tfp.util.TransformedVariable(
tf.fill(rv_shape, value=tf.constant(0.02, dtype)),
tfb.Softplus(),
name='meanfield_%s_scale' % i,
)
approx_node = tfd.Normal(loc=loc, scale=scale)
if loc.shape == ():
distlist.append(approx_node)
else:
distlist.append(
# TODO: make the reinterpreted_batch_ndims more flexible (for
# minibatch etc)
tfd.Independent(approx_node, reinterpreted_batch_ndims=1)
)
# pass list to JointDistribution to initiate the meanfield advi
meanfield_advi = tfd.JointDistributionSequential(distlist)
return meanfield_advi
advi = build_meanfield_advi(contextual_effect2, observed_node=-1)
# Check the logp and logq
advi_samples = advi.sample(4)
pprint([
advi.log_prob(advi_samples),
contextual_effect_posterior(*advi_samples)
])
[<tf.Tensor: shape=(4,), dtype=float64, numpy=array([231.26836839, 229.40755095, 227.10287879, 224.05914594])>, <tf.Tensor: shape=(4,), dtype=float64, numpy=array([-10615.93542431, -11743.21420129, -10376.26732337, -11338.00600103])>]
opt = tf.optimizers.Adam(learning_rate=.1)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior,
surrogate_posterior=advi,
optimizer=opt,
sample_size=10,
num_steps=300)
return loss_
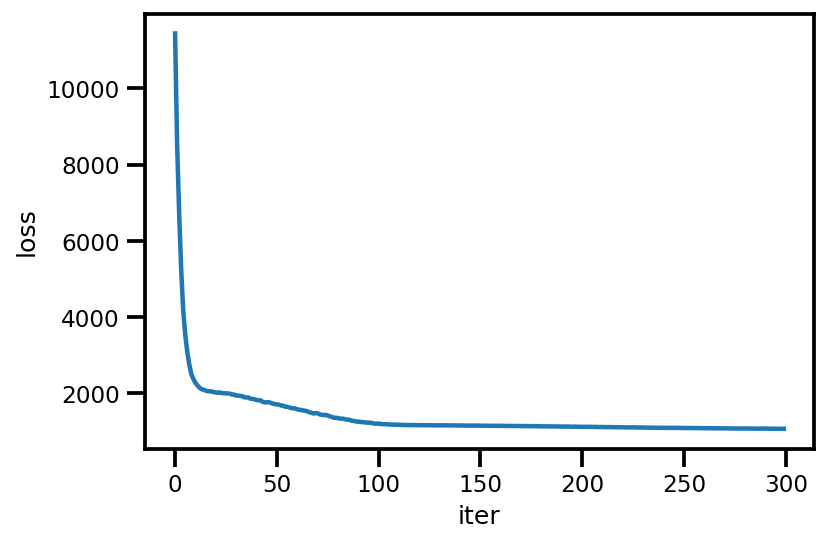
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param = advi.trainable_variables
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param[i*2].numpy(),
"sd": free_param[i*2+1].numpy()}
approx_param.keys()
dict_keys(['sigma_a', 'eps', 'gamma', 'b', 'sigma_y'])
approx_param['gamma']
{'mu': array([1.28145814, 0.70365287, 1.02689857]),
'sd': array([-3.6604972 , -2.68153218, -2.04176524])}
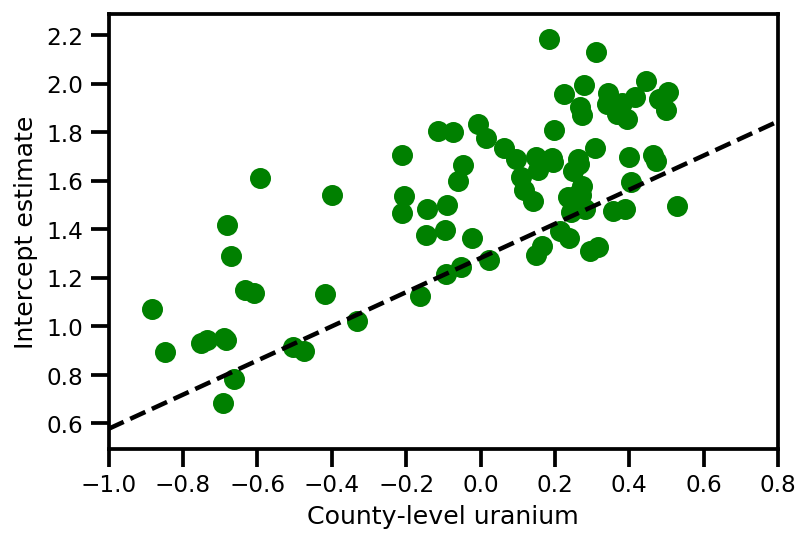
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
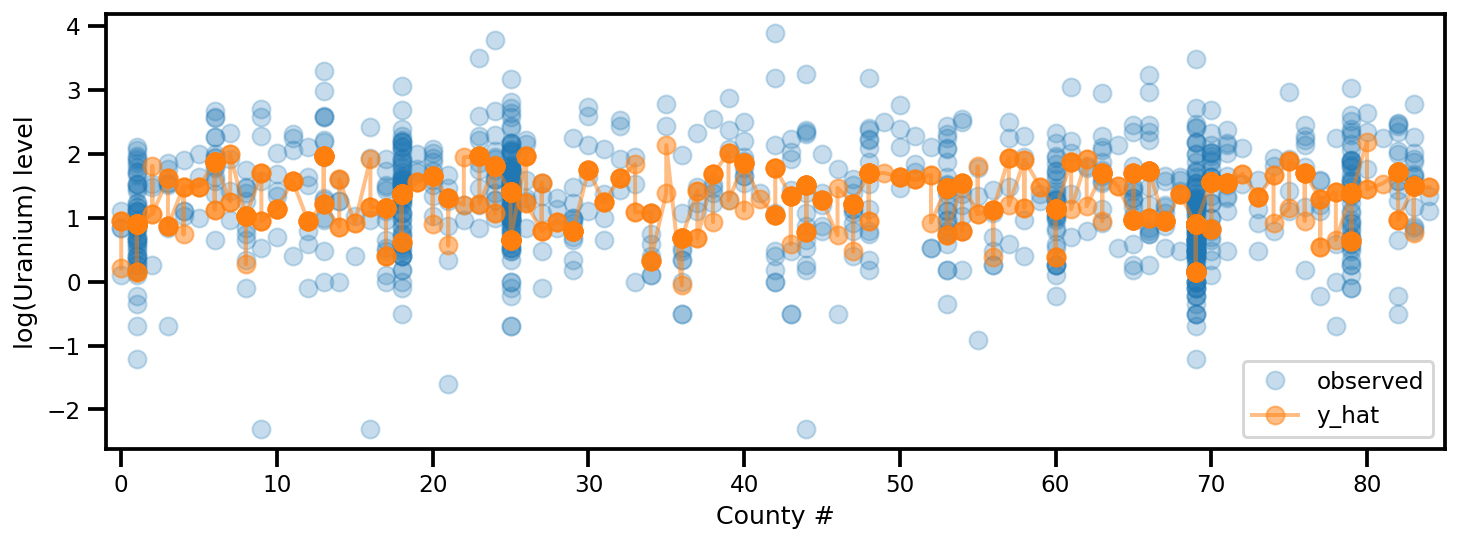
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
FullRank ADVI
Para ADVI de rango completo, queremos aproximar el posterior con un gaussiano multivariado.
USE_FULLRANK = True
*prior_tensors, _ = contextual_effect2.sample()
mapper = Mapper(prior_tensors,
[tfb.Identity() for _ in prior_tensors],
contextual_effect2.event_shape[:-1])
rv_shape = ps.shape(mapper.flatten_and_concat(mapper.list_of_tensors))
init_val = tf.random.normal(rv_shape, dtype=dtype)
loc = tf.Variable(init_val, name='loc', dtype=dtype)
if USE_FULLRANK:
# cov_param = tfp.util.TransformedVariable(
# 10. * tf.eye(rv_shape[0], dtype=dtype),
# tfb.FillScaleTriL(),
# name='cov_param'
# )
FillScaleTriL = tfb.FillScaleTriL(
diag_bijector=tfb.Chain([
tfb.Shift(tf.cast(.01, dtype)),
tfb.Softplus(),
tfb.Shift(tf.cast(np.log(np.expm1(1.)), dtype))]),
diag_shift=None)
cov_param = tfp.util.TransformedVariable(
.02 * tf.eye(rv_shape[0], dtype=dtype),
FillScaleTriL,
name='cov_param')
advi_approx = tfd.MultivariateNormalTriL(
loc=loc, scale_tril=cov_param)
else:
# An alternative way to build meanfield ADVI.
cov_param = tfp.util.TransformedVariable(
.02 * tf.ones(rv_shape, dtype=dtype),
tfb.Softplus(),
name='cov_param'
)
advi_approx = tfd.MultivariateNormalDiag(
loc=loc, scale_diag=cov_param)
contextual_effect_posterior2 = lambda x: contextual_effect_posterior(
*mapper.split_and_reshape(x)
)
# Check the logp and logq
advi_samples = advi_approx.sample(7)
pprint([
advi_approx.log_prob(advi_samples),
contextual_effect_posterior2(advi_samples)
])
[<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([238.81841799, 217.71022639, 234.57207103, 230.0643819 ,
243.73140943, 226.80149702, 232.85184209])>,
<tf.Tensor: shape=(7,), dtype=float64, numpy=
array([-3638.93663169, -3664.25879314, -3577.69371677, -3696.25705312,
-3689.12130489, -3777.53698383, -3659.4982734 ])>]
learning_rate = tf.optimizers.schedules.ExponentialDecay(
initial_learning_rate=1e-2,
decay_steps=10,
decay_rate=0.99,
staircase=True)
opt = tf.optimizers.Adam(learning_rate=learning_rate)
@tf.function(experimental_compile=True)
def run_approximation():
loss_ = tfp.vi.fit_surrogate_posterior(
contextual_effect_posterior2,
surrogate_posterior=advi_approx,
optimizer=opt,
sample_size=10,
num_steps=1000)
return loss_
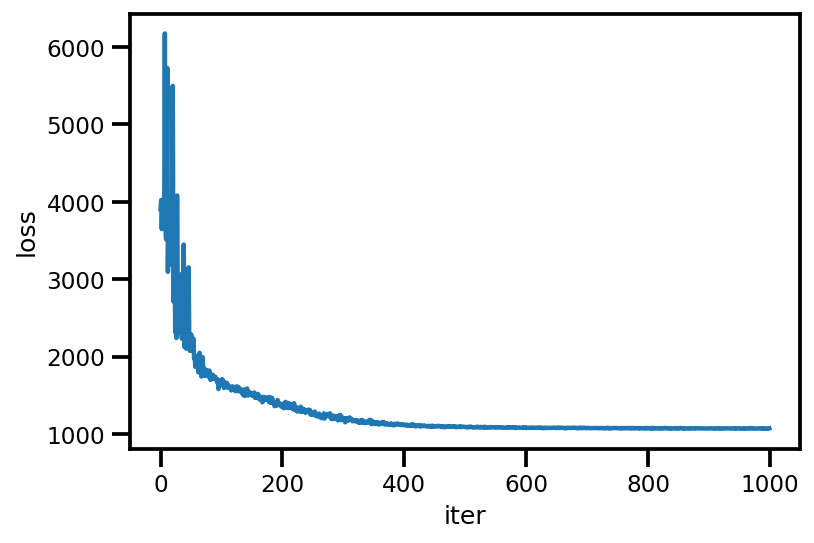
loss_ = run_approximation()
plt.plot(loss_);
plt.xlabel('iter');
plt.ylabel('loss');
# debug
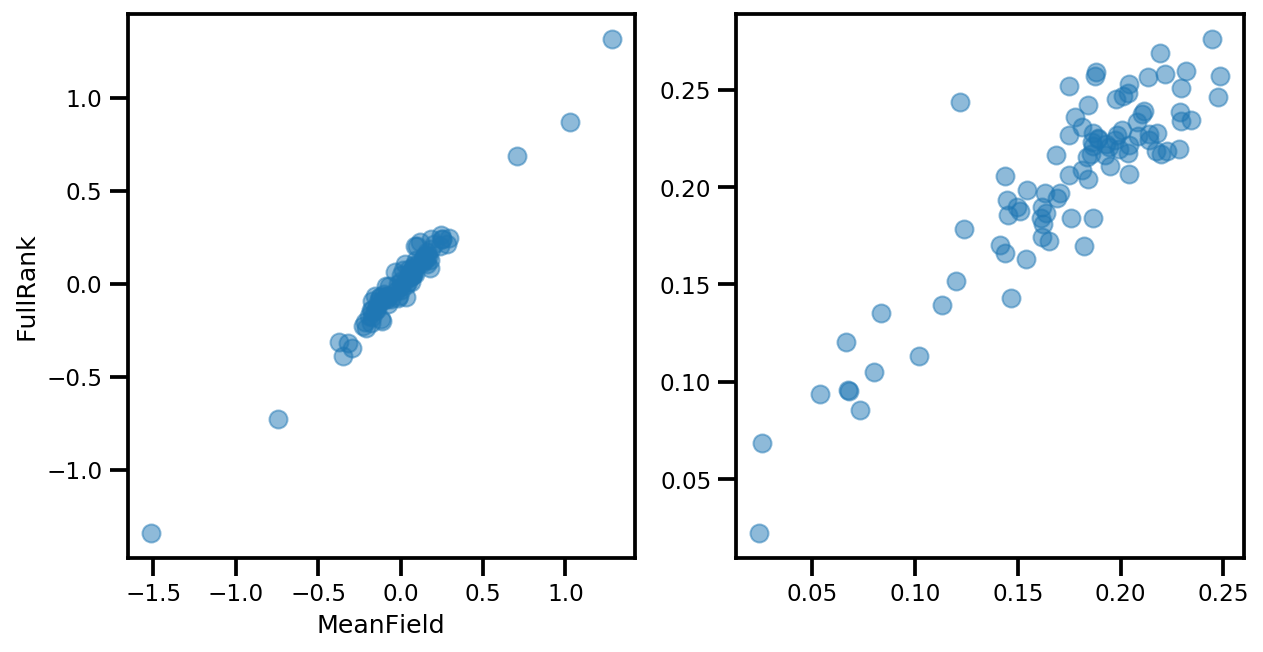
if True:
_, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(mapper.flatten_and_concat(advi.mean()), advi_approx.mean(), 'o', alpha=.5)
ax[1].plot(mapper.flatten_and_concat(advi.stddev()), advi_approx.stddev(), 'o', alpha=.5)
ax[0].set_xlabel('MeanField')
ax[0].set_ylabel('FullRank')
graph_info = contextual_effect2.resolve_graph()
approx_param = dict()
free_param_mean = mapper.split_and_reshape(advi_approx.mean())
free_param_std = mapper.split_and_reshape(advi_approx.stddev())
for i, (rvname, param) in enumerate(graph_info[:-1]):
approx_param[rvname] = {"mu": free_param_mean[i].numpy(),
"cov_info": free_param_std[i].numpy()}
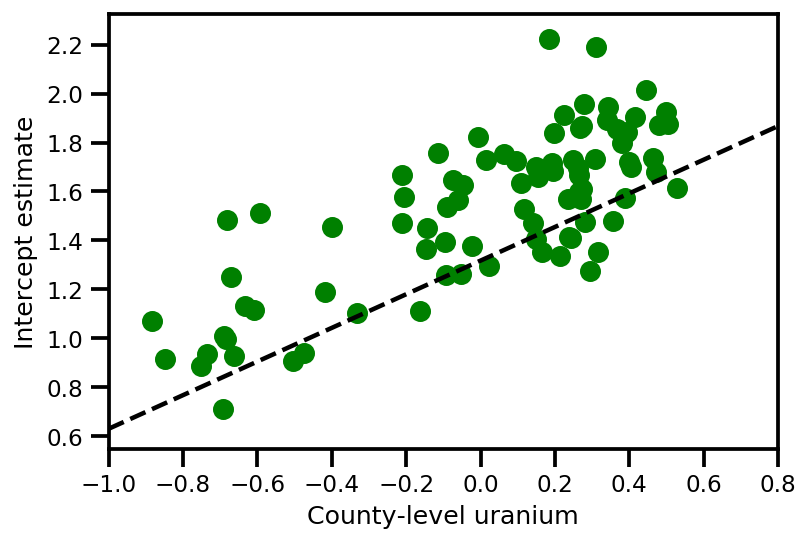
a_means = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county])
_, index = np.unique(county, return_index=True)
plt.scatter(u.values[index], a_means[index], color='g')
xvals = np.linspace(-1, 0.8)
plt.plot(xvals,
approx_param['gamma']['mu'][0]+approx_param['gamma']['mu'][1]*xvals,
'k--')
plt.xlim(-1, 0.8)
plt.xlabel('County-level uranium');
plt.ylabel('Intercept estimate');
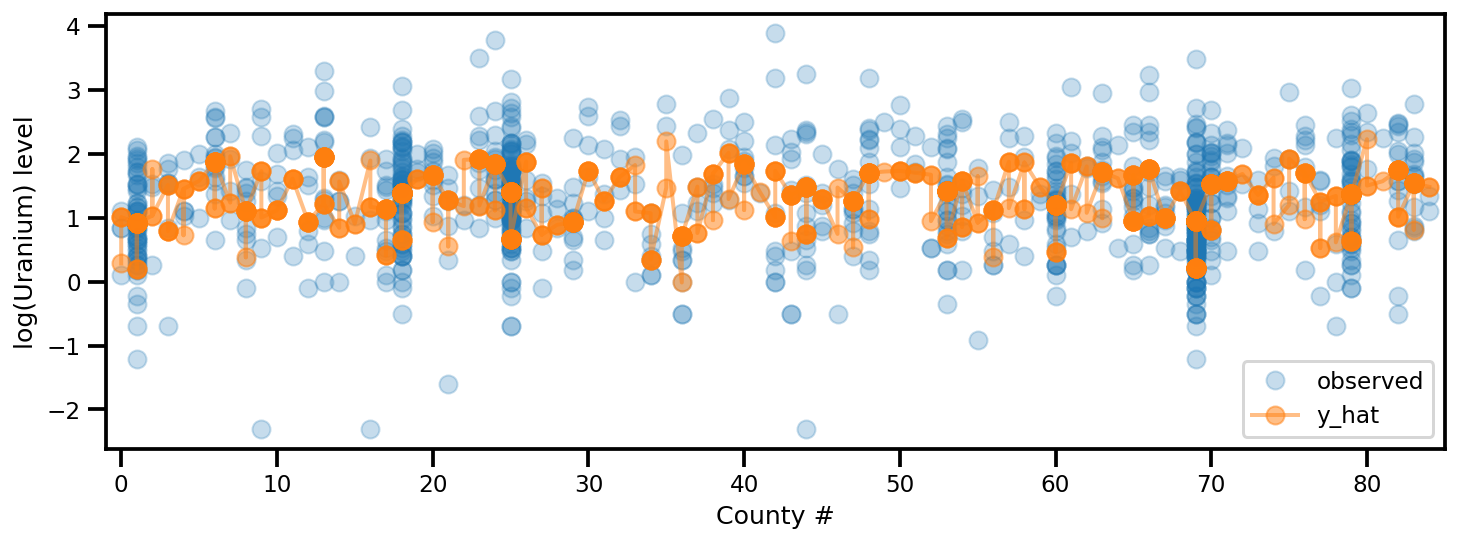
y_est = (approx_param['gamma']['mu'][0]
+ approx_param['gamma']['mu'][1]*u.values
+ approx_param['gamma']['mu'][2]*xbar[county]
+ approx_param['eps']['mu'][county]
+ approx_param['b']['mu']*floor_measure)
_, ax = plt.subplots(1, 1, figsize=(12, 4))
ax.plot(county, log_radon, 'o', alpha=.25, label='observed')
ax.plot(county, y_est, '-o', lw=2, alpha=.5, label='y_hat')
ax.set_xlim(-1, county.max()+1)
plt.legend(loc='lower right')
ax.set_xlabel('County #')
ax.set_ylabel('log(Uranium) level');
Modelo de mezcla Beta-Bernoulli
Un modelo mixto en el que varios revisores etiquetan algunos artículos con etiquetas latentes desconocidas (verdaderas).
dtype = tf.float32
n = 50000 # number of examples reviewed
p_bad_ = 0.1 # fraction of bad events
m = 5 # number of reviewers for each example
rcl_ = .35 + np.random.rand(m)/10
prc_ = .65 + np.random.rand(m)/10
# PARAMETER TRANSFORMATION
tpr = rcl_
fpr = p_bad_*tpr*(1./prc_-1.)/(1.-p_bad_)
tnr = 1 - fpr
# broadcast to m reviewer.
batch_prob = np.asarray([tpr, fpr]).T
mixture = tfd.Mixture(
tfd.Categorical(
probs=[p_bad_, 1-p_bad_]),
[
tfd.Independent(tfd.Bernoulli(probs=tpr), 1),
tfd.Independent(tfd.Bernoulli(probs=fpr), 1),
])
# Generate reviewer response
X_tf = mixture.sample([n])
# run once to always use the same array as input
# so we can compare the estimation from different
# inference method.
X_np = X_tf.numpy()
# batched Mixture model
mdl_mixture = tfd.JointDistributionSequential([
tfd.Sample(tfd.Beta(5., 2.), m),
tfd.Sample(tfd.Beta(2., 2.), m),
tfd.Sample(tfd.Beta(1., 10), 1),
lambda p_bad, rcl, prc: tfd.Sample(
tfd.Mixture(
tfd.Categorical(
probs=tf.concat([p_bad, 1.-p_bad], -1)),
[
tfd.Independent(tfd.Bernoulli(
probs=rcl), 1),
tfd.Independent(tfd.Bernoulli(
probs=p_bad*rcl*(1./prc-1.)/(1.-p_bad)), 1)
]
), (n, )),
])
mdl_mixture.resolve_graph()
(('prc', ()), ('rcl', ()), ('p_bad', ()), ('x', ('p_bad', 'rcl', 'prc')))
prc, rcl, p_bad, x = mdl_mixture.sample(4)
x.shape
TensorShape([4, 50000, 5])
mdl_mixture.log_prob_parts([prc, rcl, p_bad, X_np[np.newaxis, ...]])
[<tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.4828572, 2.957961 , 2.9355168, 2.6116824], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.14646745, 1.3308513 , 1.1205603 , 0.5441705 ], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([1.3733709, 1.8020535, 2.1865845, 1.5701319], dtype=float32)>, <tf.Tensor: shape=(4,), dtype=float32, numpy=array([-54326.664, -52683.93 , -64407.67 , -55007.895], dtype=float32)>]
Inferencia (NUTS)
nchain = 10
prc, rcl, p_bad, _ = mdl_mixture.sample(nchain)
initial_chain_state = [prc, rcl, p_bad]
# Since MCMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
unconstraining_bijectors = [
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
tfb.Sigmoid(), # Maps R to [0, 1].
]
step_size = [tf.cast(i, dtype=dtype) for i in [1e-3, 1e-3, 1e-3]]
X_expanded = X_np[np.newaxis, ...]
target_log_prob_fn = lambda *x: mdl_mixture.log_prob(x + (X_expanded, ))
samples, sampler_stat = run_chain(
initial_chain_state, step_size, target_log_prob_fn,
unconstraining_bijectors, burnin=100)
# using the pymc3 naming convention
sample_stats_name = ['lp', 'tree_size', 'diverging', 'energy', 'mean_tree_accept']
sample_stats = {k:v.numpy().T for k, v in zip(sample_stats_name, sampler_stat)}
sample_stats['tree_size'] = np.diff(sample_stats['tree_size'], axis=1)
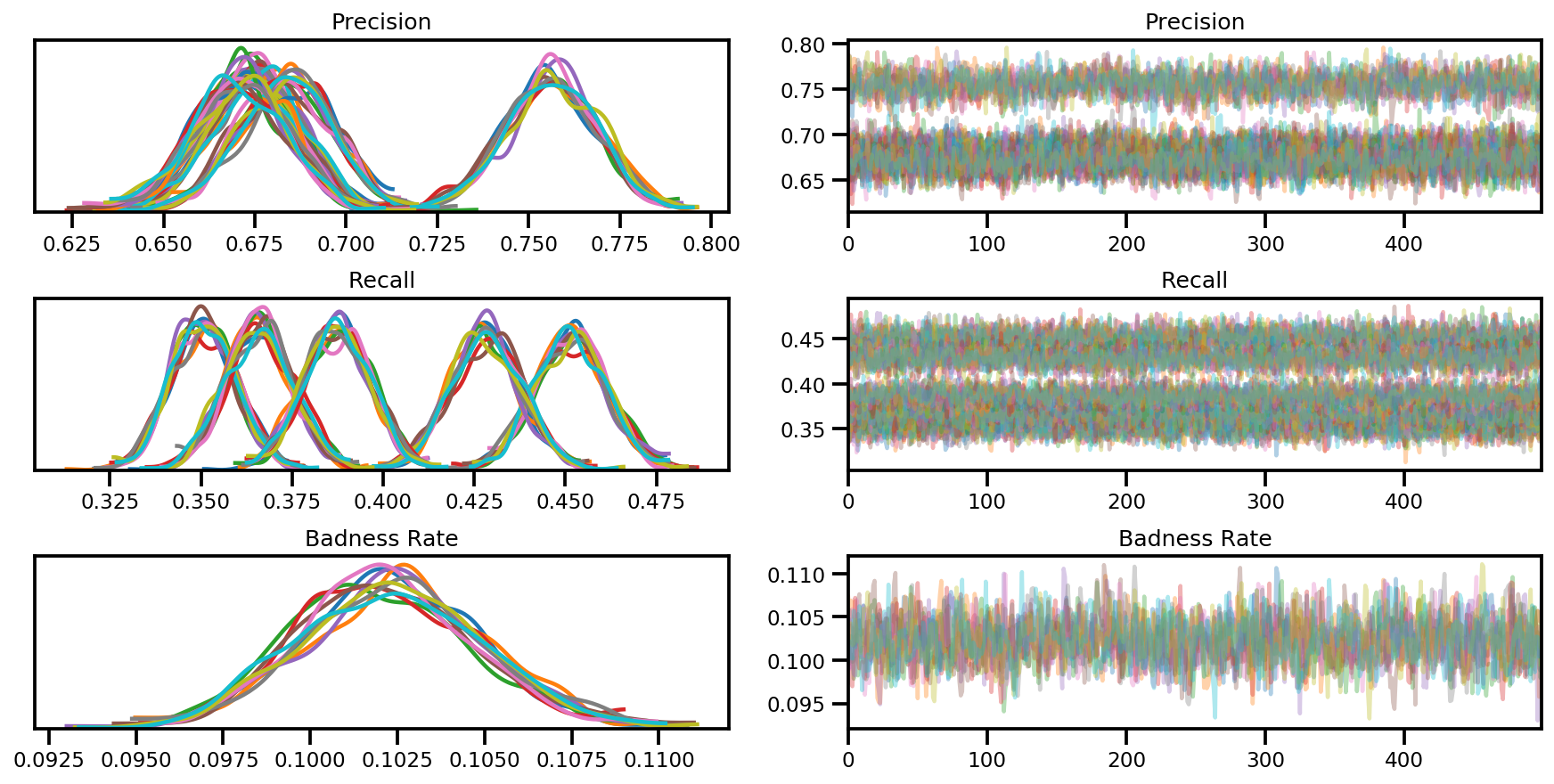
var_name = ['Precision', 'Recall', 'Badness Rate']
posterior = {k:np.swapaxes(v.numpy(), 1, 0)
for k, v in zip(var_name, samples)}
az_trace = az.from_dict(posterior=posterior, sample_stats=sample_stats)
axes = az.plot_trace(az_trace, compact=True);