โมเดลเอฟเฟกต์ผสมเชิงเส้น

ดูบน TensorFlow.org

ทำงานใน Google Colab

ดูแหล่งที่มาบน GitHub

ดาวน์โหลดโน๊ตบุ๊ค

แบบจำลองเอฟเฟกต์ผสมเชิงเส้นเป็นแนวทางง่ายๆ สำหรับการสร้างแบบจำลองความสัมพันธ์เชิงเส้นที่มีโครงสร้าง (Harville, 1997; Laird and Ware, 1982) จุดข้อมูลแต่ละจุดประกอบด้วยอินพุตประเภทต่างๆ—แบ่งออกเป็นกลุ่ม—และเอาต์พุตที่มีมูลค่าจริง เชิงเส้นแบบจำลองผลกระทบผสมเป็นรูปแบบลำดับชั้น: หุ้นมันมีความแข็งแรงทางสถิติในทุกกลุ่มเพื่อที่จะปรับปรุงการหาข้อสรุปเกี่ยวกับจุดข้อมูลใด ๆ ของแต่ละบุคคล

ในบทช่วยสอนนี้ เราสาธิตโมเดลเอฟเฟกต์เชิงเส้นแบบผสมพร้อมตัวอย่างในโลกแห่งความเป็นจริงในความน่าจะเป็นของ TensorFlow เราจะใช้ JointDistributionCoroutine และ Markov Chain Monte Carlo ( tfp.mcmc ) โมดูล

การพึ่งพาและข้อกำหนดเบื้องต้น

นำเข้าและตั้งค่า

import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp

tfd = tfp.distributions
tfb = tfp.bijectors

dtype = tf.float64

%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')

ทำสิ่งที่รวดเร็ว!

ก่อนที่เราจะเจาะลึก มาทำให้มั่นใจว่าเรากำลังใช้ GPU สำหรับการสาธิตนี้

ในการดำเนินการนี้ ให้เลือก "รันไทม์" -> "เปลี่ยนประเภทรันไทม์" -> "ตัวเร่งฮาร์ดแวร์" -> "GPU"

ตัวอย่างต่อไปนี้จะตรวจสอบว่าเรามีสิทธิ์เข้าถึง GPU

if tf.test.gpu_device_name() != '/device:GPU:0':
  print('WARNING: GPU device not found.')
else:
  print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))

SUCCESS: Found GPU: /device:GPU:0

ข้อมูล

เราใช้ InstEval ชุดข้อมูลจากความนิยม lme4 แพคเกจใน R (เบตส์ et al., 2015) เป็นชุดข้อมูลของหลักสูตรและการให้คะแนนการประเมิน แน่นอนว่าแต่ละคนรวมถึงข้อมูลเมตาเช่น students , instructors และ departments และตัวแปรการตอบสนองที่น่าสนใจคือคะแนนการประเมินผล

def load_insteval():
  """Loads the InstEval data set.

  It contains 73,421 university lecture evaluations by students at ETH
  Zurich with a total of 2,972 students, 2,160 professors and
  lecturers, and several student, lecture, and lecturer attributes.
  Implementation is built from the `observations` Python package.

  Returns:
    Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
    dictionary `metadata` of column headers (feature names).
  """
  url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
         'lme4/InstEval.csv')
  with requests.Session() as s:
    download = s.get(url)
    f = download.content.decode().splitlines()

  iterator = csv.reader(f)
  columns = next(iterator)[1:]
  x_train = np.array([row[1:] for row in iterator], dtype=np.int)
  metadata = {'columns': columns}
  return x_train, metadata

เราโหลดและประมวลผลชุดข้อมูลล่วงหน้า เราเก็บข้อมูลไว้ 20% เพื่อให้เราสามารถประเมินแบบจำลองที่ติดตั้งของเราบนจุดข้อมูลที่มองไม่เห็น ด้านล่างเราจะเห็นภาพสองสามแถวแรก

data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
                            'd': 'instructors',
                            'dept': 'departments',
                            'y': 'ratings'})
data['students'] -= 1  # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes

train = data.sample(frac=0.8)
test = data.drop(train.index)

train.head()

เราตั้งค่าชุดข้อมูลในแง่ของ features ในพจนานุกรมของปัจจัยการผลิตและ labels เอาท์พุทที่สอดคล้องกับการจัดอันดับ แต่ละคุณลักษณะถูกเข้ารหัสเป็นจำนวนเต็ม และแต่ละป้ายกำกับ (การประเมินการประเมิน) ถูกเข้ารหัสเป็นตัวเลขทศนิยม

get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
    k: get_value(train, key=k, dtype=np.int32)
    for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)

features_test = {k: get_value(test, key=k, dtype=np.int32)
                 for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)

num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]

print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)

Number of students: 2972
Number of instructors: 1128
Number of departments: 14
Number of observations: 58737

แบบอย่าง

แบบจำลองเชิงเส้นทั่วไปถือว่ามีความเป็นอิสระ โดยที่จุดข้อมูลคู่ใดๆ มีความสัมพันธ์เชิงเส้นคงที่ ใน InstEval ชุดข้อมูลการสังเกตเกิดขึ้นในกลุ่มแต่ละที่อาจมีเนินเขาและดักที่แตกต่างกัน แบบจำลองเอฟเฟกต์เชิงเส้นแบบผสม หรือที่เรียกว่าแบบจำลองเชิงเส้นแบบลำดับชั้นหรือแบบจำลองเชิงเส้นหลายระดับ จับภาพปรากฏการณ์นี้ (Gelman & Hill, 2006)

ตัวอย่างของปรากฏการณ์นี้ได้แก่:

• นักเรียน การสังเกตจากนักเรียนไม่ได้เป็นอิสระ: นักเรียนบางคนอาจให้คะแนนการบรรยายต่ำ (หรือสูง) อย่างเป็นระบบ
• อาจารย์ผู้สอน การสังเกตจากผู้สอนไม่ได้เป็นอิสระ: เราคาดหวังให้ครูที่ดีมักจะได้รับคะแนนที่ดีและครูที่ไม่ดีมักจะมีการให้คะแนนที่ไม่ดี
• หน่วยงาน ข้อสังเกตจากแผนกหนึ่งไม่เป็นอิสระ: โดยทั่วไปแล้วบางแผนกอาจมีเนื้อหาที่แห้งหรือมีการจัดระดับที่เข้มงวดกว่า ดังนั้นจึงได้รับการจัดอันดับที่ต่ำกว่าแผนกอื่นๆ

การจับภาพนี้เรียกว่าสำหรับชุดข้อมูลของ \(N\times D\) มี \(\mathbf{X}\) และ \(N\) ป้าย \(\mathbf{y}\), posits ถดถอยเชิงเส้นรูปแบบ

\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]

ที่มีความลาดชันเวกเตอร์ \(\beta\in\mathbb{R}^D\)ตัด \(\alpha\in\mathbb{R}\)และสุ่มเสียง \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)เราบอกว่า \(\beta\) และ \(\alpha\) คือ "ผลกระทบคงที่" พวกเขามีผลกระทบที่จัดขึ้นอย่างต่อเนื่องทั่วประชากรจุดข้อมูล \((x, y)\)สูตรเทียบเท่าของสมการเป็นโอกาสเป็น \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\)โอกาสนี้จะขยายช่วงการอนุมานเพื่อหาจุดของการประมาณการ \(\beta\) และ \(\alpha\) ที่เหมาะสมกับข้อมูล

แบบจำลองเอฟเฟกต์ผสมเชิงเส้นขยายการถดถอยเชิงเส้นเป็น

\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]

ที่ยังคงมีความลาดชันเวกเตอร์ \(\beta\in\mathbb{R}^P\)ตัด \(\alpha\in\mathbb{R}\)และสุ่มเสียง \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)นอกจากนี้ยังมีเป็นระยะ \(\mathbf{Z}\eta\)ที่ \(\mathbf{Z}\) เป็นเมทริกซ์คุณสมบัติและ \(\eta\in\mathbb{R}^Q\) เป็นเวกเตอร์ของลาดสุ่ม \(\eta\) มีการกระจายตามปกติที่มีความแปรปรวนพารามิเตอร์องค์ประกอบ \(\sigma^2\)\(\mathbf{Z}\) จะเกิดขึ้นโดยแบ่งเดิม \(N\times D\) มีเมทริกซ์ในแง่ของใหม่ \(N\times P\) เมทริกซ์ \(\mathbf{X}\) และ \(N\times Q\) เมทริกซ์ \(\mathbf{Z}\)ที่ \(P + Q=D\): พาร์ทิชันนี้ช่วยให้เราสามารถสร้างแบบจำลองลักษณะการแยกใช้ ผลกระทบคง \(\beta\) และตัวแปรแฝง \(\eta\) ตามลำดับ

เราบอกว่าตัวแปรแฝง \(\eta\) คือ "ผลกระทบสุ่ม" พวกเขามีผลกระทบที่แตกต่างกันในประชากร (แม้ว่าพวกเขาอาจจะมีอย่างต่อเนื่องทั่วประชากร) โดยเฉพาะอย่างยิ่งเพราะผลกระทบที่สุ่ม \(\eta\) มีค่าเฉลี่ย 0 เฉลี่ยฉลากข้อมูลที่ถูกจับโดย \(\mathbf{X}\beta + \alpha\)ผลกระทบสุ่มองค์ประกอบ \(\mathbf{Z}\eta\) จับการเปลี่ยนแปลงของข้อมูล: "สอน # 54 จัดอยู่ในอันดับ 1.4 คะแนนสูงกว่าค่าเฉลี่ย" ยกตัวอย่างเช่น

ในบทช่วยสอนนี้ เราใส่เอฟเฟกต์ต่อไปนี้:

• ผลกระทบคงที่: service service เป็นตัวแปรร่วมไบนารีที่สอดคล้องกันว่าการเรียนการสอนเป็นแผนกหลักของอาจารย์ผู้สอน ไม่ว่าข้อมูลที่เราเก็บรวบรวมเพิ่มเติมก็สามารถใช้เวลาในการค่า \(0\) และ \(1\)
• ผลกระทบสุ่ม: students , instructors และ departments จากการสังเกตเพิ่มเติมจากจำนวนประชากรของการให้คะแนนการประเมินหลักสูตร เราอาจกำลังมองหานักเรียน อาจารย์ หรือแผนกใหม่

ในไวยากรณ์ของแพ็คเกจ lme4 ของ R (Bates et al., 2015) โมเดลสามารถสรุปได้ดังนี้

ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1

ที่ x หมายถึงผลคงที่ (1|x) หมายถึงผลการสุ่มสำหรับ x และ 1 หมายถึงคำที่ตัด

เราใช้โมเดลนี้ด้านล่างเป็น JointDistribution จะมีการสนับสนุนที่ดีขึ้นสำหรับการติดตามพารามิเตอร์ (เช่นเราต้องการที่จะติดตามทุก tf.Variable ใน model.trainable_variables ) เราใช้เทมเพลตแบบเป็น tf.Module

class LinearMixedEffectModel(tf.Module):
  def __init__(self):
    # Set up fixed effects and other parameters.
    # These are free parameters to be optimized in E-steps
    self._intercept = tf.Variable(0., name="intercept")            # alpha in eq
    self._effect_service = tf.Variable(0., name="effect_service")  #  beta in eq
    self._stddev_students = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_students")            # sigma in eq
    self._stddev_instructors = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_instructors")         # sigma in eq
    self._stddev_departments = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_departments")         # sigma in eq

  def __call__(self, features):
    model = tfd.JointDistributionSequential([
      # Set up random effects.
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_students),
          scale_identity_multiplier=self._stddev_students),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_instructors),
          scale_identity_multiplier=self._stddev_instructors),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_departments),
          scale_identity_multiplier=self._stddev_departments),
      # This is the likelihood for the observed.
      lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
          tfd.Normal(
              loc=(self._effect_service * features["service"] +
                  tf.gather(effect_students, features["students"], axis=-1) +
                  tf.gather(effect_instructors, features["instructors"], axis=-1) +
                  tf.gather(effect_departments, features["departments"], axis=-1) +
                  self._intercept),
              scale=1.),
              reinterpreted_batch_ndims=1)
    ])

    # To enable tracking of the trainable variables via the created distribution,
    # we attach a reference to `self`. Since all TFP objects sub-class
    # `tf.Module`, this means that the following is possible:
    # LinearMixedEffectModel()(features_train).trainable_variables
    # ==> tuple of all tf.Variables created by LinearMixedEffectModel.
    model._to_track = self
    return model

lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)

lmm_train.trainable_variables

(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)

ในฐานะโปรแกรมกราฟิกความน่าจะเป็น เรายังสามารถเห็นภาพโครงสร้างของแบบจำลองในแง่ของกราฟการคำนวณ กราฟนี้เข้ารหัสการไหลของข้อมูลในตัวแปรสุ่มในโปรแกรม ทำให้ความสัมพันธ์ชัดเจนในแง่ของแบบจำลองกราฟิก (Jordan, 2003)

ในฐานะที่เป็นเครื่องมือทางสถิติเราอาจจะดูกราฟเพื่อให้ดูดีขึ้นตัวอย่างเช่นที่ intercept และ effect_service เป็นเงื่อนไขที่กำหนดขึ้นอยู่กับ ratings ; สิ่งนี้อาจมองเห็นได้ยากกว่าจากซอร์สโค้ดหากโปรแกรมเขียนด้วยคลาส การอ้างอิงโยงข้ามโมดูล และ/หรือรูทีนย่อย เป็นเครื่องมือในการคำนวณเรายังอาจสังเกตเห็นตัวแปรแฝงไหลลงสู่ ratings ตัวแปรผ่าน tf.gather Ops นี้อาจจะเป็นคอขวดในการเร่งฮาร์ดแวร์บางอย่างถ้าทำดัชนี Tensor คือราคาแพง การแสดงภาพกราฟทำให้สิ่งนี้ชัดเจน

lmm_train.resolve_graph()

(('effect_students', ()),
 ('effect_instructors', ()),
 ('effect_departments', ()),
 ('x', ('effect_departments', 'effect_instructors', 'effect_students')))

การประมาณค่าพารามิเตอร์

ข้อมูลที่กำหนดเป้าหมายของการอนุมานที่จะเหมาะสมกับรูปแบบของผลกระทบที่คงที่ลาด \(\beta\)ตัด \(\alpha\)และความแปรปรวนพารามิเตอร์องค์ประกอบ \(\sigma^2\)หลักการความเป็นไปได้สูงสุดทำให้งานนี้เป็นทางการเป็น

\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]

ในบทช่วยสอนนี้ เราใช้อัลกอริธึม Monte Carlo EM เพื่อเพิ่มความหนาแน่นส่วนขอบให้สูงสุด (Dempster et al., 1977; Wei and Tanner, 1990)¹ เราดำเนินการ Markov chain Monte Carlo เพื่อคำนวณความคาดหวังของความเป็นไปได้ตามเงื่อนไขที่สัมพันธ์กับ เอฟเฟกต์แบบสุ่ม ("E-step") และเราทำการไล่ระดับลงเพื่อเพิ่มความคาดหวังสูงสุดตามพารามิเตอร์ ("M-step"):

• สำหรับ E-step เราตั้งค่า Hamiltonian Monte Carlo (HMC) ต้องใช้สถานะปัจจุบัน—นักเรียน ผู้สอน และผลกระทบของแผนก—และคืนสถานะใหม่ เรากำหนดสถานะใหม่ให้กับตัวแปร TensorFlow ซึ่งจะแสดงถึงสถานะของสายโซ่ HMC

• สำหรับขั้นตอน M เราใช้ตัวอย่างหลังจาก HMC เพื่อคำนวณค่าประมาณที่เป็นกลางของความเป็นไปได้ที่จะเพิ่มเป็นค่าคงที่ จากนั้นเราใช้การไล่ระดับสีตามพารามิเตอร์ที่น่าสนใจ สิ่งนี้สร้างขั้นตอนการสืบเชื้อสายสุ่มที่เป็นกลางบนความน่าจะเป็นส่วนเพิ่ม เราปรับใช้กับเครื่องมือเพิ่มประสิทธิภาพ Adam TensorFlow และลดค่าลบของส่วนเพิ่ม

target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]

# For debugging
target_log_prob_fn(*current_state)

<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>

# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=target_log_prob_fn,
    step_size=0.015,
    num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)

@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
  next_state, next_kernel_results = hmc.one_step(
      current_state=current_state,
      previous_kernel_results=kernel_results)
  return next_state, next_kernel_results

optimizer = tf.optimizers.Adam(learning_rate=.01)

# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
  with tf.GradientTape() as tape:
    loss = -target_log_prob_fn(*current_state)
  grads = tape.gradient(loss, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss

เราทำขั้นตอนการวอร์มอัพ ซึ่งดำเนินการหนึ่งห่วงโซ่ MCMC สำหรับการทำซ้ำหลาย ๆ ครั้ง เพื่อให้การฝึกอบรมสามารถเริ่มต้นได้ภายในมวลความน่าจะเป็นของส่วนหลัง จากนั้นเราเรียกใช้วงจรการฝึกอบรม ร่วมกันดำเนินการขั้นตอน E และ M และบันทึกค่าระหว่างการฝึกอบรม

num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])

# Run warm-up stage.
for t in range(num_warmup_iters):
  current_state, kernel_results = one_e_step(current_state, kernel_results)
  num_accepted += kernel_results.is_accepted.numpy()
  if t % 500 == 0 or t == num_warmup_iters - 1:
    print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
        t, num_accepted / (t + 1)))

num_accepted = 0  # reset acceptance rate counter

# Run training.
for t in range(num_iters):
  # run 5 MCMC iterations before every joint EM update
  for _ in range(5):
    current_state, kernel_results = one_e_step(current_state, kernel_results)
  loss = one_m_step(current_state)
  effect_students_samples[t, :] = current_state[0].numpy()
  effect_instructors_samples[t, :] = current_state[1].numpy()
  effect_departments_samples[t, :] = current_state[2].numpy()
  num_accepted += kernel_results.is_accepted.numpy()
  loss_history[t] = loss.numpy()
  if t % 500 == 0 or t == num_iters - 1:
    print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
        t, num_accepted / (t + 1), loss_history[t]))

Warm-Up Iteration:   0 Acceptance Rate: 1.000
Warm-Up Iteration: 500 Acceptance Rate: 0.754
Warm-Up Iteration: 999 Acceptance Rate: 0.707
Iteration:    0 Acceptance Rate: 1.000 Loss: 98220.266
Iteration:  500 Acceptance Rate: 0.703 Loss: 96003.969
Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609
Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891

นอกจากนี้คุณยังสามารถเขียนวอร์มสำหรับวงเป็น tf.while_loop และขั้นตอนการฝึกอบรมเป็น tf.scan หรือ tf.while_loop สำหรับอนุมานได้เร็วยิ่งขึ้น ตัวอย่างเช่น:

@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
  _, next_state, next_kernel_results = tf.while_loop(
      cond=lambda i, state, pkr: i < k,
      body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
      loop_vars=(tf.constant(0), current_state, kernel_results)
  )
  return next_state, next_kernel_results

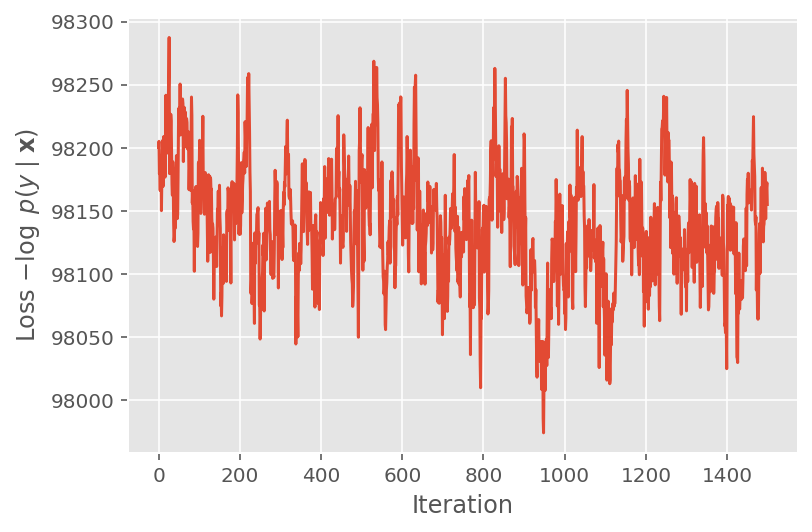
ด้านบน เราไม่ได้เรียกใช้อัลกอริทึมจนกว่าจะตรวจพบเกณฑ์การบรรจบกัน เพื่อตรวจสอบว่าการฝึกอบรมเหมาะสมหรือไม่ เราตรวจสอบว่าฟังก์ชันการสูญเสียมีแนวโน้มที่จะมาบรรจบกันมากกว่าการฝึกซ้ำ

plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()

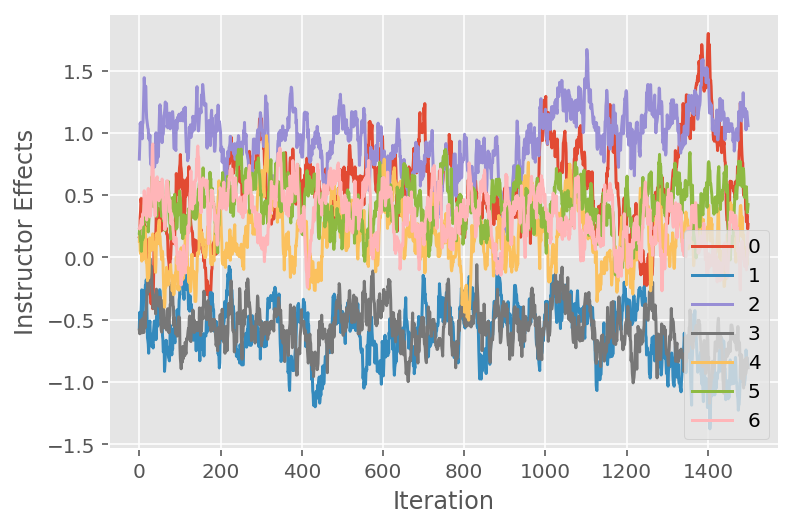
เรายังใช้พล็อตการติดตาม ซึ่งแสดงเส้นทางของอัลกอริธึมของ Markov chain Monte Carlo ในมิติที่ซ่อนเร้นเฉพาะ ด้านล่างเราจะเห็นว่าผลกระทบของผู้สอนแต่ละคนมีความหมายเปลี่ยนจากสถานะเริ่มต้นและสำรวจพื้นที่ของรัฐอย่างมีความหมาย พล็อตการติดตามยังบ่งชี้ว่าผลกระทบแตกต่างกันไปตามผู้สอน แต่มีพฤติกรรมการผสมที่คล้ายคลึงกัน

for i in range(7):
  plt.plot(effect_instructors_samples[:, i])

plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()

คำติชม

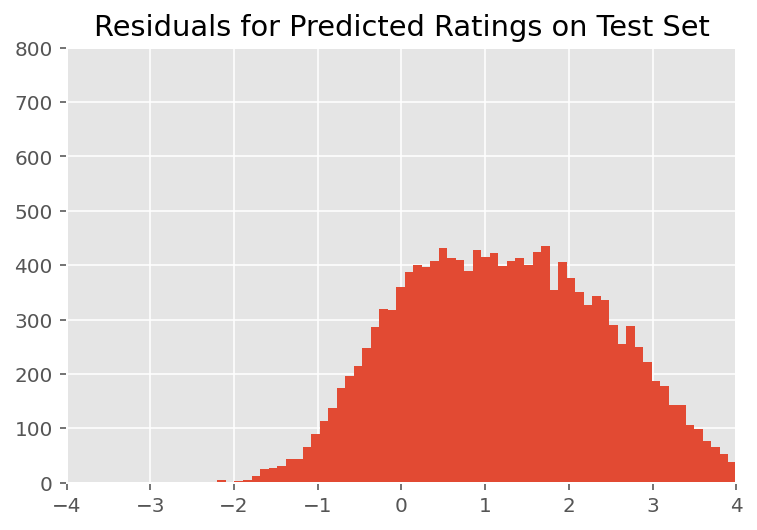
ด้านบน เราติดตั้งโมเดล ตอนนี้เราพิจารณาวิพากษ์วิจารณ์ความเหมาะสมโดยใช้ข้อมูล ซึ่งช่วยให้เราสำรวจและทำความเข้าใจโมเดลได้ดีขึ้น เทคนิคหนึ่งดังกล่าวคือแผนภาพที่เหลือ ซึ่งแสดงความแตกต่างระหว่างการคาดคะเนของแบบจำลองกับความจริงภาคพื้นดินสำหรับจุดข้อมูลแต่ละจุด หากแบบจำลองถูกต้อง ผลต่างควรเป็นแบบกระจายแบบมาตรฐาน การเบี่ยงเบนใด ๆ จากรูปแบบนี้ในโครงเรื่องบ่งชี้ว่าแบบจำลองไม่เหมาะสม

เราสร้างพล็อตที่เหลือโดยสร้างการแจกแจงแบบคาดการณ์หลังการให้คะแนน ซึ่งแทนที่การแจกแจงก่อนหน้าของเอฟเฟกต์แบบสุ่มด้วยข้อมูลการฝึกอบรมที่ได้รับจากด้านหลัง โดยเฉพาะอย่างยิ่ง เราเรียกใช้โมเดลไปข้างหน้าและสกัดกั้นการพึ่งพาเอฟเฟกต์แบบสุ่มก่อนหน้าด้วยวิธีการหลังที่อนุมาน²

lmm_test = lmm_jointdist(features_test)

[
    effect_students_mean,
    effect_instructors_mean,
    effect_departments_mean,
] = [
     np.mean(x, axis=0).astype(np.float32) for x in [
       effect_students_samples,
       effect_instructors_samples,
       effect_departments_samples
       ]
]

# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
    value=(
        effect_students_mean,
        effect_instructors_mean,
        effect_departments_mean,
))

ratings_prediction = ratings_posterior.mean()

เมื่อตรวจสอบด้วยสายตา เศษที่เหลือจะดูค่อนข้างกระจายแบบมาตรฐาน-ปกติ อย่างไรก็ตาม ความพอดีนั้นไม่สมบูรณ์แบบ: มีความน่าจะเป็นมวลในหางมากกว่าการกระจายตัวแบบปกติ ซึ่งบ่งชี้ว่าแบบจำลองอาจปรับปรุงความพอดีโดยการผ่อนคลายสมมติฐานเกี่ยวกับภาวะปกติ

โดยเฉพาะอย่างยิ่งแม้ว่ามันจะเป็นเรื่องธรรมดาที่สุดที่จะใช้การกระจายปกติการจัดอันดับในรุ่น InstEval ชุดข้อมูลมองใกล้ที่ข้อมูลแสดงให้เห็นว่าการให้คะแนนการประเมินผลการเรียนการสอนอยู่ในค่าลำดับความเป็นจริงจาก 1 ถึง 5 ซึ่งแสดงให้เห็นว่าเราควรจะใช้ การแจกแจงแบบมีลำดับ หรือแม้แต่แบบจัดหมวดหมู่ หากเรามีข้อมูลเพียงพอที่จะทิ้งการเรียงลำดับแบบสัมพัทธ์ นี่คือการเปลี่ยนแปลงหนึ่งบรรทัดสำหรับโมเดลด้านบน ใช้รหัสอนุมานเดียวกัน

plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()

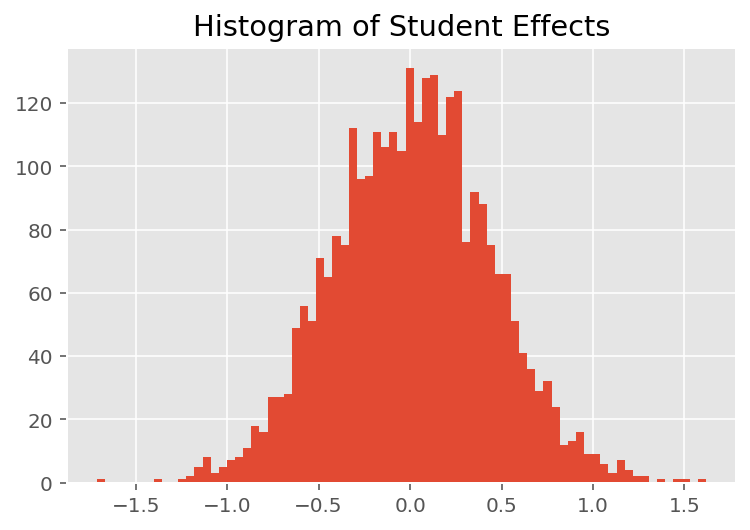
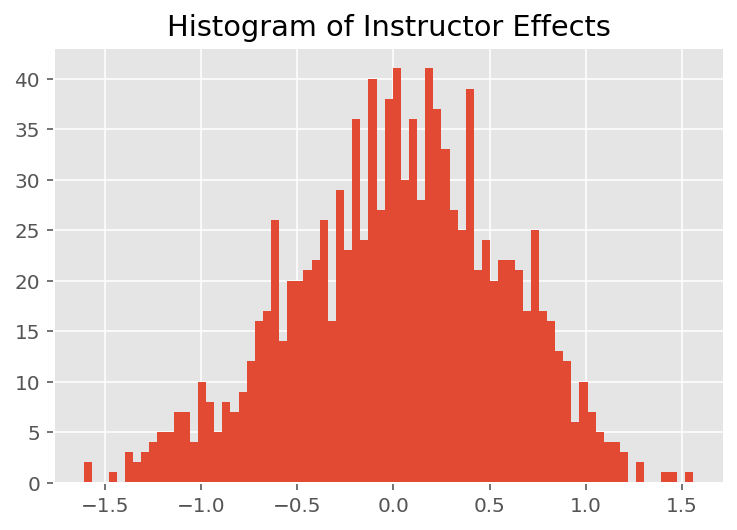
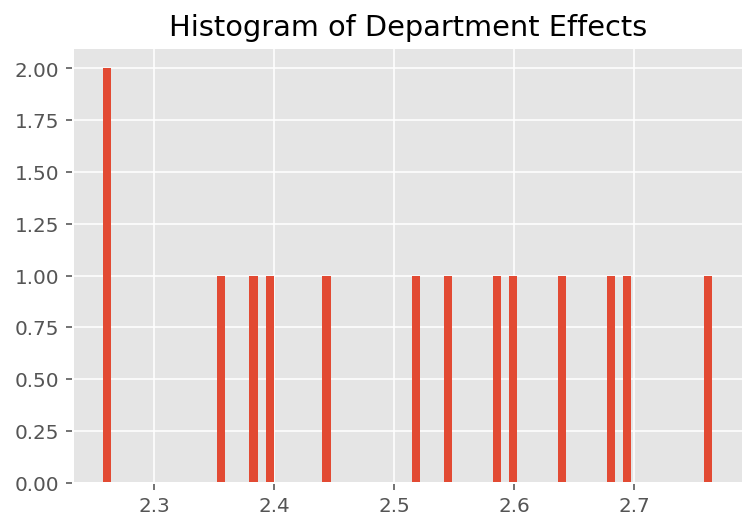
เพื่อสำรวจว่าแบบจำลองทำนายแต่ละบุคคลได้อย่างไร เราดูฮิสโตแกรมของเอฟเฟกต์สำหรับนักเรียน ผู้สอน และแผนก ซึ่งช่วยให้เราเข้าใจว่าแต่ละองค์ประกอบในเวกเตอร์คุณลักษณะของจุดข้อมูลมีแนวโน้มที่จะมีอิทธิพลต่อผลลัพธ์อย่างไร

ไม่น่าแปลกใจเลยที่ด้านล่างนี้ ว่านักเรียนแต่ละคนมีผลเพียงเล็กน้อยต่อคะแนนการประเมินของผู้สอน ที่น่าสนใจคือเราเห็นว่าแผนกที่ผู้สอนสังกัดอยู่มีผลอย่างมาก

plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()

plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()

plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()

เชิงอรรถ

¹ โมเดลเอฟเฟกต์แบบผสมเชิงเส้นเป็นกรณีพิเศษที่เราสามารถวิเคราะห์ความหนาแน่นของส่วนเพิ่มได้ สำหรับจุดประสงค์ของบทช่วยสอนนี้ เราสาธิต Monte Carlo EM ซึ่งนำไปใช้กับความหนาแน่นขอบที่ไม่ใช่การวิเคราะห์ได้ง่ายกว่า เช่น ขยายความเป็นไปได้เป็นแบบจัดหมวดหมู่แทนที่จะเป็นปกติ

² เพื่อความง่าย เราสร้างค่าเฉลี่ยของการแจกแจงแบบคาดการณ์โดยใช้รูปแบบการส่งต่อเพียงครั้งเดียว สิ่งนี้ทำได้โดยการปรับสภาพบนค่าเฉลี่ยหลังและใช้ได้กับโมเดลเอฟเฟกต์แบบผสมเชิงเส้น อย่างไรก็ตาม สิ่งนี้ไม่ถูกต้องโดยทั่วไป: ค่าเฉลี่ยของการแจกแจงแบบทำนายภายหลังนั้นยากโดยทั่วไปและต้องใช้ค่าเฉลี่ยเชิงประจักษ์ในการส่งต่อแบบจำลองหลายครั้งที่ได้รับตัวอย่างหลัง

รับทราบ

กวดวิชานี้ถูกเขียนเดิมในเอ็ดเวิร์ด 1.0 ( แหล่งที่มา ) เราขอขอบคุณผู้ร่วมเขียนข้อความและแก้ไขเวอร์ชันนั้น

อ้างอิง

1. Douglas Bates และ Martin Machler และ Ben Bolker และ Steve Walker การติดตั้งโมเดลลิเนียร์เอฟเฟกต์แบบผสมโดยใช้ lme4 วารสารสถิติซอฟต์แวร์ 67 (1): 1-48 2015

2. Arthur P. Dempster, Nan M. Laird และ Donald B. Rubin โอกาสสูงสุดจากข้อมูลที่ไม่สมบูรณ์ผ่านอัลกอริทึม EM วารสารของสมาคมสถิติรุ่น B (แบบแผน) 1-38 1977

3. แอนดรูว์ เกลแมนและเจนนิเฟอร์ ฮิลล์ การวิเคราะห์ข้อมูลโดยใช้แบบจำลองการถดถอยและหลายระดับ/ลำดับชั้น สำนักพิมพ์มหาวิทยาลัยเคมบริดจ์ 2549

4. เดวิด เอ. ฮาร์วิลล์ แนวทางความเป็นไปได้สูงสุดในการประมาณค่าองค์ประกอบความแปรปรวนและปัญหาที่เกี่ยวข้อง วารสารของสมาคมอเมริกันสถิติ 72 (358): 320-338 1977

5. ไมเคิล ไอ. จอร์แดน. ข้อมูลเบื้องต้นเกี่ยวกับโมเดลกราฟิก รายงานทางเทคนิค พ.ศ. 2546

6. แนน เอ็ม แลร์ด และ เจมส์ แวร์. แบบจำลองเอฟเฟกต์สุ่มสำหรับข้อมูลตามยาว Biometrics, 963-974 1982

7. Greg Wei และ Martin A. Tanner การใช้อัลกอริธึม EM ของ Monte Carlo และอัลกอริธึมการเพิ่มข้อมูลของคนจน วารสารของสมาคมอเมริกันสถิติ 699-704 1990