रैखिक मिश्रित प्रभाव मॉडल

TensorFlow.org पर देखें Google Colab में चलाएं GitHub पर स्रोत देखें नोटबुक डाउनलोड करें

एक रैखिक मिश्रित प्रभाव मॉडल संरचित रैखिक संबंधों के मॉडलिंग के लिए एक सरल दृष्टिकोण है (हारविल, 1997; लैयर्ड एंड वेयर, 1982)। प्रत्येक डेटा बिंदु में अलग-अलग प्रकार के इनपुट होते हैं - समूहों में वर्गीकृत - और एक वास्तविक-मूल्यवान आउटपुट। एक रेखीय मिश्रित प्रभाव मॉडल एक पदानुक्रमित मॉडल है: यह किसी भी अलग-अलग डेटा बिंदु के बारे में अनुमान में सुधार करने के शेयरों समूहों में सांख्यिकीय शक्ति।

इस ट्यूटोरियल में, हम TensorFlow Probability में वास्तविक दुनिया के उदाहरण के साथ रैखिक मिश्रित प्रभाव मॉडल प्रदर्शित करते हैं। हम JointDistributionCoroutine और मार्कोव श्रृंखला मोंटे कार्लो (इस्तेमाल करेंगे tfp.mcmc ) मॉड्यूल।

निर्भरता और पूर्वापेक्षाएँ

आयात और सेट अप

चीजें तेजी से करें!

इससे पहले कि हम इसमें गोता लगाएँ, आइए सुनिश्चित करें कि हम इस डेमो के लिए GPU का उपयोग कर रहे हैं।

ऐसा करने के लिए, "रनटाइम" -> "रनटाइम प्रकार बदलें" -> "हार्डवेयर त्वरक" -> "जीपीयू" चुनें।

निम्नलिखित स्निपेट सत्यापित करेगा कि हमारे पास GPU तक पहुंच है।

if tf.test.gpu_device_name() != '/device:GPU:0':
  print('WARNING: GPU device not found.')
else:
  print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))

SUCCESS: Found GPU: /device:GPU:0

आंकड़े

हम का उपयोग InstEval डेटा लोकप्रिय से सेट lme4 आर में पैकेज (बेट्स एट अल।, 2015)। यह पाठ्यक्रमों का एक डेटा सेट और उनकी मूल्यांकन रेटिंग है। प्रत्येक पाठ्यक्रम जैसे मेटाडेटा students , instructors , और departments , और ब्याज की प्रतिक्रिया चर मूल्यांकन रेटिंग है।

def load_insteval():
  """Loads the InstEval data set.

  It contains 73,421 university lecture evaluations by students at ETH
  Zurich with a total of 2,972 students, 2,160 professors and
  lecturers, and several student, lecture, and lecturer attributes.
  Implementation is built from the `observations` Python package.

  Returns:
    Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
    dictionary `metadata` of column headers (feature names).
  """
  url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
         'lme4/InstEval.csv')
  with requests.Session() as s:
    download = s.get(url)
    f = download.content.decode().splitlines()

  iterator = csv.reader(f)
  columns = next(iterator)[1:]
  x_train = np.array([row[1:] for row in iterator], dtype=np.int)
  metadata = {'columns': columns}
  return x_train, metadata

हम डेटा सेट को लोड और प्रीप्रोसेस करते हैं। हमारे पास 20% डेटा है ताकि हम अनदेखी डेटा बिंदुओं पर अपने फिट किए गए मॉडल का मूल्यांकन कर सकें। नीचे हम पहली कुछ पंक्तियों की कल्पना करते हैं।

data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
                            'd': 'instructors',
                            'dept': 'departments',
                            'y': 'ratings'})
data['students'] -= 1  # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes

train = data.sample(frac=0.8)
test = data.drop(train.index)

train.head()

हम एक के मामले में डेटा सेट की स्थापना की features आदानों की शब्दकोश है और एक labels उत्पादन रेटिंग करने के लिए इसी। प्रत्येक सुविधा को एक पूर्णांक के रूप में एन्कोड किया गया है और प्रत्येक लेबल (मूल्यांकन रेटिंग) को फ्लोटिंग पॉइंट नंबर के रूप में एन्कोड किया गया है।

get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
    k: get_value(train, key=k, dtype=np.int32)
    for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)

features_test = {k: get_value(test, key=k, dtype=np.int32)
                 for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)

num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]

print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)

Number of students: 2972
Number of instructors: 1128
Number of departments: 14
Number of observations: 58737

नमूना

एक विशिष्ट रैखिक मॉडल स्वतंत्रता मानता है, जहां डेटा बिंदुओं के किसी भी जोड़े में एक निरंतर रैखिक संबंध होता है। में InstEval डेटा सेट, टिप्पणियों समूहों, जिनमें से प्रत्येक अलग ढलानों और अवरोध हो सकता है में उत्पन्न होती हैं। रैखिक मिश्रित प्रभाव मॉडल, जिन्हें पदानुक्रमित रैखिक मॉडल या बहुस्तरीय रैखिक मॉडल के रूप में भी जाना जाता है, इस घटना को पकड़ते हैं (जेलमैन एंड हिल, 2006)।

इस घटना के उदाहरणों में शामिल हैं:

  • छात्र। एक छात्र के अवलोकन स्वतंत्र नहीं हैं: कुछ छात्र व्यवस्थित रूप से कम (या उच्च) व्याख्यान रेटिंग दे सकते हैं।
  • अनुदेशकों। एक प्रशिक्षक के अवलोकन स्वतंत्र नहीं हैं: हम उम्मीद करते हैं कि अच्छे शिक्षकों के पास आम तौर पर अच्छी रेटिंग होती है और बुरे शिक्षकों की आम तौर पर खराब रेटिंग होती है।
  • विभागों। एक विभाग के अवलोकन स्वतंत्र नहीं हैं: कुछ विभागों में आमतौर पर सूखी सामग्री या कठोर ग्रेडिंग हो सकती है और इस प्रकार उन्हें दूसरों की तुलना में कम दर्जा दिया जा सकता है।

इस, याद की एक डेटा सेट के लिए है कि कब्जा करने के लिए \(N\times D\) सुविधाओं \(\mathbf{X}\) और \(N\) लेबल \(\mathbf{y}\), रेखीय प्रतीपगमन मानती मॉडल

\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]

जहां एक ढलान वेक्टर है \(\beta\in\mathbb{R}^D\), अवरोधन \(\alpha\in\mathbb{R}\), और यादृच्छिक शोर \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)। हम कहते हैं कि \(\beta\) और \(\alpha\) "निश्चित प्रभाव" कर रहे हैं: वे डेटा बिंदुओं की जनसंख्या भर में आयोजित की निरंतर प्रभाव हैं \((x, y)\)। एक संभावना के रूप में समीकरण का एक बराबर तैयार है \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\)। यह संभावना आदेश की बात का अनुमान है खोजने के लिए अनुमान के दौरान अधिकतम होती है \(\beta\) और \(\alpha\) कि डेटा फिट।

एक रैखिक मिश्रित प्रभाव मॉडल रैखिक प्रतिगमन को इस प्रकार बढ़ाता है

\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]

जहां अभी भी एक ढलान वेक्टर है \(\beta\in\mathbb{R}^P\), अवरोधन \(\alpha\in\mathbb{R}\), और यादृच्छिक शोर \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)। इसके अलावा, एक शब्द है \(\mathbf{Z}\eta\), जहां \(\mathbf{Z}\) एक सुविधाओं मैट्रिक्स और है \(\eta\in\mathbb{R}^Q\) यादृच्छिक ढलानों का एक वेक्टर है; \(\eta\) सामान्य रूप से विचरण घटक पैरामीटर के साथ वितरित किया जाता है \(\sigma^2\)। \(\mathbf{Z}\) मूल विभाजन द्वारा बनाई है \(N\times D\) एक नया करने के मामले में मैट्रिक्स सुविधाओं \(N\times P\) मैट्रिक्स \(\mathbf{X}\) और \(N\times Q\) मैट्रिक्स \(\mathbf{Z}\), जहां \(P + Q=D\)इस विभाजन हमें का उपयोग कर अलग सुविधाओं मॉडल करने के लिए अनुमति देता है: तय प्रभाव \(\beta\) और अव्यक्त चर \(\eta\) क्रमशः।

हम कहते हैं कि अव्यक्त चर \(\eta\) "यादृच्छिक प्रभाव" कर रहे हैं: वे प्रभाव है कि आबादी के हिसाब से भिन्न (हालांकि वे उप-जनसंख्या भर में लगातार हो सकता है) कर रहे हैं। विशेष रूप से, क्योंकि यादृच्छिक प्रभाव \(\eta\) मतलब 0 डेटा लेबल के माध्य से कब्जा कर लिया है है, \(\mathbf{X}\beta + \alpha\)। यादृच्छिक प्रभाव घटक \(\mathbf{Z}\eta\) डेटा में कैप्चर विविधताओं: "। प्रशिक्षक # 54 1.4 अंक मतलब की तुलना में अधिक दर्जा दिया है" उदाहरण के लिए,

इस ट्यूटोरियल में, हम निम्नलिखित प्रभाव प्रस्तुत करते हैं:

  • फिक्स्ड प्रभाव: service । service एक द्विआधारी पाठ्यक्रम प्रशिक्षक के मुख्य विभाग के अंतर्गत आता है कि क्या करने के लिए इसी covariate है। कोई फर्क नहीं पड़ता कि हम कितना अतिरिक्त डेटा एकत्र, यह केवल मूल्यों पर ले जा सकते हैं \(0\) और \(1\)।
  • रैंडम प्रभाव: students , instructors , और departments । पाठ्यक्रम मूल्यांकन रेटिंग की आबादी से अधिक टिप्पणियों को देखते हुए, हम नए छात्रों, शिक्षकों या विभागों को देख सकते हैं।

R के lme4 पैकेज (बेट्स एट अल।, 2015) के सिंटैक्स में, मॉडल को संक्षेप में प्रस्तुत किया जा सकता है

ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1

जहां x अर्थ है एक निश्चित प्रभाव, (1|x) के लिए एक यादृच्छिक प्रभाव को दर्शाता है x , और 1 एक अवरोधन अवधि को दर्शाता है।

हम नीचे इस मॉडल को एक संयुक्त वितरण के रूप में लागू करते हैं। पैरामीटर को ट्रैकिंग के लिए बेहतर समर्थन करवाने के लिए (उदाहरण के लिए, हम सब को ट्रैक करना चाहते tf.Variable में model.trainable_variables , हम के रूप में मॉडल टेम्पलेट लागू) tf.Module ।

class LinearMixedEffectModel(tf.Module):
  def __init__(self):
    # Set up fixed effects and other parameters.
    # These are free parameters to be optimized in E-steps
    self._intercept = tf.Variable(0., name="intercept")            # alpha in eq
    self._effect_service = tf.Variable(0., name="effect_service")  #  beta in eq
    self._stddev_students = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_students")            # sigma in eq
    self._stddev_instructors = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_instructors")         # sigma in eq
    self._stddev_departments = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_departments")         # sigma in eq

  def __call__(self, features):
    model = tfd.JointDistributionSequential([
      # Set up random effects.
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_students),
          scale_identity_multiplier=self._stddev_students),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_instructors),
          scale_identity_multiplier=self._stddev_instructors),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_departments),
          scale_identity_multiplier=self._stddev_departments),
      # This is the likelihood for the observed.
      lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
          tfd.Normal(
              loc=(self._effect_service * features["service"] +
                  tf.gather(effect_students, features["students"], axis=-1) +
                  tf.gather(effect_instructors, features["instructors"], axis=-1) +
                  tf.gather(effect_departments, features["departments"], axis=-1) +
                  self._intercept),
              scale=1.),
              reinterpreted_batch_ndims=1)
    ])

    # To enable tracking of the trainable variables via the created distribution,
    # we attach a reference to `self`. Since all TFP objects sub-class
    # `tf.Module`, this means that the following is possible:
    # LinearMixedEffectModel()(features_train).trainable_variables
    # ==> tuple of all tf.Variables created by LinearMixedEffectModel.
    model._to_track = self
    return model

lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)

lmm_train.trainable_variables

(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)

एक संभाव्य ग्राफिकल प्रोग्राम के रूप में, हम इसके कम्प्यूटेशनल ग्राफ के संदर्भ में मॉडल की संरचना की कल्पना भी कर सकते हैं। यह ग्राफ प्रोग्राम में यादृच्छिक चरों में डेटाफ्लो को एन्कोड करता है, ग्राफिकल मॉडल (जॉर्डन, 2003) के संदर्भ में उनके संबंधों को स्पष्ट करता है।

एक सांख्यिकीय उपकरण के रूप में, हम ग्राफ को क्रम में बेहतर देखने के लिए, उदाहरण के लिए लग सकता है, कि intercept और effect_service सशर्त निर्भर दी हैं ratings ; स्रोत कोड से यह देखना कठिन हो सकता है यदि प्रोग्राम कक्षाओं के साथ लिखा गया है, मॉड्यूल में क्रॉस संदर्भ, और/या सबरूटीन। एक कम्प्यूटेशनल उपकरण के रूप में, हम भी अव्यक्त चर में प्रवाह ध्यान दे सकते हैं ratings के माध्यम से चर tf.gather ऑप्स। यह कुछ हार्डवेयर त्वरक पर एक टोंटी हो सकता है अगर अनुक्रमण Tensor रों महंगा है, ग्राफ को देखने से यह आसानी से स्पष्ट हो जाता है।

lmm_train.resolve_graph()

(('effect_students', ()),
 ('effect_instructors', ()),
 ('effect_departments', ()),
 ('x', ('effect_departments', 'effect_instructors', 'effect_students')))

पैरामीटर अनुमान

डेटा को देखते हुए अनुमान के लक्ष्य मॉडल तय प्रभाव ढलान फिट करने के लिए है \(\beta\), अवरोधन \(\alpha\), और विचरण घटक पैरामीटर \(\sigma^2\)। अधिकतम संभावना सिद्धांत इस कार्य को औपचारिक रूप देता है:

\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]

इस ट्यूटोरियल में, हम इस सीमांत घनत्व को अधिकतम करने के लिए मोंटे कार्लो ईएम एल्गोरिथम का उपयोग करते हैं (डेम्पस्टर एट अल।, 1977; वेई और टैनर, 1990)। यादृच्छिक प्रभाव ("ई-स्टेप"), और हम मापदंडों ("एम-स्टेप") के संबंध में अपेक्षा को अधिकतम करने के लिए ग्रेडिएंट डिसेंट का प्रदर्शन करते हैं:

  • ई-स्टेप के लिए, हमने हैमिल्टनियन मोंटे कार्लो (HMC) की स्थापना की। यह एक वर्तमान स्थिति लेता है - छात्र, प्रशिक्षक, और विभाग प्रभाव - और एक नया राज्य लौटाता है। हम नए राज्य को TensorFlow चर के लिए असाइन करते हैं, जो HMC श्रृंखला की स्थिति को दर्शाएगा।

  • एम-स्टेप के लिए, हम एचएमसी से पश्च नमूने का उपयोग एक स्थिर तक सीमांत संभावना के निष्पक्ष अनुमान की गणना करने के लिए करते हैं। फिर हम इसके ग्रेडिएंट को ब्याज के मापदंडों के संबंध में लागू करते हैं। यह सीमांत संभावना पर एक निष्पक्ष स्टोकेस्टिक वंश कदम पैदा करता है। हम इसे एडम टेन्सरफ्लो ऑप्टिमाइज़र के साथ लागू करते हैं और सीमांत के नकारात्मक को कम करते हैं।

target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]

# For debugging
target_log_prob_fn(*current_state)

<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>

# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=target_log_prob_fn,
    step_size=0.015,
    num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)

@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
  next_state, next_kernel_results = hmc.one_step(
      current_state=current_state,
      previous_kernel_results=kernel_results)
  return next_state, next_kernel_results

optimizer = tf.optimizers.Adam(learning_rate=.01)

# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
  with tf.GradientTape() as tape:
    loss = -target_log_prob_fn(*current_state)
  grads = tape.gradient(loss, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss

हम एक वार्म-अप चरण करते हैं, जो कई पुनरावृत्तियों के लिए एक एमसीएमसी श्रृंखला चलाता है ताकि प्रशिक्षण को पोस्टीरियर की संभाव्यता द्रव्यमान के भीतर शुरू किया जा सके। फिर हम एक प्रशिक्षण लूप चलाते हैं। यह संयुक्त रूप से ई और एम-स्टेप्स चलाता है और प्रशिक्षण के दौरान मूल्यों को रिकॉर्ड करता है।

num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])

# Run warm-up stage.
for t in range(num_warmup_iters):
  current_state, kernel_results = one_e_step(current_state, kernel_results)
  num_accepted += kernel_results.is_accepted.numpy()
  if t % 500 == 0 or t == num_warmup_iters - 1:
    print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
        t, num_accepted / (t + 1)))

num_accepted = 0  # reset acceptance rate counter

# Run training.
for t in range(num_iters):
  # run 5 MCMC iterations before every joint EM update
  for _ in range(5):
    current_state, kernel_results = one_e_step(current_state, kernel_results)
  loss = one_m_step(current_state)
  effect_students_samples[t, :] = current_state[0].numpy()
  effect_instructors_samples[t, :] = current_state[1].numpy()
  effect_departments_samples[t, :] = current_state[2].numpy()
  num_accepted += kernel_results.is_accepted.numpy()
  loss_history[t] = loss.numpy()
  if t % 500 == 0 or t == num_iters - 1:
    print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
        t, num_accepted / (t + 1), loss_history[t]))

Warm-Up Iteration:   0 Acceptance Rate: 1.000
Warm-Up Iteration: 500 Acceptance Rate: 0.754
Warm-Up Iteration: 999 Acceptance Rate: 0.707
Iteration:    0 Acceptance Rate: 1.000 Loss: 98220.266
Iteration:  500 Acceptance Rate: 0.703 Loss: 96003.969
Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609
Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891

तुम भी एक में के लिए लूप वार्मअप लिख सकते हैं tf.while_loop , और एक में प्रशिक्षण कदम tf.scan या tf.while_loop भी तेजी से अनुमान के लिए। उदाहरण के लिए:

@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
  _, next_state, next_kernel_results = tf.while_loop(
      cond=lambda i, state, pkr: i < k,
      body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
      loop_vars=(tf.constant(0), current_state, kernel_results)
  )
  return next_state, next_kernel_results

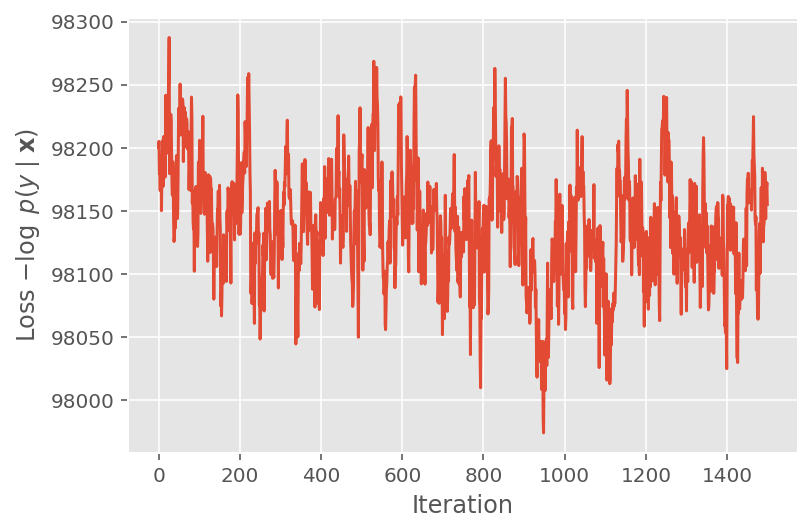
ऊपर, हमने तब तक एल्गोरिथम नहीं चलाया जब तक कि एक अभिसरण सीमा का पता नहीं चला। यह जांचने के लिए कि क्या प्रशिक्षण समझदार था, हम सत्यापित करते हैं कि हानि फ़ंक्शन वास्तव में प्रशिक्षण पुनरावृत्तियों पर अभिसरण करता है।

plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()

पीएनजी

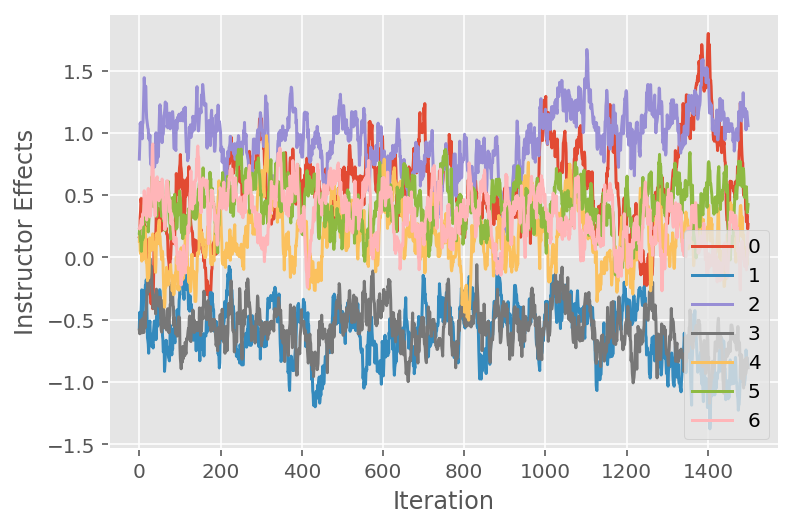
हम एक ट्रेस प्लॉट का भी उपयोग करते हैं, जो विशिष्ट अव्यक्त आयामों में मार्कोव श्रृंखला मोंटे कार्लो एल्गोरिथम के प्रक्षेपवक्र को दर्शाता है। नीचे हम देखते हैं कि विशिष्ट प्रशिक्षक प्रभाव वास्तव में सार्थक रूप से अपनी प्रारंभिक अवस्था से दूर हो जाते हैं और राज्य स्थान का पता लगाते हैं। ट्रेस प्लॉट यह भी इंगित करता है कि प्रभाव प्रशिक्षकों में भिन्न होता है लेकिन समान मिश्रण व्यवहार के साथ।

for i in range(7):
  plt.plot(effect_instructors_samples[:, i])

plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()

पीएनजी

आलोचना

ऊपर, हमने मॉडल फिट किया। अब हम डेटा का उपयोग करके इसके फिट होने की आलोचना करते हैं, जिससे हमें मॉडल का पता लगाने और बेहतर ढंग से समझने की सुविधा मिलती है। ऐसी ही एक तकनीक एक अवशिष्ट प्लॉट है, जो प्रत्येक डेटा बिंदु के लिए मॉडल की भविष्यवाणियों और जमीनी सच्चाई के बीच अंतर को प्लॉट करता है। यदि मॉडल सही थे, तो उनका अंतर सामान्य रूप से वितरित मानक होना चाहिए; प्लॉट में इस पैटर्न से कोई भी विचलन मॉडल मिसफिट का संकेत देता है।

हम पहले रेटिंग पर पोस्टीरियर प्रेडिक्टिव डिस्ट्रीब्यूशन बनाकर अवशिष्ट प्लॉट का निर्माण करते हैं, जो इसके पश्च दिए गए प्रशिक्षण डेटा के साथ यादृच्छिक प्रभावों पर पूर्व वितरण को बदल देता है। विशेष रूप से, हम मॉडल को आगे चलाते हैं और पूर्व यादृच्छिक प्रभावों पर इसकी निर्भरता को उनके अनुमानित पश्च माध्यम से रोकते हैं।²

lmm_test = lmm_jointdist(features_test)

[
    effect_students_mean,
    effect_instructors_mean,
    effect_departments_mean,
] = [
     np.mean(x, axis=0).astype(np.float32) for x in [
       effect_students_samples,
       effect_instructors_samples,
       effect_departments_samples
       ]
]

# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
    value=(
        effect_students_mean,
        effect_instructors_mean,
        effect_departments_mean,
))

ratings_prediction = ratings_posterior.mean()

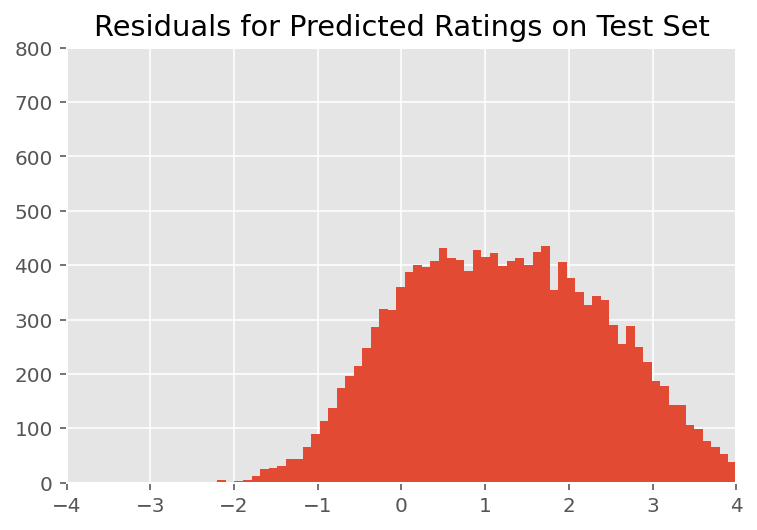
दृश्य निरीक्षण पर, अवशेष कुछ हद तक मानक-सामान्य रूप से वितरित दिखते हैं। हालांकि, फिट सही नहीं है: सामान्य वितरण की तुलना में पूंछ में बड़ा संभावना द्रव्यमान होता है, जो इंगित करता है कि मॉडल अपनी सामान्यता धारणाओं को आराम से अपने फिट में सुधार कर सकता है।

विशेष रूप से, हालांकि यह सबसे में मॉडल रेटिंग के लिए एक सामान्य वितरण उपयोग आम है InstEval डेटा सेट, डेटा को नज़दीक से देखने से पता चलता है कि पाठ्यक्रम मूल्यांकन रेटिंग्स यह पता चलता है कि हम का उपयोग करना चाहिए 1 से 5 के लिए तथ्य यह है क्रमसूचक मूल्यों में हैं एक क्रमिक वितरण, या यहाँ तक कि श्रेणीबद्ध यदि हमारे पास सापेक्ष क्रम को दूर करने के लिए पर्याप्त डेटा है। यह उपरोक्त मॉडल में एक-पंक्ति परिवर्तन है; एक ही अनुमान कोड लागू होता है।

plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()

पीएनजी

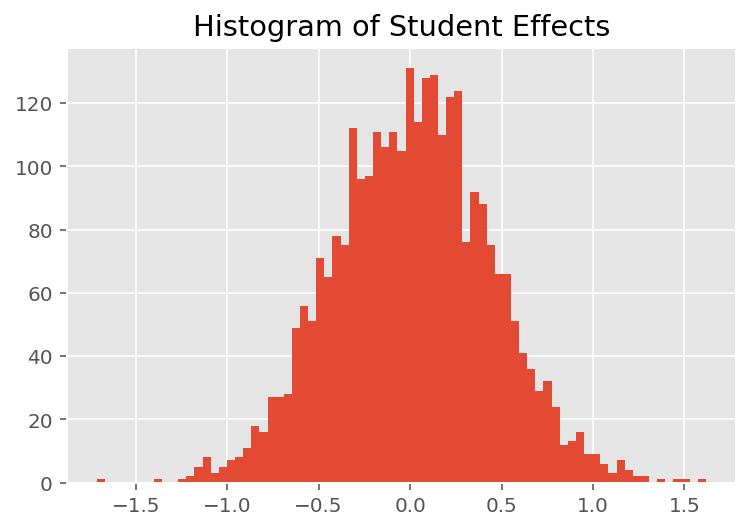
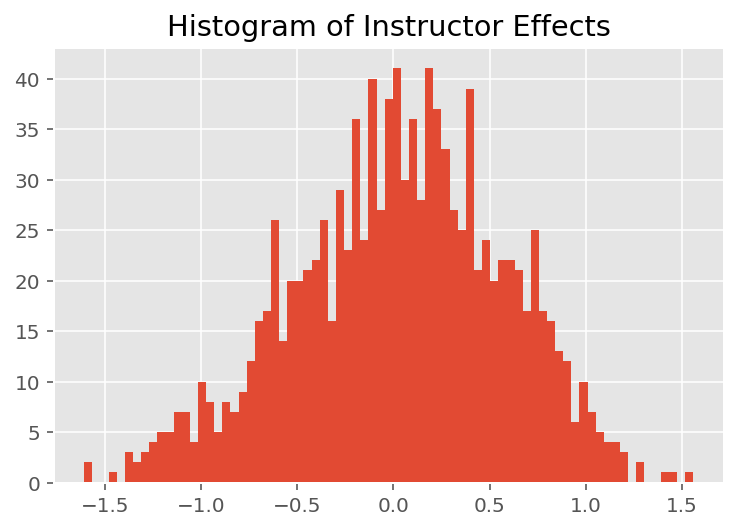
यह पता लगाने के लिए कि मॉडल व्यक्तिगत भविष्यवाणियां कैसे करता है, हम छात्रों, प्रशिक्षकों और विभागों के प्रभावों के हिस्टोग्राम को देखते हैं। इससे हमें यह समझने में मदद मिलती है कि डेटा बिंदु के फीचर वेक्टर में अलग-अलग तत्व कैसे परिणाम को प्रभावित करते हैं।

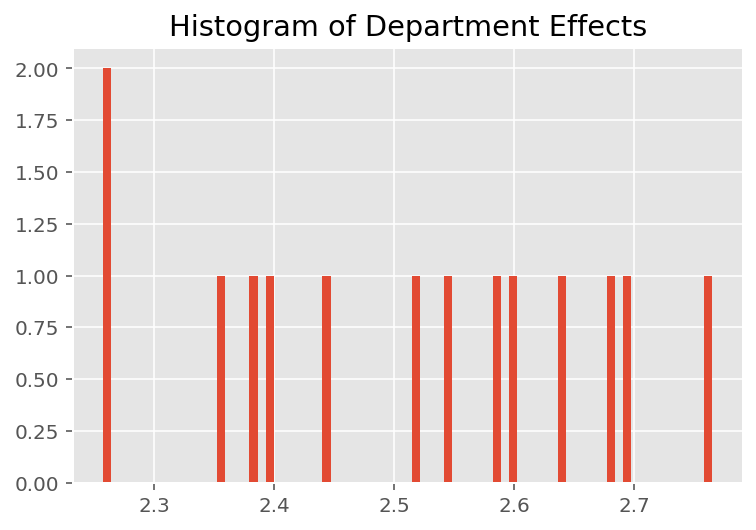
आश्चर्य की बात नहीं है, हम नीचे देखते हैं कि प्रत्येक छात्र आमतौर पर प्रशिक्षक की मूल्यांकन रेटिंग पर बहुत कम प्रभाव डालता है। दिलचस्प बात यह है कि हम देखते हैं कि जिस विभाग का प्रशिक्षक होता है उसका बहुत बड़ा प्रभाव होता है।

plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()

पीएनजी

plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()

पीएनजी

plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()

पीएनजी

फुटनोट

रैखिक मिश्रित प्रभाव मॉडल एक विशेष मामला है जहां हम विश्लेषणात्मक रूप से इसके सीमांत घनत्व की गणना कर सकते हैं। इस ट्यूटोरियल के प्रयोजनों के लिए, हम मोंटे कार्लो ईएम प्रदर्शित करते हैं, जो गैर-विश्लेषणात्मक सीमांत घनत्वों पर अधिक आसानी से लागू होता है जैसे कि सामान्य के बजाय श्रेणीबद्ध होने की संभावना बढ़ा दी गई थी।

सादगी के लिए, हम मॉडल के केवल एक फॉरवर्ड पास का उपयोग करके भविष्य कहनेवाला वितरण का मतलब बनाते हैं। यह पश्च माध्य पर कंडीशनिंग द्वारा किया जाता है और रैखिक मिश्रित प्रभाव मॉडल के लिए मान्य है। हालांकि, यह सामान्य रूप से मान्य नहीं है: पोस्टीरियर प्रेडिक्टिव डिस्ट्रीब्यूशन का मतलब आम तौर पर अट्रैक्टिव होता है और इसके लिए पश्च नमूने दिए गए मॉडल के कई फॉरवर्ड पास में अनुभवजन्य माध्य लेने की आवश्यकता होती है।

स्वीकृतियाँ

इस ट्यूटोरियल मूल रूप से एडवर्ड 1.0 (में लिखा गया था स्रोत )। हम उस संस्करण को लिखने और संशोधित करने के लिए सभी योगदानकर्ताओं को धन्यवाद देते हैं।

संदर्भ

  1. डगलस बेट्स और मार्टिन मचलर और बेन बोल्कर और स्टीव वॉकर। lme4 का उपयोग करते हुए रैखिक मिश्रित-प्रभाव वाले मॉडल की फिटिंग। सांख्यिकीय सॉफ्टवेयर, 67 के जर्नल (1): 1-48, 2015।

  2. आर्थर पी. डेम्पस्टर, नान एम. लैयर्ड, और डोनाल्ड बी. रुबिन। ईएम एलगोरिद्म द्वारा आंशिक डेटा से अधिकतम संभावना है। रॉयल सांख्यिकीय सोसायटी के जर्नल, श्रृंखला बी (Methodological), 1-38, 1977।

  3. एंड्रयू जेलमैन और जेनिफर हिल। प्रतिगमन और बहुस्तरीय/पदानुक्रमित मॉडल का उपयोग करके डेटा विश्लेषण। कैम्ब्रिज यूनिवर्सिटी प्रेस, 2006।

  4. डेविड ए हार्विल। विचरण घटक अनुमान और संबंधित समस्याओं के लिए अधिकतम संभावना दृष्टिकोण। अमेरिकी सांख्यिकीय एसोसिएशन के जर्नल, 72 (358): 320-338, 1977।

  5. माइकल आई। जॉर्डन। ग्राफिकल मॉडल का परिचय। तकनीकी रिपोर्ट, 2003।

  6. नान एम. लैयर्ड और जेम्स वेयर। अनुदैर्ध्य डेटा के लिए यादृच्छिक-प्रभाव मॉडल। बॉयोमेट्रिक्स 963-974, 1982।

  7. ग्रेग वेई और मार्टिन ए. टान्नर। ईएम एल्गोरिथम का एक मोंटे कार्लो कार्यान्वयन और गरीब आदमी का डेटा वृद्धि एल्गोरिदम। अमेरिकी सांख्यिकीय एसोसिएशन के जर्नल, 699-704, 1990।