מודלים של אפקטים מעורבים ליניאריים

הצג באתר TensorFlow.org

הפעל בגוגל קולאב

צפה במקור ב-GitHub

הורד מחברת

מודל ליניארי של אפקטים מעורבים הוא גישה פשוטה למודל של קשרים ליניאריים מובנים (Harville, 1997; Laird and Ware, 1982). כל נקודת נתונים מורכבת מתשומות מסוגים שונים - מסווגים לקבוצות - ופלט בעל ערך אמיתי. מודל השפעות מעורבות ליניארי הוא מודל הירארכי: הוא שותף כוח סטטיסטי בין הקבוצות על מנת לשפר מסקנות לגבי כל נקודת נתונים יחיד.

במדריך זה, אנו מדגימים מודלים של אפקטים מעורבים ליניאריים עם דוגמה מהעולם האמיתי ב- TensorFlow Probability. אנו נשתמש שרשרת JointDistributionCoroutine ו מרקוב מונטה קרלו ( tfp.mcmc מודולים).

תלות ותנאים מוקדמים

ייבוא ​​והגדרות

import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp

tfd = tfp.distributions
tfb = tfp.bijectors

dtype = tf.float64

%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')

הפוך דברים מהר!

לפני שנצלול פנימה, בואו נוודא שאנחנו משתמשים ב-GPU עבור הדגמה זו.

כדי לעשות זאת, בחר "זמן ריצה" -> "שנה סוג זמן ריצה" -> "מאיץ חומרה" -> "GPU".

הקטע הבא יאמת שיש לנו גישה ל-GPU.

if tf.test.gpu_device_name() != '/device:GPU:0':
  print('WARNING: GPU device not found.')
else:
  print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))

SUCCESS: Found GPU: /device:GPU:0

נתונים

אנו משתמשים InstEval נתונים לקבוע מן פופולרי lme4 החבילה ב R (בייטס et al., 2015). זהו מערך נתונים של קורסים ודירוגי ההערכה שלהם. כל קורס כולל metadata כגון students , instructors , וכן departments , ואת המשתנה בריבית בתגובה הוא הדירוג הערכה.

def load_insteval():
  """Loads the InstEval data set.

  It contains 73,421 university lecture evaluations by students at ETH
  Zurich with a total of 2,972 students, 2,160 professors and
  lecturers, and several student, lecture, and lecturer attributes.
  Implementation is built from the `observations` Python package.

  Returns:
    Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
    dictionary `metadata` of column headers (feature names).
  """
  url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
         'lme4/InstEval.csv')
  with requests.Session() as s:
    download = s.get(url)
    f = download.content.decode().splitlines()

  iterator = csv.reader(f)
  columns = next(iterator)[1:]
  x_train = np.array([row[1:] for row in iterator], dtype=np.int)
  metadata = {'columns': columns}
  return x_train, metadata

אנו טוענים ומעבדים מראש את מערך הנתונים. אנו מחזיקים 20% מהנתונים כדי שנוכל להעריך את המודל המותאם שלנו על נקודות נתונים בלתי נראות. להלן אנו מדמיינים את השורות הראשונות.

data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
                            'd': 'instructors',
                            'dept': 'departments',
                            'y': 'ratings'})
data['students'] -= 1  # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes

train = data.sample(frac=0.8)
test = data.drop(train.index)

train.head()

הקמנו מערך נתון במונחים של features מילון התשומות לבין labels פלט מתאים הרייטינג. כל תכונה מקודדת כמספר שלם וכל תווית (דירוג הערכה) מקודדת כמספר נקודה צפה.

get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
    k: get_value(train, key=k, dtype=np.int32)
    for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)

features_test = {k: get_value(test, key=k, dtype=np.int32)
                 for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)

num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]

print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)

Number of students: 2972
Number of instructors: 1128
Number of departments: 14
Number of observations: 58737

דֶגֶם

מודל ליניארי טיפוסי מניח עצמאות, כאשר לכל זוג נקודות נתונים יש קשר ליניארי קבוע. בשנות ה InstEval סט נתונים, תצפיות להתעורר בקבוצות שכל אחת מהן עשויה להיות מדרונות מיירט משתנים. מודלים של אפקטים מעורבים ליניאריים, הידועים גם כמודלים ליניאריים היררכיים או מודלים ליניאריים מרובי-שכבות, לוכדים תופעה זו (Gelman & Hill, 2006).

דוגמאות לתופעה זו כוללות:

• סטודנטים. תצפיות של סטודנט אינן עצמאיות: חלק מהסטודנטים עשויים לתת באופן שיטתי דירוגי הרצאה נמוכים (או גבוהים).
• מדריכים. תצפיות של מדריך אינן עצמאיות: אנו מצפים שלמורים טובים יהיו בדרך כלל דירוגים טובים ולמורים גרועים בדרך כלל דירוג גרוע.
• מחלקות. תצפיות ממחלקה אינן עצמאיות: מחלקות מסוימות עשויות להיות בדרך כלל עם חומר יבש או דירוג מחמיר יותר, ובכך להיות מדורגות נמוך יותר מאחרות.

כדי ללכוד זה, נזכיר כי עבור קבוצת נתונים של \(N\times D\) תכונות \(\mathbf{X}\) ו \(N\) תוויות \(\mathbf{y}\), טוען רגרסיה ליניארית מודל

\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]

איפה קיים וקטור מדרון \(\beta\in\mathbb{R}^D\), יירוט \(\alpha\in\mathbb{R}\), ורעשים אקראיים \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). אנו אומרים כי \(\beta\) ו \(\alpha\) הם "תופעות קבוע": הם תופעות קבועים ברחבי האוכלוסייה של נקודות נתונים \((x, y)\). ניסוח שווה ערך של המשוואה כמו סבירות הוא \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\). הסבירות זה מוגדל במהלך היסק כדי למצוא הערכות נקודת \(\beta\) ו \(\alpha\) שמתאימים את הנתונים.

מודל ליניארי של אפקטים מעורבים מרחיב רגרסיה לינארית כמו

\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]

איפה יש עדיין וקטור מדרון \(\beta\in\mathbb{R}^P\), יירוט \(\alpha\in\mathbb{R}\), ורעשים אקראיים \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\). בנוסף, קיים מונח \(\mathbf{Z}\eta\), שבו \(\mathbf{Z}\) הוא מטריצת תכונות \(\eta\in\mathbb{R}^Q\) הוא וקטור של מדרון אקראיים; \(\eta\) מתפלג נורמלי עם פרמטר המרכיב שונה \(\sigma^2\). \(\mathbf{Z}\) נוצר על ידי חלוקת המקורי \(N\times D\) מטריקס תכונות במונחים של חדשות \(N\times P\) מטריקס \(\mathbf{X}\) ו \(N\times Q\) מטריקס \(\mathbf{Z}\), שבו \(P + Q=D\): מחיצה זו מאפשרת לנו ליצור דגמים מהתכונות בנפרד באמצעות ההשפעות קבוע \(\beta\) ואת המשתנה הסמוי \(\eta\) בהתאמה.

אנחנו אומרים משתנים חבויים \(\eta\) הם "תופעות אקראיות": הם תופעות המשתנים בין האוכלוסייה (למרות שהם עשויים להיות קבועה על פני תת-אוכלוסיות). בפרט, בגלל ההשפעות האקראיות \(\eta\) יש ממוצע 0, הממוצע של תווית הנתונים הוא נתפס על ידי \(\mathbf{X}\beta + \alpha\). ההשפעות האקראיות מרכיב \(\mathbf{Z}\eta\) לוכד וריאציות נתון: "מדריך # 54 הוא דורג 1.4 נק' גבוהות יותר מהממוצע", למשל,

במדריך זה, אנו מציבים את ההשפעות הבאות:

• תופעות קבוע: service . service הוא covariate בינארי המתאים אם כמובן שייך למחלקת העיקרית של המאמן. לא משנה כמה נתונים נוספים שאנו אוספים, זה יכול לקחת רק על ערכים \(0\) ו \(1\).
• תופעות אקראיות: students , instructors , וכן departments . בהתחשב בתצפיות נוספות מאוכלוסיית הדירוגים של הערכת קורסים, ייתכן שאנו מסתכלים על תלמידים, מורים או מחלקות חדשים.

בתחביר של חבילת lme4 של R (Bates et al., 2015), ניתן לסכם את המודל כ

ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1

איפה x מציין השפעה קבועה, (1|x) מציין אפקט אקראי x , ו- 1 מציין מונח יירוט.

אנו מיישמים מודל זה להלן כהפצה משותפת. כדי לקבל תמיכה טובה יותר עבור מעקב פרמטר (למשל, אנחנו רוצים לעקוב אחר כל tf.Variable ב model.trainable_variables ), אנו ליישם את התבנית המודל כפי tf.Module .

class LinearMixedEffectModel(tf.Module):
  def __init__(self):
    # Set up fixed effects and other parameters.
    # These are free parameters to be optimized in E-steps
    self._intercept = tf.Variable(0., name="intercept")            # alpha in eq
    self._effect_service = tf.Variable(0., name="effect_service")  #  beta in eq
    self._stddev_students = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_students")            # sigma in eq
    self._stddev_instructors = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_instructors")         # sigma in eq
    self._stddev_departments = tfp.util.TransformedVariable(
        1., bijector=tfb.Exp(), name="stddev_departments")         # sigma in eq

  def __call__(self, features):
    model = tfd.JointDistributionSequential([
      # Set up random effects.
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_students),
          scale_identity_multiplier=self._stddev_students),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_instructors),
          scale_identity_multiplier=self._stddev_instructors),
      tfd.MultivariateNormalDiag(
          loc=tf.zeros(num_departments),
          scale_identity_multiplier=self._stddev_departments),
      # This is the likelihood for the observed.
      lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
          tfd.Normal(
              loc=(self._effect_service * features["service"] +
                  tf.gather(effect_students, features["students"], axis=-1) +
                  tf.gather(effect_instructors, features["instructors"], axis=-1) +
                  tf.gather(effect_departments, features["departments"], axis=-1) +
                  self._intercept),
              scale=1.),
              reinterpreted_batch_ndims=1)
    ])

    # To enable tracking of the trainable variables via the created distribution,
    # we attach a reference to `self`. Since all TFP objects sub-class
    # `tf.Module`, this means that the following is possible:
    # LinearMixedEffectModel()(features_train).trainable_variables
    # ==> tuple of all tf.Variables created by LinearMixedEffectModel.
    model._to_track = self
    return model

lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)

lmm_train.trainable_variables

(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>,
 <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)

כתוכנית גרפית הסתברותית, אנו יכולים גם לדמיין את מבנה המודל במונחים של הגרף החישובי שלו. גרף זה מקודד זרימת נתונים על פני המשתנים האקראיים בתוכנית, ומבהיר את הקשרים ביניהם במונחים של מודל גרפי (Jordan, 2003).

ככלי סטטיסטי, נוכל להסתכל בגרף כדי להיטיב לראות, למשל, כי intercept ו effect_service תלוי נתון תנאי ratings ; זה עשוי להיות קשה יותר לראות מקוד המקור אם התוכנית כתובה עם מחלקות, הפניות צולבות בין מודולים ו/או תתי שגרות. ככלי חישובית, נוכל גם להבחין משתנים חבויים לזרום לתוך ratings משתנה באמצעות tf.gather Ops. זה יכול להיות צוואר בקבוק על מאיצי חומרה מסוימים אם לאינדקס Tensor הים הוא יקר; הדמיה של הגרף הופכת את זה לברור.

lmm_train.resolve_graph()

(('effect_students', ()),
 ('effect_instructors', ()),
 ('effect_departments', ()),
 ('x', ('effect_departments', 'effect_instructors', 'effect_students')))

הערכת פרמטר

בהינתן נתונים, המטרה של היקש היא להתאים את שיפוע תופעות קבוע של המודל \(\beta\)יירוט, \(\alpha\)פרמטר רכיב, ושונות \(\sigma^2\). עקרון הסבירות המקסימלית מייסד משימה זו כ

\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]

במדריך זה, אנו משתמשים באלגוריתם Monte Carlo EM כדי למקסם את הצפיפות השולית הזו (Dempster et al., 1977; Wei and Tanner, 1990).¹ אנו מבצעים את רשת Markov Monte Carlo כדי לחשב את הציפייה לסבירות המותנית ביחס ל- אפקטים אקראיים ("E-step"), ואנו מבצעים ירידה בשיפוע כדי למקסם את הציפייה ביחס לפרמטרים ("M-step"):

• עבור המדרגה E, הגדרנו את המילטון מונטה קרלו (HMC). זה לוקח מצב נוכחי - השפעות התלמיד, המדריך והמחלקה - ומחזיר מצב חדש. אנו מקצים את המצב החדש למשתני TensorFlow, אשר יציינו את המצב של שרשרת HMC.

• עבור M-step, אנו משתמשים במדגם האחורי מ-HMC כדי לחשב אומדן חסר פניות של הסבירות השולית עד קבוע. לאחר מכן אנו מיישמים את השיפוע שלו ביחס לפרמטרים של עניין. זה מייצר צעד ירידה סטוכסטי בלתי משוחד על הסבירות השולית. אנו מיישמים את זה עם אופטימיזציית Adam TensorFlow ומצמצמים את השלילי של השולי.

target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]

# For debugging
target_log_prob_fn(*current_state)

<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>

# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=target_log_prob_fn,
    step_size=0.015,
    num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)

@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
  next_state, next_kernel_results = hmc.one_step(
      current_state=current_state,
      previous_kernel_results=kernel_results)
  return next_state, next_kernel_results

optimizer = tf.optimizers.Adam(learning_rate=.01)

# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
  with tf.GradientTape() as tape:
    loss = -target_log_prob_fn(*current_state)
  grads = tape.gradient(loss, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss

אנו מבצעים שלב חימום, המריץ שרשרת MCMC אחת במשך מספר איטרציות, כך שניתן לאתחל את האימון בתוך מסת ההסתברות האחורית. לאחר מכן אנו מפעילים לולאת אימון. הוא מריץ במשותף את שלבי E ו-M ומתעד ערכים במהלך האימון.

num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])

# Run warm-up stage.
for t in range(num_warmup_iters):
  current_state, kernel_results = one_e_step(current_state, kernel_results)
  num_accepted += kernel_results.is_accepted.numpy()
  if t % 500 == 0 or t == num_warmup_iters - 1:
    print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
        t, num_accepted / (t + 1)))

num_accepted = 0  # reset acceptance rate counter

# Run training.
for t in range(num_iters):
  # run 5 MCMC iterations before every joint EM update
  for _ in range(5):
    current_state, kernel_results = one_e_step(current_state, kernel_results)
  loss = one_m_step(current_state)
  effect_students_samples[t, :] = current_state[0].numpy()
  effect_instructors_samples[t, :] = current_state[1].numpy()
  effect_departments_samples[t, :] = current_state[2].numpy()
  num_accepted += kernel_results.is_accepted.numpy()
  loss_history[t] = loss.numpy()
  if t % 500 == 0 or t == num_iters - 1:
    print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
        t, num_accepted / (t + 1), loss_history[t]))

Warm-Up Iteration:   0 Acceptance Rate: 1.000
Warm-Up Iteration: 500 Acceptance Rate: 0.754
Warm-Up Iteration: 999 Acceptance Rate: 0.707
Iteration:    0 Acceptance Rate: 1.000 Loss: 98220.266
Iteration:  500 Acceptance Rate: 0.703 Loss: 96003.969
Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609
Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891

אתה יכול גם לכתוב את החימום עבור לולאה לתוך tf.while_loop , וצעד ההכשרה לתוך tf.scan או tf.while_loop אפילו עבור היקש מהר. לדוגמה:

@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
  _, next_state, next_kernel_results = tf.while_loop(
      cond=lambda i, state, pkr: i < k,
      body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
      loop_vars=(tf.constant(0), current_state, kernel_results)
  )
  return next_state, next_kernel_results

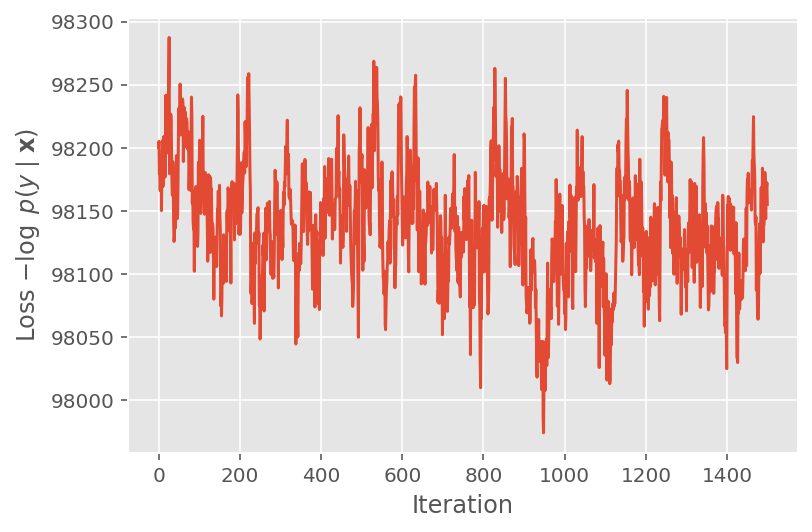
למעלה, לא הרצנו את האלגוריתם עד שזוהה סף התכנסות. כדי לבדוק אם האימון היה הגיוני, אנו מוודאים שפונקציית ההפסד אכן נוטה להתכנס על פני איטרציות אימון.

plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()

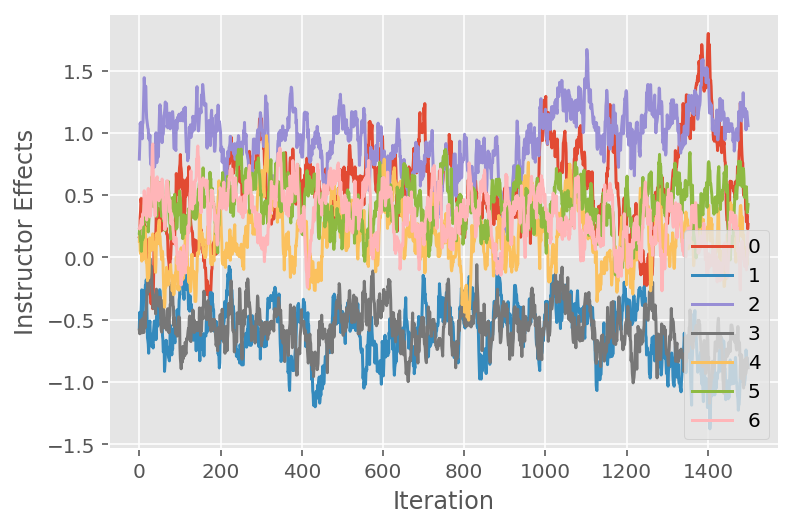
אנו משתמשים גם בעלילת עקבות, המציגה את מסלול האלגוריתם של שרשרת מרקוב מונטה קרלו על פני ממדים סמויים ספציפיים. להלן אנו רואים שאפקטים ספציפיים של מדריך אכן עוברים באופן משמעותי מהמצב ההתחלתי שלהם וחוקרים את מרחב המצב. עלילת העקבות גם מצביעה על כך שהאפקטים שונים בין המדריכים אך עם התנהגות ערבוב דומה.

for i in range(7):
  plt.plot(effect_instructors_samples[:, i])

plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()

ביקורת

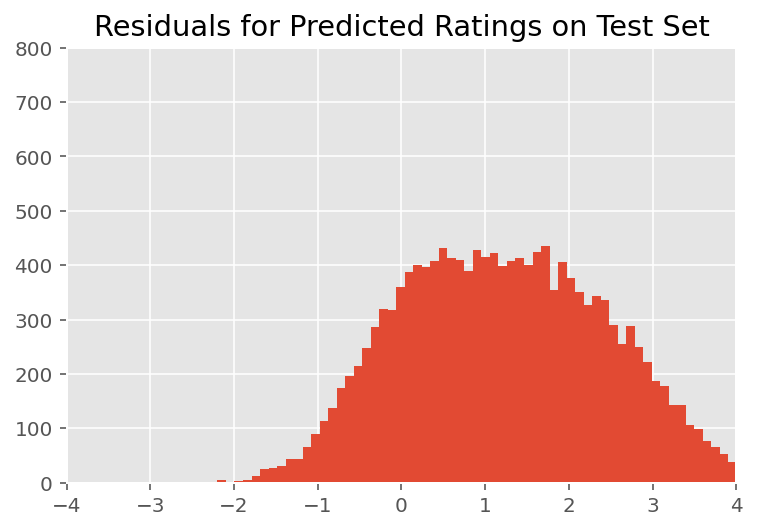
למעלה, התאמנו את הדגם. כעת אנו בוחנים ביקורת על התאמתו באמצעות נתונים, המאפשרים לנו לחקור ולהבין טוב יותר את המודל. טכניקה אחת כזו היא עלילה שיורית, אשר משרטטת את ההבדל בין תחזיות המודל והאמת הבסיסית עבור כל נקודת נתונים. אם המודל היה נכון, ההבדל ביניהם צריך להיות סטנדרטי בחלוקה נורמלית; כל סטייה מהתבנית הזו בעלילה מעידה על חוסר התאמה של הדגם.

אנו בונים את העלילה השיורית על ידי יצירת התפלגות הניבוי האחורית על דירוגים, אשר מחליפה את ההתפלגות הקודמת על ההשפעות האקראיות בנתוני האימון האחוריים שלה. בפרט, אנו מריצים את המודל קדימה ומיירטים את התלות שלו בהשפעות אקראיות קודמות עם האמצעים האחוריים המשוערים שלהם.²

lmm_test = lmm_jointdist(features_test)

[
    effect_students_mean,
    effect_instructors_mean,
    effect_departments_mean,
] = [
     np.mean(x, axis=0).astype(np.float32) for x in [
       effect_students_samples,
       effect_instructors_samples,
       effect_departments_samples
       ]
]

# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
    value=(
        effect_students_mean,
        effect_instructors_mean,
        effect_departments_mean,
))

ratings_prediction = ratings_posterior.mean()

בבדיקה ויזואלית, השאריות נראות מפוזרות במידת מה סטנדרטית-נורמלית. עם זאת, ההתאמה אינה מושלמת: יש מסת הסתברות גדולה יותר בזנבות מאשר התפלגות נורמלית, מה שמצביע על כך שהדגם עשוי לשפר את ההתאמה שלו על ידי הרפיה של הנחות הנורמליות שלו.

בפרט, למרות שהוא נפוץ ביותר להשתמש התפלגות נורמלית לדירוג מודל ב InstEval סט הנתונים, מבט מקרוב על נתון מגלה כי רייטינג ההערכה כמובן הם בערכים סִדוּרִי למעשה מ -1 עד 5. הדבר מצביע על כך שאנחנו צריכים להשתמש התפלגות סידורית, או אפילו קטגורית אם יש לנו מספיק נתונים כדי לזרוק את הסדר היחסי. זהו שינוי בשורה אחת לדגם שלמעלה; אותו קוד מסקנות ישים.

plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()

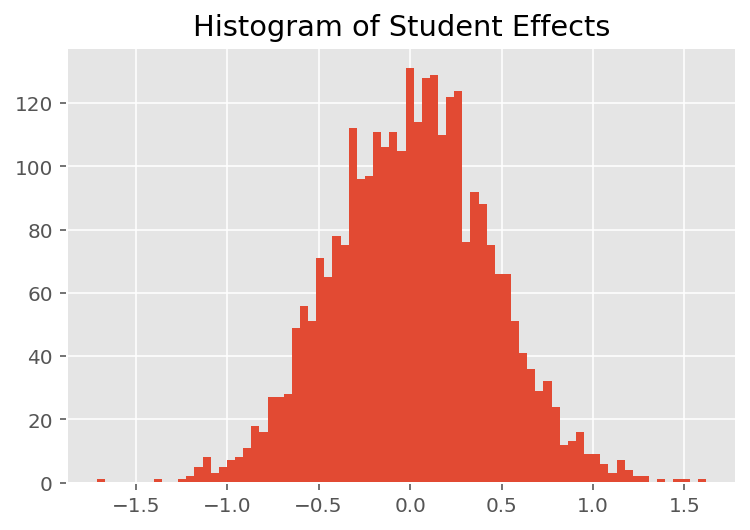
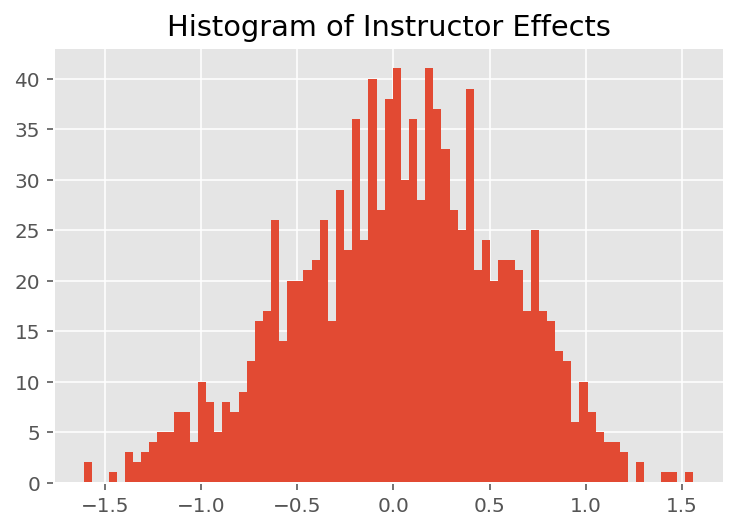
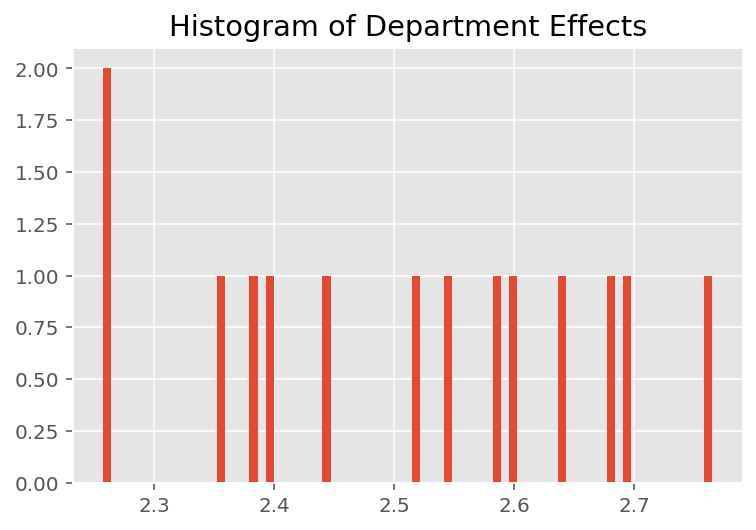
כדי לחקור כיצד המודל עושה תחזיות אינדיבידואליות, אנו מסתכלים על ההיסטוגרמה של אפקטים עבור תלמידים, מדריכים ומחלקות. זה מאפשר לנו להבין כיצד אלמנטים בודדים בוקטור תכונה של נקודת נתונים נוטים להשפיע על התוצאה.

באופן לא מפתיע, אנו רואים להלן שלכל תלמיד יש בדרך כלל השפעה מועטה על דירוג ההערכה של המורה. באופן מעניין, אנו רואים שלמחלקה אליה משתייך יש השפעה גדולה.

plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()

plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()

plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()

הערות שוליים

¹ מודלים של אפקט מעורב ליניארי הם מקרה מיוחד שבו אנו יכולים לחשב אנליטית את הצפיפות השולית שלו. למטרות מדריך זה, אנו מדגים את Monte Carlo EM, אשר חל ביתר קלות על צפיפויות שוליות לא אנליטיות, כגון אם הסבירות הייתה מורחבת להיות קטגורית במקום רגילה.

² למען הפשטות, אנו יוצרים את ממוצע ההתפלגות החזוי באמצעות מעבר אחד קדימה של המודל בלבד. זה נעשה על ידי התניה על הממוצע האחורי והוא תקף עבור מודלים של אפקטים מעורבים ליניאריים. עם זאת, זה לא תקף באופן כללי: הממוצע של ההתפלגות החזויה האחורית הוא בדרך כלל בלתי נסבל ודורש לקיחת הממוצע האמפירי על פני מספר מעברים קדימה של המודל בהינתן דגימות אחוריות.

תודות

הדרכה זו נכתבה במקור אדוארד 1.0 ( מקור ). אנו מודים לכל התורמים לכתיבת הגרסה הזו ולתיקון שלה.

הפניות

1. דאגלס בייטס ומרטין מאכלר ובן בולקר וסטיב ווקר. התאמת דגמים ליניאריים עם אפקטים מעורבים באמצעות lme4. Journal of Software הסטטיסטי, 67 (1): 1-48, 2015.

2. ארתור פ. דמפסטר, נאן מ. ליירד ודונלד ב. רובין. סבירות מרבית מנתונים לא שלמים באמצעות אלגוריתם EM. כתב העת של האגודה המלכותית סטטיסטי, סדרה B (מתודולוגיים), 1-38, 1977.

3. אנדרו גלמן וג'ניפר היל. ניתוח נתונים באמצעות רגרסיה ומודלים רב רמות/היררכיים. הוצאת אוניברסיטת קיימברידג', 2006.

4. דיוויד א. הארוויל. גישות סבירות מרבית להערכת רכיבי השונות ולבעיות קשורות. כתב העת של האגודה האמריקאית סטטיסטיים, 72 (358): 320-338, 1977.

5. מייקל אי. ג'ורדן. מבוא למודלים גרפיים. דוח טכני, 2003.

6. נאן מ. ליירד וג'יימס וור. מודלים של אפקטים אקראיים לנתונים אורכיים. ביומטריה, 963-974, 1982.

7. גרג ווי ומרטין א. טאנר. יישום מונטה קרלו של אלגוריתם EM ואלגוריתמים להגדלת הנתונים של האדם העני. כתב העת של האגודה האמריקאית סטטיסטיים, 699-704, 1990.