 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
একটি রৈখিক মিশ্র প্রভাব মডেল কাঠামোগত রৈখিক সম্পর্কের মডেলিংয়ের জন্য একটি সহজ পদ্ধতি (হারভিল, 1997; লেয়ার্ড এবং ওয়ার, 1982)। প্রতিটি ডেটা পয়েন্টে বিভিন্ন ধরনের ইনপুট থাকে—গ্রুপে শ্রেণীবদ্ধ—এবং একটি বাস্তব-মূল্যবান আউটপুট। একটি রৈখিক মিশ্র প্রভাব মডেল একটি হায়ারারকিকাল মডেল: এটি কোনো ব্যক্তি ডাটা পয়েন্ট সম্পর্কে মতামতে উপনীত উন্নত করার অংশীদারি গ্রুপ জুড়ে পরিসংখ্যানগত শক্তি।
এই টিউটোরিয়ালে, আমরা TensorFlow সম্ভাব্যতার একটি বাস্তব-বিশ্বের উদাহরণ সহ রৈখিক মিশ্র প্রভাব মডেল প্রদর্শন করি। আমরা JointDistributionCoroutine এবং মার্কভ চেইন মন্টে কার্লো (ব্যবহার করব tfp.mcmc ) মডিউল।
নির্ভরতা এবং পূর্বশর্ত
আমদানি এবং সেট আপ
import csv
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
dtype = tf.float64
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.style.use('ggplot')
জিনিস দ্রুত করুন!
আমরা ডুব দেওয়ার আগে, আসুন নিশ্চিত করি যে আমরা এই ডেমোর জন্য একটি GPU ব্যবহার করছি৷
এটি করতে, "রানটাইম" -> "রানটাইম টাইপ পরিবর্তন করুন" -> "হার্ডওয়্যার অ্যাক্সিলারেটর" -> "GPU" নির্বাচন করুন।
নিচের স্নিপেটটি যাচাই করবে যে আমাদের কাছে একটি GPU অ্যাক্সেস আছে।
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
SUCCESS: Found GPU: /device:GPU:0
ডেটা
আমরা ব্যবহার InstEval তথ্য জনপ্রিয় থেকে সেট lme4 আর প্যাকেজ (বেটস এট আল।, 2015)। এটি কোর্সের একটি ডেটা সেট এবং তাদের মূল্যায়ন রেটিং। প্রতিটি কোর্সের যেমন মেটাডেটা অন্তর্ভুক্ত students , instructors , এবং departments , এবং সুদের প্রতিক্রিয়া পরিবর্তনশীল মূল্যায়ন রেটিং।
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
আমরা ডেটা সেট লোড এবং প্রিপ্রসেস করি। আমরা 20% ডেটা ধরে রাখি যাতে আমরা অদেখা ডেটা পয়েন্টগুলিতে আমাদের লাগানো মডেলের মূল্যায়ন করতে পারি। নীচে আমরা প্রথম কয়েকটি সারি কল্পনা করি।
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
আমরা একটি পদ ডেটা সেট সেট আপ features ইনপুট অভিধানে এবং একটি labels আউটপুট রেটিং সংশ্লিষ্ট। প্রতিটি বৈশিষ্ট্য একটি পূর্ণসংখ্যা হিসাবে এনকোড করা হয় এবং প্রতিটি লেবেল (মূল্যায়ন রেটিং) একটি ফ্লোটিং পয়েন্ট সংখ্যা হিসাবে এনকোড করা হয়।
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
মডেল
একটি সাধারণ রৈখিক মডেল স্বাধীনতা ধরে নেয়, যেখানে ডেটা পয়েন্টের যেকোনো জোড়ার একটি ধ্রুবক রৈখিক সম্পর্ক থাকে। ইন InstEval ডেটা সেট, পর্যবেক্ষণ গ্রুপ প্রতিটি যা তারতম্য ঢালে এবং বিবৃতি থাকতে পারে মধ্যে উঠা। রৈখিক মিশ্র প্রভাব মডেল, এছাড়াও ক্রমানুসারী রৈখিক মডেল বা বহুস্তরীয় রৈখিক মডেল হিসাবে পরিচিত, এই ঘটনাটি ক্যাপচার (Gelman & Hill, 2006)।
এই ঘটনার উদাহরণগুলির মধ্যে রয়েছে:
- শিক্ষার্থীরা। একজন শিক্ষার্থীর পর্যবেক্ষণ স্বাধীন নয়: কিছু শিক্ষার্থী পদ্ধতিগতভাবে কম (বা উচ্চ) লেকচার রেটিং দিতে পারে।
- প্রশিক্ষক। একজন প্রশিক্ষকের কাছ থেকে পর্যবেক্ষণ স্বাধীন নয়: আমরা আশা করি ভালো শিক্ষকদের সাধারণত ভালো রেটিং থাকবে এবং খারাপ শিক্ষকদের সাধারণত খারাপ রেটিং থাকবে।
- বিভাগ। একটি বিভাগ থেকে পর্যবেক্ষণ স্বাধীন নয়: নির্দিষ্ট বিভাগের সাধারণত শুষ্ক উপাদান বা কঠোর গ্রেডিং থাকতে পারে এবং এইভাবে অন্যদের তুলনায় কম রেট করা যেতে পারে।
এই, রিকল একটি ডেটা সেট যে ক্যাপচার করার জন্য \(N\times D\) অতিরিক্ত বৈশিষ্ট্যগুলিও উপস্থিত রয়েছে \(\mathbf{X}\) এবং \(N\) লেবেল \(\mathbf{y}\), রৈখিক নির্ভরণ posits মডেল
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
যেখানে একটি ঢাল ভেক্টর আছে \(\beta\in\mathbb{R}^D\), পথিমধ্যে \(\alpha\in\mathbb{R}\)এবং রান্ডম নয়েজ \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)। আমরা যে \(\beta\) এবং \(\alpha\) "fixed প্রভাব" হয়: তারা ডাটা পয়েন্টের জনসংখ্যা জুড়ে অনুষ্ঠিত ধ্রুবক প্রভাব \((x, y)\)। একটি সম্ভাবনা যেমন সমীকরণের একটি সমতুল্য তৈয়ার হয় \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\)। এই সম্ভাবনা আদেশের বিন্দু অনুমান এটি করার জন্য অনুমান সময় বড় করা হয় \(\beta\) এবং \(\alpha\) যে ডেটা মাপসই করা হবে।
একটি রৈখিক মিশ্র প্রভাব মডেল হিসাবে রৈখিক রিগ্রেশন প্রসারিত
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
যেখানে এখনও একটি ঢাল ভেক্টর হয় \(\beta\in\mathbb{R}^P\), পথিমধ্যে \(\alpha\in\mathbb{R}\)এবং রান্ডম নয়েজ \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)। উপরন্তু, একটি শব্দ \(\mathbf{Z}\eta\), যেখানে \(\mathbf{Z}\) একটি বৈশিষ্ট্য ম্যাট্রিক্স এবং \(\eta\in\mathbb{R}^Q\) র্যান্ডম ঢালে একটি ভেক্টর হয়; \(\eta\) স্বাভাবিকভাবে ভ্যারিয়েন্স উপাদান পরামিতি সঙ্গে বিতরণ করা হয় \(\sigma^2\)। \(\mathbf{Z}\) মূল পার্টিশন প্রক্রিয়ার দ্বারা গঠিত হয় \(N\times D\) একটি নতুন পদ ম্যাট্রিক্স অতিরিক্ত বৈশিষ্ট্যগুলিও উপস্থিত রয়েছে \(N\times P\) ম্যাট্রিক্স \(\mathbf{X}\) এবং \(N\times Q\) ম্যাট্রিক্স \(\mathbf{Z}\), যেখানে \(P + Q=D\)এই পার্টিশন আমাদের ব্যবহার করে পৃথকভাবে বৈশিষ্ট্য মডেল অনুমতি দেয়: সংশোধন করা হয়েছে প্রভাব \(\beta\) এবং প্রচ্ছন্ন পরিবর্তনশীল \(\eta\) যথাক্রমে।
বলতে সুপ্ত ভেরিয়েবল \(\eta\) "র্যান্ডম প্রভাব" হয়: তারা প্রভাব জনসংখ্যা জুড়ে পরিবর্তিত হতে (যদিও তারা subpopulations জুড়ে ধ্রুবক হতে পারে) আছে। বিশেষ করে, কারণ র্যান্ডম প্রভাব \(\eta\) গড় 0 ডেটা লেবেল এর গড় ক্যাপচার হয়, \(\mathbf{X}\beta + \alpha\)। র্যান্ডম প্রভাব উপাদান \(\mathbf{Z}\eta\) তথ্য যেমনটি বৈচিত্র: "। প্রশিক্ষক # 54 1.4 পয়েন্ট গড় চাইতে বেশী রেট হয়" উদাহরণস্বরূপ,
এই টিউটোরিয়ালে, আমরা নিম্নলিখিত প্রভাবগুলি রাখি:
- ফিক্সড এফেক্টস:
service।serviceএকটি বাইনারি কোর্সের প্রশিক্ষক প্রধান ডিপার্টমেন্টে কিনা তা সংশ্লিষ্ট covariate হয়। কোন ব্যাপার আমরা কতটা অতিরিক্ত তথ্য সংগ্রহের, এটি শুধুমাত্র মান নিতে পারেন \(0\) এবং \(1\)। - এলোমেলো এফেক্টস:
students,instructors, এবংdepartments। কোর্স মূল্যায়ন রেটিং জনসংখ্যা থেকে আরো পর্যবেক্ষণ দেওয়া, আমরা নতুন ছাত্র, শিক্ষক, বা বিভাগ খুঁজছি হতে পারে.
R-এর lme4 প্যাকেজের সিনট্যাক্সে (Bates et al., 2015), মডেলটিকে সংক্ষিপ্ত করা যেতে পারে
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
যেখানে x উল্লেখ করে একটি নির্দিষ্ট প্রভাব, (1|x) জন্য একটি র্যান্ডম প্রভাব উল্লেখ করে x , এবং 1 একটি পথিমধ্যে মেয়াদ উল্লেখ করে।
আমরা নিচের এই মডেলটিকে জয়েন্ট ডিস্ট্রিবিউশন হিসেবে বাস্তবায়ন করি। পরামিতি ট্র্যাকিং জন্য ভাল সমর্থন আছে (যেমন, আমরা সব ট্র্যাক করতে চান tf.Variable মধ্যে model.trainable_variables , আমরা যেমন মডেল টেমপ্লেট বাস্তবায়ন) tf.Module ।
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=self._stddev_students),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=self._stddev_instructors),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_identity_multiplier=self._stddev_departments),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>)
একটি সম্ভাব্য গ্রাফিকাল প্রোগ্রাম হিসাবে, আমরা এর গণনামূলক গ্রাফের পরিপ্রেক্ষিতে মডেলের কাঠামোটি কল্পনা করতে পারি। এই গ্রাফটি প্রোগ্রামের র্যান্ডম ভেরিয়েবল জুড়ে ডেটাফ্লোকে এনকোড করে, একটি গ্রাফিকাল মডেলের পরিপ্রেক্ষিতে তাদের সম্পর্ককে স্পষ্ট করে তোলে (জর্ডান, 2003)।
একটি পরিসংখ্যানগত টুল হিসাবে, আমরা গ্রাফ এ অনুক্রমে আরও ভালোভাবে দেখতে, উদাহরণস্বরূপ চেহারা হতে পারে, যে intercept এবং effect_service শর্তসাপেক্ষে নির্ভরশীল দেওয়া হয় ratings ; প্রোগ্রামটি ক্লাস, মডিউল জুড়ে ক্রস রেফারেন্স, এবং/অথবা সাবরুটিন দিয়ে লেখা হলে সোর্স কোড থেকে এটি দেখা কঠিন হতে পারে। একটি গণনীয় হাতিয়ার হিসেবে, আমরা সুপ্ত ভেরিয়েবল মধ্যে প্রবাহিত লক্ষ্য পারে ratings মাধ্যমে পরিবর্তনশীল tf.gather অপস। এই নির্দিষ্ট হার্ডওয়্যার ত্বরক একটি বোতলের হতে পারে যদি ইন্ডেক্স Tensor গুলি ব্যয়বহুল; গ্রাফটি ভিজ্যুয়ালাইজ করা এটিকে সহজেই স্পষ্ট করে তোলে।
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
পরামিতি অনুমান
তথ্য দেওয়া, অনুমান লক্ষ্য মডেলের সংশোধন প্রভাব ঢাল মাপসই হয় \(\beta\), পথিমধ্যে \(\alpha\)এবং ভ্যারিয়েন্স উপাদান প্যারামিটার \(\sigma^2\)। সর্বাধিক সম্ভাবনা নীতি হিসাবে এই কাজ formalizes
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
এই টিউটোরিয়ালে, আমরা এই প্রান্তিক ঘনত্বকে সর্বাধিক করার জন্য মন্টে কার্লো ইএম অ্যালগরিদম ব্যবহার করি (ডেম্পস্টার এট আল।, 1977; ওয়েই এবং ট্যানার, 1990)।¹ আমরা শর্তসাপেক্ষ সম্ভাবনার প্রত্যাশা গণনা করতে মার্কভ চেইন মন্টে কার্লো সম্পাদন করি। এলোমেলো প্রভাব ("ই-পদক্ষেপ"), এবং আমরা প্যারামিটার ("M-পদক্ষেপ") এর ক্ষেত্রে প্রত্যাশা সর্বাধিক করার জন্য গ্রেডিয়েন্ট ডিসেন্ট সঞ্চালন করি:
ই-পদক্ষেপের জন্য, আমরা হ্যামিলটোনিয়ান মন্টে কার্লো (HMC) সেট আপ করি। এটি একটি বর্তমান অবস্থা নেয়—ছাত্র, প্রশিক্ষক এবং বিভাগের প্রভাব—এবং একটি নতুন অবস্থা ফিরিয়ে দেয়। আমরা TensorFlow ভেরিয়েবলে নতুন স্টেট বরাদ্দ করি, যা HMC চেইনের অবস্থা নির্দেশ করবে।
এম-পদক্ষেপের জন্য, আমরা একটি ধ্রুবক পর্যন্ত প্রান্তিক সম্ভাবনার একটি নিরপেক্ষ অনুমান গণনা করতে HMC থেকে উত্তরের নমুনা ব্যবহার করি। তারপরে আমরা আগ্রহের প্যারামিটারের সাথে এর গ্রেডিয়েন্ট প্রয়োগ করি। এটি প্রান্তিক সম্ভাবনার উপর একটি নিরপেক্ষ স্টোকাস্টিক ডিসেন্ট স্টেপ তৈরি করে। আমরা এটিকে অ্যাডাম টেনসরফ্লো অপ্টিমাইজার দিয়ে বাস্তবায়ন করি এবং প্রান্তিকের নেতিবাচককে কমিয়ে দেই।
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-528062.5>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
আমরা একটি ওয়ার্ম-আপ স্টেজ সঞ্চালন করি, যা একাধিক পুনরাবৃত্তির জন্য একটি MCMC চেইন চালায় যাতে প্রশিক্ষণটি পোস্টেরিয়র সম্ভাব্যতা ভরের মধ্যে শুরু করা যেতে পারে। আমরা তারপর একটি প্রশিক্ষণ লুপ চালানো. এটি যৌথভাবে E এবং M-পদক্ষেপ চালায় এবং প্রশিক্ষণের সময় মান রেকর্ড করে।
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.754 Warm-Up Iteration: 999 Acceptance Rate: 0.707 Iteration: 0 Acceptance Rate: 1.000 Loss: 98220.266 Iteration: 500 Acceptance Rate: 0.703 Loss: 96003.969 Iteration: 1000 Acceptance Rate: 0.678 Loss: 95958.609 Iteration: 1499 Acceptance Rate: 0.685 Loss: 95921.891
এছাড়াও আপনি একটি মধ্যে জন্য-লুপ warmup লিখতে পারেন tf.while_loop , এবং একটি মধ্যে প্রশিক্ষণ পদক্ষেপ tf.scan বা tf.while_loop আরও দ্রুত অনুমান জন্য। উদাহরণ স্বরূপ:
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
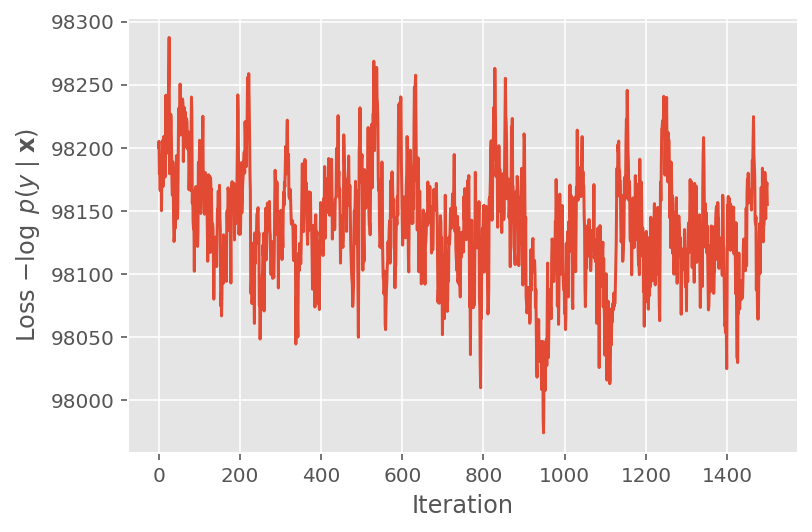
উপরে, একটি কনভারজেন্স থ্রেশহোল্ড সনাক্ত না হওয়া পর্যন্ত আমরা অ্যালগরিদম চালাইনি। প্রশিক্ষণ বুদ্ধিমান ছিল কিনা তা পরীক্ষা করার জন্য, আমরা যাচাই করি যে ক্ষতির কার্যকারিতা প্রকৃতপক্ষে প্রশিক্ষণের পুনরাবৃত্তির উপর একত্রিত হয়।
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
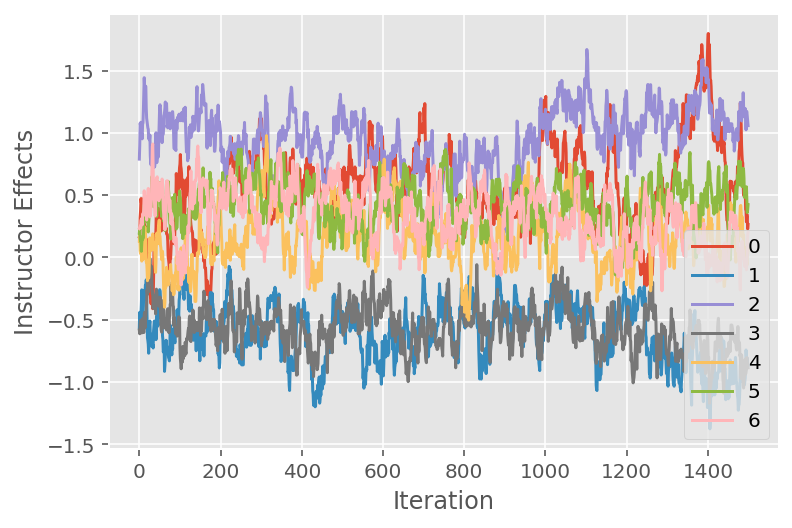
আমরা একটি ট্রেস প্লটও ব্যবহার করি, যা নির্দিষ্ট সুপ্ত মাত্রা জুড়ে মার্কভ চেইন মন্টে কার্লো অ্যালগরিদমের গতিপথ দেখায়। নীচে আমরা দেখতে পাই যে নির্দিষ্ট প্রশিক্ষকের প্রভাবগুলি প্রকৃতপক্ষে অর্থপূর্ণভাবে তাদের প্রাথমিক অবস্থা থেকে দূরে সরে যায় এবং রাজ্যের স্থানটি অন্বেষণ করে। ট্রেস প্লটটি ইঙ্গিত করে যে প্রভাবগুলি প্রশিক্ষকদের মধ্যে ভিন্ন কিন্তু একই ধরনের মিশ্রণ আচরণের সাথে।
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
সমালোচনা
উপরে, আমরা মডেল লাগানো. আমরা এখন ডেটা ব্যবহার করে এর উপযুক্ত সমালোচনা করার দিকে নজর দিই, যা আমাদেরকে মডেলটি অন্বেষণ করতে এবং আরও ভালভাবে বুঝতে দেয়। এই ধরনের একটি কৌশল হল একটি অবশিষ্ট প্লট, যা প্রতিটি ডেটা পয়েন্টের জন্য মডেলের ভবিষ্যদ্বাণী এবং স্থল সত্যের মধ্যে পার্থক্য তৈরি করে। যদি মডেলটি সঠিক ছিল, তাহলে তাদের পার্থক্যটি সাধারণভাবে বিতরণ করা উচিত; প্লটে এই প্যাটার্ন থেকে কোনো বিচ্যুতি মডেলের অসঙ্গতি নির্দেশ করে।
আমরা প্রথমে রেটিং ওভার পোস্টেরিয়র প্রেডিকটিভ ডিস্ট্রিবিউশন গঠন করে অবশিষ্ট প্লট তৈরি করি, যা র্যান্ডম ইফেক্টের পূর্বের ডিস্ট্রিবিউশনকে তার উত্তর প্রদত্ত প্রশিক্ষণ ডেটা দিয়ে প্রতিস্থাপন করে। বিশেষ করে, আমরা মডেলটিকে সামনের দিকে চালাই এবং পূর্বের র্যান্ডম প্রভাবের উপর নির্ভরতাকে তাদের অনুমানকৃত পোস্টেরিয়র উপায়ে আটকাই।²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
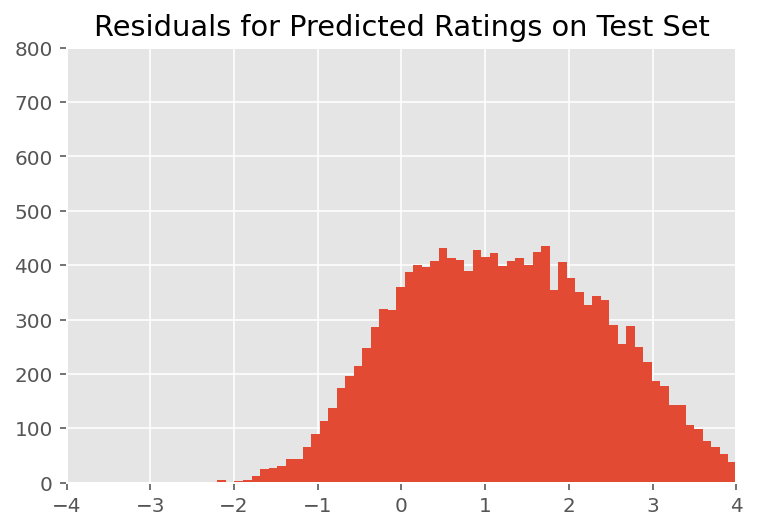
চাক্ষুষ পরিদর্শন করার পরে, অবশিষ্টাংশগুলিকে কিছুটা মানক-সাধারণত বিতরণ করা দেখায়। যাইহোক, ফিটটি নিখুঁত নয়: একটি স্বাভাবিক বন্টনের তুলনায় লেজের মধ্যে বৃহত্তর সম্ভাবনার ভর রয়েছে, যা নির্দেশ করে যে মডেলটি তার স্বাভাবিকতা অনুমানগুলি শিথিল করে তার ফিট উন্নত করতে পারে।
বিশেষ করে, যদিও এটি সবচেয়ে মডেল রেটিং একটি স্বাভাবিক বন্টন ব্যবহার করতে হবে সাধারণ InstEval ডেটা সেট, ডাটা এ পুরো বিষয়টা বিস্তারিত বিবেচনা জানায় যে কোর্স মূল্যায়ন রেটিং এর মানে দাড়ায় যে আমরা ব্যবহার করা উচিত 1 থেকে 5 আসলে পূরণবাচক মান হয় একটি অর্ডিনাল ডিস্ট্রিবিউশন, বা এমনকি ক্যাটেগরিকাল যদি আমাদের কাছে আপেক্ষিক ক্রমটি ফেলে দেওয়ার জন্য যথেষ্ট ডেটা থাকে। এটি উপরের মডেলে একটি এক-লাইন পরিবর্তন; একই অনুমান কোড প্রযোজ্য।
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
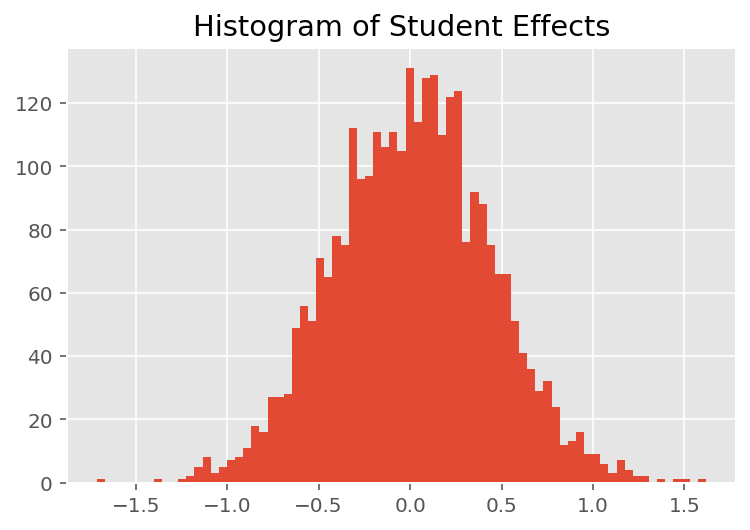
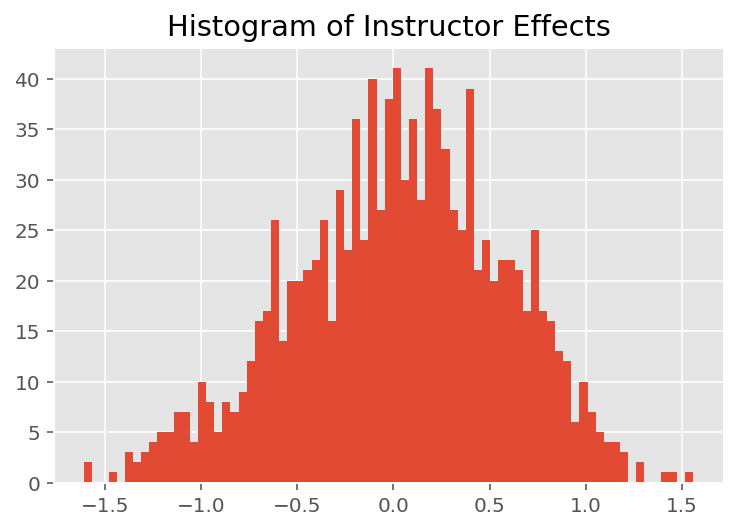
মডেলটি কীভাবে পৃথক ভবিষ্যদ্বাণী করে তা অন্বেষণ করতে, আমরা ছাত্র, প্রশিক্ষক এবং বিভাগের জন্য প্রভাবের হিস্টোগ্রাম দেখি। এটি আমাদের বুঝতে দেয় যে কীভাবে ডেটা পয়েন্টের বৈশিষ্ট্য ভেক্টরের পৃথক উপাদানগুলি ফলাফলকে প্রভাবিত করে।
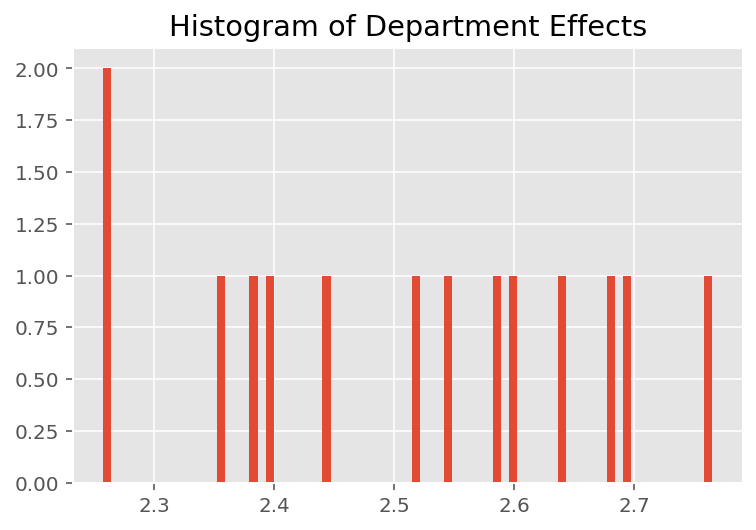
আশ্চর্যের বিষয় নয়, আমরা নীচে দেখতে পাচ্ছি যে প্রতিটি শিক্ষার্থী সাধারণত একজন প্রশিক্ষকের মূল্যায়ন রেটিংয়ে সামান্য প্রভাব ফেলে। মজার বিষয় হল, আমরা দেখতে পাই যে একজন প্রশিক্ষক যে বিভাগের অন্তর্গত তার একটি বড় প্রভাব রয়েছে।
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
পাদটীকা
¹ লিনিয়ার মিশ্র প্রভাব মডেল একটি বিশেষ ক্ষেত্রে যেখানে আমরা বিশ্লেষণাত্মকভাবে এর প্রান্তিক ঘনত্ব গণনা করতে পারি। এই টিউটোরিয়ালের উদ্দেশ্যে, আমরা মন্টে কার্লো EM প্রদর্শন করি, যা আরও সহজে অ-বিশ্লেষক প্রান্তিক ঘনত্বের ক্ষেত্রে প্রযোজ্য যেমন যদি সম্ভাবনাটি সাধারণের পরিবর্তে শ্রেণীবদ্ধ হওয়ার সম্ভাবনা বাড়ানো হয়।
² সরলতার জন্য, আমরা মডেলের শুধুমাত্র একটি ফরোয়ার্ড পাস ব্যবহার করে ভবিষ্যদ্বাণীমূলক বিতরণের গড় তৈরি করি। এটি পোস্টেরিয়র গড় উপর কন্ডিশনার দ্বারা করা হয় এবং লিনিয়ার মিশ্র প্রভাব মডেলের জন্য বৈধ। যাইহোক, এটি সাধারণভাবে বৈধ নয়: পোস্টেরিয়র ভবিষ্যদ্বাণীমূলক ডিস্ট্রিবিউশনের গড় সাধারণত জটিল হয় এবং প্রদত্ত মডেলের পোস্টেরিয়র নমুনাগুলির একাধিক ফরোয়ার্ড পাস জুড়ে অভিজ্ঞতামূলক গড় নেওয়া প্রয়োজন।
স্বীকৃতি
এই টিউটোরিয়ালটি মূলত এডওয়ার্ড 1.0 (লেখা ছিল উৎস )। আমরা সেই সংস্করণটি লেখা এবং সংশোধন করার জন্য সমস্ত অবদানকারীদের ধন্যবাদ জানাই।
তথ্যসূত্র
ডগলাস বেটস এবং মার্টিন মাখলার এবং বেন বলকার এবং স্টিভ ওয়াকার। lme4 ব্যবহার করে ফিটিং লিনিয়ার মিক্সড-ইফেক্ট মডেল। পরিসংখ্যানগত সফটওয়্যার 67 জার্নাল (1): 1-48, 2015।
আর্থার পি. ডেম্পস্টার, ন্যান এম লেয়ার্ড এবং ডোনাল্ড বি রুবিন। EM অ্যালগরিদমের মাধ্যমে অসম্পূর্ণ ডেটা থেকে সর্বাধিক সম্ভাবনা। রয়েল পরিসংখ্যানগত সোসাইটির জার্নাল, সিরিজ বি (পদ্ধতিগত), 1-38, 1977।
অ্যান্ড্রু গেলম্যান এবং জেনিফার হিল। রিগ্রেশন এবং মাল্টিলেভেল/শ্রেণিক্রমিক মডেল ব্যবহার করে ডেটা বিশ্লেষণ। কেমব্রিজ ইউনিভার্সিটি প্রেস, 2006।
ডেভিড এ হারভিল। বৈকল্পিক উপাদান অনুমান এবং সম্পর্কিত সমস্যাগুলির জন্য সর্বাধিক সম্ভাবনার পন্থা। আমেরিকান পরিসংখ্যানগত অ্যাসোসিয়েশনের জার্নাল, 72 (358): 320-338, 1977।
মাইকেল আই জর্ডান। গ্রাফিক্যাল মডেলের একটি ভূমিকা। প্রযুক্তিগত প্রতিবেদন, 2003।
ন্যান এম লেয়ার্ড এবং জেমস ওয়ার। অনুদৈর্ঘ্য ডেটার জন্য র্যান্ডম-প্রভাব মডেল। বায়োমেট্রিক্স, 963-974, 1982।
গ্রেগ ওয়েই এবং মার্টিন এ ট্যানার। একটি মন্টে কার্লো ইএম অ্যালগরিদম এবং দরিদ্র মানুষের ডেটা অগমেন্টেশন অ্যালগরিদমের বাস্তবায়ন। আমেরিকান পরিসংখ্যানগত অ্যাসোসিয়েশনের জার্নাল, 699-704, 1990।
