 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Cài đặt
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
Cài đặt
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
trừu tượng
Trong chuyên mục này, chúng tôi trình bày cách điều chỉnh mô hình hiệu ứng hỗn hợp tuyến tính tổng quát bằng cách sử dụng suy luận biến thiên trong Xác suất TensorFlow.
Gia đình kiểu mẫu
Khái quát hóa tuyến tính mô hình hỗn hợp hiệu lực thi hành (GLMM) cũng tương tự như khái quát hóa tuyến tính mô hình (GLM) ngoại trừ việc họ kết hợp một tiếng ồn mẫu cụ thể vào các phản ứng tuyến tính dự đoán. Điều này hữu ích một phần vì nó cho phép các tính năng hiếm thấy chia sẻ thông tin với các tính năng thường thấy hơn.
Là một quá trình tổng quát, Mô hình hiệu ứng hỗn hợp tuyến tính tổng quát (GLMM) được đặc trưng bởi:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
ở đâu:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
Nói cách khác, điều này nói rằng tất cả các chủng loại mỗi nhóm được kết hợp với một mẫu, \(\beta_{rc}\), từ một bình thường đa biến. Mặc dù \(\beta_{rc}\) rút luôn độc lập, họ chỉ indentically phân phối cho một nhóm \(r\): Thông báo có đúng một \(\Sigma_r\) cho mỗi \(r\in\{1,\ldots,R\}\).
Khi affinely kết hợp với các tính năng nhóm của một mẫu (\(z_{r,i}\)), kết quả là mẫu cụ thể tiếng ồn trên \(i\)-thứ dự đoán phản ứng tuyến tính (đó là trường hợp \(x_i^\top\omega\)).
Khi chúng tôi ước tính \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) chúng ta đang chủ yếu ước lượng nhiễu một nhóm ngẫu nhiên hiệu ứng mang mà nếu không sẽ bị chết đuối ra hiện tín hiệu trong \(x_i^\top\omega\).
Có một loạt các tùy chọn cho \(\text{Distribution}\) và chức năng liên kết ngược , \(g^{-1}\). Các lựa chọn phổ biến là:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), và,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
Đối với khả năng hơn, hãy xem các tfp.glm module.
Suy luận biến đổi
Thật không may, việc tìm kiếm ước tính khả năng tối đa của các thông số \(\beta,\{\Sigma_r\}_r^R\) đòi hỏi một thể thiếu không phân tích. Để giải quyết vấn đề này, chúng tôi thay vào đó
- Định nghĩa một gia đình tham số của phân phối (các "người thay thế mật độ"), ký hiệu là \(q_{\lambda}\) trong phụ lục.
- Tìm thông số \(\lambda\) để \(q_{\lambda}\) gần denstiy mục tiêu thật sự của mình.
Gia đình của các bản phân phối sẽ Gaussian phụ thuộc vào kích thước thích hợp, và bởi "gần mật độ mục tiêu của chúng tôi", chúng tôi sẽ có nghĩa là "giảm thiểu sự phân kỳ Kullback-Leibler ". Xem, ví dụ mục 2.2 của "Variational Suy luận: Một đánh giá cho nhà thống kê" cho một derivation tốt bằng văn bản và động lực. Đặc biệt, nó cho thấy rằng việc giảm thiểu sự phân kỳ KL tương đương với việc giảm thiểu giới hạn dưới bằng chứng phủ định (ELBO).
Vấn đề đồ chơi
Gelman et al. (2007) "dataset radon" là một tập dữ liệu đôi khi được dùng để chứng minh phương pháp tiếp cận đối với hồi quy. (Ví dụ, có liên quan chặt chẽ này bài PyMC3 viết blog .) Bộ dữ liệu radon chứa các phép đo trong nhà của Radon lấy trên khắp Hoa Kỳ. Radon là một cách tự nhiên ocurring khí phóng xạ đó là độc ở nồng độ cao.
Đối với minh chứng của chúng tôi, giả sử chúng tôi quan tâm đến việc xác thực giả thuyết rằng mức Radon cao hơn trong các hộ gia đình có tầng hầm. Chúng tôi cũng nghi ngờ nồng độ Radon có liên quan đến loại đất, tức là các vấn đề địa lý.
Để định hình đây là một bài toán ML, chúng tôi sẽ cố gắng dự đoán các mức log-radon dựa trên một hàm tuyến tính của tầng mà kết quả đọc được thực hiện. Chúng tôi cũng sẽ sử dụng quận như một hiệu ứng ngẫu nhiên và làm như vậy sẽ tính đến sự khác biệt do địa lý. Nói cách khác, chúng tôi sẽ sử dụng một mô hình hỗn hợp hiệu ứng tuyến tính tổng quát .
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Chúng tôi cũng sẽ kiểm tra nhanh tính khả dụng của GPU:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
Lấy tập dữ liệu:
Chúng tôi tải tập dữ liệu từ tập dữ liệu TensorFlow và thực hiện một số xử lý trước nhẹ.
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
Chuyên môn hóa gia đình GLMM
Trong phần này, chúng tôi chuyên môn hóa họ GLMM với nhiệm vụ dự đoán mức radon. Để làm điều này, trước tiên chúng ta xem xét trường hợp đặc biệt hiệu ứng cố định của GLMM:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
Mô hình này thừa nhận rằng radon log trong quan sát \(j\) là (trong sự mong đợi) chi phối bởi Sàn \(j\)thứ đọc được lấy về, cộng với một số liên tục đánh chặn. Trong mã giả, chúng ta có thể viết
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
có một trọng lượng học kinh nghiệm cho mỗi tầng và phổ quát intercept hạn. Nhìn vào các phép đo radon từ tầng 0 và 1, có vẻ như đây có thể là một khởi đầu tốt:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
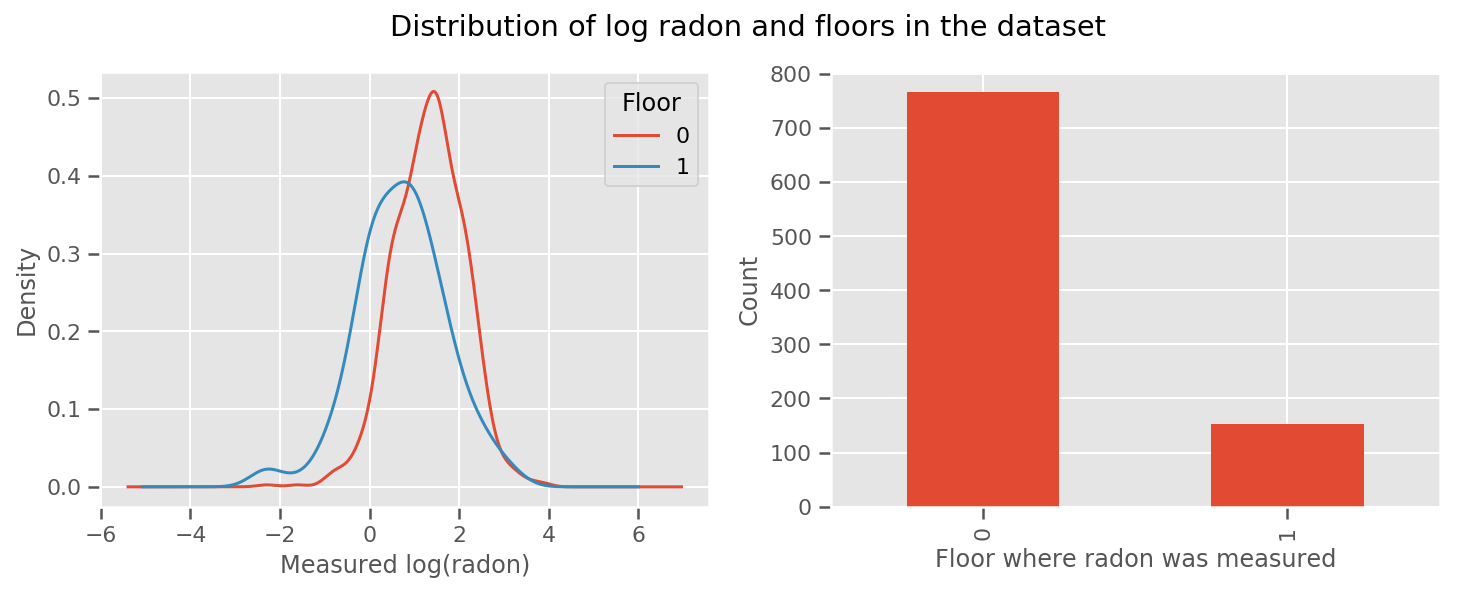
Để làm cho mô hình phức tạp hơn một chút, bao gồm một số điều về địa lý có lẽ còn tốt hơn: radon là một phần của chuỗi phân rã của uranium, có thể có trong lòng đất, vì vậy địa lý dường như là chìa khóa để giải thích.
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
Một lần nữa, trong mã giả, chúng ta có
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
giống như trước đây ngoại trừ trọng lượng cụ thể của quận.
Với một tập hợp đào tạo đủ lớn, đây là một mô hình hợp lý. Tuy nhiên, dựa trên dữ liệu của chúng tôi từ Minnesota, chúng tôi thấy rằng có một số lượng lớn các hạt với một số lượng nhỏ các phép đo. Ví dụ, 39 trong số 85 quận có ít hơn năm quan sát.
Điều này thúc đẩy chia sẻ sức mạnh thống kê giữa tất cả các quan sát của chúng tôi, theo cách hội tụ vào mô hình trên khi số lượng quan sát trên mỗi quận tăng lên.
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
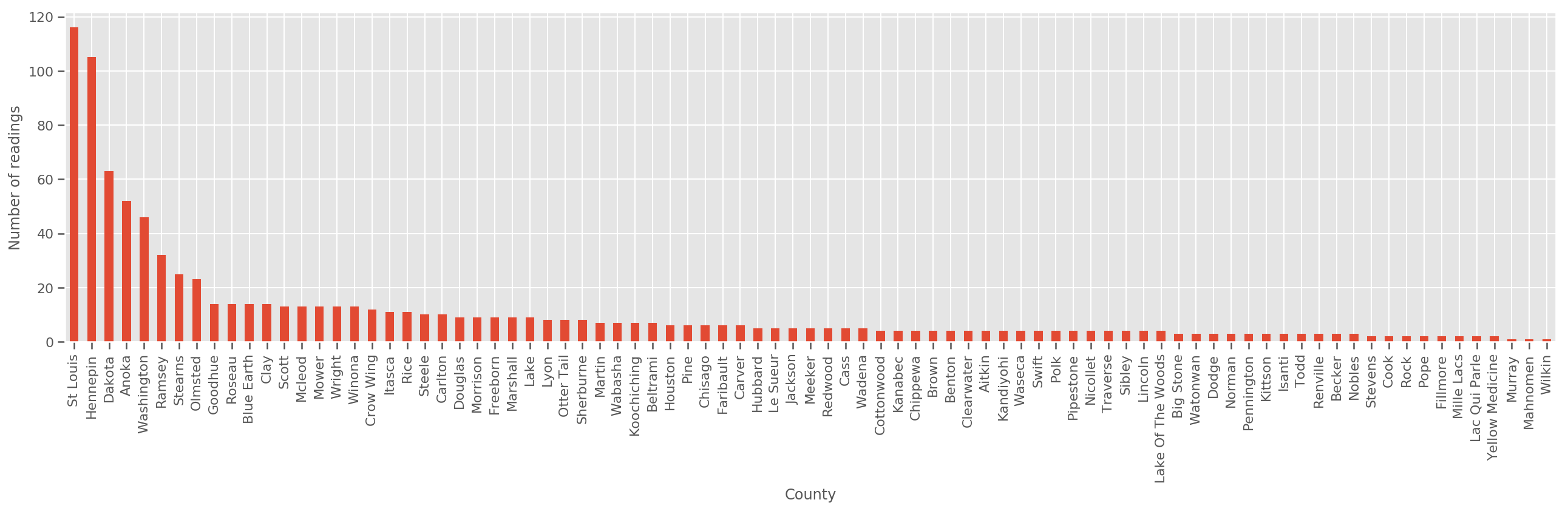
Nếu chúng ta phù hợp với mô hình này, county_effect vector có khả năng sẽ kết thúc ghi nhớ các kết quả cho các quận trong đó chỉ có một vài mẫu đào tạo, có lẽ overfitting và dẫn đến sự tổng quát nghèo.
GLMM's cung cấp một trung bình vui vẻ cho hai GLM trên. Chúng tôi có thể xem xét việc phù hợp
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
Mô hình này cũng giống như người đầu tiên, nhưng chúng tôi đã cố định khả năng của chúng tôi để trở thành một phân phối chuẩn, và sẽ chia sẻ phương sai trên tất cả các quận thông qua (duy nhất) biến county_scale . Trong mã giả,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
Chúng tôi sẽ suy ra sự phân bố doanh trên county_scale , county_mean , và random_effect sử dụng dữ liệu quan sát của chúng tôi. Toàn cầu county_scale cho phép chúng ta chia sẻ sức mạnh thống kê qua các quận: những người có nhiều quan sát cung cấp một hit tại phương sai của quận với vài quan sát. Hơn nữa, khi chúng tôi thu thập nhiều dữ liệu hơn, mô hình này sẽ hội tụ thành mô hình mà không có biến tỷ lệ tổng hợp - ngay cả với tập dữ liệu này, chúng tôi sẽ đi đến kết luận tương tự về các hạt được quan sát nhiều nhất với một trong hai mô hình.
Thí nghiệm
Bây giờ chúng tôi sẽ cố gắng điều chỉnh GLMM ở trên bằng cách sử dụng suy luận biến phân trong TensorFlow. Đầu tiên, chúng tôi sẽ chia dữ liệu thành các tính năng và nhãn.
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
Chỉ định mô hình
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
Chỉ định hậu quả đại diện
Bây giờ chúng ta đặt cùng một gia đình thay thế \(q_{\lambda}\), nơi mà các thông số \(\lambda\) là khả năng huấn luyện. Trong trường hợp này, gia đình của chúng tôi là độc lập phân phối đa biến bình thường, một cho mỗi tham số, và \(\lambda = \{(\mu_j, \sigma_j)\}\), nơi \(j\) chỉ số bốn thông số.
Phương pháp này chúng tôi sử dụng để phù hợp với gia đình thay thế sử dụng tf.Variables . Chúng tôi cũng sử dụng tfp.util.TransformedVariable cùng với Softplus để hạn chế các thông số (khả năng huấn luyện) quy mô là tích cực. Thêm vào đó, chúng tôi áp dụng Softplus cho toàn bộ scale_prior , mà là một tham số dương.
Chúng tôi khởi tạo các biến có thể huấn luyện này với một chút rung động để hỗ trợ tối ưu hóa.
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
Lưu ý rằng các tế bào này có thể được thay thế bằng tfp.experimental.vi.build_factored_surrogate_posterior , như trong:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
Các kết quả
Nhớ lại rằng mục tiêu của chúng ta là xác định một họ phân phối được tham số hóa có thể định hướng và sau đó chọn các tham số để chúng ta có một phân phối có thể định hướng gần với phân phối đích của chúng ta.
Chúng tôi đã xây dựng được phân phối thay thế ở trên, và có thể sử dụng tfp.vi.fit_surrogate_posterior , mà chấp nhận một ưu và một số lượng nhất định các bước sau để tìm các tham số cho mô hình thay thế giảm thiểu ELBO tiêu cực (mà corresonds để giảm thiểu sự phân kỳ Kullback-Liebler giữa người đại diện và phân phối đích).
Giá trị trả về là ELBO tiêu cực tại mỗi bước, và phân phối trong surrogate_posterior sẽ được cập nhật với các thông số được tìm thấy bởi tôi ưu hoa.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
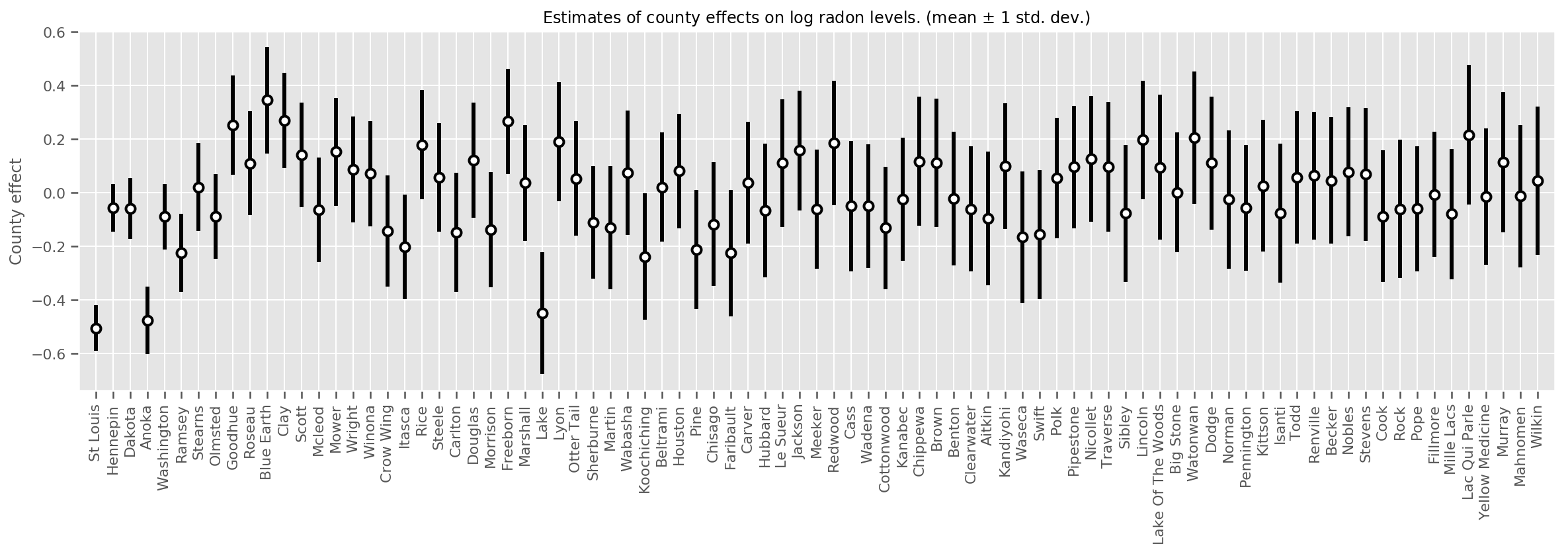
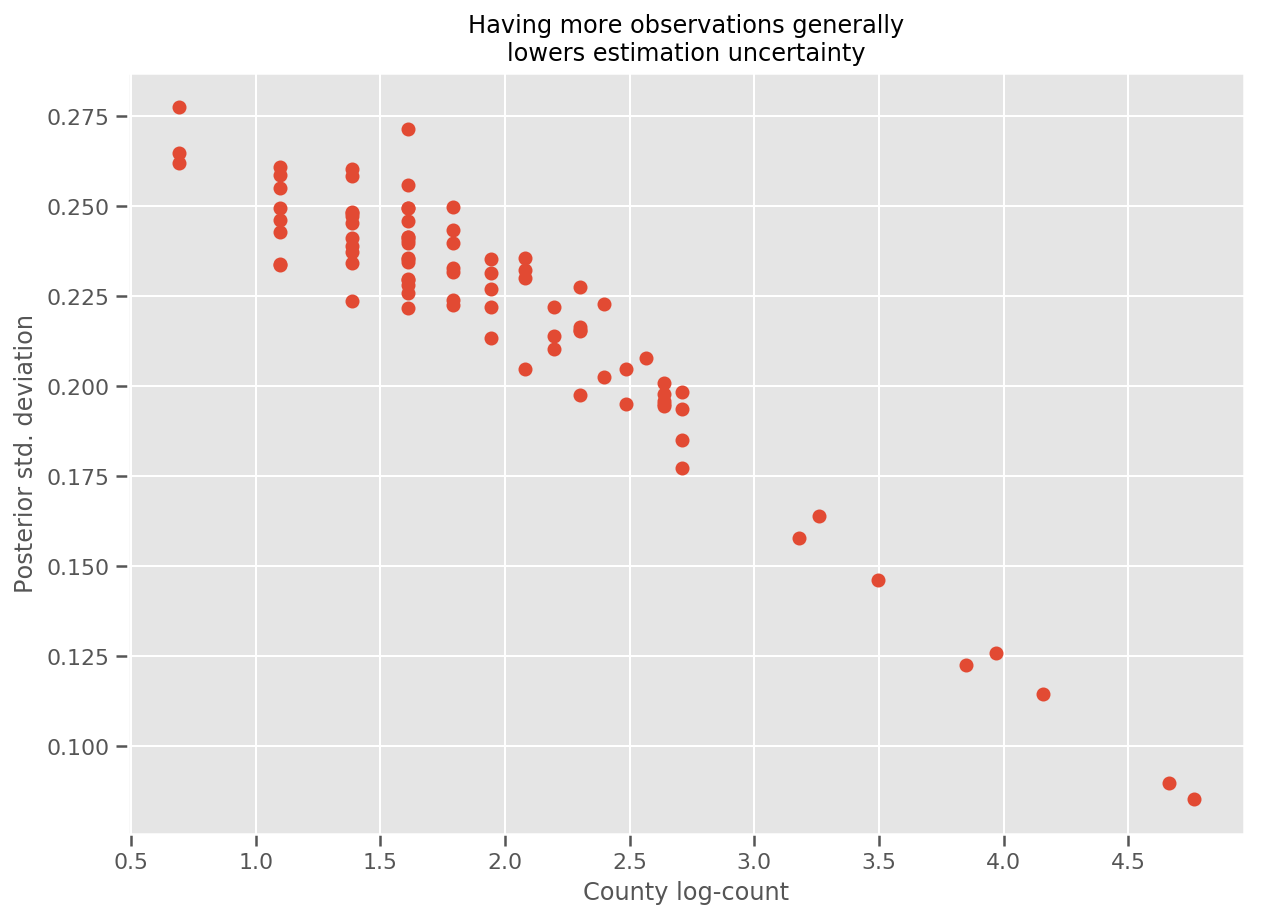
Chúng ta có thể vẽ biểu đồ các hiệu ứng hạt trung bình ước tính, cùng với độ không chắc chắn của giá trị trung bình đó. Chúng tôi đã sắp xếp thứ tự này theo số lượng quan sát, với quan sát lớn nhất ở bên trái. Lưu ý rằng độ không đảm bảo đo nhỏ đối với các hạt có nhiều quan sát, nhưng lớn hơn đối với các hạt chỉ có một hoặc hai quan sát.
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
Thật vậy, chúng ta có thể thấy điều này trực tiếp hơn bằng cách vẽ biểu đồ log-số quan sát so với độ lệch chuẩn ước tính và xem mối quan hệ là gần đúng tuyến tính.
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
So với lme4 trong R
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
Bảng sau đây tóm tắt kết quả.
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
Bảng này chỉ ra VI kết quả là trong vòng ~ 10% lme4 's. Điều này hơi đáng ngạc nhiên vì:
-
lme4được dựa trên phương pháp Laplace (không VI), - không có nỗ lực nào được thực hiện trong chuyên mục này để thực sự hội tụ,
- nỗ lực tối thiểu đã được thực hiện để điều chỉnh các siêu tham số,
- không có nỗ lực nào được thực hiện chính quy hóa hoặc xử lý trước dữ liệu (ví dụ: các tính năng trung tâm, v.v.).
Sự kết luận
Trong chuyên mục này, chúng tôi đã mô tả Mô hình hiệu ứng hỗn hợp tuyến tính tổng quát và chỉ ra cách sử dụng suy luận biến phân để phù hợp với chúng bằng cách sử dụng Xác suất TensorFlow. Mặc dù vấn đề đồ chơi chỉ có vài trăm mẫu huấn luyện, nhưng các kỹ thuật được sử dụng ở đây giống hệt với những gì cần thiết trên quy mô lớn.
