Dopasowywanie uogólnionych liniowych modeli efektów mieszanych za pomocą wnioskowania wariacyjnego

Zobacz na TensorFlow.org Uruchom w Google Colab Wyświetl źródło na GitHub Pobierz notatnik

zainstalować

zainstalować

Abstrakcyjny

W tej kolaboracji pokazujemy, jak dopasować uogólniony liniowy model efektów mieszanych za pomocą wnioskowania wariacyjnego w TensorFlow Probability.

Rodzina modeli

Uogólnione modele liniowe mieszane efekt (GLMM) są podobne do uogólnione modele liniowe (GLM) oprócz tego, że zawierają one szum próbki do konkretnego przewidywanego odpowiedzi liniowej. Jest to przydatne po części dlatego, że pozwala rzadko spotykanym funkcjom dzielić się informacjami z częściej spotykanymi funkcjami.

Jako proces generatywny, uogólniony liniowy model efektów mieszanych (GLMM) charakteryzuje się:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

gdzie:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

Innymi słowy, to mówi, że każda kategoria każdej grupy jest związane z próbki, \(\beta_{rc}\), z wielowymiarową normalne. Chociaż \(\beta_{rc}\) losowania są zawsze niezależne, są one tylko indentically dystrybuowane dla grupy \(r\): Anons istnieje dokładnie jeden \(\Sigma_r\) dla każdego \(r\in\{1,\ldots,R\}\).

Gdy affinely łączone z cechami próbki A w grupy (\(z_{r,i}\)), wynik jest próbka specyficzne szum na \(i\)-ty przewidywaną reakcję liniową (który jest poza tym \(x_i^\top\omega\)).

Kiedy szacujemy \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) jesteśmy zasadniczo szacowania ilości hałasu grupa przypadkowy efekt niesie które w przeciwnym razie zagłuszyć sygnał obecny w \(x_i^\top\omega\).

Istnieje wiele opcji dla \(\text{Distribution}\) i funkcji odwrotnej łącza , \(g^{-1}\). Typowe wybory to:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), a
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

Aby uzyskać więcej możliwości, zobacz tfp.glm moduł.

Wnioskowanie wariacyjne

Niestety, znalezienie maksymalne szacunki prawdopodobieństwa parametrów \(\beta,\{\Sigma_r\}_r^R\) wiąże się całki non-analitycznego. Aby obejść ten problem, zamiast tego

  1. Zdefiniować sparametryzowanego rodziny rozkładów (zwanego dalej „zastępczym gęstości”) oznaczony \(q_{\lambda}\) w załączniku.
  2. Znajdź parametry \(\lambda\) tak że \(q_{\lambda}\) jest blisko naszego prawdziwego docelowej denstiy.

Rodzina rozkładów będzie niezależny Gaussians właściwego wymiary, a przez „Blisko do naszego gęstości docelowej”, będziemy oznaczać „minimalizacji rozbieżności Kullback-Leiblera ”. Zobacz na przykład pkt 2.2 „wariacyjnymi Inference: przegląd dla Statystyków” za dobrze napisany wyliczania i motywacji. W szczególności pokazuje, że minimalizacja dywergencji KL jest równoważna minimalizacji dolnej granicy dowodów negatywnych (ELBO).

Problem z zabawkami

Gelman i wsp. (2007) „radon zbiór danych” to zbiór danych czasami wykorzystywane do wykazania podejścia do regresji. (Np, to ściśle związane PyMC3 blogu .) Radon zestawu danych zawiera pomiarów radonu wewnątrz podjętych w całych Stanach Zjednoczonych. Radon naturalnie ocurring radioaktywny gaz, który jest toksyczny w wysokich stężeniach.

Na potrzeby naszej demonstracji załóżmy, że jesteśmy zainteresowani potwierdzeniem hipotezy, że poziomy radonu są wyższe w gospodarstwach domowych zawierających piwnicę. Podejrzewamy również, że stężenie radonu ma związek z typem gleby, tj. kwestiami geograficznymi.

Aby sformułować to jako problem ML, spróbujemy przewidzieć poziomy log-radonu w oparciu o liniową funkcję podłogi, na której wykonano odczyt. Użyjemy również hrabstwa jako efektu losowego, uwzględniając w ten sposób wariancje wynikające z położenia geograficznego. Innymi słowy, użyjemy ogólny model liniowy mieszany-skutkowy .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

Zrobimy również szybkie sprawdzenie dostępności GPU:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

Uzyskaj zbiór danych:

Ładujemy zestaw danych z zestawów danych TensorFlow i wykonujemy lekkie wstępne przetwarzanie.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

Specjalizujemy się w rodzinie GLMM

W tej sekcji specjalizujemy się w przewidywaniu poziomu radonu w rodzinie GLMM. Aby to zrobić, najpierw rozważymy specjalny przypadek GLMM z efektem stałym:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

Model ten zakłada, że radon w dzienniku obserwacyjnym \(j\) IS (w oczekiwaniu) podlegającą podłodze z \(j\)th Odczytu dokonuje się na stałym poziomie, plus niektóre z osią. W pseudokodzie możemy napisać

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

istnieje waga dowiedział się za każdym piętrze oraz uniwersalny intercept perspektywie. Patrząc na pomiary radonu z poziomu 0 i 1, wygląda na to, że to może być dobry początek:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

png

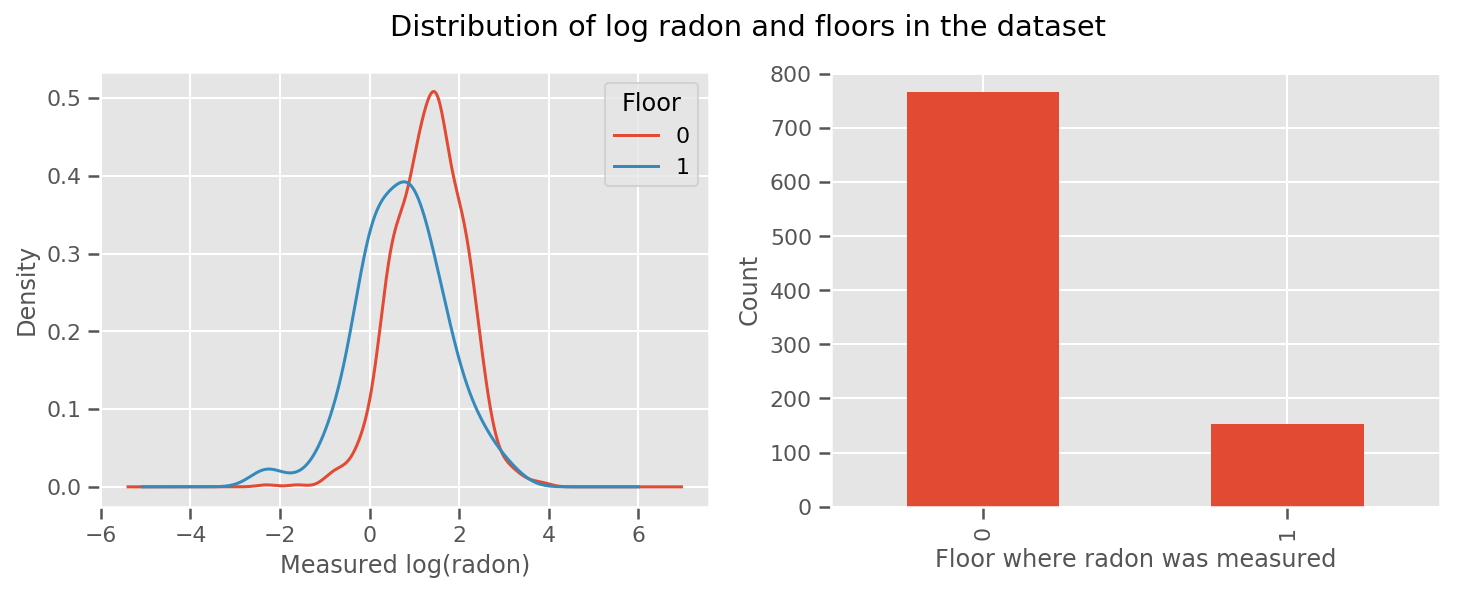
Uczynienie modelu nieco bardziej wyrafinowanym, włączając w to coś o geografii, jest prawdopodobnie jeszcze lepsze: radon jest częścią łańcucha rozpadu uranu, który może być obecny w ziemi, więc geografia wydaje się być kluczowa do wyjaśnienia.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

Znowu w pseudokodzie mamy

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

taki sam jak poprzednio, z wyjątkiem wagi specyficznej dla hrabstwa.

Przy wystarczająco dużym zbiorze uczącym jest to rozsądny model. Jednak biorąc pod uwagę nasze dane z Minnesoty, widzimy, że istnieje duża liczba hrabstw z niewielką liczbą pomiarów. Na przykład 39 z 85 powiatów ma mniej niż pięć obserwacji.

To motywuje do dzielenia siły statystycznej między wszystkimi naszymi obserwacjami w sposób, który jest zbieżny z powyższym modelem wraz ze wzrostem liczby obserwacji na hrabstwo.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

png

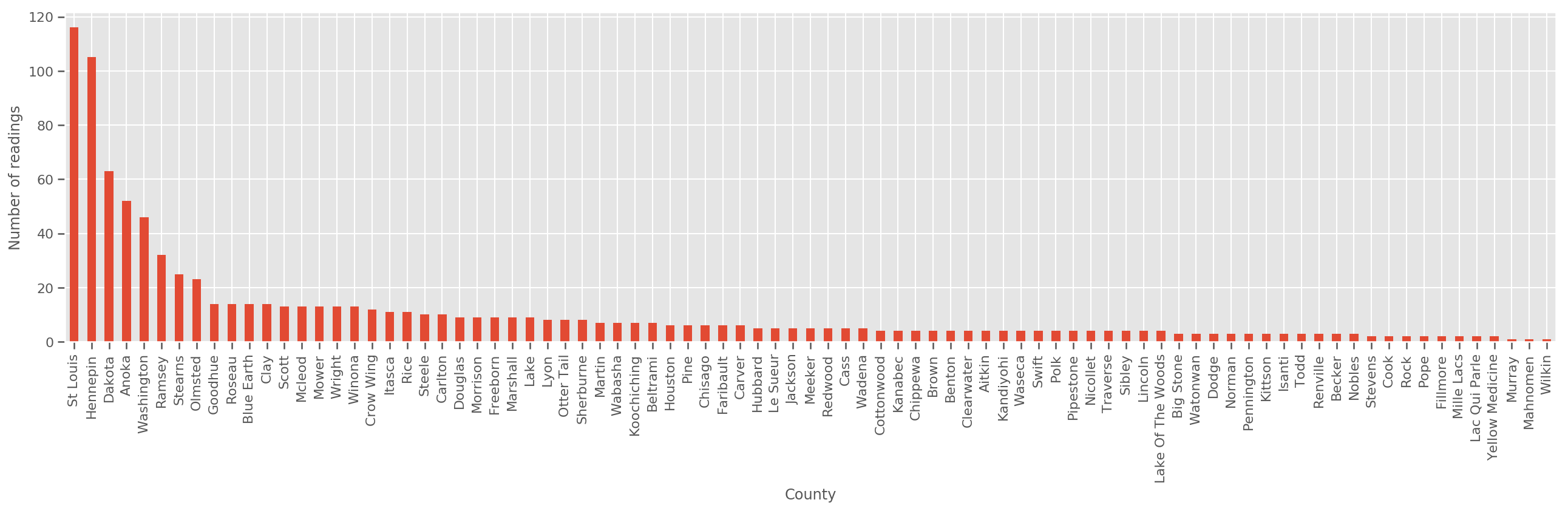
Jeśli mamy zmieścić tym modelu county_effect wektor prawdopodobnie skończyć zapamiętywania wyników dla powiatów, które miały tylko kilka próbek szkoleniowych, może przeuczenia i prowadzi do słabej uogólnienia.

GLMM oferują szczęśliwy środek dla dwóch powyższych GLMM. Możemy rozważyć dopasowanie

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

Model ten jest taki sam jak pierwszy, ale mamy stałych naszą prawdopodobieństwo być rozkład normalny, i będą dzielić wariancji we wszystkich okręgach przez (pojedynczy) zmiennej county_scale . W pseudokodzie,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

Będziemy wnioskować wspólną dystrybucję nad county_scale , county_mean , a random_effect Korzystanie z naszych zaobserwowanych danych. Globalna county_scale pozwala nam dzielić siły statystycznej całej powiatów: tych z wieloma obserwacjami zapewnić trafienie w wariancji powiatów z kilku obserwacji. Ponadto, w miarę gromadzenia większej ilości danych, model ten będzie zbieżny z modelem bez połączonej zmiennej ilościowej — nawet z tym zestawem danych dojdziemy do podobnych wniosków dotyczących najczęściej obserwowanych powiatów w obu modelach.

Eksperyment

Spróbujemy teraz dopasować powyższy GLMM za pomocą wnioskowania wariacyjnego w TensorFlow. Najpierw podzielimy dane na funkcje i etykiety.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

Określ model

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

Określ zastępczy tylny

Teraz ułożyła rodziny surogat \(q_{\lambda}\), gdzie parametry \(\lambda\) można trenować. W tym przypadku też rodzina jest niezależne wielowymiarowe rozkładu normalnego, po jednym dla każdego parametru, a \(\lambda = \{(\mu_j, \sigma_j)\}\), gdzie \(j\) indeksuje się cztery parametry.

Metoda, której używamy w celu dopasowania zastępczej rodzinie używa tf.Variables . Używamy również tfp.util.TransformedVariable wraz z Softplus ograniczyć parametry (wyszkolić) skalę, aby być dodatnia. Dodatkowo stosujemy Softplus do całego scale_prior , który jest dodatni parametr.

Te zmienne, które można trenować, inicjujemy z odrobiną fluktuacji, aby pomóc w optymalizacji.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

Zauważ, że ta komórka może być zastąpiony tfp.experimental.vi.build_factored_surrogate_posterior , na przykład:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

Wyniki

Przypomnijmy, że naszym celem jest zdefiniowanie praktycznie sparametryzowanej rodziny rozkładów, a następnie wybranie parametrów tak, aby uzyskać rozkład bliski naszemu rozkładowi docelowemu.

Zbudowaliśmy zastępczego rozkładu powyżej, i może korzystać tfp.vi.fit_surrogate_posterior , który akceptuje Optimizer i daną liczbę kroków, aby znaleźć parametry modelu zastępczego minimalizując Elbo negatywny (co corresonds do zminimalizowania rozbieżności między Kullback-Liebler surogatu i dystrybucji docelowej).

Zwracana jest wartość ujemna ELBO na każdym kroku, a dystrybucje w surrogate_posterior zostaną zaktualizowane znaleźć parametry przez optymalizator.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

png

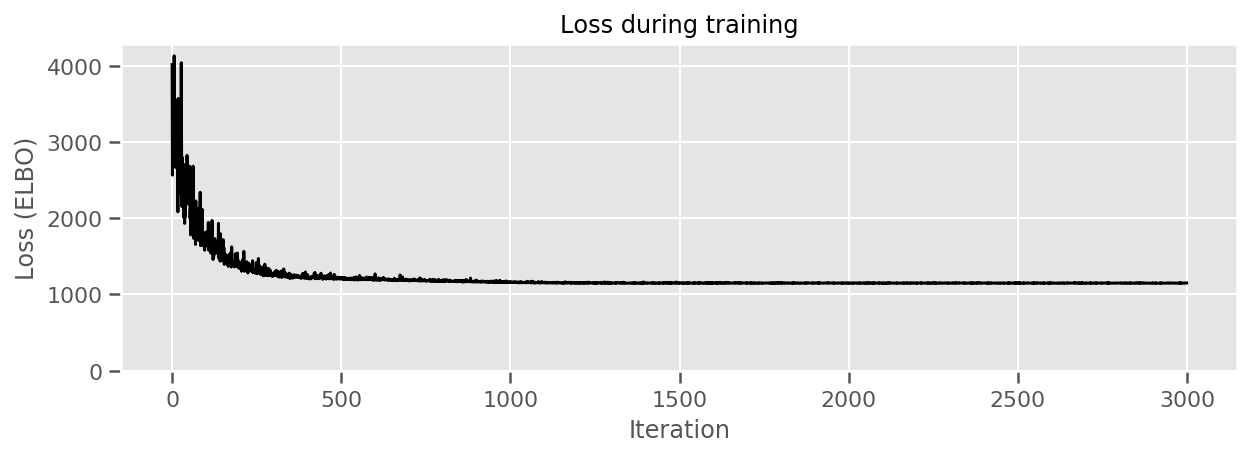
Możemy wykreślić oszacowane średnie efekty hrabstwa wraz z niepewnością tej średniej. Uporządkowaliśmy to według liczby obserwacji, z największą po lewej stronie. Zauważ, że niepewność jest mała dla hrabstw z wieloma obserwacjami, ale jest większa dla hrabstw, które mają tylko jedną lub dwie obserwacje.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

png

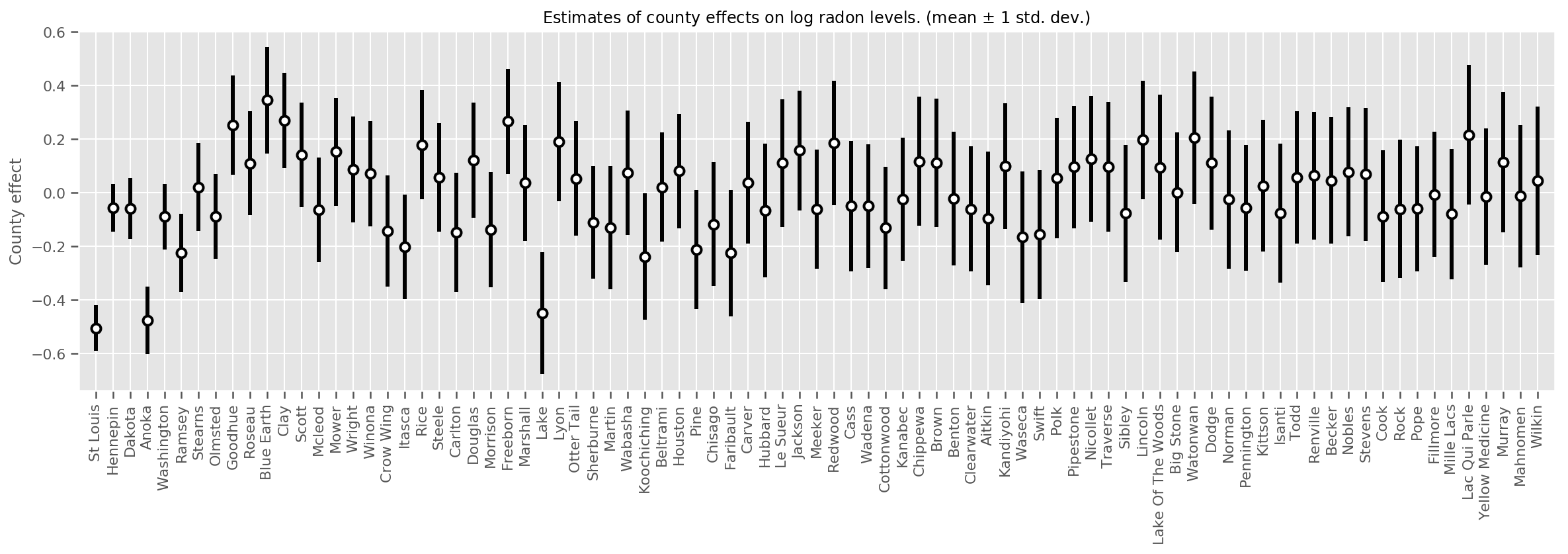
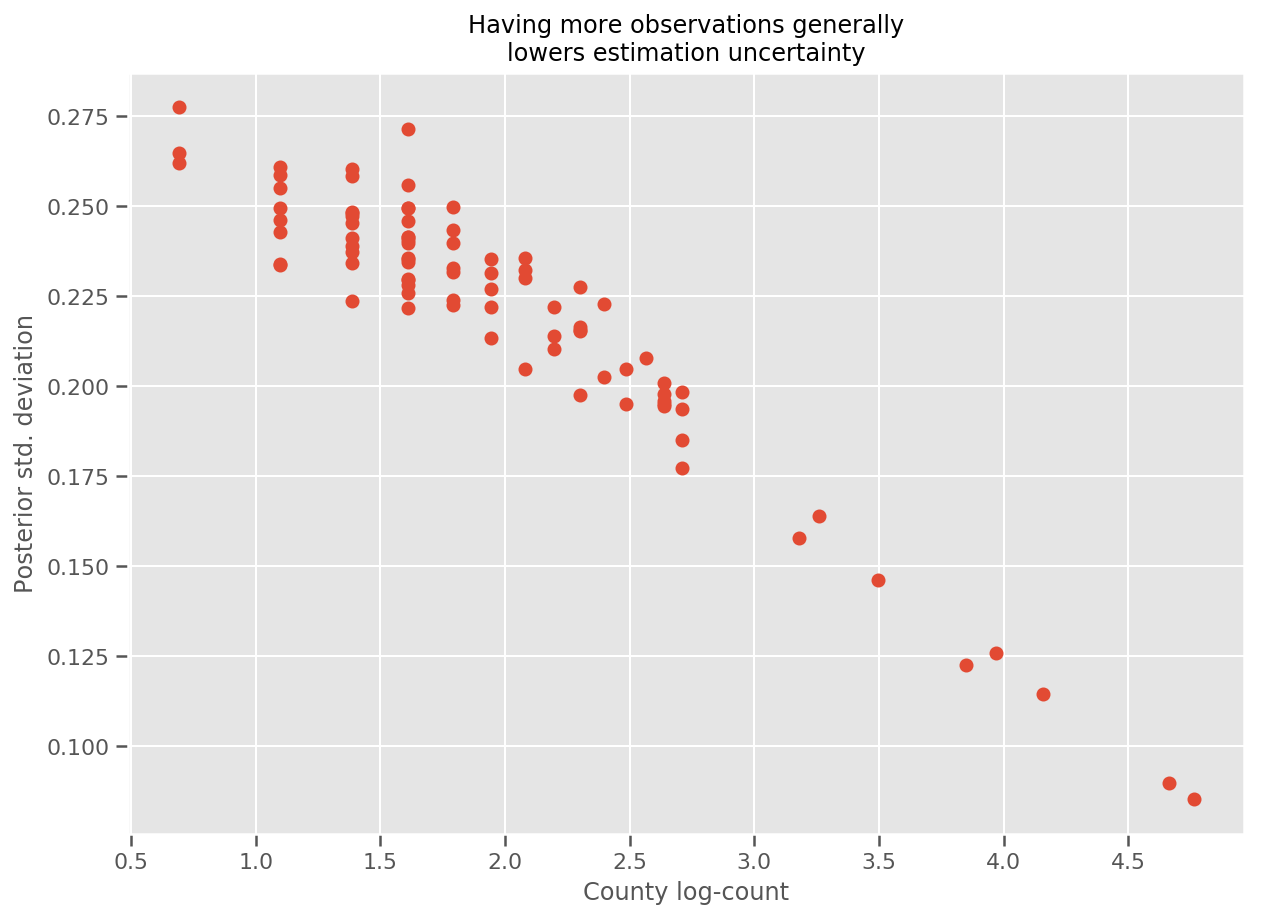
Rzeczywiście, możemy to zobaczyć bardziej bezpośrednio, wykreślając liczbę logarytmiczną obserwacji w stosunku do szacowanego odchylenia standardowego i widzimy, że zależność jest w przybliżeniu liniowa.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

png

W stosunku do lme4 w R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

Poniższa tabela podsumowuje wyniki.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

Tabela ta wskazuje, że VI Wyniki znajdują się w ~ 10% z lme4 „s. Jest to nieco zaskakujące, ponieważ:

  • lme4 oparta jest na metodzie Laplace'a (nie VI),
  • w tej kolaboracji nie podjęto żadnych wysiłków, aby rzeczywiście się zbliżyć,
  • minimalny wysiłek włożono w dostrojenie hiperparametrów,
  • nie podjęto żadnych wysiłków, aby uregulować lub wstępnie przetworzyć dane (np. funkcje centrum itp.).

Wniosek

W tym kolaboracji opisaliśmy uogólnione liniowe modele efektów mieszanych i pokazaliśmy, jak używać wnioskowania wariacyjnego, aby dopasować je za pomocą prawdopodobieństwa przepływu przez Tensor. Chociaż problem z zabawkami dotyczył tylko kilkuset próbek szkoleniowych, zastosowane tutaj techniki są identyczne z tym, co jest potrzebne na dużą skalę.