 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Install
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
Install
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
Abstrak
Dalam colab ini, kami mendemonstrasikan cara menyesuaikan model efek campuran linier umum menggunakan inferensi variasi dalam Probabilitas TensorFlow.
Keluarga Model
Generalized linear model campuran-efek (GLMM) mirip dengan umum linear model (GLM) kecuali bahwa mereka menggabungkan suara sampel tertentu ke respon linear diprediksi. Ini berguna sebagian karena memungkinkan fitur yang jarang terlihat untuk berbagi informasi dengan fitur yang lebih sering terlihat.
Sebagai proses generatif, Generalized Linear Mixed-effect Model (GLMM) dicirikan oleh:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
di mana:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
Dengan kata lain, ini mengatakan bahwa setiap kategori masing-masing kelompok terkait dengan sampel, \(\beta_{rc}\), dari normal multivariat. Meskipun \(\beta_{rc}\) menarik selalu independen, mereka hanya indentically didistribusikan untuk kelompok \(r\): pemberitahuan ada tepat satu \(\Sigma_r\) untuk setiap \(r\in\{1,\ldots,R\}\).
Ketika affinely dikombinasikan dengan fitur kelompok sampel ini (\(z_{r,i}\)), hasilnya adalah contoh spesifik noise pada \(i\)-th diprediksi respon linear (yang dinyatakan \(x_i^\top\omega\)).
Ketika kami memperkirakan \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) kita pada dasarnya memperkirakan jumlah suara kelompok acak-efek membawa yang dinyatakan akan meredam hadir sinyal di \(x_i^\top\omega\).
Ada berbagai pilihan untuk \(\text{Distribution}\) dan fungsi link terbalik , \(g^{-1}\). Pilihan umum adalah:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), dan,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
Untuk kemungkinan lebih lanjut, lihat tfp.glm modul.
Inferensi Variasi
Sayangnya, menemukan perkiraan kemungkinan maksimum parameter \(\beta,\{\Sigma_r\}_r^R\) memerlukan terpisahkan non-analitis. Untuk menghindari masalah ini, kita sebagai gantinya
- Mendefinisikan sebuah keluarga parameter distribusi (yang "pengganti density"), dilambangkan \(q_{\lambda}\) dalam lampiran.
- Cari parameter \(\lambda\) sehingga \(q_{\lambda}\) dekat denstiy target kami benar.
Keluarga distribusi akan Gaussians independen dari dimensi yang tepat, dan dengan "dekat dengan kepadatan target kami", kita akan berarti "meminimalkan perbedaan Kullback-Leibler ". Lihat, misalnya Pasal 2.2 dari "Variasional Inference: Sebuah Tinjauan untuk Statistik" untuk derivasi ditulis dengan baik dan motivasi. Secara khusus, ini menunjukkan bahwa meminimalkan divergensi KL sama dengan meminimalkan batas bawah bukti negatif (ELBO).
Masalah mainan
Gelman et al. (2007) "radon dataset" adalah dataset kadang-kadang digunakan untuk menunjukkan pendekatan untuk regresi. (Misalnya, terkait erat ini posting PyMC3 blog .) The radon dataset berisi pengukuran dalam ruangan Radon diambil di seluruh Amerika Serikat. Radon secara alami ocurring gas radioaktif yang beracun dalam konsentrasi tinggi.
Untuk demonstrasi kami, anggaplah kami tertarik untuk memvalidasi hipotesis bahwa tingkat Radon lebih tinggi di rumah tangga yang memiliki ruang bawah tanah. Kami juga menduga konsentrasi Radon terkait dengan jenis tanah, yaitu, masalah geografi.
Untuk membingkai ini sebagai masalah ML, kami akan mencoba memprediksi level log-radon berdasarkan fungsi linier lantai tempat pembacaan dilakukan. Kami juga akan menggunakan county sebagai efek acak dan dengan demikian memperhitungkan varians karena geografi. Dengan kata lain, kita akan menggunakan model campuran efek linear umum .
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
Kami juga akan melakukan pemeriksaan cepat untuk ketersediaan GPU:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
Dapatkan Kumpulan Data:
Kami memuat set data dari set data TensorFlow dan melakukan prapemrosesan ringan.
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
Mengkhususkan Keluarga GLMM
Di bagian ini, kami mengkhususkan keluarga GLMM untuk tugas memprediksi tingkat radon. Untuk melakukan ini, pertama-tama kita pertimbangkan kasus khusus efek tetap dari GLMM:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
Model ini berpendapat bahwa radon log dalam pengamatan \(j\) adalah (dengan harapan) diatur oleh lantai yang \(j\)membaca th diambil pada, ditambah beberapa konstan intercept. Dalam pseudocode, kita mungkin menulis
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
ada bobot belajar untuk setiap lantai dan universal intercept jangka. Melihat pengukuran radon dari lantai 0 dan 1, sepertinya ini awal yang baik:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
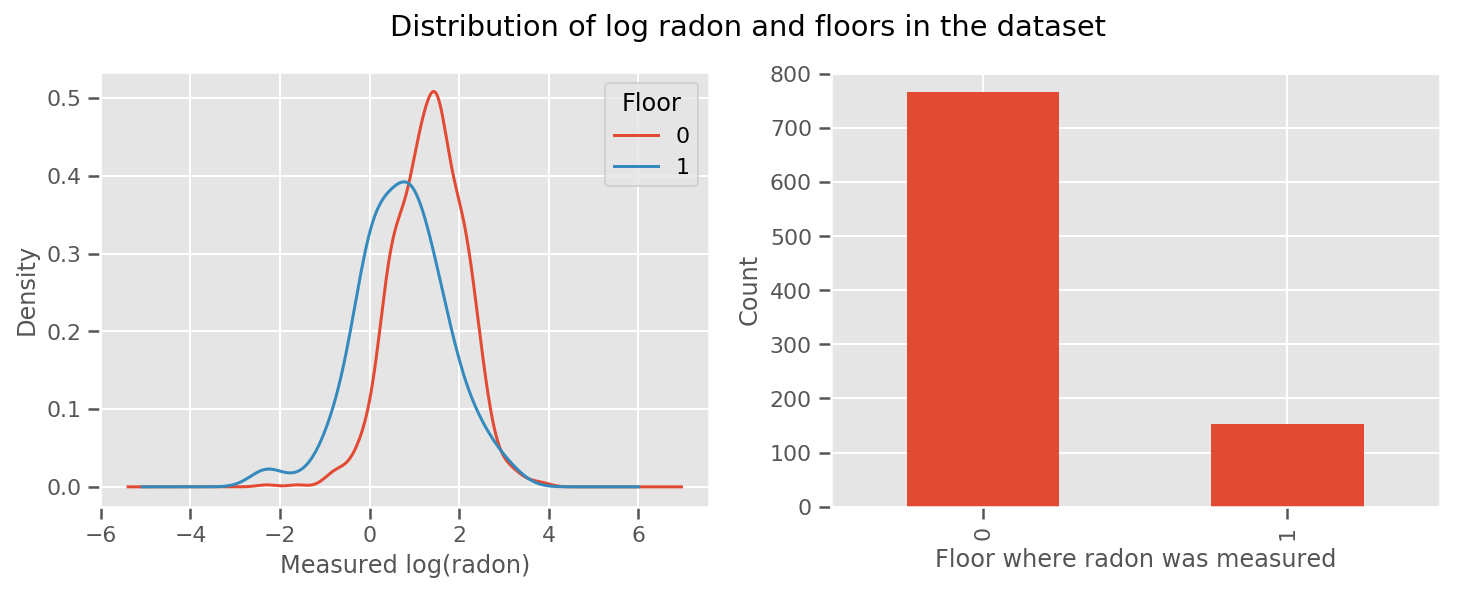
Untuk membuat modelnya sedikit lebih canggih, termasuk sesuatu tentang geografi mungkin lebih baik: radon adalah bagian dari rantai peluruhan uranium, yang mungkin ada di dalam tanah, jadi geografi tampaknya menjadi kunci untuk diperhitungkan.
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
Sekali lagi, dalam pseudocode, kita memiliki
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
sama seperti sebelumnya kecuali dengan bobot khusus daerah.
Mengingat set pelatihan yang cukup besar, ini adalah model yang masuk akal. Namun, berdasarkan data kami dari Minnesota, kami melihat bahwa ada sejumlah besar kabupaten dengan sejumlah kecil pengukuran. Misalnya, 39 dari 85 kabupaten memiliki kurang dari lima pengamatan.
Ini memotivasi berbagi kekuatan statistik di antara semua pengamatan kami, dengan cara yang menyatu dengan model di atas saat jumlah pengamatan per kabupaten meningkat.
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
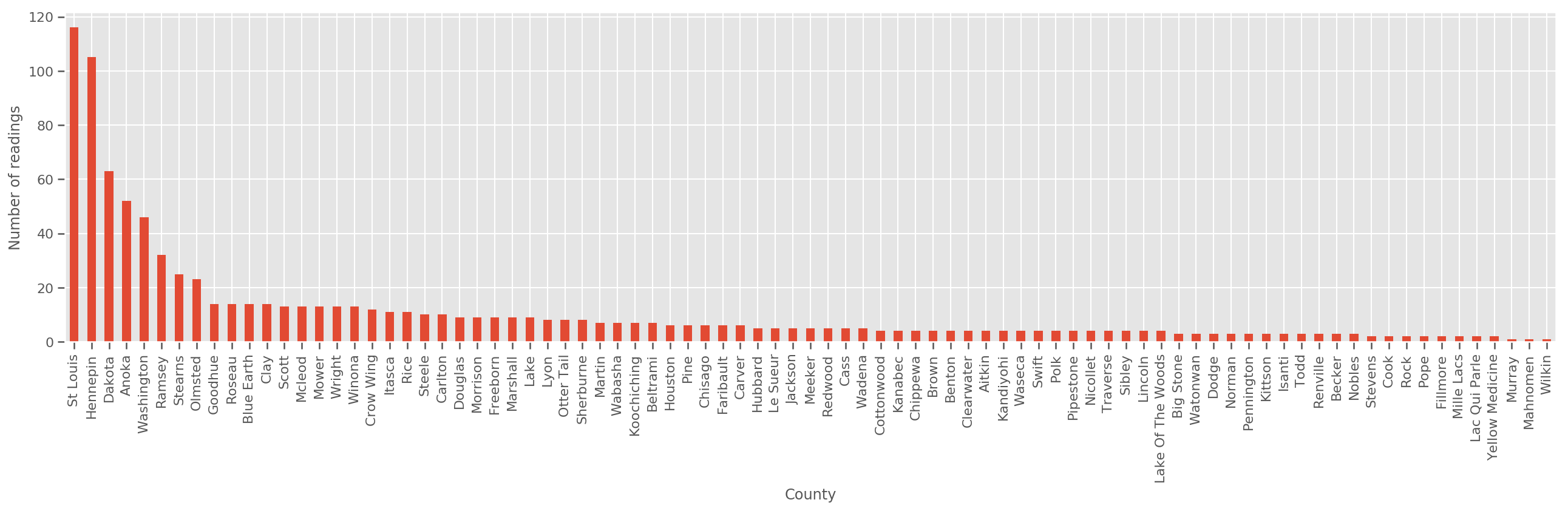
Jika kita cocok dengan model ini, county_effect vektor kemungkinan akan berakhir menghafal hasil untuk kabupaten yang memiliki hanya beberapa sampel pelatihan, mungkin overfitting dan menyebabkan generalisasi yang buruk.
GLMM menawarkan tengah yang menyenangkan untuk dua GLM di atas. Kami mungkin mempertimbangkan untuk menyesuaikan
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
Model ini adalah sama seperti yang pertama, tapi kami telah tetap kemungkinan kami untuk menjadi distribusi normal, dan akan berbagi varians di semua kabupaten melalui (single) variabel county_scale . Dalam kode semu,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
Kami akan menyimpulkan distribusi bersama atas county_scale , county_mean , dan random_effect menggunakan data yang diamati kami. Global county_scale memungkinkan kita untuk berbagi kekuatan statistik di seluruh kabupaten: mereka yang banyak pengamatan memberikan hit di varians dari kabupaten dengan beberapa pengamatan. Selanjutnya, saat kami mengumpulkan lebih banyak data, model ini akan menyatu dengan model tanpa variabel skala gabungan - bahkan dengan kumpulan data ini, kami akan sampai pada kesimpulan serupa tentang kabupaten yang paling banyak diamati dengan salah satu model.
Percobaan
Sekarang kita akan mencoba menyesuaikan GLMM di atas menggunakan inferensi variasi di TensorFlow. Pertama kita akan membagi data menjadi fitur dan label.
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
Tentukan Model
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
Tentukan pengganti posterior
Kita sekarang mengumpulkan pengganti keluarga \(q_{\lambda}\), di mana parameter \(\lambda\) yang dilatih. Dalam hal ini, keluarga kami adalah independen distribusi multivariat normal, satu untuk setiap parameter, dan \(\lambda = \{(\mu_j, \sigma_j)\}\), di mana \(j\) indeks empat parameter.
Metode yang kami gunakan agar sesuai dengan pengganti penggunaan keluarga tf.Variables . Kami juga menggunakan tfp.util.TransformedVariable bersama dengan Softplus untuk membatasi parameter (dilatih) skala menjadi positif. Selain itu, kami menerapkan Softplus ke seluruh scale_prior , yang merupakan parameter yang positif.
Kami menginisialisasi variabel yang dapat dilatih ini dengan sedikit jitter untuk membantu pengoptimalan.
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
Perhatikan bahwa sel ini bisa diganti dengan tfp.experimental.vi.build_factored_surrogate_posterior , seperti di:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
Hasil
Ingatlah bahwa tujuan kami adalah untuk menentukan keluarga distribusi yang memiliki parameter penurut, dan kemudian memilih parameter sehingga kami memiliki distribusi yang dapat dilacak yang dekat dengan distribusi target kami.
Kami telah membangun distribusi pengganti atas, dan dapat menggunakan tfp.vi.fit_surrogate_posterior , yang menerima sebuah optimizer dan sejumlah diberikan langkah-langkah untuk menemukan parameter untuk model pengganti meminimalkan ELBO negatif (yang corresonds untuk meminimalkan perbedaan Kullback-Liebler antara pengganti dan distribusi target).
Nilai kembali adalah ELBO negatif pada setiap langkah, dan distribusi di surrogate_posterior akan telah diperbarui dengan parameter ditemukan oleh optimizer.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
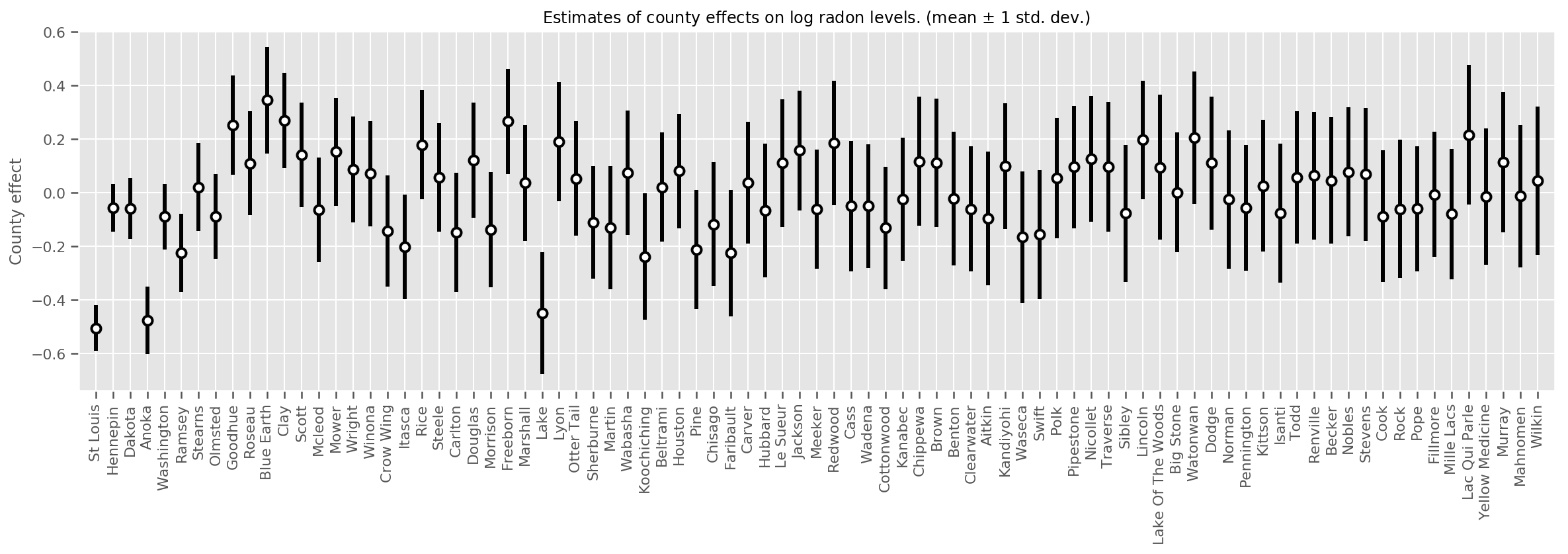
Kita dapat memplot perkiraan efek daerah rata-rata, bersama dengan ketidakpastian rata-rata itu. Kami telah memesan ini dengan jumlah pengamatan, dengan yang terbesar di sebelah kiri. Perhatikan bahwa ketidakpastian kecil untuk kabupaten dengan banyak pengamatan, tetapi lebih besar untuk kabupaten yang hanya memiliki satu atau dua pengamatan.
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
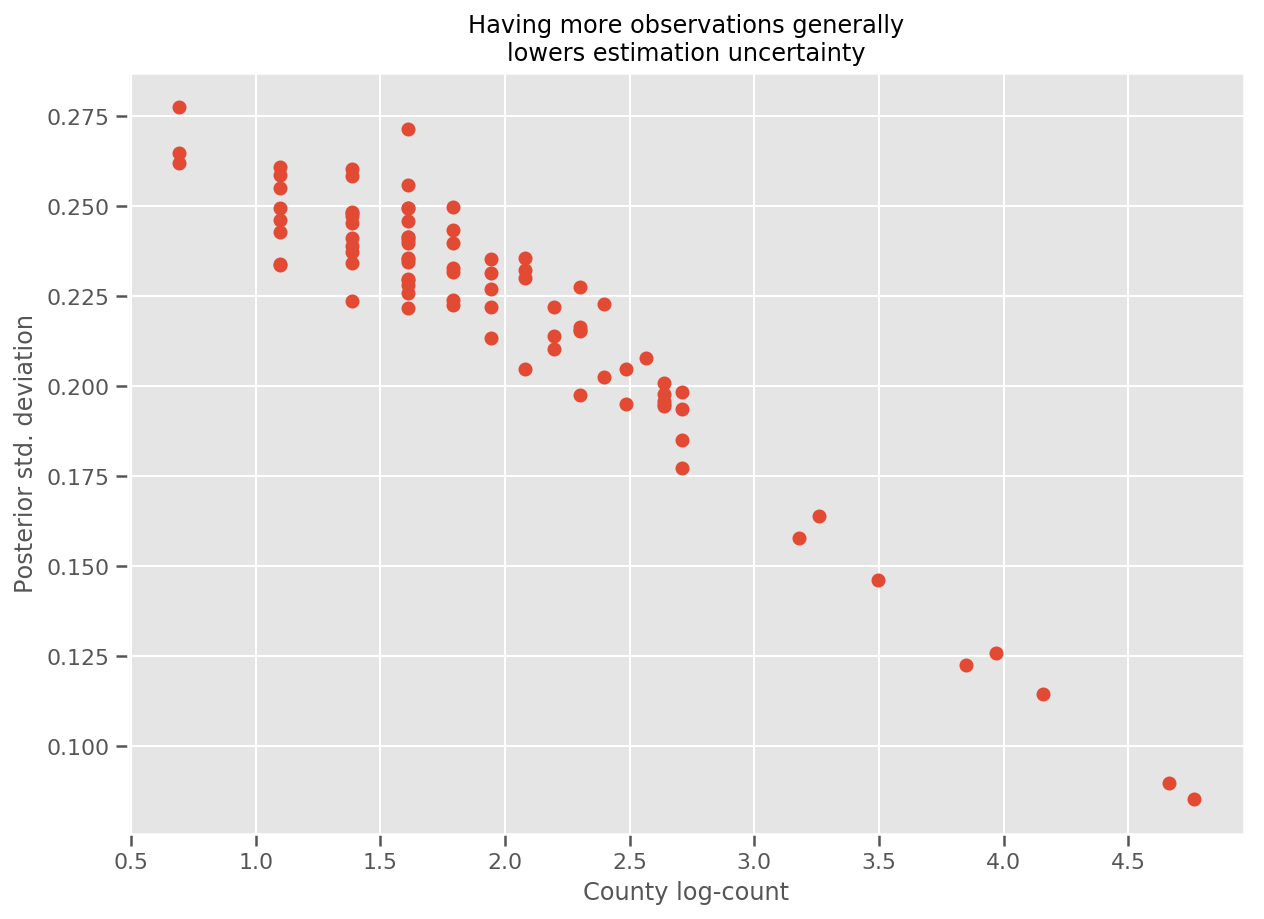
Memang, kita dapat melihat ini secara lebih langsung dengan memplot jumlah log pengamatan terhadap standar deviasi yang diperkirakan, dan melihat hubungannya mendekati linier.
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
Dibandingkan dengan lme4 di R
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
Tabel berikut merangkum hasilnya.
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
Tabel ini menunjukkan VI hasilnya dalam ~ 10% dari lme4 's. Ini agak mengejutkan karena:
-
lme4didasarkan pada metode Laplace (tidak VI), - tidak ada upaya yang dilakukan dalam colab ini untuk benar-benar bertemu,
- upaya minimal dilakukan untuk menyetel hyperparameters,
- tidak ada upaya yang dilakukan untuk mengatur atau memproses data sebelumnya (misalnya, fitur pusat, dll.).
Kesimpulan
Dalam kolaborasi ini kami menjelaskan Model Efek Campuran Linear Umum dan menunjukkan cara menggunakan inferensi variasi agar sesuai dengannya menggunakan Probabilitas TensorFlow. Meskipun masalah mainan hanya memiliki beberapa ratus sampel pelatihan, teknik yang digunakan di sini identik dengan apa yang dibutuhkan dalam skala besar.
