התאמת דגמים מעורבים ליניאריים כלליים באמצעות אפקט מעורב

הצג באתר TensorFlow.org הפעל בגוגל קולאב צפה במקור ב-GitHub הורד מחברת

להתקין

להתקין

תַקצִיר

בקולאב זה אנו מדגימים כיצד להתאים מודל כללי של אפקטים מעורבים ליניארי תוך שימוש בהסקת וריאציות בהסתברות TensorFlow.

משפחת דוגמניות

Generalized ליניארי מודלים של השפעות משולבות (GLMM) הדומים כלליים ליניארי מודלים (GLM) מלבד העובדה שהם משלבים רעש ספציפי מדגם לתוך התגובה ליניארי חזה. זה שימושי בין השאר מכיוון שהוא מאפשר לתכונות שנראו נדירות לשתף מידע עם תכונות נפוצות יותר.

כתהליך יצירתי, מודל ליניארי מעורב-אפקט כללי (GLMM) מאופיין ב:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

איפה:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

במילים אחרות, זה אומר כי בכל קטגוריה של כל קבוצה קשורה מדגם, \(\beta_{rc}\), ממשפחה נורמלית רב משתנים. למרות \(\beta_{rc}\) שואבת תמיד עצמאית, הם רק מופץ indentically עבור קבוצת \(r\): הודעה יש בדיוק אחד \(\Sigma_r\) לכל \(r\in\{1,\ldots,R\}\).

בשילוב אפיני עם תכונות של קבוצת המדגם (\(z_{r,i}\)), והתוצאה היא רעש מדגם ספציפי על \(i\)ה- יצא ניבאו תגובה ליניארי (המהווה אחרת \(x_i^\top\omega\)).

כאשר אנו מעריכים \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) אנחנו בעצם מעריכים את כמות רעש קבוצה אקראית-אפקט נושאת שאחרת להטביע את הווה האות ב \(x_i^\top\omega\).

יש מגוון של אפשרויות עבור \(\text{Distribution}\) ואת הפונקציה הקישור הפוך , \(g^{-1}\). הבחירות הנפוצות הן:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), ו,
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

לקבלת אפשרויות יותר, לראות את tfp.glm מודול.

הסקה וריאציונית

למרבה הצער, למצוא את כל הערכות סבירות מקסימלית של פרמטרים \(\beta,\{\Sigma_r\}_r^R\) כרוך הלא אנליטי נפרד. כדי לעקוף את הבעיה הזו, אנחנו במקום זאת

  1. הגדר משפחה עם פרמטרים של הפצות (להלן: "צפיפות פונדקאית"), מסומן \(q_{\lambda}\) בנספח.
  2. מצא פרמטרים \(\lambda\) כך \(q_{\lambda}\) קרוב denstiy היעד האמיתי שלנו.

משפחת הפצות יהיה Gaussians עצמאית של המידות הנכונות, ועל ידי "קרוב צפיפות היעד שלנו", אנו מתכוונים "מזעור הבדלי Kullback-ליבלר ". ראה, למשל סעיף 2.2 של "הסקת וריאציה: סקירה עבור סטטיסטיקאים" לגזירה כתוב היטב ומוטיבציה. בפרט, זה מראה שצמצום הפער ב-KL שווה ערך למזעור הראיות השליליות התחתון (ELBO).

בעיית צעצוע

ואח 'גלמן. של (2007) "הנתונים ראדון" הוא במערך לפעמים משמש כדי להדגים גישות עבור רגרסיה. (למשל, קשורה קשר הדוק זה הבלוג PyMC3 פוסט .) בסיס הנתונים ראדון מכיל מדידות מקורה של ראדון נלקח ברחבי ארצות הברית. ראדון הוא טבעי ocurring גז רדיואקטיבי המהווה רעילים בריכוזים גבוהים.

לצורך ההדגמה שלנו, נניח שאנו מעוניינים לאמת את ההשערה שרמות הראדון גבוהות יותר במשקי בית המכילים מרתף. אנו גם חושדים שריכוז הראדון קשור לסוג הקרקע, כלומר, חשוב לגיאוגרפיה.

כדי למסגר זאת כבעיית ML, ננסה לחזות את רמות הלוג-ראדון בהתבסס על פונקציה ליניארית של הרצפה שעליה בוצעה הקריאה. אנו גם נשתמש במחוז כאפקט אקראי ובכך נביא בחשבון את השונות הנובעות מגיאוגרפיה. במילים אחרות, אנו נשתמש במודל השפעות משולבות ליניארי כללית .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

אנו גם נבצע בדיקה מהירה של זמינות של GPU:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

השג מערך נתונים:

אנו טוענים את מערך הנתונים ממערכי נתונים של TensorFlow ועושים עיבוד מוקדם קל.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

מתמחה במשפחת GLMM

בחלק זה, אנו מתמחים את משפחת GLMM למשימה של חיזוי רמות ראדון. לשם כך, תחילה נבחן את המקרה המיוחד בעל אפקט קבוע של GLMM:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

טוען מודל זה כי ראדון היכנס תצפית \(j\) הוא (ב ציפייה) נשלט על ידי הרצפה \(j\)ה קריאה נלקחה על, בתוספת כמה ליירט מתמיד. בפסאודוקוד, אולי נכתוב

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

יש משקל למד במשך כול רצפה אוניוורסלי intercept לטווח. כשמסתכלים על מדידות הראדון מקומה 0 ו-1, נראה שזו יכולה להיות התחלה טובה:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

png

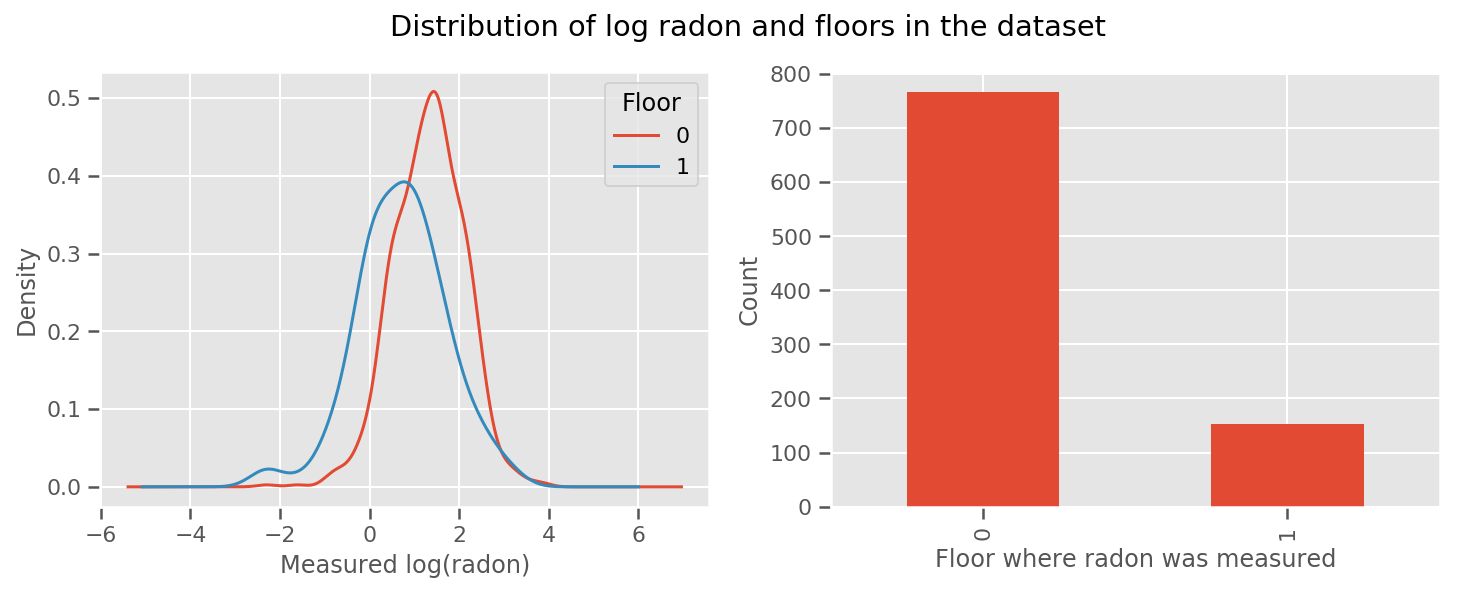
כדי להפוך את המודל לקצת יותר מתוחכם, לכלול משהו בגיאוגרפיה זה כנראה אפילו טוב יותר: ראדון הוא חלק משרשרת הריקבון של אורניום, שעשוי להיות קיים באדמה, כך שנראה שהגיאוגרפיה חשובה להתייחס אליה.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

שוב, בפסאודוקוד, יש לנו

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

זהה לקודם למעט עם משקל ספציפי למחוז.

בהינתן מערך אימונים גדול מספיק, זהו דגם סביר. עם זאת, בהתחשב בנתונים שלנו ממינסוטה, אנו רואים שיש מספר רב של מחוזות עם מספר קטן של מדידות. לדוגמה, ל-39 מתוך 85 מחוזות יש פחות מחמש תצפיות.

זה מניע שיתוף כוח סטטיסטי בין כל התצפיות שלנו, באופן שמתכנס למודל שלעיל ככל שמספר התצפיות למחוז גדל.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

png

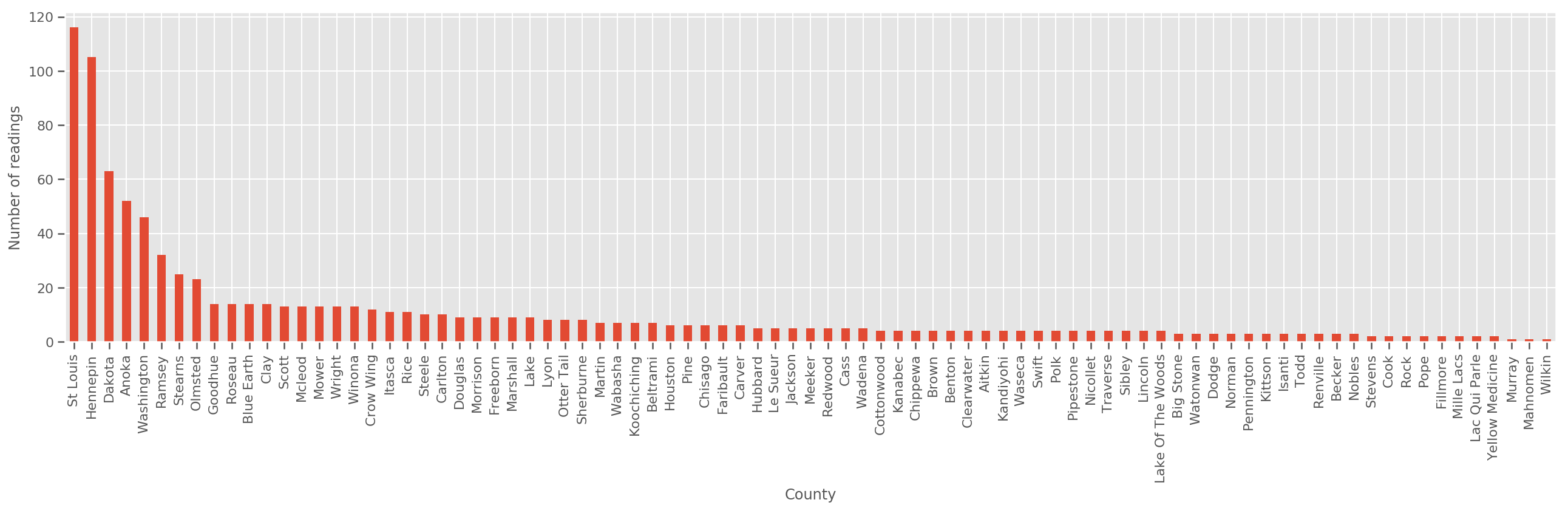
אם אנחנו מתאימים לדגם זה, county_effect הווקטור יסתיים עד סביר לשנן את התוצאות עבור מחוזות אשר היו רק כמה דוגמאות אימונים, אולי overfitting ומוביל הכללה עניה.

GLMM's מציעות אמצע שמח לשני ה-GLMs לעיל. אולי נשקול להתאים

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

מודל זה זהה הראשון, אבל יש לנו קבוע הסבירות שלנו להיות התפלגות נורמלית, ויחלקו אותו השונות בכל מחוזות באמצעות המשתנה (יחיד) county_scale . בפסאודוקוד,

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

אנו להסיק את ההפצה המשותפת מעל county_scale , county_mean , ואת random_effect שימוש בנתונים נצפים שלנו. לגלובלי county_scale מאפשר לנו לחלוק כוח סטטיסטי על פני מחוזות: בעלי תצפיות רבות לספק להיט בבית השונה של מחוזות עם כמה תצפיות. יתר על כן, ככל שנאסף נתונים נוספים, מודל זה יתכנס למודל ללא משתנה קנה מידה מאוחד - אפילו עם מערך הנתונים הזה, נגיע למסקנות דומות לגבי המחוזות הנצפים ביותר עם כל אחד מהמודלים.

לְנַסוֹת

כעת ננסה להתאים את ה-GLMM הנ"ל באמצעות הסקת וריאציות ב-TensorFlow. ראשית נחלק את הנתונים לתכונות ותוויות.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

ציין דגם

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

ציין פונדקאי אחורי

אנחנו עכשיו להרכיב פונדקאית המשפחה \(q_{\lambda}\), שבו הפרמטרים \(\lambda\) הם שאפשר לאלף. במקרה זה, המשפחה שלנו היא התפלגות נורמלית רב משתנים בלתי תלויים, אחד לכל פרמטר, ו \(\lambda = \{(\mu_j, \sigma_j)\}\), שבו \(j\) אינדקסים ארבעת הפרמטרים.

השיטה שאנו משתמשים בו כדי להתאים את השימושים משפחה פונדקאית tf.Variables . בנוסף, אנו משתמשים tfp.util.TransformedVariable יחד עם Softplus כדי להגביל את הפרמטרים מידה (שאפשר לאלף) להיות חיובי. בנוסף, אנחנו מיישמים Softplus אל כולו scale_prior , המהווה פרמטר חיובי.

אנו מאתחלים את המשתנים הניתנים לאימון עם מעט ריצוד כדי לסייע באופטימיזציה.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

הערה כי תא זה יכול להיות מוחלף עם tfp.experimental.vi.build_factored_surrogate_posterior , כמו:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

תוצאות

נזכיר שהמטרה שלנו היא להגדיר משפחת התפלגויות עם פרמטרים ניתנים למעקב, ולאחר מכן לבחור פרמטרים כך שתהיה לנו תפוצה ניתנת לבדיקה הקרובה להתפלגות היעד שלנו.

בנינו חלוק הפונדקאית לעיל, והוא יכולים להשתמש tfp.vi.fit_surrogate_posterior , המקבלת מייעל ו מספר נתון של צעדים כדי למצוא את הפרמטרים עבור המודל הפונדקאי מזעור אלבו השלילי (אשר corresonds כדי למזער את הבדלי Kullback-ליבלר בין הפונדקאית והתפלגות היעד).

הערך המוחזר הוא אלבו השלילי בכול שלב, ואת ההפצות ב surrogate_posterior תעודכנה עם הפרמטרים שנמצאו על ידי הייעול.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

png

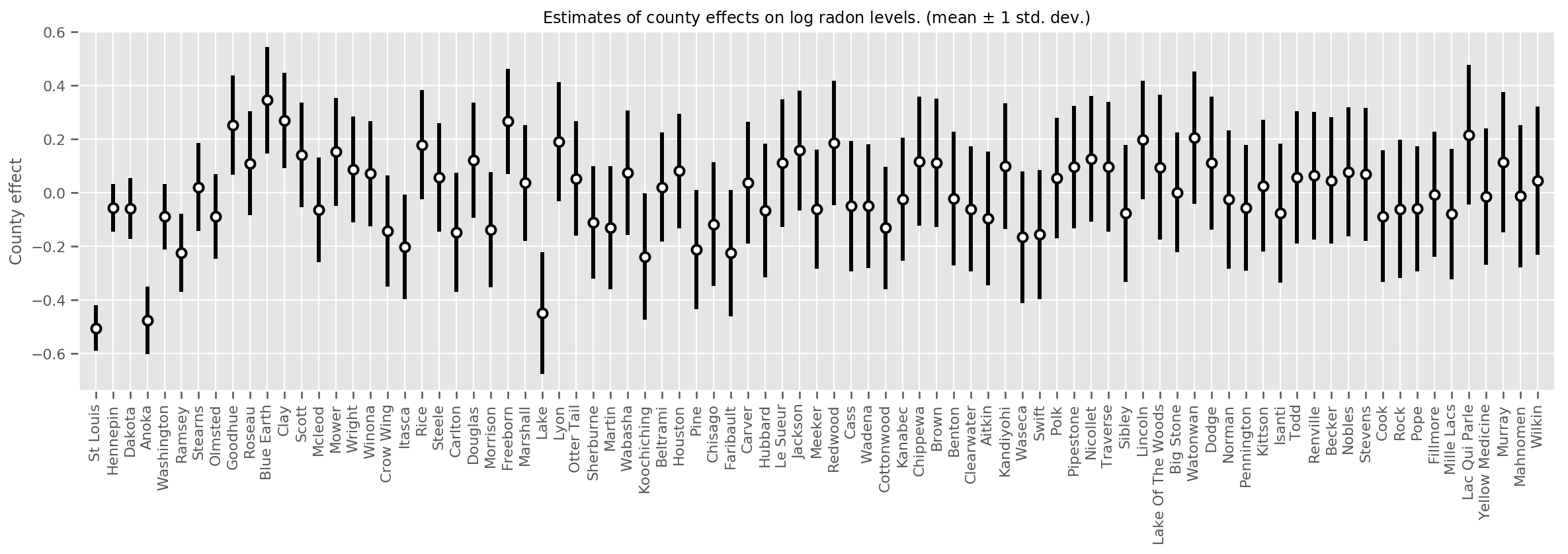
אנו יכולים לשרטט את ההשפעות הממוצעות של המחוז, יחד עם אי הוודאות של ממוצע זה. סדרנו את זה לפי מספר התצפיות, כשהגדולה ביותר משמאל. שימו לב שאי הוודאות קטנה עבור המחוזות עם תצפיות רבות, אך היא גדולה יותר עבור המחוזות שיש להם רק תצפית אחת או שתיים.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

png

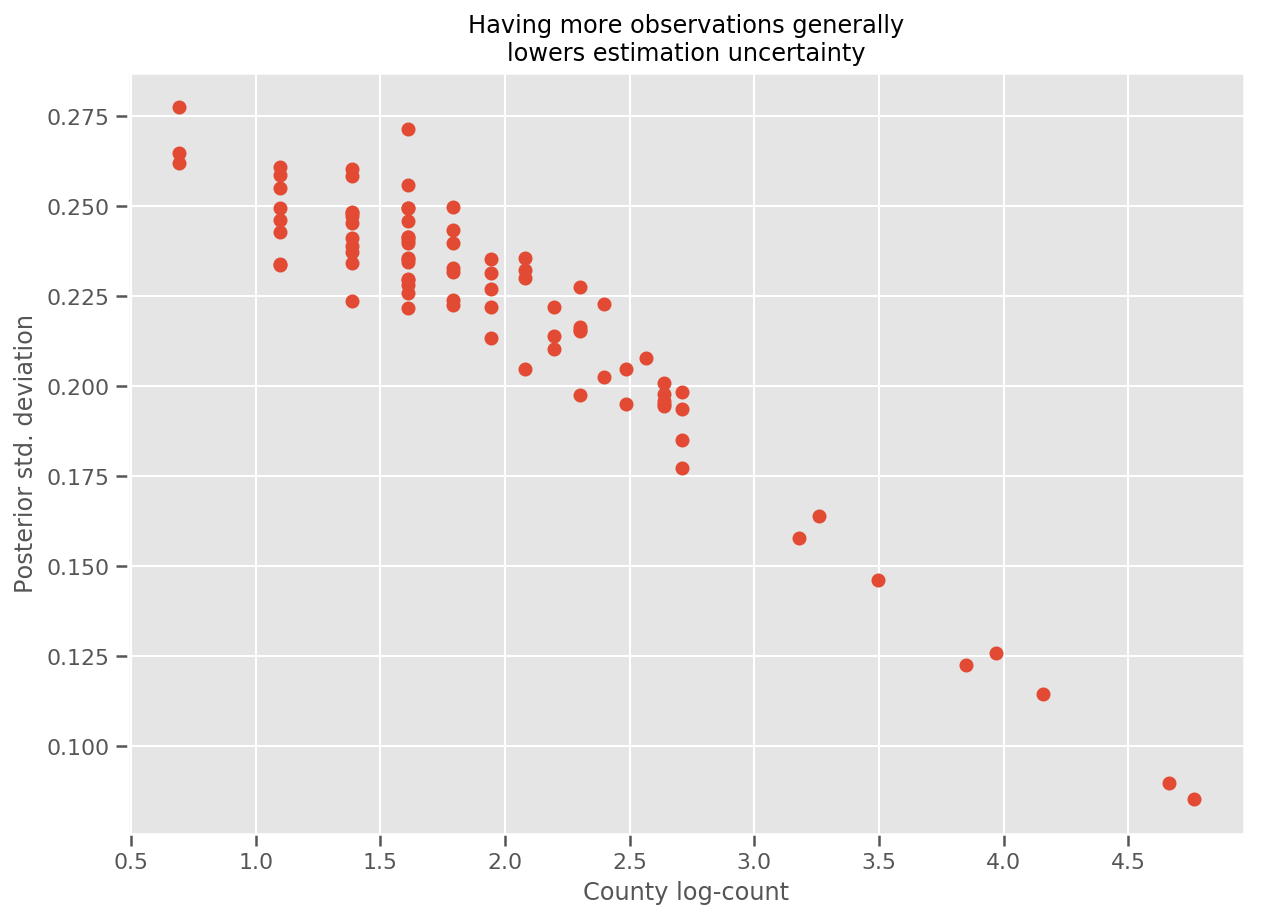
ואכן, אנו יכולים לראות זאת בצורה ישירה יותר על-ידי התווים את מספר הלוג של התצפיות מול סטיית התקן המשוערת, ולראות שהקשר הוא ליניארי בקירוב.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

png

השוואת lme4 ב R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

הטבלה הבאה מסכמת את התוצאות.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

טבלה זו מציינת את VI התוצאות הן בתוך ~ 10% של lme4 של. זה קצת מפתיע שכן:

  • lme4 מבוסס על השיטה לפלס (לא VI),
  • לא נעשה מאמץ בקולאב הזה להתכנס בפועל,
  • נעשה מאמץ מינימלי לכוונון היפרפרמטרים,
  • לא נעשה מאמץ להסדיר או לעבד מראש את הנתונים (למשל, תכונות מרכז וכו').

סיכום

בקולאב זה תיארנו מודלים של אפקטים מעורבים ליניאריים כלליים והראנו כיצד להשתמש בהסקת וריאציות כדי להתאים אותם באמצעות הסתברות TensorFlow. למרות שלבעיית הצעצוע היו רק כמה מאות דוגמאות אימון, הטכניקות המשמשות כאן זהות למה שצריך בקנה מידה.