برازش مدلهای اثرات ترکیبی خطی تعمیم یافته با استفاده از استنباط تنوع

مشاهده در TensorFlow.org در Google Colab اجرا شود مشاهده منبع در GitHub دانلود دفترچه یادداشت

نصب

نصب

خلاصه

در این colab ما نشان می‌دهیم که چگونه یک مدل اثرات مختلط خطی تعمیم‌یافته را با استفاده از استنتاج متغیر در TensorFlow Probability برازش دهیم.

خانواده مدل

خطی تعمیم مدل های مخلوط اثر (glmM صورت) مشابه هستند تعمیم مدل های خطی (GLM) به جز که آنها سر و صدا خاص نمونه به پاسخ خطی پیش بینی ترکیب. این تا حدی مفید است زیرا به ویژگی‌هایی که به ندرت دیده می‌شوند اجازه می‌دهد اطلاعات را با ویژگی‌های رایج‌تر به اشتراک بگذارند.

به عنوان یک فرآیند تولیدی، یک مدل اثرات مختلط خطی تعمیم یافته (GLMM) با موارد زیر مشخص می شود:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

جایی که:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

به عبارت دیگر، این می گوید که هر دسته از هر گروه با یک نمونه، در ارتباط \(\beta_{rc}\)، از یک نرمال چند متغیره. اگر چه \(\beta_{rc}\) تساوی همیشه مستقل، آنها را تنها indentically برای یک گروه توزیع \(r\): اطلاع از دقیقا یک وجود دارد \(\Sigma_r\) برای هر \(r\in\{1,\ldots,R\}\).

هنگامی که affinely با ویژگی های گروه یک نمونه (ترکیب\(z_{r,i}\))، در نتیجه سر و صدا نمونه های خاص در است \(i\)هفتم پیش بینی پاسخ خطی (که در غیر این صورت \(x_i^\top\omega\)).

هنگامی که برآورد ما \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) ما اساسا برآورد میزان سر و صدا یک گروه تصادفی اثر حمل که در غیر این صورت غرق در حال حاضر سیگنال در \(x_i^\top\omega\).

یک از گزینه های مختلف برای وجود \(\text{Distribution}\) و تابع لینک معکوس ، \(g^{-1}\). انتخاب های رایج عبارتند از:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\)،
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\)، و،
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

برای استفاده از امکانات بیشتر، نگاه کنید به tfp.glm ماژول.

استنتاج متغیر

متاسفانه، پیدا کردن حداکثر تخمین احتمال پارامترهای \(\beta,\{\Sigma_r\}_r^R\) مستلزم جدایی ناپذیر غیر تحلیلی. برای دور زدن این مشکل، ما در عوض

  1. تعریف یک خانواده پارامتری از توزیع ها ( "چگالی جانشین")، نشان داده می شود \(q_{\lambda}\) در ضمیمه.
  2. یافتن پارامترهای \(\lambda\) به طوری که \(q_{\lambda}\) است نزدیک به denstiy هدف واقعی ما است.

خانواده توزیع می شود Gaussians مستقل از ابعاد مناسب، و با "نزدیک به چگالی هدف ما"، ما معنی خواهد بود که "به حداقل رساندن اختلاف کولبک-Leibler ". به عنوان مثال نگاه : بخش 2.2 از «بررسی برای آمارشناسان تغییرات استنتاج" برای یک اشتقاق و انگیزه خوبی نوشته شده است. به طور خاص، نشان می دهد که به حداقل رساندن واگرایی KL معادل به حداقل رساندن کران پایین شواهد منفی (ELBO) است.

مشکل اسباب بازی

Gelman و همکاران (2007) "مجموعه داده رادون" یک مجموعه داده گاهی اوقات برای نشان دادن روش برای رگرسیون استفاده می شود. (به عنوان مثال، این از نزدیک مرتبط پست وبلاگ PyMC3 .) مجموعه داده رادون شامل اندازه گیری های داخلی از رادون گرفته در سراسر ایالات متحده است. رادون به طور طبیعی ocurring گاز رادیواکتیو است که سمی در غلظت های بالا.

برای نشان دادن خود، فرض کنید که ما علاقه مند به تایید این فرضیه هستیم که سطوح رادون در خانوارهای دارای زیرزمین بالاتر است. ما همچنین گمان می کنیم که غلظت رادون مربوط به نوع خاک، یعنی مسائل جغرافیایی است.

برای اینکه این مسئله را به عنوان یک مشکل ML در نظر بگیریم، سعی خواهیم کرد سطوح لگ رادون را بر اساس یک تابع خطی از طبقه ای که در آن خوانده شده است، پیش بینی کنیم. ما همچنین از شهرستان به عنوان یک اثر تصادفی استفاده می کنیم و برای این کار واریانس های ناشی از جغرافیا را در نظر می گیریم. به عبارت دیگر، ما یک با استفاده از مدل مخلوط اثر خطی تعمیم .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

ما همچنین یک بررسی سریع برای در دسترس بودن یک GPU انجام خواهیم داد:

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

دریافت مجموعه داده:

ما مجموعه داده را از مجموعه داده های TensorFlow بارگذاری می کنیم و مقداری پیش پردازش سبک انجام می دهیم.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

متخصص خانواده GLMM

در این بخش، خانواده GLMM را به کار پیش‌بینی سطوح رادون اختصاص می‌دهیم. برای انجام این کار، ابتدا مورد خاص با اثر ثابت یک GLMM را در نظر می گیریم:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

این فرض مدل است که از رادون ورود به سیستم در مشاهده \(j\) است (در انتظار) اداره شده توسط کف \(j\)هفتم خواندن بر گرفته، به علاوه برخی رهگیری ثابت است. در شبه کد، ممکن است بنویسیم

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

یک وزن به دست برای هر طبقه و یک جهانی وجود دارد intercept مدت. با نگاهی به اندازه گیری های رادون از طبقه 0 و 1، به نظر می رسد این ممکن است شروع خوبی باشد:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

png

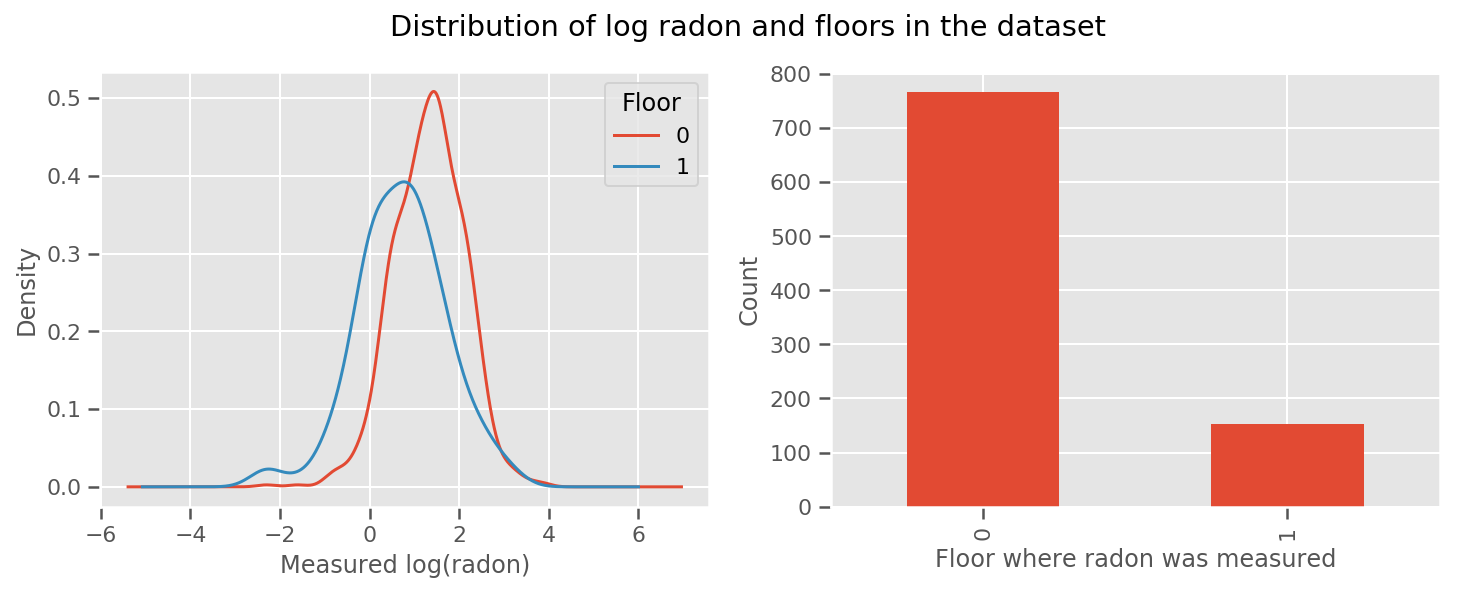
برای اینکه مدل کمی پیچیده‌تر شود، از جمله مواردی در مورد جغرافیا احتمالاً حتی بهتر است: رادون بخشی از زنجیره تجزیه اورانیوم است که ممکن است در زمین وجود داشته باشد، بنابراین به نظر می‌رسد که جغرافیا برای توضیح آن مهم باشد.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

باز هم در شبه کد داریم

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

مانند قبل به جز با وزن مخصوص شهرستان.

با توجه به مجموعه آموزشی به اندازه کافی بزرگ، این یک مدل معقول است. با این حال، با توجه به داده های ما از مینه سوتا، می بینیم که تعداد زیادی شهرستان با تعداد کمی اندازه گیری وجود دارد. به عنوان مثال، 39 شهرستان از 85 شهرستان کمتر از پنج مشاهده دارند.

این انگیزه به اشتراک گذاری قدرت آماری بین تمام مشاهدات ما را ایجاد می کند، به نحوی که با افزایش تعداد مشاهدات در هر شهرستان، به مدل فوق همگرا می شود.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

png

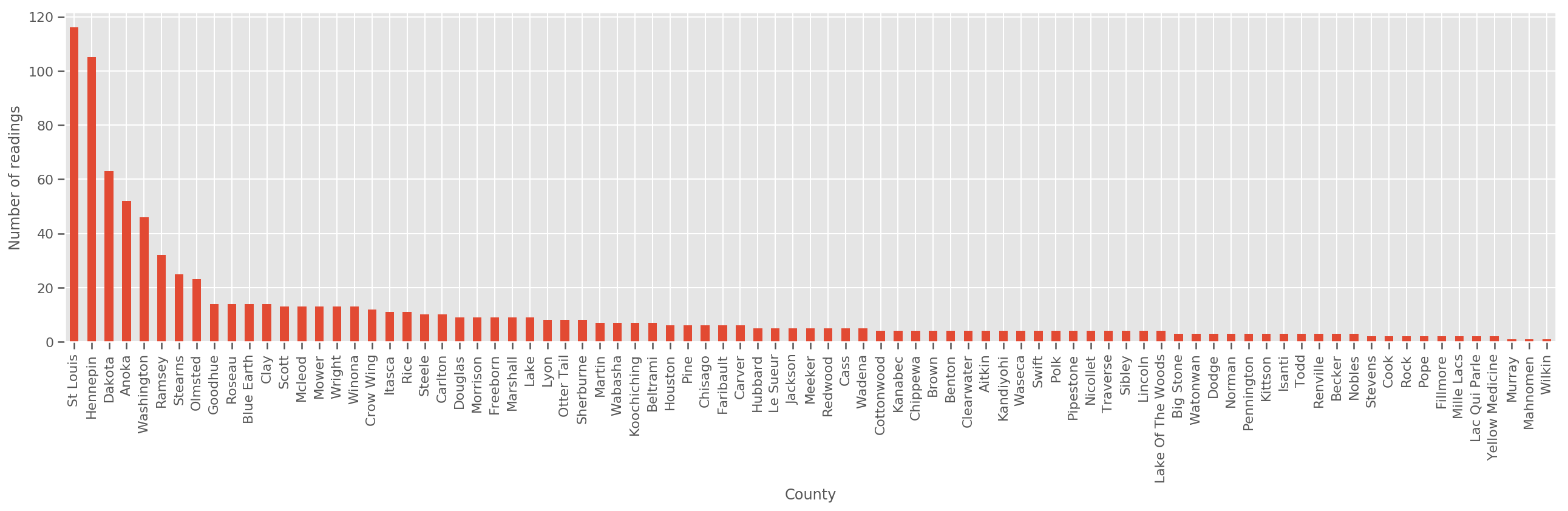
اگر ما این مدل برازش شده، county_effect بردار احتمال زیاد در نهایت حفظ نتایج را برای شهرستان که تنها چند نمونه آموزش حال، شاید Over-fitting خواهد و منجر به تعمیم ضعیف است.

GLMM یک میانه خوشحال کننده برای دو GLM فوق ارائه می دهد. شاید مناسب بودن را در نظر بگیریم

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

این مدل همان اول است، اما ما احتمال ما ثابت کرده اند که یک توزیع نرمال، و واریانس در تمام شهرستان از طریق (تک) متغیر به اشتراک بگذارید county_scale . در شبه کد،

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

ما در بر توزیع مشترک بیش از استنباط خواهد county_scale ، county_mean و random_effect با استفاده از داده های مشاهده شده است. جهانی county_scale ما اجازه می دهد برای به اشتراک گذاشتن قدرت آماری را در مناطق مختلف: کسانی که با بسیاری از مشاهدات یک ضربه در واریانس شهرستان با برخی از مشاهدات. علاوه بر این، با جمع‌آوری داده‌های بیشتر، این مدل بدون متغیر مقیاس تلفیقی به مدل همگرا می‌شود - حتی با این مجموعه داده‌ها، ما به نتایج مشابهی در مورد بیشترین شهرستان‌ها با هر مدل خواهیم رسید.

آزمایش کنید

اکنون سعی خواهیم کرد GLMM فوق را با استفاده از استنتاج متغیر در TensorFlow برازش دهیم. ابتدا داده ها را به ویژگی ها و برچسب ها تقسیم می کنیم.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

مدل را مشخص کنید

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

جانشین خلفی را مشخص کنید

ما در حال حاضر با هم یک خانواده جانشین \(q_{\lambda}\)، که در آن پارامترهای \(\lambda\) تربیت شدنی هستند. در این مورد، خانواده ما مستقل توزیع چند متغیره نرمال، یکی برای هر پارامتر، و است \(\lambda = \{(\mu_j, \sigma_j)\}\)، که در آن \(j\) شاخص چهار پارامتر.

روش استفاده می کنیم به تناسب خانواده جانشین استفاده tf.Variables . ما همچنین از tfp.util.TransformedVariable همراه با Softplus برای محدود کردن پارامترهای (تربیت شدنی) مقیاس مثبت باشد. علاوه بر این، ما اعمال می شود Softplus به کل scale_prior است، که یک پارامتر مثبت.

ما برای کمک به بهینه سازی، این متغیرهای آموزش پذیر را با کمی جیتر مقداردهی اولیه می کنیم.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

توجه داشته باشید که این سلول را می توان با جایگزین tfp.experimental.vi.build_factored_surrogate_posterior ، به عنوان در:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

نتایج

به یاد بیاورید که هدف ما این است که یک خانواده توزیع‌های پارامتری tractable را تعریف کنیم و سپس پارامترهایی را انتخاب کنیم تا توزیع قابل حملی داشته باشیم که نزدیک به توزیع هدف ما باشد.

ما در بر توزیع جانشین بالا ساخته شده است، و می توانید استفاده کنید tfp.vi.fit_surrogate_posterior ، که بهینه ساز و یک تعداد معین از مراحل قبول برای پیدا کردن پارامترهای مدل جانشین به حداقل رساندن ELBO منفی (که corresonds به حداقل رساندن اختلاف کولبک-Liebler بین جایگزین و توزیع هدف).

مقدار بازگشتی ELBO منفی در هر مرحله است، و توزیع در surrogate_posterior خواهد به روز شده اند با پارامترهای شده توسط بهینه ساز پیدا شده است.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

png

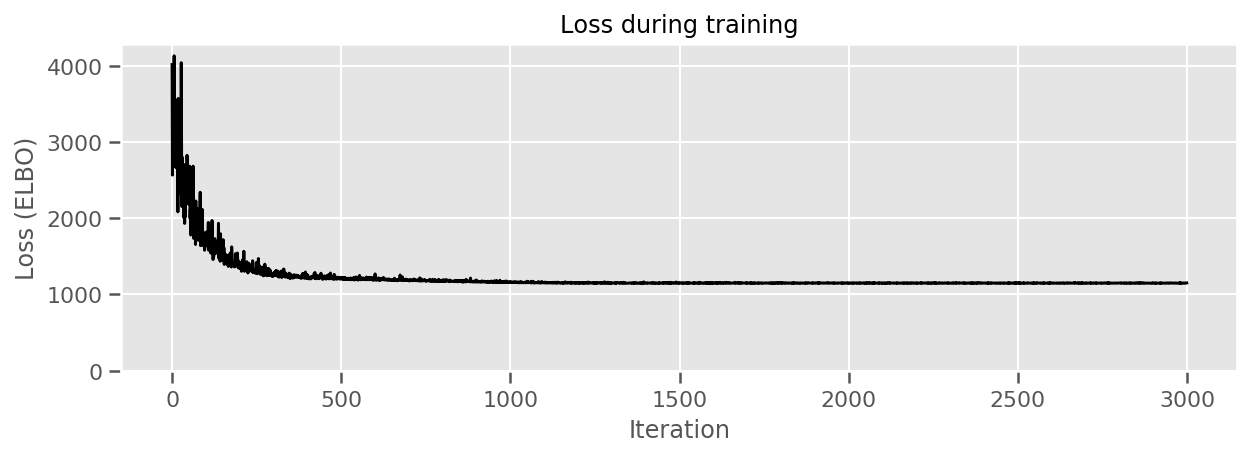
می‌توانیم اثرات میانگین تخمینی شهرستان را همراه با عدم قطعیت آن میانگین ترسیم کنیم. ما این را بر اساس تعداد مشاهدات، با بزرگترین در سمت چپ سفارش داده‌ایم. توجه داشته باشید که عدم قطعیت برای شهرستان‌هایی که مشاهدات زیادی دارند کم است، اما برای شهرستان‌هایی که فقط یک یا دو مشاهده دارند بزرگ‌تر است.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

png

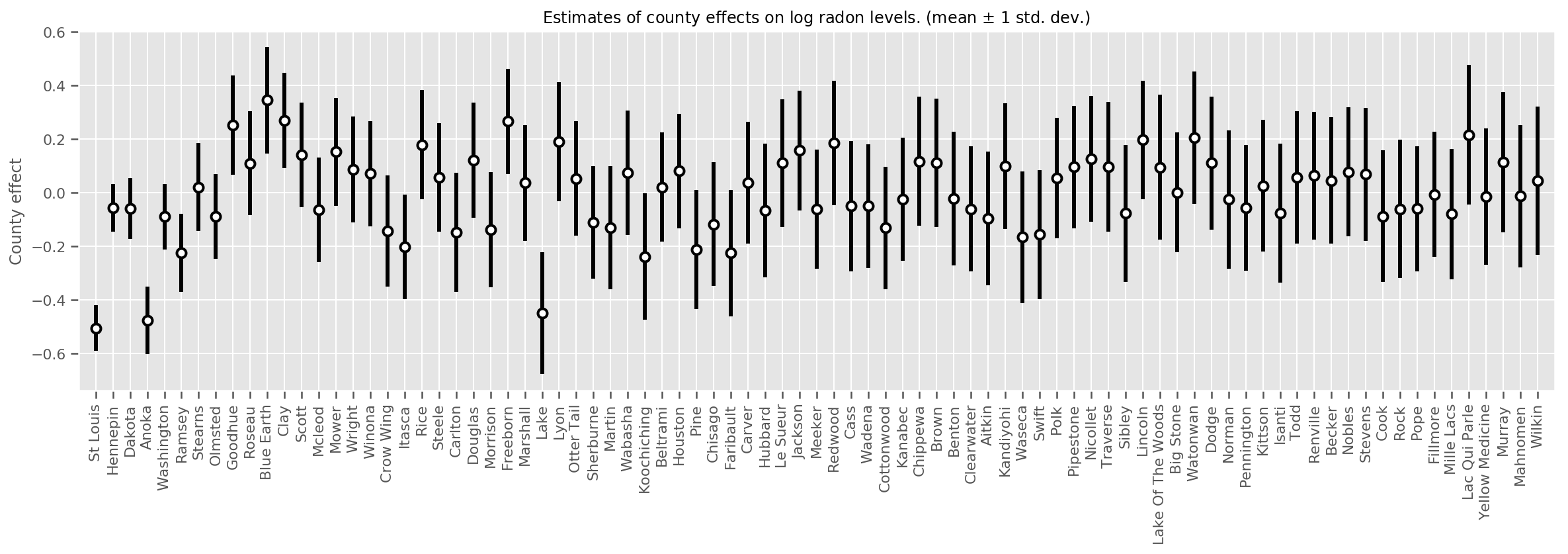
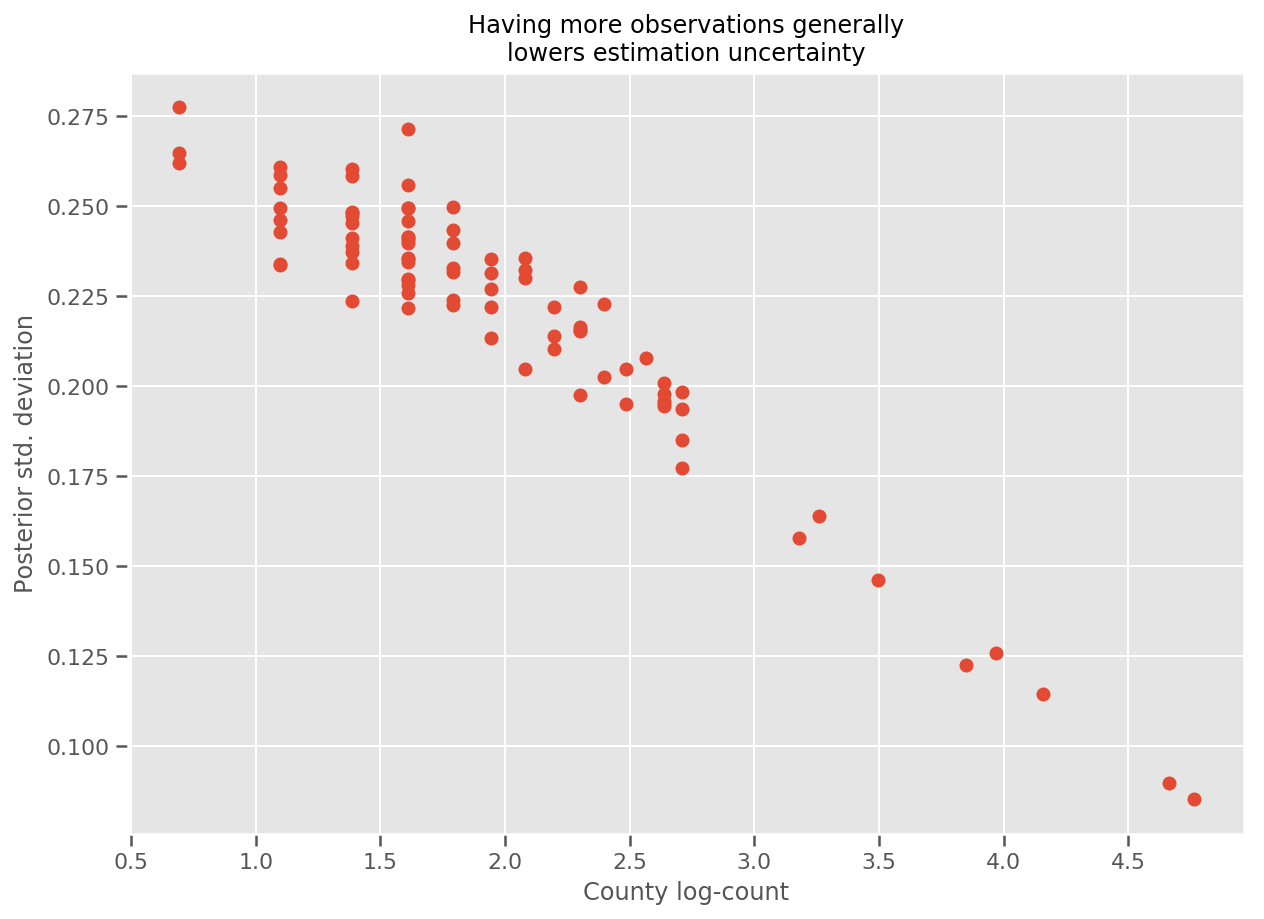
در واقع، ما می‌توانیم این را مستقیم‌تر با ترسیم تعداد لگاریتم مشاهدات در برابر انحراف استاندارد تخمین زده ببینیم و ببینیم که رابطه تقریباً خطی است.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

png

نسبت به lme4 در R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

جدول زیر نتایج را به طور خلاصه نشان می دهد.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

این جدول نشان می دهد VI نتایج در ~ 10٪ از lme4 است. این تا حدودی تعجب آور است زیرا:

  • lme4 بر اساس روش لاپلاس (نه VI)
  • هیچ تلاشی در این همکاری برای همگرایی واقعی انجام نشد،
  • حداقل تلاش برای تنظیم هایپرپارامترها انجام شد،
  • هیچ تلاشی برای منظم کردن یا پیش پردازش داده ها انجام نشده است (مثلاً ویژگی های مرکز و غیره).

نتیجه

در این colab ما مدل‌های اثرات مختلط خطی تعمیم یافته را توضیح دادیم و نحوه استفاده از استنتاج متغیر را برای برازش آنها با استفاده از TensorFlow Probability نشان دادیم. اگرچه مشکل اسباب بازی فقط چند صد نمونه آموزشی داشت، تکنیک های مورد استفاده در اینجا با آنچه در مقیاس مورد نیاز است یکسان است.