 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Instalar en pc
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
Instalar en pc
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
Abstracto
En esta colaboración, demostramos cómo ajustar un modelo lineal generalizado de efectos mixtos mediante la inferencia variacional en TensorFlow Probability.
Familia de modelos
Lineales generalizados modelos de efectos mixtos (GLMM) son similares a modelos lineales generalizados (GLM), excepto que incorporan un ruido muestra específica en la respuesta lineal predicho. Esto es útil en parte porque permite que las funciones que se ven con poca frecuencia compartan información con las funciones que se ven con más frecuencia.
Como proceso generativo, un modelo lineal generalizado de efectos mixtos (GLMM) se caracteriza por:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
donde:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
En otras palabras, este dice que cada categoría de cada grupo se asocia con una muestra, \(\beta_{rc}\), a partir de una normal multivariante. Aunque el \(\beta_{rc}\) atrae son siempre independientes, sólo se distribuyen idénticamente para un grupo \(r\): aviso hay exactamente un \(\Sigma_r\) para cada \(r\in\{1,\ldots,R\}\).
Cuando se combina affinely con las características de grupo de una muestra (\(z_{r,i}\)), el resultado es ruido específica de muestra en la \(i\)-ésimo predijo respuesta lineal (que es lo contrario \(x_i^\top\omega\)).
Cuando calculamos \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) estamos esencialmente la estimación de la cantidad de ruido de un grupo de efectos aleatorios lleva a que de otro modo ahogar la señal presente en \(x_i^\top\omega\).
Hay una variedad de opciones para el \(\text{Distribution}\) y función de enlace inversa , \(g^{-1}\). Las opciones comunes son:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), y,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
Para más posibilidades, ver el tfp.glm módulo.
Inferencia variacional
Por desgracia, la búsqueda de las estimaciones de máxima verosimilitud de los parámetros \(\beta,\{\Sigma_r\}_r^R\) implica un integrante no analítico. Para sortear este problema, en su lugar
- Definir una familia parametrizada de distribuciones (la "densidad sustituto"), denotado \(q_{\lambda}\) en el apéndice.
- Encuentra parámetros \(\lambda\) modo que \(q_{\lambda}\) está cerca de nuestra verdadera denstiy objetivo.
La familia de distribuciones gaussianas será independiente de las dimensiones adecuadas, y por "cerca de nuestro densidad objetivo", que significará "reducir al mínimo la divergencia de Kullback-Leibler ". Véase, por ejemplo, la sección 2.2 de "inferencia variacional: Una revisión de Estadísticos" para una derivación bien escrito y la motivación. En particular, muestra que minimizar la divergencia KL es equivalente a minimizar el límite inferior de evidencia negativa (ELBO).
Problema de juguete
Gelman et al. (2007) "conjunto de datos radón" es un conjunto de datos a veces utilizado para demostrar enfoques para la regresión. (Por ejemplo, esta estrechamente relacionado blog PyMC3 .) El conjunto de datos contiene radón mediciones en el interior de radón tomadas a lo largo de los Estados Unidos. Radon es, naturalmente, ocurring gas radiactivo que es tóxico en altas concentraciones.
Para nuestra demostración, supongamos que estamos interesados en validar la hipótesis de que los niveles de radón son más altos en los hogares que tienen sótano. También sospechamos que la concentración de radón está relacionada con el tipo de suelo, es decir, cuestiones geográficas.
Para enmarcar esto como un problema de ML, intentaremos predecir los niveles de log-radón en función de una función lineal del piso en el que se tomó la lectura. También usaremos el condado como un efecto aleatorio y, al hacerlo, tomaremos en cuenta las variaciones debido a la geografía. En otras palabras, vamos a utilizar un modelo de efectos mixtos lineales generalizados .
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
También haremos una comprobación rápida de la disponibilidad de una GPU:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
Obtener conjunto de datos:
Cargamos el conjunto de datos de los conjuntos de datos de TensorFlow y hacemos un preprocesamiento ligero.
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
Especializando la Familia GLMM
En esta sección, especializamos la familia GLMM a la tarea de predecir los niveles de radón. Para hacer esto, primero consideramos el caso especial de efectos fijos de un GLMM:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
Este modelo propone que el radón registro en la observación \(j\) es (en expectativa) que se rigen por el suelo el \(j\)º lectura se toma en, además de algunos de interceptación constante. En pseudocódigo, podríamos escribir
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
hay un peso aprendidas para cada piso y una universal de intercept plazo. Mirando las mediciones de radón de los pisos 0 y 1, parece que este podría ser un buen comienzo:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
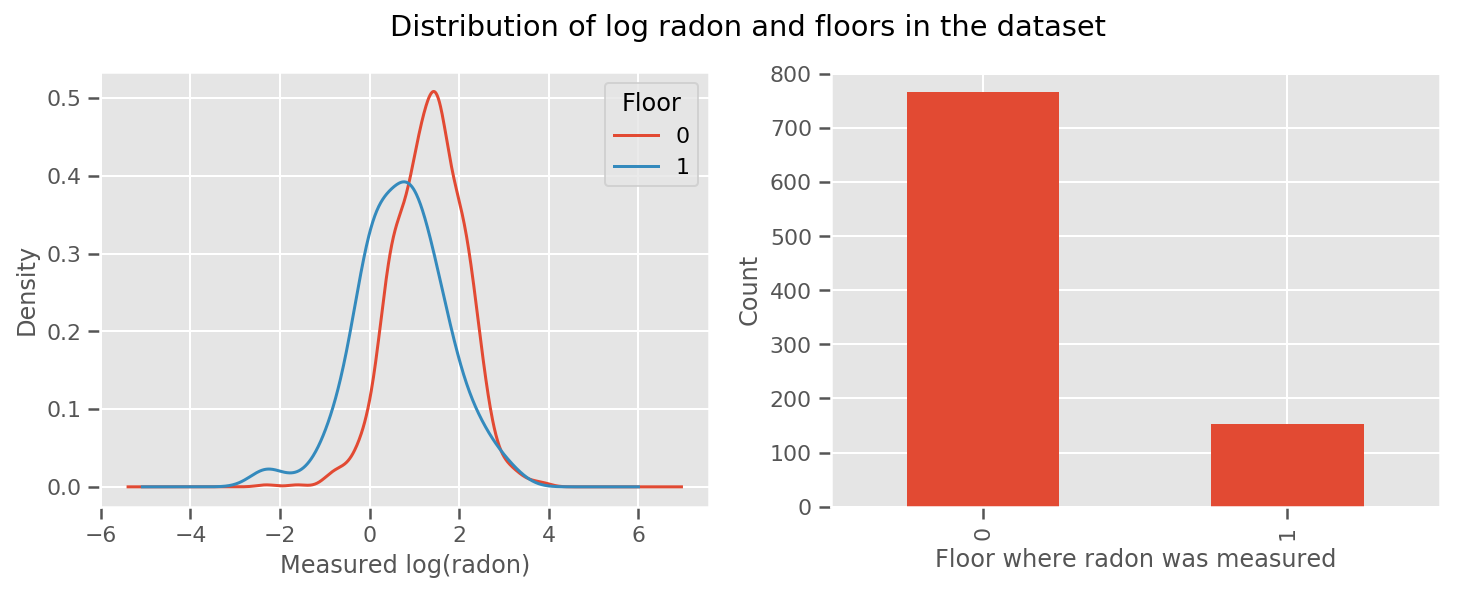
Para hacer que el modelo sea un poco más sofisticado, incluir algo sobre la geografía probablemente sea aún mejor: el radón es parte de la cadena de descomposición del uranio, que puede estar presente en el suelo, por lo que la geografía parece clave para tener en cuenta.
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
Nuevamente, en pseudocódigo, tenemos
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
lo mismo que antes excepto con un peso específico del condado.
Dado un conjunto de entrenamiento suficientemente grande, este es un modelo razonable. Sin embargo, dados nuestros datos de Minnesota, vemos que hay una gran cantidad de condados con una pequeña cantidad de mediciones. Por ejemplo, 39 de 85 condados tienen menos de cinco observaciones.
Esto motiva compartir la fuerza estadística entre todas nuestras observaciones, de manera que converge al modelo anterior a medida que aumenta el número de observaciones por condado.
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
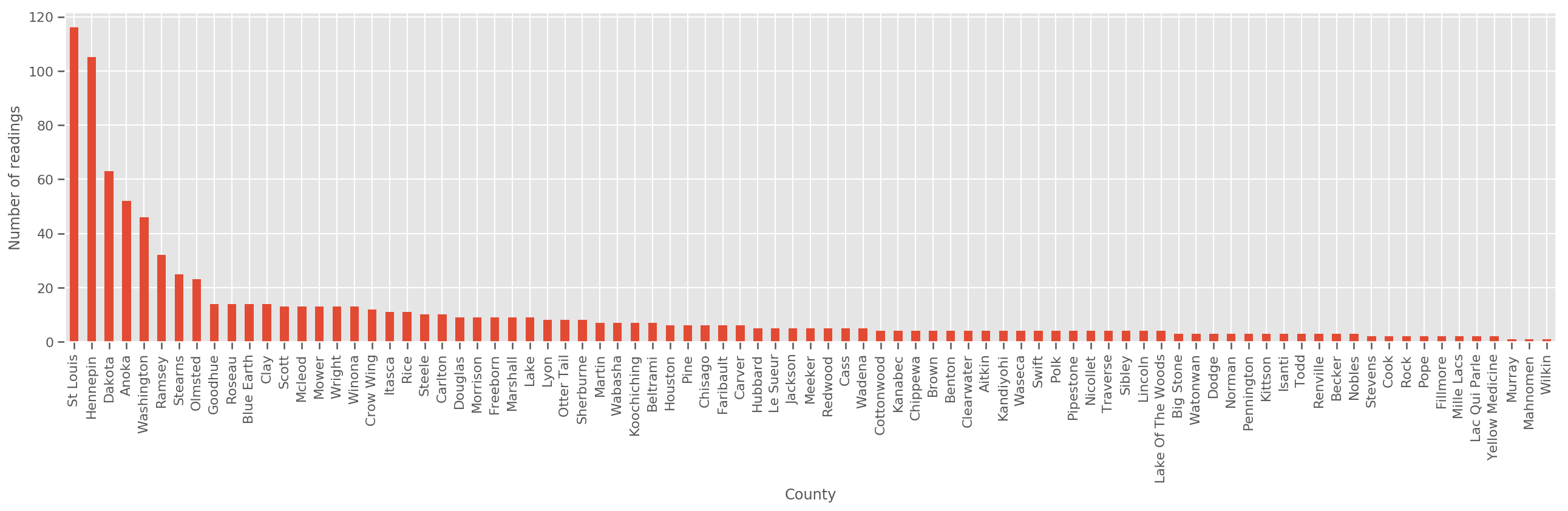
Si nos ajustamos a este modelo, el county_effect vector sería probablemente encima de la memorización de los resultados para los condados que tenían sólo unos pocos ejemplos de formación, tal vez sobreajuste y conduce a una pobre generalización.
Los GLMM ofrecen un término medio feliz para los dos GLM anteriores. Podríamos considerar apropiado
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
Este modelo es el mismo que el primero, pero hemos puesto nuestra probabilidad de ser una distribución normal, y compartirá la varianza en todos los condados a través de la (única) Variable county_scale . En pseudocódigo,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
Vamos a inferir la distribución conjunta sobre county_scale , county_mean y el random_effect usando nuestros datos observados. El mundial county_scale nos permite compartir la fuerza estadística entre los condados: los que tienen muchas observaciones proporcionar un golpe en la varianza de los condados con algunas observaciones. Además, a medida que recopilamos más datos, este modelo convergerá con el modelo sin una variable de escala agrupada; incluso con este conjunto de datos, llegaremos a conclusiones similares sobre los condados más observados con cualquiera de los modelos.
Experimentar
Ahora intentaremos ajustar el GLMM anterior mediante la inferencia variacional en TensorFlow. Primero dividiremos los datos en características y etiquetas.
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
Especificar modelo
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
Especificar sustituto posterior
Ahora ponemos juntos una familia sustituta \(q_{\lambda}\), donde los parámetros \(\lambda\) son entrenables. En este caso, nuestra familia es distribuciones normales multivariantes independientes, uno para cada parámetro, y \(\lambda = \{(\mu_j, \sigma_j)\}\), cuando \(j\) índices de los cuatro parámetros.
El método que utilice para adaptarse a las familias sustitutas usos tf.Variables . También usamos tfp.util.TransformedVariable junto con Softplus para limitar los parámetros (entrenable) escala a ser positivo. Además, aplicamos Softplus a toda la scale_prior , que es un parámetro positivo.
Inicializamos estas variables entrenables con un poco de fluctuación para ayudar en la optimización.
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
Tenga en cuenta que esta célula se puede sustituir por tfp.experimental.vi.build_factored_surrogate_posterior , como en:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
Resultados
Recuerde que nuestro objetivo es definir una familia de distribuciones parametrizadas manejable y luego seleccionar parámetros para que tengamos una distribución manejable que esté cerca de nuestra distribución objetivo.
Hemos construido la distribución sustituto anteriormente, y puede utilizar tfp.vi.fit_surrogate_posterior , que acepta un optimizador y un número dado de pasos para encontrar los parámetros para el modelo sustituto minimizando el ELBO negativo (que corresonds a reducir al mínimo la divergencia de Kullback-Liebler entre el sustituto y la distribución de destino).
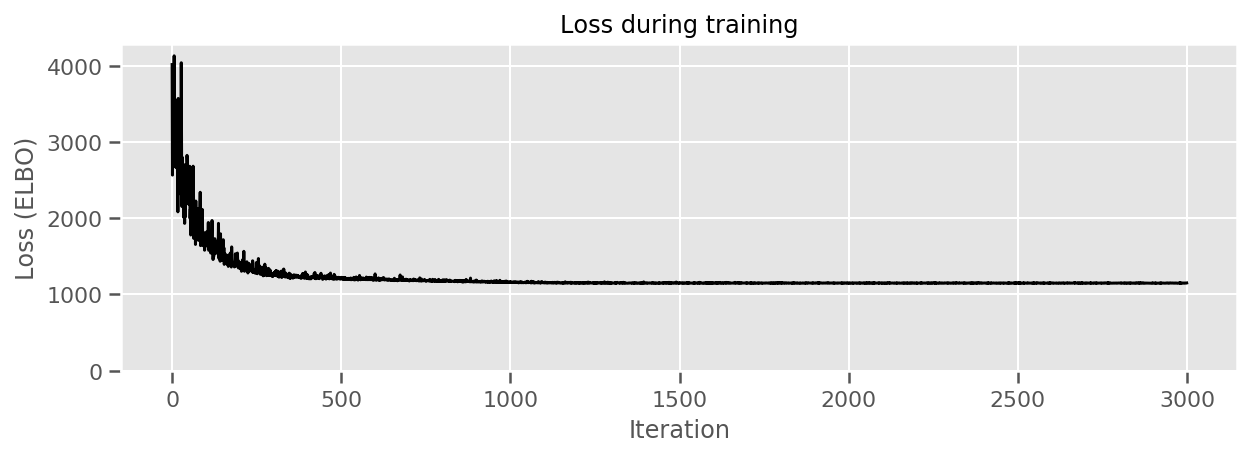
El valor de retorno es el ELBO negativa en cada paso, y las distribuciones en surrogate_posterior habrá sido actualizada con los parámetros encontrados por el optimizador.
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
Podemos graficar los efectos promedio estimados del condado, junto con la incertidumbre de esa media. Hemos ordenado esto por número de observaciones, con el más grande a la izquierda. Note que la incertidumbre es pequeña para los condados con muchas observaciones, pero es mayor para los condados que tienen solo una o dos observaciones.
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
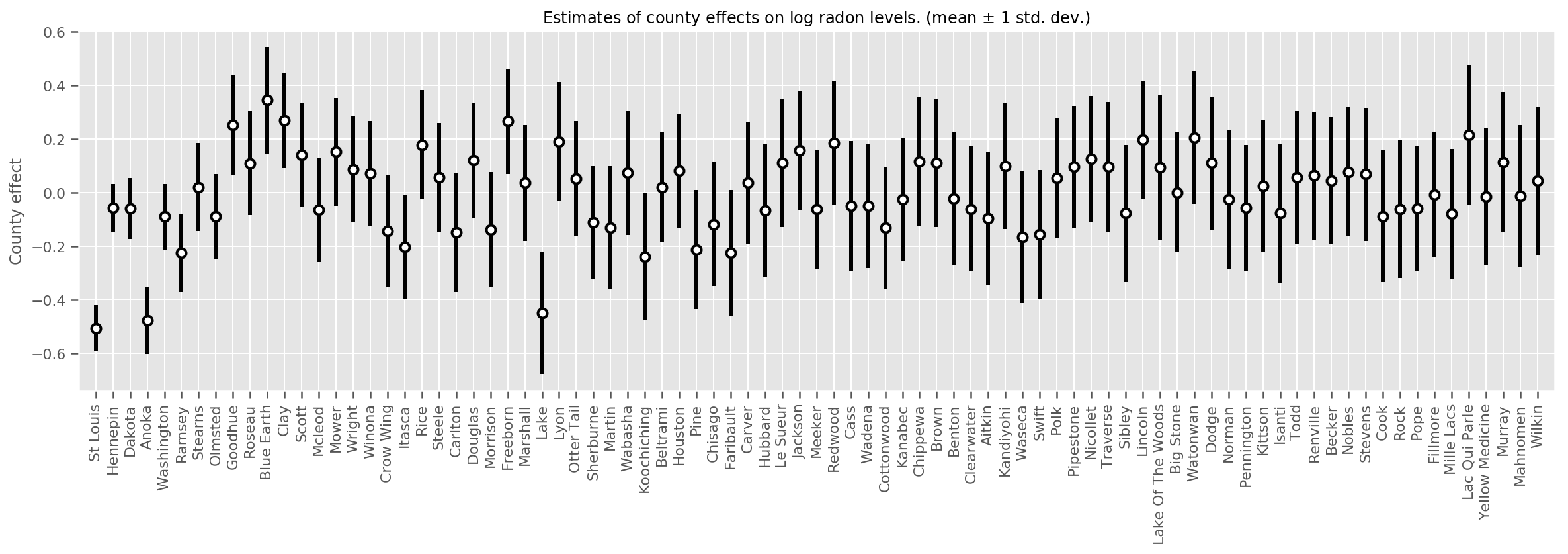
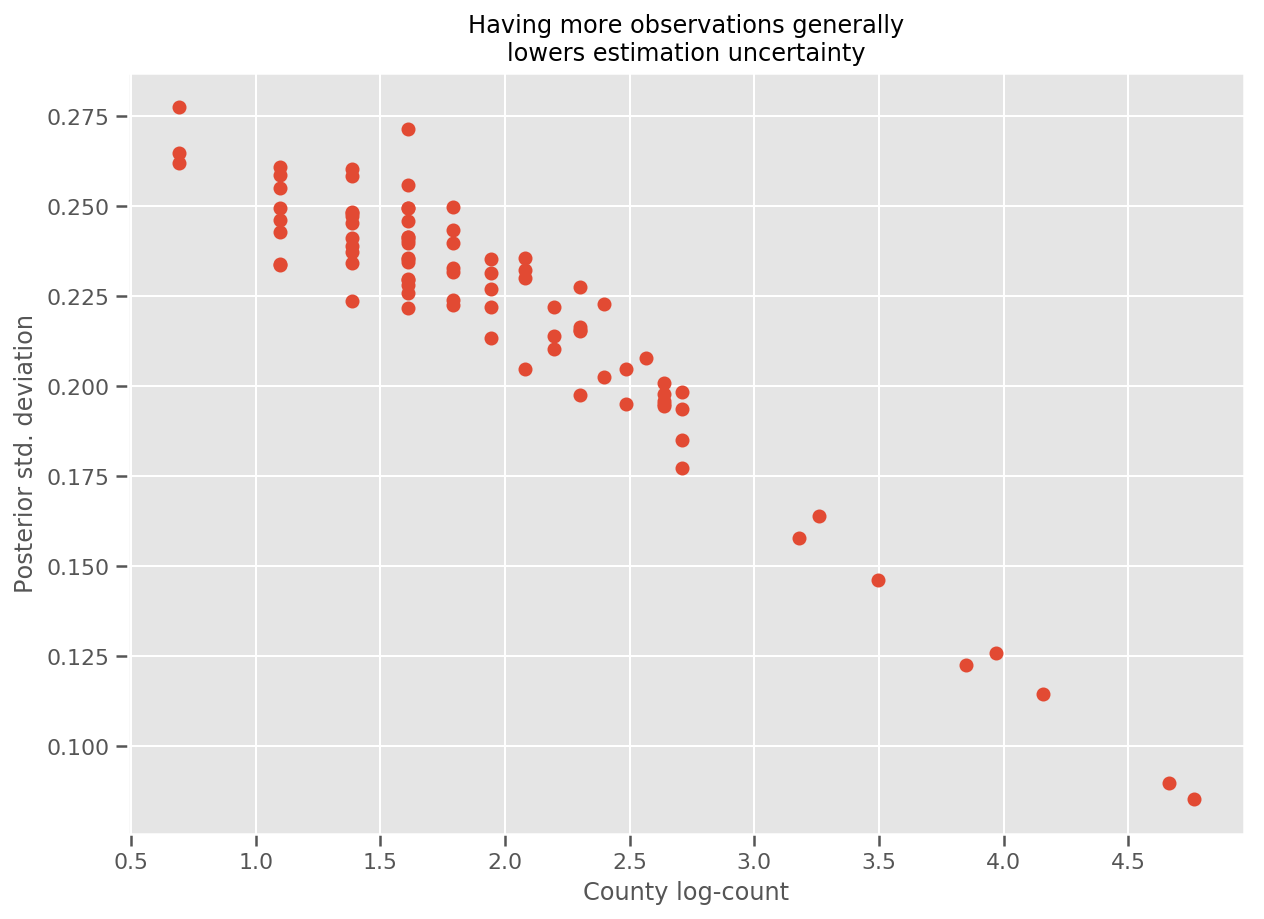
De hecho, podemos ver esto más directamente al graficar el número logarítmico de observaciones contra la desviación estándar estimada y ver que la relación es aproximadamente lineal.
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
En comparación con lme4 en I
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
La siguiente tabla resume los resultados.
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
Esta tabla indica los VI resultados están dentro de ~ 10% de lme4 's. Esto es algo sorprendente ya que:
-
lme4se basa en el método de Laplace (no VI), - no se hizo ningún esfuerzo en esta colaboración para converger realmente,
- se hizo un esfuerzo mínimo para ajustar los hiperparámetros,
- no se hizo ningún esfuerzo para regularizar o preprocesar los datos (p. ej., características del centro, etc.).
Conclusión
En esta colaboración, describimos los modelos de efectos mixtos lineales generalizados y mostramos cómo usar la inferencia variacional para ajustarlos usando la probabilidad de TensorFlow. Aunque el problema del juguete solo tenía unos pocos cientos de muestras de entrenamiento, las técnicas utilizadas aquí son idénticas a las que se necesitan a escala.
