 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
ইনস্টল করুন
TF_Installation = 'System'
if TF_Installation == 'TF Nightly':
!pip install -q --upgrade tf-nightly
print('Installation of `tf-nightly` complete.')
elif TF_Installation == 'TF Stable':
!pip install -q --upgrade tensorflow
print('Installation of `tensorflow` complete.')
elif TF_Installation == 'System':
pass
else:
raise ValueError('Selection Error: Please select a valid '
'installation option.')
ইনস্টল করুন
TFP_Installation = "System"
if TFP_Installation == "Nightly":
!pip install -q tfp-nightly
print("Installation of `tfp-nightly` complete.")
elif TFP_Installation == "Stable":
!pip install -q --upgrade tensorflow-probability
print("Installation of `tensorflow-probability` complete.")
elif TFP_Installation == "System":
pass
else:
raise ValueError("Selection Error: Please select a valid "
"installation option.")
বিমূর্ত
এই কোল্যাবে আমরা টেনসরফ্লো সম্ভাব্যতার বৈচিত্র্যগত অনুমান ব্যবহার করে একটি সাধারণ লিনিয়ার মিক্সড-ইফেক্ট মডেলকে কীভাবে ফিট করা যায় তা দেখাই।
মডেল পরিবার
মিশ্র প্রতিক্রিয়া মডেল রৈখিক সাধারণ (GLMM) একই রকম রৈখিক মডেল সাধারণ (GLM) ব্যতীত যে তারা পূর্বাভাস রৈখিক প্রতিক্রিয়া মধ্যে একটি নমুনা নির্দিষ্ট গোলমাল একত্রীভূত করে। এটি আংশিকভাবে উপযোগী কারণ এটি খুব কমই দেখা বৈশিষ্ট্যগুলিকে আরও সাধারণভাবে দেখা বৈশিষ্ট্যগুলির সাথে তথ্য ভাগ করার অনুমতি দেয়৷
একটি উৎপাদক প্রক্রিয়া হিসাবে, একটি সাধারণ রৈখিক মিশ্র প্রভাব মডেল (GLMM) দ্বারা চিহ্নিত করা হয়:
\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
কোথায়:
\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]
অন্য কথায়, এই বলছেন যে প্রতিটি দলের প্রতিটি বিভাগ একটি নমুনা, এর সাথে সংশ্লিষ্ট \(\beta_{rc}\)একটি বহুচলকীয় স্বাভাবিক থেকে। যদিও \(\beta_{rc}\) স্বপক্ষে সবসময় স্বাধীন, তারা শুধুমাত্র indentically একটি দলের জন্য বিতরণ করা হয় \(r\): নোটিশ আছে ঠিক একটি \(\Sigma_r\) প্রত্যেকের জন্য \(r\in\{1,\ldots,R\}\)।
Affinely নমুনা গ্রুপের বৈশিষ্ট্যের (সঙ্গে মিলিত যখন\(z_{r,i}\)), ফলাফলে নমুনা-নির্দিষ্ট গোলমাল \(i\)-th রৈখিক প্রতিক্রিয়া পূর্বাভাস (যা অন্যথায় হয় \(x_i^\top\omega\))।
আমরা যখন অনুমান \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) আমরা মূলত গোলমাল পরিমাণ একটি র্যান্ডম প্রতিক্রিয়া গ্রুপ বহন করে যা অন্যথায় মধ্যে সংকেত উপস্থিত আউট মজান হবে আনুমানিক হিসাব করছি \(x_i^\top\omega\)।
সেখানে বিকল্প বিভিন্ন হয় \(\text{Distribution}\) এবং বিপরীত লিংক ফাংশন , \(g^{-1}\)। সাধারণ পছন্দ হল:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), এবং,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\)।
আরো সম্ভাবনার জন্য, দেখুন tfp.glm মডিউল।
পরিবর্তনশীল অনুমান
দুর্ভাগ্যবশত, পরামিতি সর্বোচ্চ সম্ভাবনা অনুমান খোঁজার \(\beta,\{\Sigma_r\}_r^R\) অনিবার্য ফল একটি অ-বিশ্লেষণাত্মক অবিচ্ছেদ্য। এই সমস্যা প্রতিরোধ করার জন্য, আমরা পরিবর্তে
- স্থিতিমাপ কর ডিস্ট্রিবিউশন পরিবার ( "ভাড়াটে ঘনত্ব"), প্রকাশ নির্ধারণ \(q_{\lambda}\) পরিশিষ্ট।
- পরামিতি খুঁজুন \(\lambda\) যাতে \(q_{\lambda}\) আমাদের সত্য লক্ষ্য denstiy কাছাকাছি।
ডিস্ট্রিবিউশন পরিবার সঠিক মাত্রার স্বাধীন Gaussians, এবং "আমাদের লক্ষ্য ঘনত্ব পাসে" দ্বারা, আমরা মানে হবে "কমানোর হতে হবে Kullback-Leibler বিকিরণ "। উদাহরণস্বরূপ দেখুন, : "স্ট্যাটিসটিসিয়ান জন্য একটি পর্যালোচনা ভেরিয়েশনাল ইনফিরেনস" ধারা 2.2 একটি ভালো করে লেখা শিক্ষাদীক্ষা এবং প্রেরণা জন্য। বিশেষ করে, এটি দেখায় যে কেএল বিচ্যুতি হ্রাস করা নেতিবাচক প্রমাণ নিম্ন আবদ্ধ (ELBO) হ্রাস করার সমতুল্য।
খেলনা সমস্যা
Gelman এট অল। এর (2007) "রাডন ডেটা সেটটি" কখনও কখনও রিগ্রেশন জন্য পন্থা উপস্থাপন করতে ব্যবহৃত একটি ডেটাসেটের হয়। (যেমন, এই ঘনিষ্ঠভাবে সম্পর্কিত PyMC3 ব্লগ পোস্ট ।) রাডন ডেটা সেটটি রাডন এর অন্দর পরিমাপ মার্কিন যুক্তরাষ্ট্র জুড়ে নেয়া ধারণ করে। রাডন স্বাভাবিকভাবেই তেজস্ক্রিয় গ্যাস যা ocurring হয় বিষাক্ত ঘনত্ব মধ্যে।
আমাদের প্রদর্শনের জন্য, ধরুন আমরা অনুমানটি যাচাই করতে আগ্রহী যে বেসমেন্ট রয়েছে এমন পরিবারগুলিতে রেডনের মাত্রা বেশি। আমরা সন্দেহ করি রেডন ঘনত্ব মাটির প্রকারের সাথে সম্পর্কিত, অর্থাৎ, ভূগোল বিষয়ক।
এটিকে একটি ML সমস্যা হিসাবে ফ্রেম করার জন্য, আমরা যে মেঝেতে রিডিং নেওয়া হয়েছিল তার একটি রৈখিক ফাংশনের উপর ভিত্তি করে লগ-রেডন স্তরের পূর্বাভাস দেওয়ার চেষ্টা করব। আমরা কাউন্টিটিকে এলোমেলো-প্রভাব হিসাবে ব্যবহার করব এবং ভূগোলের কারণে বৈচিত্র্যের জন্য অ্যাকাউন্ট করব। অন্য কথায়, আমরা একটি ব্যবহার করব সাধারণ রৈখিক মিশ্র প্রতিক্রিয়া মডেল ।
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
আমরা একটি GPU এর উপলব্ধতার জন্য একটি দ্রুত পরীক্ষাও করব:
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
ডেটাসেট পান:
আমরা টেনসরফ্লো ডেটাসেট থেকে ডেটাসেট লোড করি এবং কিছু হালকা প্রিপ্রসেসিং করি।
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
GLMM পরিবারকে বিশেষায়িত করা
এই বিভাগে, আমরা GLMM পরিবারকে রেডন স্তরের ভবিষ্যদ্বাণী করার কাজে বিশেষায়িত করি। এটি করার জন্য, আমরা প্রথমে একটি GLMM এর ফিক্সড-ইফেক্ট বিশেষ ক্ষেত্রে বিবেচনা করি:
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
এই মডেল posits যে পর্যবেক্ষণের লগ ইন রাডন \(j\) আছে (প্রত্যাশা মধ্যে) মেঝে দ্বারা পরিচালিত \(j\)তম পাঠের ওপর নেওয়া হয়, প্লাস কিছু ধ্রুবক পথিমধ্যে। সিউডোকোডে, আমরা লিখতে পারি
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
সেখানে একটি ওজন প্রত্যেক মেঝে এবং একটি সার্বজনীন জন্য শিখেছি intercept পরিভাষা। ফ্লোর 0 এবং 1 থেকে রেডন পরিমাপ দেখে মনে হচ্ছে এটি একটি ভাল শুরু হতে পারে:
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
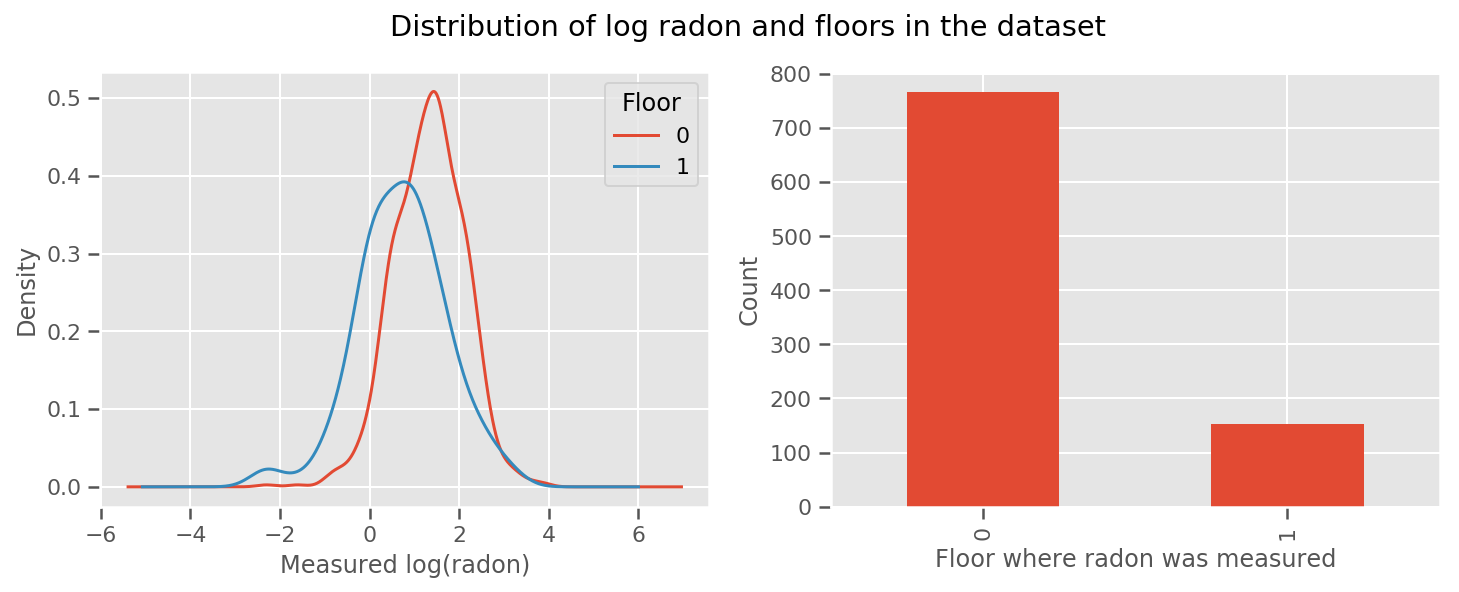
মডেলটিকে আরও পরিশীলিত করতে, ভূগোল সম্পর্কে কিছু সহ সম্ভবত আরও ভাল: রেডন ইউরেনিয়ামের ক্ষয় শৃঙ্খলের অংশ, যা মাটিতে উপস্থিত থাকতে পারে, তাই ভূগোলকে গুরুত্বপূর্ণ বলে মনে হয়।
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
আবার, pseudocode মধ্যে, আমরা আছে
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
কাউন্টি-নির্দিষ্ট ওজন ছাড়া আগের মতোই।
একটি যথেষ্ট বড় প্রশিক্ষণ সেট দেওয়া, এটি একটি যুক্তিসঙ্গত মডেল। যাইহোক, মিনেসোটা থেকে আমাদের ডেটা দেওয়া হলে, আমরা দেখতে পাচ্ছি যে সেখানে অনেক সংখ্যক কাউন্টি রয়েছে যেখানে অল্প সংখ্যক পরিমাপ রয়েছে। উদাহরণস্বরূপ, 85টি কাউন্টির মধ্যে 39টিতে পাঁচটিরও কম পর্যবেক্ষণ রয়েছে।
এটি আমাদের সমস্ত পর্যবেক্ষণের মধ্যে পরিসংখ্যানগত শক্তি ভাগাভাগি করতে অনুপ্রাণিত করে, এমনভাবে যেটি প্রতি কাউন্টিতে পর্যবেক্ষণের সংখ্যা বাড়ার সাথে সাথে উপরের মডেলের সাথে মিলিত হয়।
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
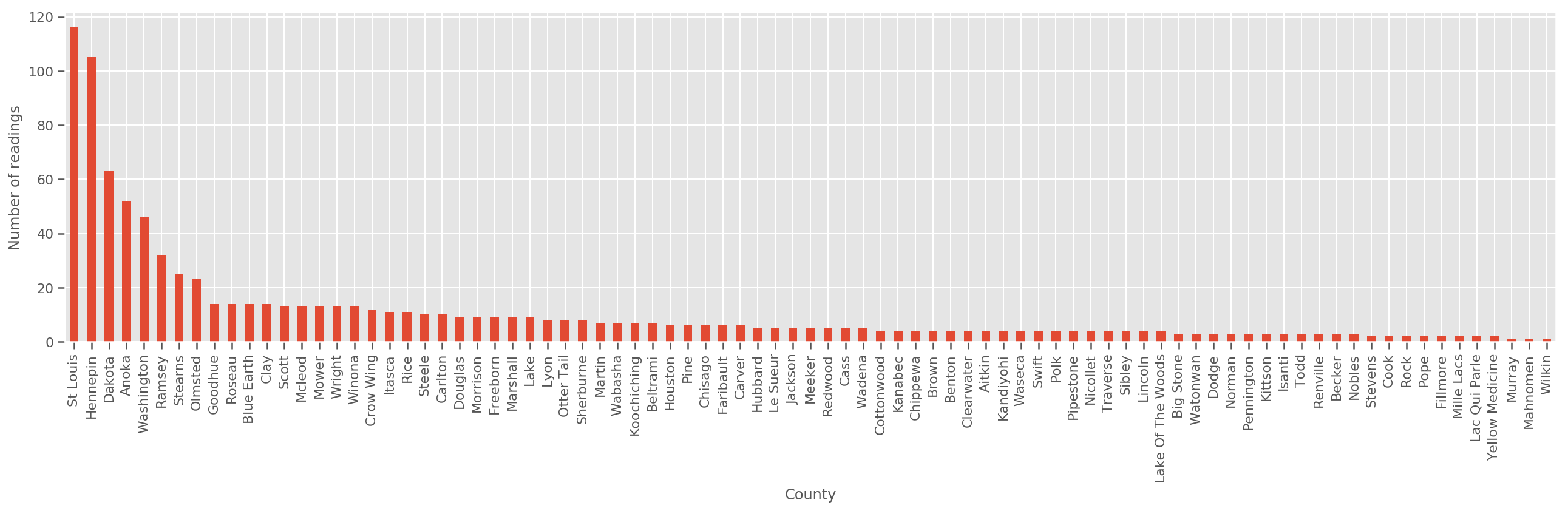
আমরা যদি এই মডেল মাপসই, county_effect ভেক্টর সম্ভবত কাউন্টিকে যা মাত্র কয়েক প্রশিক্ষণ নমুনা ছিল, সম্ভবত overfitting এবং দরিদ্র সাধারণীকরণ নেতৃস্থানীয় এর জন্য ফলাফল memorizing আপ শেষ হয়ে যাবে।
GLMM-এর অফার উপরের দুটি GLM-এর জন্য একটি সুখী মধ্যম। আমরা মানানসই বিবেচনা করতে পারে
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
এই মডেল প্রথম হিসাবে একই, কিন্তু আমরা আমাদের সম্ভাবনা সমাধান করেছেন একটি সাধারণ বন্টনের হবে, এবং (একক) পরিবর্তনশীল মাধ্যমে কাউন্টিকে জুড়ে ভ্যারিয়েন্স ভাগ করবে county_scale । সিউডোকোডে,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
আমরা ধরে যৌথ বন্টন অনুমান করবে county_scale , county_mean এবং random_effect আমাদের পর্যবেক্ষিত তথ্য ব্যবহার করে। বিশ্বব্যাপী county_scale অনেক পর্যবেক্ষণ যাদের কয়েক পর্যবেক্ষণের সঙ্গে কাউন্টিকে ভ্যারিয়েন্স এ একটি আঘাত প্রদান: আমাদের কাউন্টিকে জুড়ে পরিসংখ্যানগত শক্তি শেয়ার করতে পারবেন। তদ্ব্যতীত, আমরা আরও ডেটা সংগ্রহ করার সাথে সাথে, এই মডেলটি একটি পুল স্কেল ভেরিয়েবল ছাড়াই মডেলে একত্রিত হবে - এমনকি এই ডেটাসেটের সাথে, আমরা যেকোনও মডেলের সাথে সর্বাধিক পর্যবেক্ষণ করা কাউন্টিগুলির সম্পর্কে একই সিদ্ধান্তে উপনীত হব।
পরীক্ষা
আমরা এখন TensorFlow-এ ভ্যারিয়েশনাল ইনফারেন্স ব্যবহার করে উপরের GLMM ফিট করার চেষ্টা করব। প্রথমে আমরা ডেটাকে বৈশিষ্ট্য এবং লেবেলে বিভক্ত করব।
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
মডেল নির্দিষ্ট করুন
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
সারোগেট পোস্টেরিয়র নির্দিষ্ট করুন
আমরা এখন একসাথে একটি ভাড়াটে পরিবার করা \(q_{\lambda}\), যেখানে পরামিতি \(\lambda\) trainable হয়। এই ক্ষেত্রে, আমাদের পরিবারের স্বাধীন বহুচলকীয় স্বাভাবিক ডিস্ট্রিবিউশন, প্রতিটি প্যারামিটার জন্য এক, এবং \(\lambda = \{(\mu_j, \sigma_j)\}\), যেখানে \(j\) ইনডেক্স চার প্যারামিটার।
পদ্ধতি আমরা ভাড়াটে পরিবার ব্যবহারসমূহ মাপসই ব্যবহার tf.Variables । এছাড়া আমরা tfp.util.TransformedVariable সহ Softplus (trainable) স্কেল প্যারামিটার সীমাবদ্ধ ইতিবাচক যাবে। উপরন্তু, আমরা আবেদন করতে Softplus সমগ্র করার scale_prior , যা একটি ইতিবাচক প্যারামিটার।
অপ্টিমাইজেশানে সাহায্য করার জন্য আমরা এই প্রশিক্ষণযোগ্য ভেরিয়েবলগুলিকে কিছুটা ঝাঁকুনি দিয়ে শুরু করি।
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
নোট এই কক্ষটি দিয়ে প্রতিস্থাপিত করা যায় যে tfp.experimental.vi.build_factored_surrogate_posterior হিসেবে:
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
ফলাফল
মনে রাখবেন যে আমাদের লক্ষ্য হল একটি ট্র্যাক্টেবল প্যারামিটারাইজড ডিস্ট্রিবিউশনের পরিবারকে সংজ্ঞায়িত করা, এবং তারপরে প্যারামিটারগুলি নির্বাচন করা যাতে আমাদের লক্ষ্যবস্তু বিতরণের কাছাকাছি একটি ট্র্যাক্টেবল ডিস্ট্রিবিউশন থাকে।
আমরা উপরে ভাড়াটে বন্টন নির্মাণ করেছি এবং ব্যবহার করতে পারেন tfp.vi.fit_surrogate_posterior , যা একটি অপটিমাইজার এবং ধাপের একটি প্রদত্ত সংখ্যার গ্রহণ ভাড়াটে মডেল নেতিবাচক ELBO কমানোর জন্য মাপদণ্ডগুলি (যার মধ্যে Kullback-Liebler বিকিরণ কমানোর জন্য corresonds এটি সারোগেট এবং লক্ষ্য বিতরণ)।
ফেরত মান প্রতিটি পদে পদে নেতিবাচক ELBO, এবং মধ্যে ডিস্ট্রিবিউশন surrogate_posterior পরামিতি সঙ্গে অপটিমাইজার দ্বারা পাওয়া আপডেট করা হয়েছে হবে।
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
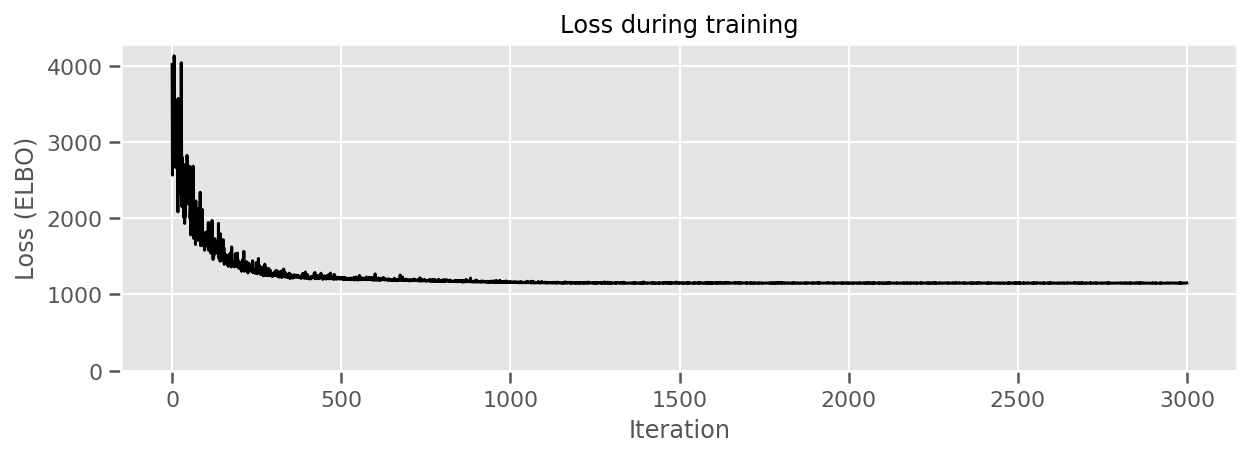
আমরা সেই গড়ের অনিশ্চয়তার সাথে আনুমানিক গড় কাউন্টি প্রভাবগুলি প্লট করতে পারি। আমরা এটিকে পর্যবেক্ষণের সংখ্যা অনুসারে অর্ডার করেছি, বাম দিকে সবচেয়ে বড়। লক্ষ্য করুন যে অনেকগুলি পর্যবেক্ষণ সহ কাউন্টির জন্য অনিশ্চয়তাটি ছোট, তবে যে কাউন্টিগুলিতে মাত্র এক বা দুটি পর্যবেক্ষণ রয়েছে তাদের জন্য এটি বড়।
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
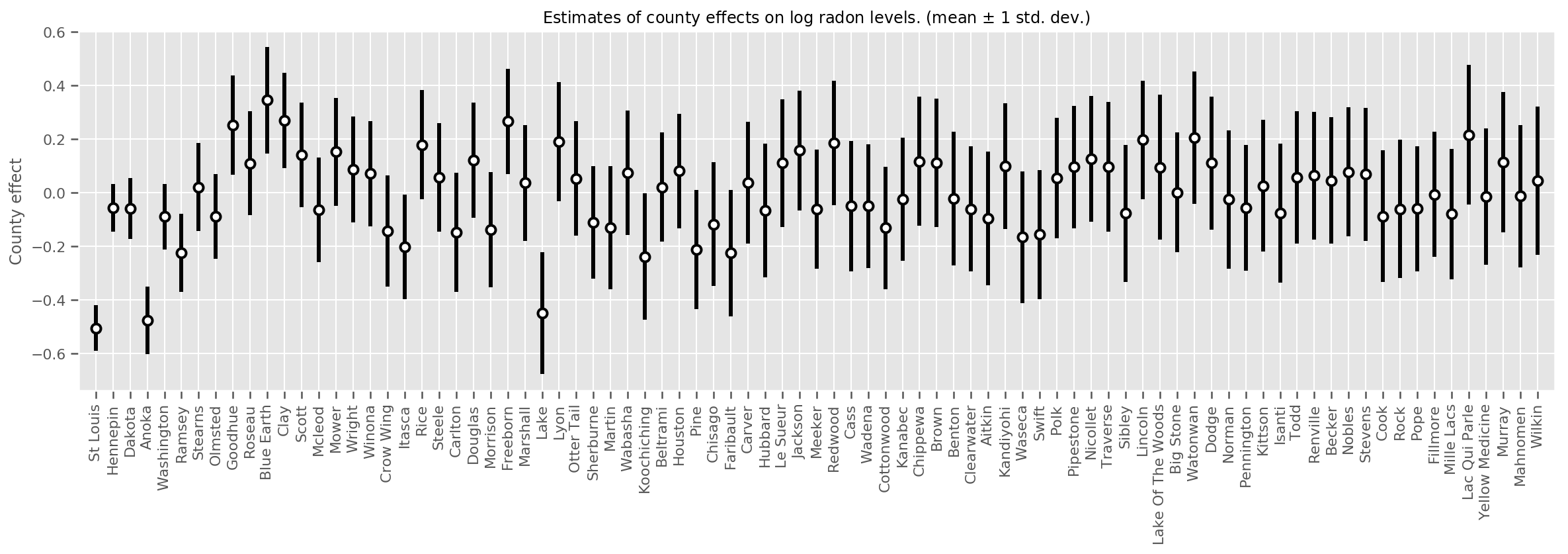
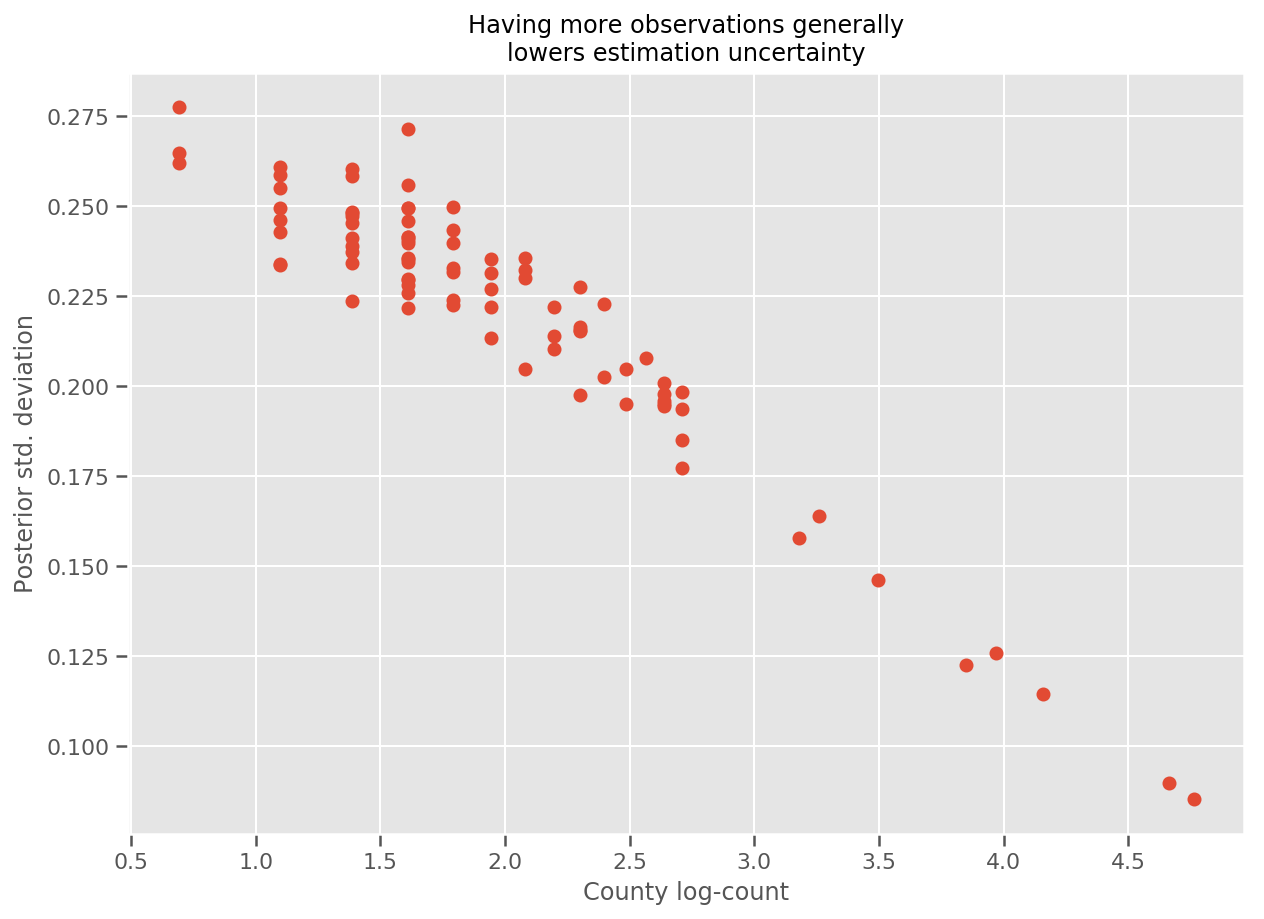
প্রকৃতপক্ষে, আমরা আনুমানিক মান বিচ্যুতির বিপরীতে পর্যবেক্ষণের লগ-সংখ্যা প্লট করে এটিকে আরও সরাসরি দেখতে পারি এবং দেখতে পারি সম্পর্কটি প্রায় রৈখিক।
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
তুলনায় lme4 দ
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
নিম্নলিখিত সারণী ফলাফলগুলিকে সংক্ষিপ্ত করে।
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
এই টেবিলের ইঙ্গিত ষষ্ঠ ফলাফল ~ মধ্যে রয়েছে 10% lme4 এর। এটি কিছুটা আশ্চর্যজনক কারণ:
-
lme4উপর ভিত্তি করে তৈরি Laplace এর পদ্ধতি (শুধুমাত্র ষষ্ঠ), - আসলে একত্রিত করার জন্য এই কোল্যাবে কোন প্রচেষ্টা করা হয়নি,
- হাইপারপ্যারামিটার টিউন করার জন্য ন্যূনতম প্রচেষ্টা করা হয়েছিল,
- ডেটা নিয়মিতকরণ বা প্রিপ্রসেস করার কোনো প্রচেষ্টা নেওয়া হয়নি (যেমন, কেন্দ্রের বৈশিষ্ট্য, ইত্যাদি)।
উপসংহার
এই কোল্যাবে আমরা সাধারণীকৃত লিনিয়ার মিক্সড-ইফেক্ট মডেলগুলি বর্ণনা করেছি এবং টেনসরফ্লো সম্ভাব্যতা ব্যবহার করে তাদের মানানসই করার জন্য পরিবর্তনগত অনুমান কীভাবে ব্যবহার করতে হয় তা দেখিয়েছি। যদিও খেলনা সমস্যাটিতে মাত্র কয়েকশ প্রশিক্ষণের নমুনা ছিল, এখানে ব্যবহৃত কৌশলগুলি স্কেলে যা প্রয়োজন তার সাথে অভিন্ন।
