تركيب نماذج التأثيرات المختلطة الخطية المعممة باستخدام الاستدلال المتغير

عرض على TensorFlow.org تشغيل في Google Colab عرض المصدر على جيثب تحميل دفتر

تثبيت

تثبيت

الملخص

في هذا colab ، نوضح كيفية ملاءمة نموذج التأثيرات المختلطة الخطي المعمم باستخدام الاستدلال المتغير في احتمالية TensorFlow.

عائلة النموذج

تعميم خطي نماذج مختلطة تأثير (GLMM) تشبه المعمم خطية نماذج (GLM) إلا أنها تتضمن عينة من ضجيج محددة في الاستجابة الخطية المتوقعة. هذا مفيد جزئيًا لأنه يسمح للميزات التي نادرًا ما يتم رؤيتها بمشاركة المعلومات مع الميزات الأكثر شيوعًا.

كعملية توليدية ، يتميز نموذج التأثيرات المختلطة الخطي المعمم (GLMM) بما يلي:

\[ \begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text{# for each random-effect group}\\ &\begin{aligned} \text{for } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{# for each category ("level") of group $r$}\\ &\begin{aligned} \beta_{rc} &\sim \text{MultivariateNormal}(\text{loc}=0_{D_r}, \text{scale}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{for } & i = 1 \ldots N: \hspace{2.45cm}\text{# for each sample}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{fixed-effects} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{random-effects} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{Distribution}(\text{mean}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]

أين:

\[ \begin{align} R &= \text{number of random-effect groups}\\ |C_r| &= \text{number of categories for group $r$}\\ N &= \text{number of training samples}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{number of fixed-effects}\\ C_r(i) &= \text{category (under group $r$) of the $i$th sample}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{number of random-effects associated with group $r$}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\\ \text{Distribution} &=\text{some distribution parameterizable solely by its mean} \end{align} \]

وبعبارة أخرى، وهذا يقول ان كل فئة من كل مجموعة ويرتبط مع عينة، \(\beta_{rc}\)، من الطبيعي متعدد المتغيرات. على الرغم من أن \(\beta_{rc}\) توجه دائما مستقلة، وأنها ليست سوى توزيع indentically لمجموعة \(r\): إشعار هناك واحد بالضبط \(\Sigma_r\) لكل \(r\in\{1,\ldots,R\}\).

عندما يقترن affinely مع ميزات المجموعة العينة من (\(z_{r,i}\))، والنتيجة هي الضوضاء عينة محددة على \(i\)-th توقع استجابة الخطية (والذي هو على خلاف ذلك \(x_i^\top\omega\)).

عندما نقدر \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) نحن تقدير أساسا كمية الضجيج يحمل مجموعة عشوائية من الآثار التي من شأنها أن يغرق إلا من إشارة موجودة في \(x_i^\top\omega\).

وهناك مجموعة متنوعة من الخيارات ل \(\text{Distribution}\) و ظيفة ارتباط عكسية ، \(g^{-1}\). الخيارات الشائعة هي:

  • \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\)،
  • \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\)، و،
  • \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

لمزيد من الاحتمالات، راجع tfp.glm حدة.

الاستدلال المتغير

للأسف، وإيجاد الحد الأقصى لتقديرات احتمال المعلمات \(\beta,\{\Sigma_r\}_r^R\) ينطوي على التكامل غير التحليلي. للتحايل على هذه المشكلة ، نحن بدلا من ذلك

  1. تعريف الأسرة معلمات من توزيعات (من "كثافة البديلة")، تدل \(q_{\lambda}\) في الملحق.
  2. البحث المعلمات \(\lambda\) بحيث \(q_{\lambda}\) بالقرب صحيح denstiy هدفنا.

سوف عائلة التوزيعات يكون Gaussians مستقلة عن الأبعاد المناسبة، و"بالقرب من كثافة هدفنا"، ونحن سوف يعني "التقليل من الاختلاف Kullback-Leibler ". انظر على سبيل المثال القسم 2.2 من "تباين الاستدلال: مراجعة لإحصاءات" لاشتقاق مكتوبة جيدا والتحفيز. على وجه الخصوص ، يُظهر أن تقليل تباعد KL يعادل تقليل الدليل السلبي الأدنى (ELBO).

مشكلة لعبة

غيلمان وآخرون. (2007) "مجموعة البيانات الرادون" هو مجموعة بيانات تستخدم في بعض الأحيان لإثبات النهج الانحدار. (على سبيل المثال، وهذا يرتبط ارتباطا وثيقا آخر PyMC3 بلوق .) مجموعة البيانات الرادون يحتوي القياسات الداخلية من الرادون اتخاذها في جميع أنحاء الولايات المتحدة. الرادون هو ocurring طبيعي الغاز المشع وهو السامة بتركيزات عالية.

من أجل العرض التوضيحي الخاص بنا ، دعنا نفترض أننا مهتمون بالتحقق من صحة الفرضية القائلة بأن مستويات الرادون أعلى في المنازل التي تحتوي على قبو. نشك أيضًا في أن تركيز الرادون مرتبط بنوع التربة ، أي مسائل الجغرافيا.

لتأطير هذا على أنه مشكلة ML ، سنحاول التنبؤ بمستويات اللوغاريتم الرادون بناءً على وظيفة خطية للأرضية التي تم أخذ القراءة عليها. سنستخدم المقاطعة أيضًا كتأثير عشوائي ، وبذلك نأخذ في الاعتبار الفروق بسبب الجغرافيا. وبعبارة أخرى، سنستخدم الخطية نموذج مختلط تأثير معمم .

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import os
from six.moves import urllib

import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds

import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

سنقوم أيضًا بإجراء فحص سريع لتوافر وحدة معالجة الرسومات (GPU):

if tf.test.gpu_device_name() != '/device:GPU:0':
  print("We'll just use the CPU for this run.")
else:
  print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))

We'll just use the CPU for this run.

الحصول على مجموعة البيانات:

نقوم بتحميل مجموعة البيانات من مجموعات بيانات TensorFlow ونقوم ببعض المعالجة المسبقة الخفيفة.

def load_and_preprocess_radon_dataset(state='MN'):
  """Load the Radon dataset from TensorFlow Datasets and preprocess it.

  Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
  to Minnesota data and preprocess to obtain the following features:
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
  df['county_code'] = df.county.cat.codes
  # Radon levels are all positive, but log levels are unconstrained
  df['log_radon'] = df['radon'].apply(np.log)

  # Drop columns we won't use and tidy the index 
  columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
  df = df[columns_to_keep].reset_index(drop=True)

  return df

df = load_and_preprocess_radon_dataset()
df.head()

متخصصون في عائلة GLMM

في هذا القسم ، نخصص عائلة GLMM لمهمة التنبؤ بمستويات الرادون. للقيام بذلك ، نعتبر أولاً الحالة الخاصة ذات التأثير الثابت لـ GLMM:

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]

هذا النموذج يفترض أن الرادون سجل في مراقبة \(j\) هو (في انتظار) التي تحكمها الطابق \(j\)يؤخذ عشر القراءة على، بالإضافة إلى بعض اعتراض ثابت. في الكود الكاذب ، قد نكتب

def estimate_log_radon(floor):
    return intercept + floor_effect[floor]

هناك وزن المستفادة من أجل كل طابق والعالمي intercept المدى. بالنظر إلى قياسات الرادون من الطابقين 0 و 1 ، يبدو أن هذه قد تكون بداية جيدة:

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')

df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");

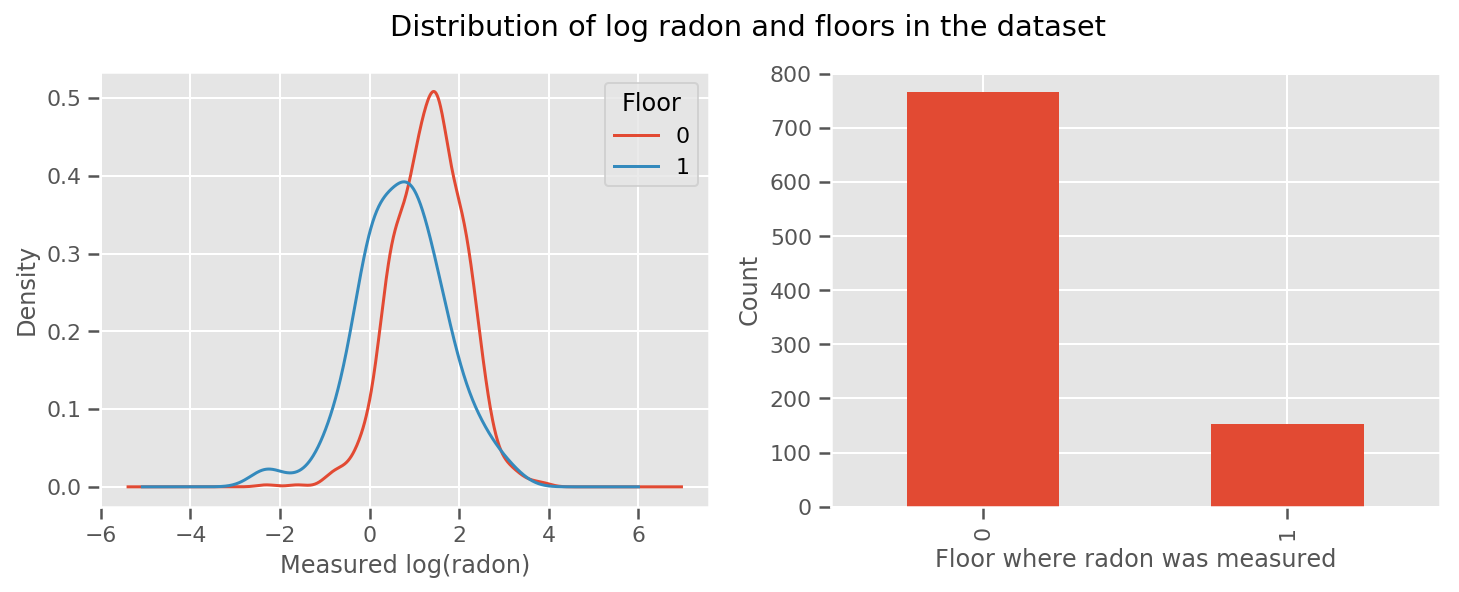
بي إن جي

لجعل النموذج أكثر تعقيدًا ، من المحتمل أن يكون تضمين شيء عن الجغرافيا أفضل: الرادون هو جزء من سلسلة اضمحلال اليورانيوم ، والتي قد تكون موجودة في الأرض ، لذلك يبدو أن الجغرافيا هي مفتاح الحساب.

\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]

مرة أخرى ، لدينا في الكود الكاذب

def estimate_log_radon(floor, county):
    return intercept + floor_effect[floor] + county_effect[county]

كما كان من قبل باستثناء الوزن المحدد للمقاطعة.

بالنظر إلى مجموعة تدريب كبيرة بما فيه الكفاية ، يعد هذا نموذجًا معقولاً. ومع ذلك ، بالنظر إلى بياناتنا من ولاية مينيسوتا ، نرى أن هناك عددًا كبيرًا من المقاطعات مع عدد صغير من القياسات. على سبيل المثال ، 39 من أصل 85 مقاطعة لديها أقل من خمس ملاحظات.

هذا يحفز مشاركة القوة الإحصائية بين جميع ملاحظاتنا ، بطريقة تتقارب مع النموذج أعلاه مع زيادة عدد الملاحظات لكل مقاطعة.

fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');

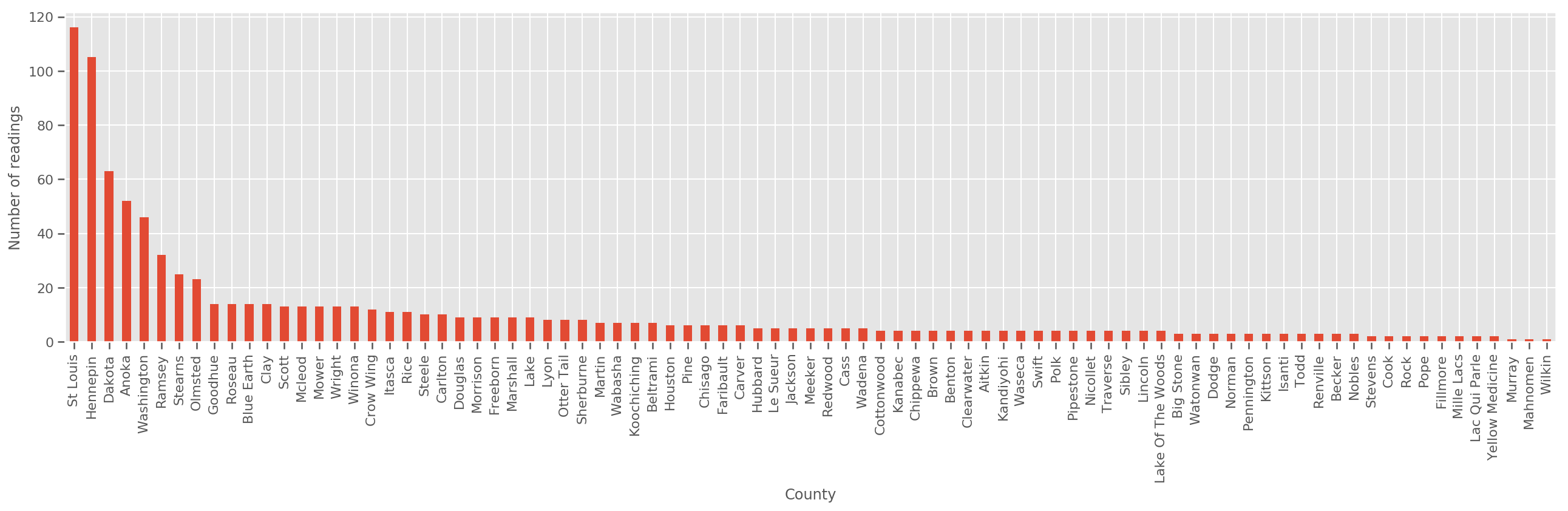
بي إن جي

إذا كان لنا أن تناسب هذا النموذج، و county_effect أن ناقلات الأرجح في نهاية المطاف حفظ نتائج المحافظات التي لم يحصل إلا على بعض العينات والتدريب، وربما overfitting ويؤدي إلى ضعف التعميم.

تقدم GLMM وسطًا سعيدًا لما ورد أعلاه GLMs. قد نفكر في التركيب

\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]

هذا النموذج هو نفس البداية، ولكن لدينا ثابت احتمال أن يكون لدينا التوزيع الطبيعي، وسوف تشارك الفرق في جميع المحافظات من خلال (واحد) متغير county_scale . في الكود الكاذب ،

def estimate_log_radon(floor, county):
    county_mean = county_effect[county]
    random_effect = np.random.normal() * county_scale + county_mean
    return intercept + floor_effect[floor] + random_effect

وسوف نستنتج توزيع مشترك على county_scale ، county_mean ، و random_effect استخدام البيانات المرصودة لدينا. العالمي county_scale يسمح لنا لتبادل القوة الإحصائية في جميع أنحاء المقاطعات: تلك مع العديد من الملاحظات توفير ضربة في تباين المقاطعات مع بعض الملاحظات. علاوة على ذلك ، عندما نجمع المزيد من البيانات ، سيتقارب هذا النموذج مع النموذج بدون متغير مقياس مجمع - حتى مع مجموعة البيانات هذه ، سوف نتوصل إلى استنتاجات مماثلة حول المقاطعات الأكثر ملاحظة مع أي من النموذجين.

تجربة

سنحاول الآن ملاءمة GLMM أعلاه باستخدام الاستدلال المتغير في TensorFlow. سنقوم أولاً بتقسيم البيانات إلى ميزات وتسميات.

features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()

حدد الطراز

def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):

  def model():
    county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
    intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
    floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
    county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
                                    scale=county_scale,
                                    name='county_prior')
    random_effect = tf.gather(county_prior, county, axis=-1)

    fixed_effect = intercept + floor_weight * floor
    linear_response = fixed_effect + random_effect
    yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
  return tfd.JointDistributionCoroutineAutoBatched(model)

joint = make_joint_distribution_coroutine(
    features.floor.values, features.county_code.values, df.county.nunique(),
    df.floor.nunique())

# Define a closure over the joint distribution 
# to condition on the observed labels.
def target_log_prob_fn(*args):
  return joint.log_prob(*args, likelihood=labels)

تحديد اللاحق البديل

وضعنا الآن معا عائلة بديل \(q_{\lambda}\)، حيث المعلمات \(\lambda\) هي قابلة للتدريب. في هذه الحالة، عائلتنا هي توزيعات مستقلة متعددة المتغيرات العادية، واحد لكل معلمة، و \(\lambda = \{(\mu_j, \sigma_j)\}\)، حيث \(j\) فهارس المعلمات الأربعة.

الطريقة التي نستخدمها لتتناسب مع الأسرة بديل الاستخدامات tf.Variables . ونحن أيضا استخدام tfp.util.TransformedVariable جنبا إلى جنب مع Softplus لتقييد المعلمات (قابلة للتدريب) على نطاق وأن تكون إيجابية. بالإضافة إلى ذلك، ونحن نطبق Softplus لكامل scale_prior ، وهي معلمة إيجابية.

نقوم بتهيئة هذه المتغيرات القابلة للتدريب مع قليل من الارتعاش للمساعدة في التحسين.

# Initialize locations and scales randomly with `tf.Variable`s and 
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
    tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
    initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
    bijector=tfb.Softplus())
n_counties = df.county.nunique()

surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
  tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())),           # scale_prior
  tfd.Normal(_init_loc(), _init_scale()),                           # intercept
  tfd.Normal(_init_loc(), _init_scale()),                           # floor_weight
  tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))])  # county_prior

علما بأن هذه الخلية يمكن استبدالها مع tfp.experimental.vi.build_factored_surrogate_posterior ، كما في:

surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
  event_shape=joint.event_shape_tensor()[:-1],
  constraining_bijectors=[tfb.Softplus(), None, None, None])

نتائج

تذكر أن هدفنا هو تحديد عائلة توزيعات ذات معلمات قابلة للتتبع ، ثم تحديد المعلمات بحيث يكون لدينا توزيع قابل للتتبع يكون قريبًا من التوزيع المستهدف.

لقد بنينا توزيع بديل أعلاه، ويمكن استخدام tfp.vi.fit_surrogate_posterior ، الذي يقبل محسن وعدد معين من الخطوات للعثور على المعلمات لنموذج بديل التقليل من ELBO سلبية (التي corresonds إلى التقليل من الاختلاف Kullback-يبلر بين البديل والتوزيع المستهدف).

قيمة الإرجاع هي ELBO سلبي في كل خطوة، والتوزيعات في surrogate_posterior سيكون قد تم تحديثها مع المعلمات وجدت من قبل محسن.

optimizer = tf.optimizers.Adam(learning_rate=1e-2)

losses = tfp.vi.fit_surrogate_posterior(
    target_log_prob_fn, 
    surrogate_posterior,
    optimizer=optimizer,
    num_steps=3000, 
    seed=42,
    sample_size=2)

(scale_prior_, 
 intercept_, 
 floor_weight_, 
 county_weights_), _ = surrogate_posterior.sample_distributions()

print('        intercept (mean): ', intercept_.mean())
print('     floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))

intercept (mean):  tf.Tensor(1.4352839, shape=(), dtype=float32)
     floor_weight (mean):  tf.Tensor(-0.6701997, shape=(), dtype=float32)
 scale_prior (approx. mean):  tf.Tensor(0.28682157, shape=(), dtype=float32)

fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
       ylabel="Loss (ELBO)",
       title="Loss during training",
       ylim=0);

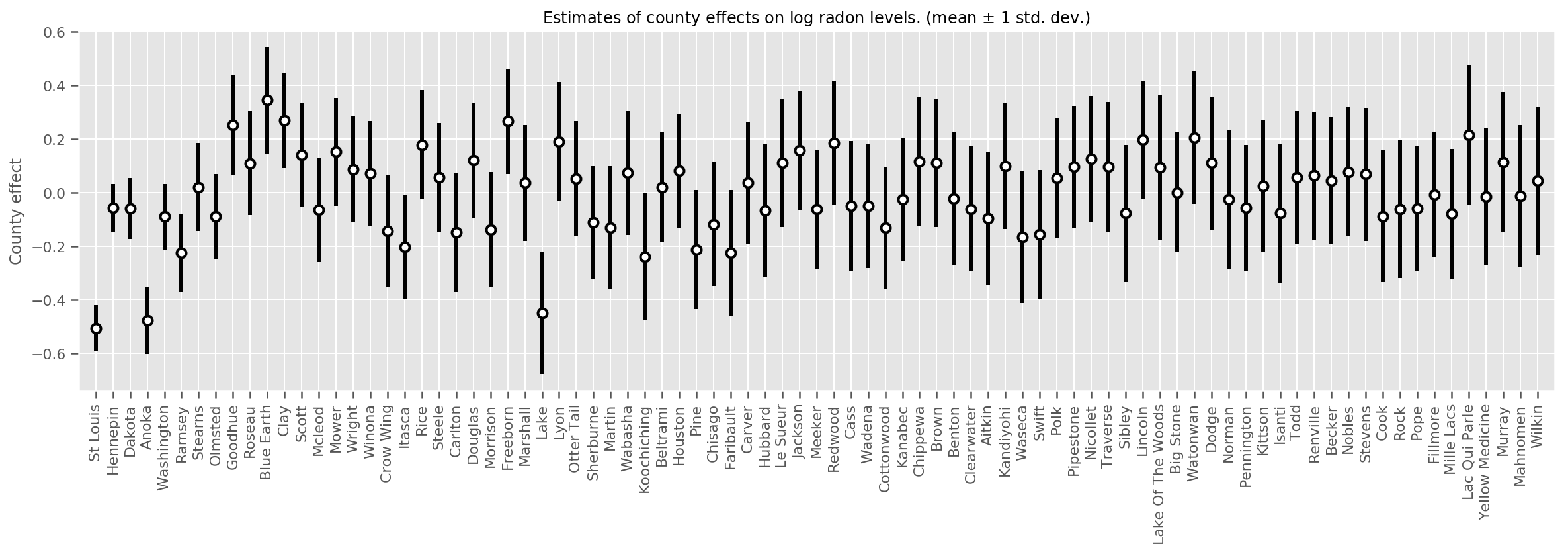
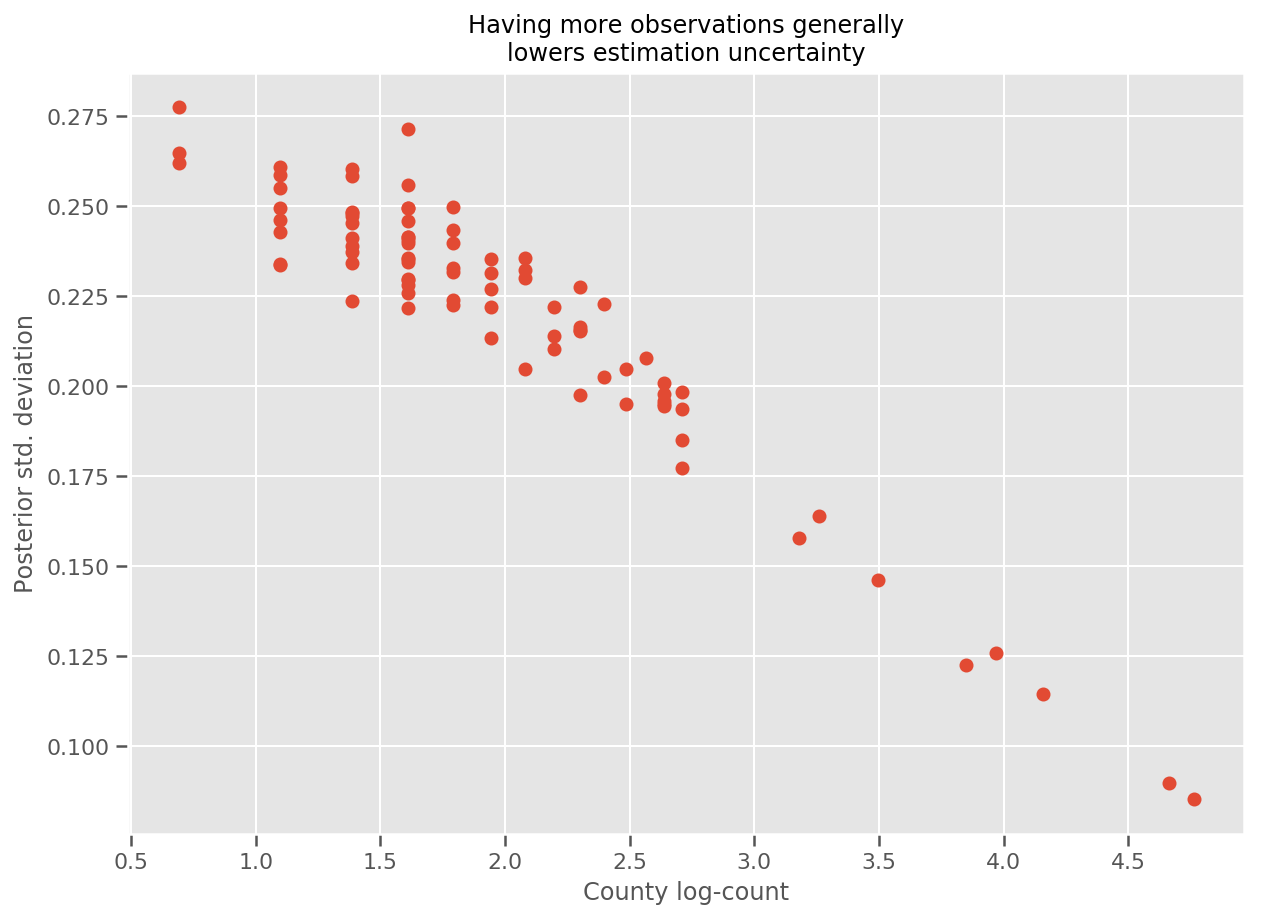
بي إن جي

يمكننا رسم مخطط متوسط ​​تأثيرات المقاطعة المقدرة ، جنبًا إلى جنب مع عدم التيقن من هذا المتوسط. لقد رتبنا هذا بعدد المشاهدات ، وأكبرها في اليسار. لاحظ أن عدم اليقين صغير بالنسبة للمقاطعات التي تحتوي على العديد من الملاحظات ، ولكنه أكبر بالنسبة للمقاطعات التي لديها ملاحظة واحدة أو اثنتين فقط.

county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
                   .agg('size')
                   .sort_values(ascending=False)
                   .reset_index(name='count'))

means = county_weights_.mean()
stds = county_weights_.stddev()

fig, ax = plt.subplots(figsize=(20, 5))

for idx, row in county_counts.iterrows():
  mid = means[row.county_code]
  std = stds[row.county_code]
  ax.vlines(idx, mid - std, mid + std, linewidth=3)
  ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)

ax.set(
    xticks=np.arange(len(county_counts)),
    xlim=(-1, len(county_counts)),
    ylabel="County effect",
    title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);

بي إن جي

في الواقع ، يمكننا رؤية هذا بشكل مباشر أكثر من خلال رسم الرقم اللوغاريتمي للملاحظات مقابل الانحراف المعياري المقدر ، ورؤية العلاقة خطية تقريبًا.

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
    ylabel='Posterior std. deviation',
    xlabel='County log-count',
    title='Having more observations generally\nlowers estimation uncertainty'
);

بي إن جي

مقارنة lme4 في R

%%shell
exit  # Trick to make this block not execute.

radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)

# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit

# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
#    Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
#  Groups   Name        Std.Dev.
#  county   (Intercept) 0.3282
#  Residual             0.7556
# Number of obs: 919, groups:  county, 85
# Fixed Effects:
# (Intercept)        floor
#       1.462       -0.693

<IPython.core.display.Javascript at 0x7f90b888e9b0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90bce1dfd0>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>
<IPython.core.display.Javascript at 0x7f90b888e780>

الجدول التالي يلخص النتائج.

print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
                             floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
                             scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
                   index=['lme4', 'vi']))

intercept   floor     scale
lme4   1.462000 -0.6930  0.328200
vi     1.435284 -0.6702  0.287251

يشير هذا الجدول السادس النتائج داخل ~ 10٪ من lme4 الصورة. هذا مثير للدهشة إلى حد ما لأن:

  • lme4 يقوم على طريقة لابلاس (لا VI)،
  • لم يُبذل أي جهد في هذا الكولاب للتلاقي فعليًا ،
  • تم بذل أقل جهد لضبط المعلمات الفائقة ،
  • لم يتم بذل أي جهد لتنظيم البيانات أو معالجتها مسبقًا (على سبيل المثال ، ميزات المركز ، إلخ).

استنتاج

وصفنا في هذا الكولاب نماذج التأثيرات المختلطة الخطية المعممة وأظهرنا كيفية استخدام الاستدلال المتغير لملاءمتها باستخدام احتمالية TensorFlow. على الرغم من أن مشكلة اللعبة لا تحتوي إلا على بضع مئات من عينات التدريب ، فإن التقنيات المستخدمة هنا مطابقة لما هو مطلوب على نطاق واسع.