{TF Probability, R, Stan}'da Lineer Karışık Etkili Regresyon

TensorFlow.org'da görüntüleyin

Google Colab'da çalıştırın

Kaynağı GitHub'da görüntüleyin

Not defterini indir

1. Giriş

Bu ortak çalışmada, popüler bir oyuncak veri kümesine doğrusal bir karma etkili regresyon modeli sığdıracağız. Biz R'ın kullanarak, bu uyum üç kez yapacak lme4 , Stan'in karışık etkiler paketi ve TensorFlow Olasılık (TFP) ilkeller. Üçünün de kabaca aynı yerleşik parametreleri ve sonsal dağılımları verdiğini göstererek sonuca varıyoruz.

Ana sonuç, TFP modelleri HLM benzeri ve yani., Diğer yazılım paketleri ile uyumlu sonuçlar ürettiğini sığdırmak için gerekli genel parçaları olmasıdır lme4 , rstanarm . Bu ortak çalışma, karşılaştırılan paketlerden herhangi birinin hesaplama verimliliğinin doğru bir yansıması değildir.

%matplotlib inline

import os
from six.moves import urllib
import numpy as np
import pandas as pd
import warnings

from matplotlib import pyplot as plt
import seaborn as sns

from IPython.core.pylabtools import figsize
figsize(11, 9)

import tensorflow.compat.v1 as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp

2 Hiyerarşik Doğrusal Model

R, Stan ve TFP tarihleri arasında bir karşılaştırma için, bir uyacak Hiyerarşik Lineer Modeli için (HLM) Radon veri kümesi popüler hale Gelman, ve arkadaşları tarafından Bayes Veri Analizi. al. (sayfa 559, ikinci baskı; sayfa 250, üçüncü baskı).

Aşağıdaki üretici modeli varsayıyoruz:

\[\begin{align*} \text{for } & c=1\ldots \text{NumCounties}:\\ & \beta_c \sim \text{Normal}\left(\text{loc}=0, \text{scale}=\sigma_C \right) \\ \text{for } & i=1\ldots \text{NumSamples}:\\ &\eta_i = \underbrace{\omega_0 + \omega_1 \text{Floor}_i}_\text{fixed effects} + \underbrace{\beta_{ \text{County}_i} \log( \text{UraniumPPM}_{\text{County}_i}))}_\text{random effects} \\ &\log(\text{Radon}_i) \sim \text{Normal}(\text{loc}=\eta_i , \text{scale}=\sigma_N) \end{align*}\]

R'ın içinde lme4 "gösterimde tilde", bu model eşdeğerdir:

log_radon ~ 1 + floor + (0 + log_uranium_ppm | county)

Biz MLE bulacaksınız \(\omega, \sigma_C, \sigma_N\) ait (kanıtlara şartlandırılmış) arka dağılım kullanılarak \(\{\beta_c\}_{c=1}^\text{NumCounties}\).

Esas olarak aynı model için rastlantısal bir kesişim ile, bakınız Ek A .

HLMs daha genel bir açıklaması için, bakınız Ek B .

3 Veri Müdahalesi

Bu bölümde elde radon veri kümesini ve bizim assumed modeli ile uyumlu hale getirmek için bazı asgari ön işlemeyi yapmak.

def load_and_preprocess_radon_dataset(state='MN'):
  """Preprocess Radon dataset as done in "Bayesian Data Analysis" book.

  We filter to Minnesota data (919 examples) and preprocess to obtain the
  following features:
  - `log_uranium_ppm`: Log of soil uranium measurements.
  - `county`: Name of county in which the measurement was taken.
  - `floor`: Floor of house (0 for basement, 1 for first floor) on which the
    measurement was taken.

  The target variable is `log_radon`, the log of the Radon measurement in the
  house.
  """
  ds = tfds.load('radon', split='train')
  radon_data = tfds.as_dataframe(ds)
  radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
  df = radon_data[radon_data.state==state.encode()].copy()

  # For any missing or invalid activity readings, we'll use a value of `0.1`.
  df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
  # Make county names look nice. 
  df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
  # Remap categories to start from 0 and end at max(category).
  county_name = sorted(df.county.unique())
  df['county'] = df.county.astype(
      pd.api.types.CategoricalDtype(categories=county_name)).cat.codes
  county_name = list(map(str.strip, county_name))

  df['log_radon'] = df['radon'].apply(np.log)
  df['log_uranium_ppm'] = df['Uppm'].apply(np.log)
  df = df[['idnum', 'log_radon', 'floor', 'county', 'log_uranium_ppm']]

  return df, county_name

radon, county_name = load_and_preprocess_radon_dataset()

# We'll use the following directory to store our preprocessed dataset.
CACHE_DIR = os.path.join(os.sep, 'tmp', 'radon')

# Save processed data. (So we can later read it in R.)
if not tf.gfile.Exists(CACHE_DIR):
  tf.gfile.MakeDirs(CACHE_DIR)
with tf.gfile.Open(os.path.join(CACHE_DIR, 'radon.csv'), 'w') as f:
  radon.to_csv(f, index=False)

3.1 Verilerinizi Bilin

Bu bölümde keşfetmek radon önerilen model makul olabilir neden daha iyi anlamak için, veri kümesini.

radon.head()

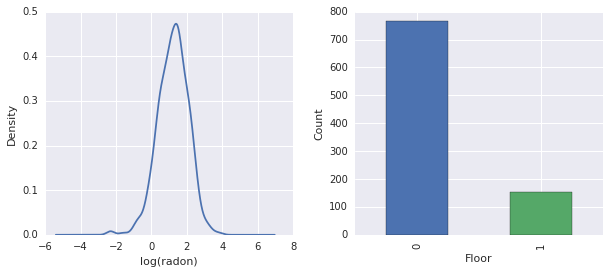
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = radon['county'].value_counts()
county_freq.plot(kind='bar', color='#436bad');
plt.xlabel('County index')
plt.ylabel('Number of radon readings')
plt.title('Number of radon readings per county', fontsize=16)
county_freq = np.array(zip(county_freq.index, county_freq.values))  # We'll use this later.

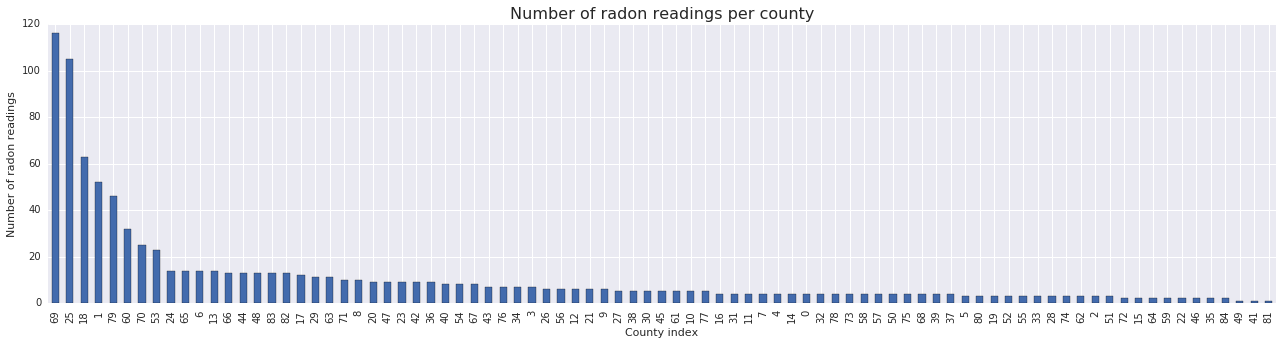
fig, ax = plt.subplots(ncols=2, figsize=[10, 4]);

radon['log_radon'].plot(kind='density', ax=ax[0]);
ax[0].set_xlabel('log(radon)')

radon['floor'].value_counts().plot(kind='bar', ax=ax[1]);
ax[1].set_xlabel('Floor');
ax[1].set_ylabel('Count');

fig.subplots_adjust(wspace=0.25)

Sonuçlar:

• 85 ilçenin uzun bir kuyruğu var. (GLMM'lerde yaygın bir durum.)
• Gerçekten de \(\log(\text{Radon})\) kısıtlamasız bir. (Yani doğrusal regresyon mantıklı olabilir.)
• Okumalar en yapılır \(0\)-inci katta; hiçbir okuma zemin üzerinde yapıldı \(1\). (Yani sabit etkilerimiz sadece iki ağırlığa sahip olacaktır.)

R'de 4 HLM

Bu bölümde R'ın kullanmak lme4 olasılık modeli yukarıda açıklanan uyacak şekilde paketi.

suppressMessages({
  library('bayesplot')
  library('data.table')
  library('dplyr')
  library('gfile')
  library('ggplot2')
  library('lattice')
  library('lme4')
  library('plyr')
  library('rstanarm')
  library('tidyverse')
  RequireInitGoogle()
})

data = read_csv(gfile::GFile('/tmp/radon/radon.csv'))

Parsed with column specification:
cols(
  log_radon = col_double(),
  floor = col_integer(),
  county = col_integer(),
  log_uranium_ppm = col_double()
)

head(data)

# A tibble: 6 x 4
  log_radon floor county log_uranium_ppm
      <dbl> <int>  <int>           <dbl>
1     0.788     1      0          -0.689
2     0.788     0      0          -0.689
3     1.06      0      0          -0.689
4     0         0      0          -0.689
5     1.13      0      1          -0.847
6     0.916     0      1          -0.847

# https://github.com/stan-dev/example-models/wiki/ARM-Models-Sorted-by-Chapter
radon.model <- lmer(log_radon ~ 1 + floor  + (0 + log_uranium_ppm | county), data = data)

summary(radon.model)

Linear mixed model fit by REML ['lmerMod']
Formula: log_radon ~ 1 + floor + (0 + log_uranium_ppm | county)
   Data: data

REML criterion at convergence: 2166.3

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.5202 -0.6064  0.0107  0.6334  3.4111 

Random effects:
 Groups   Name            Variance Std.Dev.
 county   log_uranium_ppm 0.7545   0.8686  
 Residual                 0.5776   0.7600  
Number of obs: 919, groups:  county, 85

Fixed effects:
            Estimate Std. Error t value
(Intercept)  1.47585    0.03899   37.85
floor       -0.67974    0.06963   -9.76

Correlation of Fixed Effects:
      (Intr)
floor -0.330

qqmath(ranef(radon.model, condVar=TRUE))

$county

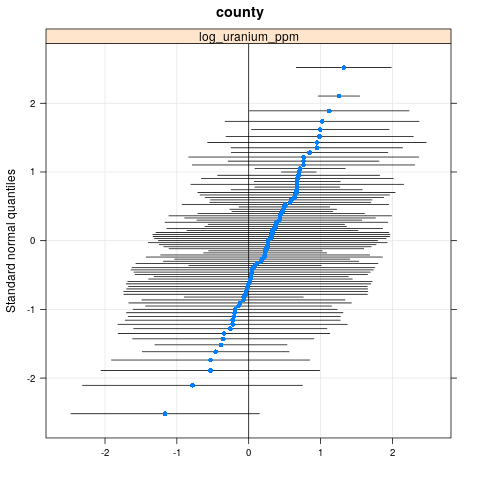
write.csv(as.data.frame(ranef(radon.model, condVar = TRUE)), '/tmp/radon/lme4_fit.csv')

Stan'de 5 HLM

Bu bölümde kullanmak rstanarm aynı formül / sözdizimi kullanılarak stan modelini tespit etmek için lme4 yukarıdaki modelde.

Aksine lme4 ve aşağıdaki TF modeli rstanarm kendilerini dağılımdan çekilmiş parametrelerle bir normal dağılımdan çekilmiş tamamen Bayes modeli yani tüm parametreler tahmin edilmektedir olduğunu.

fit <- stan_lmer(log_radon ~ 1 + floor  + (0 + log_uranium_ppm | county), data = data)

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).

Chain 1, Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1, Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1, Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1, Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1, Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1, Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1, Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1, Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1, Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1, Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1, Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1, Iteration: 2000 / 2000 [100%]  (Sampling)
 Elapsed Time: 7.73495 seconds (Warm-up)
               2.98852 seconds (Sampling)
               10.7235 seconds (Total)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).

Chain 2, Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2, Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2, Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2, Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2, Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2, Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2, Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2, Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2, Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2, Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2, Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2, Iteration: 2000 / 2000 [100%]  (Sampling)
 Elapsed Time: 7.51252 seconds (Warm-up)
               3.08653 seconds (Sampling)
               10.5991 seconds (Total)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).

Chain 3, Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3, Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3, Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3, Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3, Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3, Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3, Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3, Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3, Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3, Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3, Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3, Iteration: 2000 / 2000 [100%]  (Sampling)
 Elapsed Time: 8.14628 seconds (Warm-up)
               3.01001 seconds (Sampling)
               11.1563 seconds (Total)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).

Chain 4, Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4, Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4, Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4, Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4, Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4, Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4, Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4, Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4, Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4, Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4, Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4, Iteration: 2000 / 2000 [100%]  (Sampling)
 Elapsed Time: 7.6801 seconds (Warm-up)
               3.23663 seconds (Sampling)
               10.9167 seconds (Total)

fit

stan_lmer(formula = log_radon ~ 1 + floor + (0 + log_uranium_ppm | 
    county), data = data)

Estimates:
            Median MAD_SD
(Intercept)  1.5    0.0  
floor       -0.7    0.1  
sigma        0.8    0.0  

Error terms:
 Groups   Name            Std.Dev.
 county   log_uranium_ppm 0.87    
 Residual                 0.76    
Num. levels: county 85 

Sample avg. posterior predictive 
distribution of y (X = xbar):
         Median MAD_SD
mean_PPD 1.2    0.0   

Observations: 919  Number of unconstrained parameters: 90

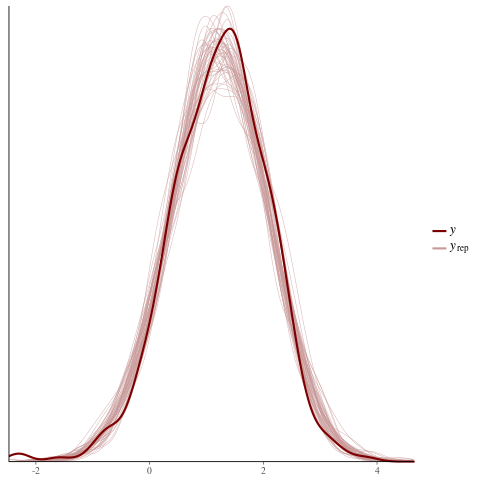
color_scheme_set("red")
ppc_dens_overlay(y = fit$y,
                 yrep = posterior_predict(fit, draws = 50))

color_scheme_set("brightblue")
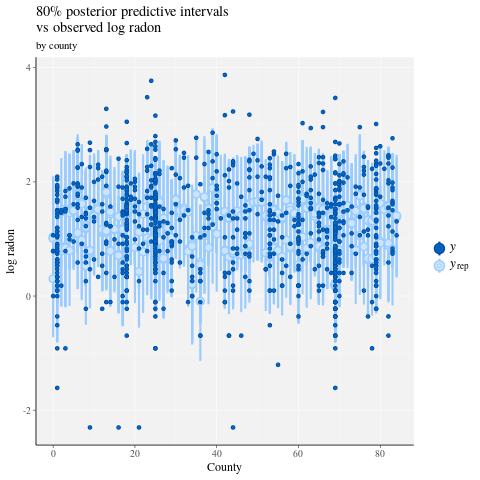
ppc_intervals(
  y = data$log_radon,
  yrep = posterior_predict(fit),
  x = data$county,
  prob = 0.8
) +
  labs(
    x = "County",
    y = "log radon",
    title = "80% posterior predictive intervals \nvs observed log radon",
    subtitle = "by county"
  ) +
  panel_bg(fill = "gray95", color = NA) +
  grid_lines(color = "white")

# Write the posterior samples (4000 for each variable) to a CSV.
write.csv(tidy(as.matrix(fit)), "/tmp/radon/stan_fit.csv")

with tf.gfile.Open('/tmp/radon/lme4_fit.csv', 'r') as f:
  lme4_fit = pd.read_csv(f, index_col=0)

lme4_fit.head()

Daha sonra görselleştirme için lme4'ten grup rastgele etkileri için nokta tahminlerini ve koşullu standart sapmaları alın.

posterior_random_weights_lme4 = np.array(lme4_fit.condval, dtype=np.float32)
lme4_prior_scale = np.array(lme4_fit.condsd, dtype=np.float32)
print(posterior_random_weights_lme4.shape, lme4_prior_scale.shape)

(85,) (85,)

lme4 tahmini ortalamaları ve standart sapmaları kullanarak ilçe ağırlıkları için örnekler çizin.

with tf.Session() as sess:
  lme4_dist = tfp.distributions.Independent(
      tfp.distributions.Normal(
          loc=posterior_random_weights_lme4,
          scale=lme4_prior_scale),
      reinterpreted_batch_ndims=1)
  posterior_random_weights_lme4_final_ = sess.run(lme4_dist.sample(4000))

posterior_random_weights_lme4_final_.shape

(4000, 85)

Ayrıca Stan uyumundan ilçe ağırlıklarının arka örneklerini alıyoruz.

with tf.gfile.Open('/tmp/radon/stan_fit.csv', 'r') as f:
  samples = pd.read_csv(f, index_col=0)

samples.head()

posterior_random_weights_cols = [
    col for col in samples.columns if 'b.log_uranium_ppm.county' in col
]
posterior_random_weights_final_stan = samples[
    posterior_random_weights_cols].values
print(posterior_random_weights_final_stan.shape)

(4000, 85)

Bunlar Stan örnek bir yakın yani TFP, doğrudan olasılık modeli belirterek bir tarzda llmer uygulamak nasıl gösterir.

TF Olasılığında 6 HLM

Bu bölümde alt düzey TensorFlow Olasılık ilkeller (kullanacaktır Distributions sıra bilinmeyen parametreleri uygun olarak Hiyerarşik Doğrusal Model belirtmek için).

# Handy snippet to reset the global graph and global session.
with warnings.catch_warnings():
  warnings.simplefilter('ignore')
  tf.reset_default_graph()
  try:
    sess.close()
  except:
    pass
  sess = tf.InteractiveSession()

6.1 Modeli Belirtin

Bu bölümde belirtmek karma etki modeli doğrusal Radon TFP ilkellerini kullanarak. Bunu yapmak için, iki TFP dağılımı üreten iki fonksiyon belirledik:

• make_weights_prior : (çarpılır rasgele ağırlıklar için çok değişkenli normal önce \(\log(\text{UraniumPPM}_{c_i})\) doğrusal tahmin compue için).
• make_log_radon_likelihood : Bir toplu Normal her gözlenen aşırı dağılımları \(\log(\text{Radon}_i)\) bağımlı değişken.

Biz TF değişkenler (yani kullanmalıdır bu dağılımların her parametrelerini uydurma olacağından tf.get_variable ). Ancak, sınırlandırılmamış optimizasyon kullanmak istediğimizden, gerekli semantiği elde etmek için gerçek değerleri sınırlamanın bir yolunu bulmalıyız, örneğin standart sapmaları temsil eden pozitifler.

inv_scale_transform = lambda y: np.log(y)  # Not using TF here.
fwd_scale_transform = tf.exp

İzleyen fonksiyon, bizim daha önceki, yapıları \(p(\beta|\sigma_C)\) burada \(\beta\) rastgele etki ağırlıkları ve belirtmektedir \(\sigma_C\) standart sapma.

Biz kullanmak tf.make_template Bu işleve ilk çağrı kullandığı TF değişkenleri ve değişkenin şimdiki değerinin yeniden sonraki tüm çağrıları başlatır sağlamak için.

def _make_weights_prior(num_counties, dtype):
  """Returns a `len(log_uranium_ppm)` batch of univariate Normal."""
  raw_prior_scale = tf.get_variable(
      name='raw_prior_scale',
      initializer=np.array(inv_scale_transform(1.), dtype=dtype))
  return tfp.distributions.Independent(
      tfp.distributions.Normal(
          loc=tf.zeros(num_counties, dtype=dtype),
          scale=fwd_scale_transform(raw_prior_scale)),
      reinterpreted_batch_ndims=1)


make_weights_prior = tf.make_template(
    name_='make_weights_prior', func_=_make_weights_prior)

İzleyen fonksiyon, bizim olabilirlik, yapıları \(p(y|x,\omega,\beta,\sigma_N)\) burada \(y,x\) göstermektedirler tepki ve kanıtlar, \(\omega,\beta\) anlamında olabildikleri de sabit ve rastgele etki ağırlıkları ve \(\sigma_N\) standart sapma.

Burada yine kullandığımız tf.make_template TF değişkenleri çağrıları arasında yeniden sağlamak için.

def _make_log_radon_likelihood(random_effect_weights, floor, county,
                               log_county_uranium_ppm, init_log_radon_stddev):
  raw_likelihood_scale = tf.get_variable(
      name='raw_likelihood_scale',
      initializer=np.array(
          inv_scale_transform(init_log_radon_stddev), dtype=dtype))
  fixed_effect_weights = tf.get_variable(
      name='fixed_effect_weights', initializer=np.array([0., 1.], dtype=dtype))
  fixed_effects = fixed_effect_weights[0] + fixed_effect_weights[1] * floor
  random_effects = tf.gather(
      random_effect_weights * log_county_uranium_ppm,
      indices=tf.to_int32(county),
      axis=-1)
  linear_predictor = fixed_effects + random_effects
  return tfp.distributions.Normal(
      loc=linear_predictor, scale=fwd_scale_transform(raw_likelihood_scale))


make_log_radon_likelihood = tf.make_template(
    name_='make_log_radon_likelihood', func_=_make_log_radon_likelihood)

Son olarak, ortak log yoğunluğunu oluşturmak için önsel ve olabilirlik üreteçlerini kullanırız.

def joint_log_prob(random_effect_weights, log_radon, floor, county,
                   log_county_uranium_ppm, dtype):
  num_counties = len(log_county_uranium_ppm)
  rv_weights = make_weights_prior(num_counties, dtype)
  rv_radon = make_log_radon_likelihood(
      random_effect_weights,
      floor,
      county,
      log_county_uranium_ppm,
      init_log_radon_stddev=radon.log_radon.values.std())
  return (rv_weights.log_prob(random_effect_weights)
          + tf.reduce_sum(rv_radon.log_prob(log_radon), axis=-1))

6.2 Eğitim (Beklenti Maksimizasyonunun Stokastik Yaklaşımı)

Doğrusal karışık etkili regresyon modelimize uyması için Beklenti Maksimizasyon algoritmasının (SAEM) stokastik bir yaklaşım versiyonunu kullanacağız. Temel fikir, beklenen eklem log yoğunluğuna (E-adım) yaklaşmak için arkadan örnekleri kullanmaktır. Daha sonra bu hesaplamayı maksimize eden parametreleri buluyoruz (M-adım). Biraz daha somut olarak, sabit nokta yinelemesi şu şekilde verilir:

\[\begin{align*} \text{E}[ \log p(x, Z | \theta) | \theta_0] &\approx \frac{1}{M} \sum_{m=1}^M \log p(x, z_m | \theta), \quad Z_m\sim p(Z | x, \theta_0) && \text{E-step}\\ &=: Q_M(\theta, \theta_0) \\ \theta_0 &= \theta_0 - \eta \left.\nabla_\theta Q_M(\theta, \theta_0)\right|_{\theta=\theta_0} && \text{M-step} \end{align*}\]

nerede \(x\) kanıt gösterir \(Z\) dışarı marjinal gereken bazı gizli değişken ve \(\theta,\theta_0\) olası parametrizasyonlari.

Daha kapsamlı bir açıklama için bkz Bernard Delyon Marc Lavielle Eric, Moulines (Ann. Devletçi., 1999) tarafından EM algoritmalarının bir stokastik yaklaşım versiyonunun Yakınsama .

E adımını hesaplamak için arkadan örnek almamız gerekir. Posteriorumuzdan örnek almak kolay olmadığı için Hamiltonian Monte Carlo (HMC) kullanıyoruz. HMC, yeni örnekler önermek için normalleştirilmemiş posterior log yoğunluğunun gradyanlarını (wrt durumu, parametreler değil) kullanan bir Monte Carlo Markov Zinciri prosedürüdür.

Normalleştirilmemiş arka log-yoğunluğunu belirtmek basittir - bu sadece, koşullandırmak istediğimiz her şeye "sabitlenmiş" ortak log-yoğunluğudur.

# Specify unnormalized posterior.

dtype = np.float32

log_county_uranium_ppm = radon[
    ['county', 'log_uranium_ppm']].drop_duplicates().values[:, 1]
log_county_uranium_ppm = log_county_uranium_ppm.astype(dtype)

def unnormalized_posterior_log_prob(random_effect_weights):
  return joint_log_prob(
      random_effect_weights=random_effect_weights,
      log_radon=dtype(radon.log_radon.values),
      floor=dtype(radon.floor.values),
      county=np.int32(radon.county.values),
      log_county_uranium_ppm=log_county_uranium_ppm,
      dtype=dtype)

Şimdi bir HMC geçiş çekirdeği oluşturarak E-adım kurulumunu tamamlıyoruz.

Notlar:

• Biz kullanmak state_stop_gradient=True aracılığıyla backpropping M-adım MCMC dan çizer önlemek için. (Bizim e-adım kasıtlı önceki en iyi bilinen tahmin edicilerin en parametre belirlenmiştir çünkü Hatırlama, İçinden backprop gerekmez.)

• Biz kullanmak tf.placeholder sonunda bizim TF grafiğini yürütmek, biz sonraki iterasyon en zincirinin değeri olarak önceki yineleme rasgele MCMC örnek beslemek böylece.

• Biz TFP en adaptif kullanmak step_size , sezgisel bir yaklaşım tfp.mcmc.hmc_step_size_update_fn .

# Set-up E-step.

step_size = tf.get_variable(
    'step_size',
    initializer=np.array(0.2, dtype=dtype),
    trainable=False)

hmc = tfp.mcmc.HamiltonianMonteCarlo(
    target_log_prob_fn=unnormalized_posterior_log_prob,
    num_leapfrog_steps=2,
    step_size=step_size,
    step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(
      num_adaptation_steps=None),
    state_gradients_are_stopped=True)

init_random_weights = tf.placeholder(dtype, shape=[len(log_county_uranium_ppm)])

posterior_random_weights, kernel_results = tfp.mcmc.sample_chain(
    num_results=3,
    num_burnin_steps=0,
    num_steps_between_results=0,
    current_state=init_random_weights,
    kernel=hmc)

Şimdi M adımını ayarlıyoruz. Bu aslında TF'de yapılabilecek bir optimizasyonla aynıdır.

# Set-up M-step.

loss = -tf.reduce_mean(kernel_results.accepted_results.target_log_prob)

global_step = tf.train.get_or_create_global_step()

learning_rate = tf.train.exponential_decay(
    learning_rate=0.1,
    global_step=global_step,
    decay_steps=2,
    decay_rate=0.99)

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss, global_step=global_step)

Bazı temizlik işleriyle bitiriyoruz. TF'ye tüm değişkenlerin başlatıldığını söylemeliyiz. Biz böylece biz de bizim TF değişkenlere kolları oluşturmak print prosedürün her tekrarda değerlerini.

# Initialize all variables.

init_op = tf.initialize_all_variables()

# Grab variable handles for diagnostic purposes.

with tf.variable_scope('make_weights_prior', reuse=True):
  prior_scale = fwd_scale_transform(tf.get_variable(
      name='raw_prior_scale', dtype=dtype))

with tf.variable_scope('make_log_radon_likelihood', reuse=True):
  likelihood_scale = fwd_scale_transform(tf.get_variable(
      name='raw_likelihood_scale', dtype=dtype))
  fixed_effect_weights = tf.get_variable(
      name='fixed_effect_weights', dtype=dtype)

6.3 Yürütme

Bu bölümde SAEM TF grafiğimizi çalıştırıyoruz. Buradaki ana hile, HMC çekirdeğinden son çekilişimizi bir sonraki yinelemeye beslemektir. Bu bizim kullanımı yoluyla elde edilir feed_dict içinde sess.run çağrısı.

init_op.run()
w_ = np.zeros([len(log_county_uranium_ppm)], dtype=dtype)

%%time
maxiter = int(1500)
num_accepted = 0
num_drawn = 0
for i in range(maxiter):
  [
      _,
      global_step_,
      loss_,
      posterior_random_weights_,
      kernel_results_,
      step_size_,
      prior_scale_,
      likelihood_scale_,
      fixed_effect_weights_,
  ] = sess.run([
      train_op,
      global_step,
      loss,
      posterior_random_weights,
      kernel_results,
      step_size,
      prior_scale,
      likelihood_scale,
      fixed_effect_weights,
  ], feed_dict={init_random_weights: w_})
  w_ = posterior_random_weights_[-1, :]
  num_accepted += kernel_results_.is_accepted.sum()
  num_drawn += kernel_results_.is_accepted.size
  acceptance_rate = num_accepted / num_drawn
  if i % 100 == 0 or i == maxiter - 1:
    print('global_step:{:>4}  loss:{: 9.3f}  acceptance:{:.4f}  '
          'step_size:{:.4f}  prior_scale:{:.4f}  likelihood_scale:{:.4f}  '
          'fixed_effect_weights:{}'.format(
              global_step_, loss_.mean(), acceptance_rate, step_size_,
              prior_scale_, likelihood_scale_, fixed_effect_weights_))

global_step:   0  loss: 1966.948  acceptance:1.0000  step_size:0.2000  prior_scale:1.0000  likelihood_scale:0.8529  fixed_effect_weights:[ 0.  1.]
global_step: 100  loss: 1165.385  acceptance:0.6205  step_size:0.2040  prior_scale:0.9568  likelihood_scale:0.7611  fixed_effect_weights:[ 1.47523439 -0.66043079]
global_step: 200  loss: 1149.851  acceptance:0.6766  step_size:0.2081  prior_scale:0.7465  likelihood_scale:0.7665  fixed_effect_weights:[ 1.48918796 -0.67058587]
global_step: 300  loss: 1163.464  acceptance:0.6811  step_size:0.2040  prior_scale:0.8445  likelihood_scale:0.7594  fixed_effect_weights:[ 1.46291411 -0.67586178]
global_step: 400  loss: 1158.846  acceptance:0.6808  step_size:0.2081  prior_scale:0.8377  likelihood_scale:0.7574  fixed_effect_weights:[ 1.47349834 -0.68823022]
global_step: 500  loss: 1154.193  acceptance:0.6766  step_size:0.1961  prior_scale:0.8546  likelihood_scale:0.7564  fixed_effect_weights:[ 1.47703862 -0.67521363]
global_step: 600  loss: 1163.903  acceptance:0.6783  step_size:0.2040  prior_scale:0.9491  likelihood_scale:0.7587  fixed_effect_weights:[ 1.48268366 -0.69667786]
global_step: 700  loss: 1163.894  acceptance:0.6767  step_size:0.1961  prior_scale:0.8644  likelihood_scale:0.7617  fixed_effect_weights:[ 1.4719094  -0.66897118]
global_step: 800  loss: 1153.689  acceptance:0.6742  step_size:0.2123  prior_scale:0.8366  likelihood_scale:0.7609  fixed_effect_weights:[ 1.47345769 -0.68343043]
global_step: 900  loss: 1155.312  acceptance:0.6718  step_size:0.2040  prior_scale:0.8633  likelihood_scale:0.7581  fixed_effect_weights:[ 1.47426116 -0.6748783 ]
global_step:1000  loss: 1151.278  acceptance:0.6690  step_size:0.2081  prior_scale:0.8737  likelihood_scale:0.7581  fixed_effect_weights:[ 1.46990883 -0.68891817]
global_step:1100  loss: 1156.858  acceptance:0.6676  step_size:0.2040  prior_scale:0.8716  likelihood_scale:0.7584  fixed_effect_weights:[ 1.47386014 -0.6796245 ]
global_step:1200  loss: 1166.247  acceptance:0.6653  step_size:0.2000  prior_scale:0.8748  likelihood_scale:0.7588  fixed_effect_weights:[ 1.47389269 -0.67626756]
global_step:1300  loss: 1165.263  acceptance:0.6636  step_size:0.2040  prior_scale:0.8771  likelihood_scale:0.7581  fixed_effect_weights:[ 1.47612262 -0.67752427]
global_step:1400  loss: 1158.108  acceptance:0.6640  step_size:0.2040  prior_scale:0.8748  likelihood_scale:0.7587  fixed_effect_weights:[ 1.47534692 -0.6789524 ]
global_step:1499  loss: 1161.030  acceptance:0.6638  step_size:0.1941  prior_scale:0.8738  likelihood_scale:0.7589  fixed_effect_weights:[ 1.47624075 -0.67875224]
CPU times: user 1min 16s, sys: 17.6 s, total: 1min 33s
Wall time: 27.9 s

Yaklaşık 1500 adımdan sonra, parametre tahminlerimiz stabilize oldu.

6.4 Sonuçlar

Artık parametreleri uydurduğumuza göre, çok sayıda sonsal örnek oluşturalım ve sonuçları inceleyelim.

%%time
posterior_random_weights_final, kernel_results_final = tfp.mcmc.sample_chain(
    num_results=int(15e3),
    num_burnin_steps=int(1e3),
    current_state=init_random_weights,
    kernel=tfp.mcmc.HamiltonianMonteCarlo(
      target_log_prob_fn=unnormalized_posterior_log_prob,
      num_leapfrog_steps=2,
      step_size=step_size))

[
    posterior_random_weights_final_,
    kernel_results_final_,
] = sess.run([
    posterior_random_weights_final,
    kernel_results_final,
], feed_dict={init_random_weights: w_})

CPU times: user 1min 42s, sys: 26.6 s, total: 2min 8s
Wall time: 35.1 s

print('prior_scale: ', prior_scale_)
print('likelihood_scale: ', likelihood_scale_)
print('fixed_effect_weights: ', fixed_effect_weights_)
print('acceptance rate final: ', kernel_results_final_.is_accepted.mean())

prior_scale:  0.873799
likelihood_scale:  0.758913
fixed_effect_weights:  [ 1.47624075 -0.67875224]
acceptance rate final:  0.7448

Şimdi, bir kutu ve bıyık diyagramı oluşturmak \(\beta_c \log(\text{UraniumPPM}_c)\) rastgele etki. Rastgele etkileri ilçe sıklığını azaltarak sıralayacağız.

x = posterior_random_weights_final_ * log_county_uranium_ppm
I = county_freq[:, 0]
x = x[:, I]
cols = np.array(county_name)[I]
pw = pd.DataFrame(x)
pw.columns = cols

fig, ax = plt.subplots(figsize=(25, 4))
ax = pw.boxplot(rot=80, vert=True);

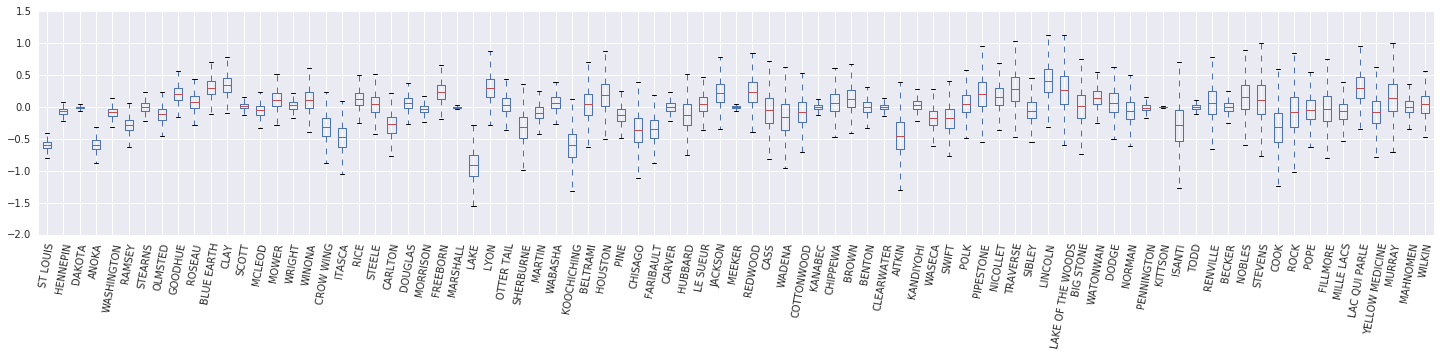
Bu kutu ve visker Diyagramımızdan, il düzeyinde varyansı gözlemlemek \(\log(\text{UraniumPPM})\) ilçesinde rasgele etki artışları daha az veri kümesi ile temsil edilir. Sezgisel olarak bu mantıklı - eğer daha az kanıtımız varsa, belirli bir ilçenin etkisi hakkında daha az emin olmalıyız.

7 Yan Yana Karşılaştırma

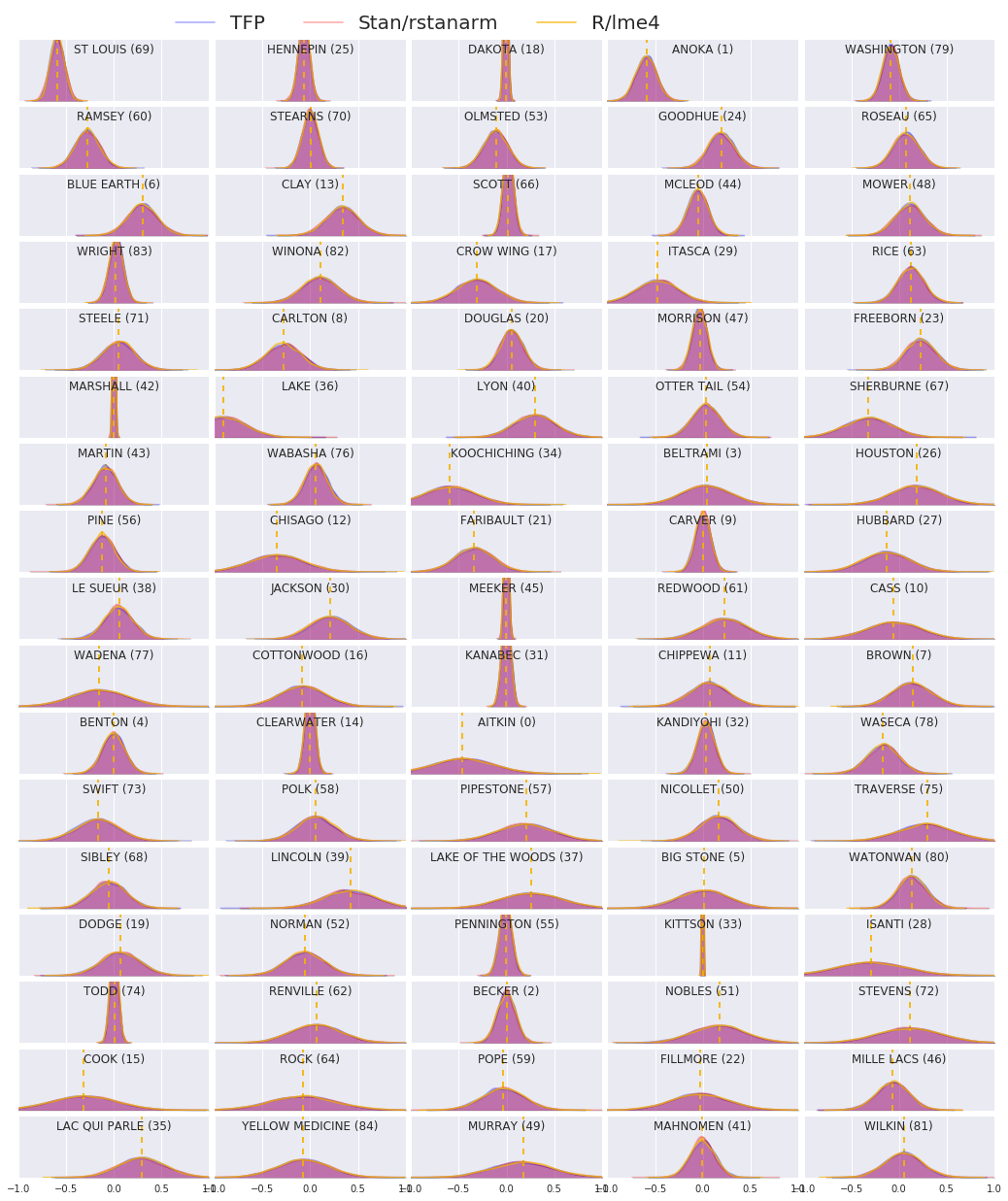
Şimdi üç prosedürün sonuçlarını karşılaştırıyoruz. Bunu yapmak için, Stan ve TFP tarafından oluşturulan sonsal örneklerin parametrik olmayan tahminlerini hesaplayacağız. Biz de R'ın tarafından üretilen tahminleri parameteric (yaklaşık) karşı karşılaştırır lme4 paketinin.

Aşağıdaki grafik, Minnesota'daki her ilçe için her ağırlığın arkadaki dağılımını göstermektedir. Biz Stan (kırmızı), (mavi) TFP ve R'ın için sonuçları gösterir lme4 (turuncu). Stan ve TFP'den elde edilen sonuçları gölgeliyoruz, bu nedenle ikisi aynı fikirde olduğunda mor görmeyi bekliyoruz. Basit olması için, sonuçları R'den gölgelemiyoruz. Her alt grafik tek bir ilçeyi temsil eder ve raster tarama düzeninde azalan sıklıkta sıralanır (yani, soldan sağa sonra yukarıdan aşağıya).

nrows = 17
ncols = 5
fig, ax = plt.subplots(nrows, ncols, figsize=(18, 21), sharey=True, sharex=True)
with warnings.catch_warnings():
  warnings.simplefilter('ignore')
  ii = -1
  for r in range(nrows):
    for c in range(ncols):
      ii += 1
      idx = county_freq[ii, 0]
      sns.kdeplot(
          posterior_random_weights_final_[:, idx] * log_county_uranium_ppm[idx],
          color='blue',
          alpha=.3,
          shade=True,
          label='TFP',
          ax=ax[r][c])
      sns.kdeplot(
          posterior_random_weights_final_stan[:, idx] *
          log_county_uranium_ppm[idx],
          color='red',
          alpha=.3,
          shade=True,
          label='Stan/rstanarm',
          ax=ax[r][c])
      sns.kdeplot(
          posterior_random_weights_lme4_final_[:, idx] *
          log_county_uranium_ppm[idx],
          color='#F4B400',
          alpha=.7,
          shade=False,
          label='R/lme4',
          ax=ax[r][c])
      ax[r][c].vlines(
          posterior_random_weights_lme4[idx] * log_county_uranium_ppm[idx],
          0,
          5,
          color='#F4B400',
          linestyle='--')
      ax[r][c].set_title(county_name[idx] + ' ({})'.format(idx), y=.7)
      ax[r][c].set_ylim(0, 5)
      ax[r][c].set_xlim(-1., 1.)
      ax[r][c].get_yaxis().set_visible(False)
      if ii == 2:
        ax[r][c].legend(bbox_to_anchor=(1.4, 1.7), fontsize=20, ncol=3)
      else:
        ax[r][c].legend_.remove()
  fig.subplots_adjust(wspace=0.03, hspace=0.1)

8 Sonuç

Bu ortak çalışmada, radon veri kümesine doğrusal bir karma etkili regresyon modeli uyduruyoruz. Üç farklı yazılım paketi denedik: R, Stan ve TensorFlow Probability. Üç farklı yazılım paketi tarafından hesaplanan 85 ardıl dağılımı çizerek sonuçlandırdık.

Ek A: Alternatif Radon HLM (Random Intercept Ekle)

Bu bölümde, her ilçeyle ilişkili rastgele bir kesişimi de olan alternatif bir HLM'yi tanımlıyoruz.

\[\begin{align*} \text{for } & c=1\ldots \text{NumCounties}:\\ & \beta_c \sim \text{MultivariateNormal}\left(\text{loc}=\left[ \begin{array}{c} 0 \\ 0 \end{array}\right] , \text{scale}=\left[\begin{array}{cc} \sigma_{11} & 0 \\ \sigma_{12} & \sigma_{22} \end{array}\right] \right) \\ \text{for } & i=1\ldots \text{NumSamples}:\\ & c_i := \text{County}_i \\ &\eta_i = \underbrace{\omega_0 + \omega_1\text{Floor}_i \vphantom{\log( \text{CountyUraniumPPM}_{c_i}))} }_{\text{fixed effects} } + \underbrace{\beta_{c_i,0} + \beta_{c_i,1}\log( \text{CountyUraniumPPM}_{c_i}))}_{\text{random effects} } \\ &\log(\text{Radon}_i) \sim \text{Normal}(\text{loc}=\eta_i , \text{scale}=\sigma) \end{align*}\]

R'ın içinde lme4 "gösterimde tilde", bu model eşdeğerdir:

log_radon ~ 1 + floor + (1 + log_county_uranium_ppm | county)

Ek B: Genelleştirilmiş Doğrusal Karma Etkili Modeller

Bu bölümde, Hiyerarşik Doğrusal Modellerin ana gövdede kullanılandan daha genel bir karakterizasyonunu veriyoruz. Bu, daha fazla genel model olarak bilinen bir genelleştirilmiş doğrusal karma etki modeline (glmM).

GLMMs genellemeler vardır Jeneralize Lineer Modeller (GLMs). GLMM'ler, numuneye özgü rastgele gürültüyü tahmin edilen doğrusal yanıta dahil ederek GLM'leri genişletir. Bu, kısmen, nadiren görülen özelliklerin daha sık görülen özelliklerle bilgi paylaşmasına izin verdiği için yararlıdır.

Üretken bir süreç olarak, Genelleştirilmiş Doğrusal Karışık Etkiler Modeli (GLMM) şu şekilde karakterize edilir:

\begin{align} \text{için } & r = 1\ldots R: \hspace{2,45cm}\text metin \ & \ \ eta ı \ underbrace {\ vphantom {\ toplamı {r = 1} ^ R} = {hizalanmış} başlar x i '^ \ En \ omega} \ metni {sabit etkiler} + \ underbrace {\ toplamı {r = 1} ^ RZ {r ı} ^ \ En \ beta_ {r, Cı-r, (i)}} \ metni {rastgele etki} \ ve Y_I | x i \ omega {z {r ı}, \ p r} {r = 1} ^ R \ sim \ metni {Dağıtım} (\ metni {ortalama} = g ^ {1 -} (\ eta_i )) \end{hizalanmış} \end{hiza}

nerede:

\begin{align} R &= \text{rastgele efekt gruplarının sayısı}\ |C_r| & = \ Metni {grubu için kategori sayısı \(r\)\ N = \ metni {eğitim numune sayısı} \ x_i, \ omega \ in \ mathbb {R} ^ {D_0} \ D_0 & = \ metni {} sabit etkiler sayısı} (grup altında \ Cı-r (i) = \ metni {kategori \(r\)arasında) \(i\)inci örnek} \ z {r i} \ in \ mathbb {R} ^ { D_r} \ Ar-Ge = \ metni {grup ile ilişkili rastgele etki sayısı \(r\) ^ {D_r \ kez D_r} {S \ \ mathbb {R} \ \ Sigma {r} \}: S \ succ 0 }\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{ters bağlantı işlevi}\ \text{Dağıtım} &=\text{yalnızca ortalaması ile parametrelendirilebilen bazı dağılım} \ bitiş{hiza}

Yani bu, her grubun her kategori bir iid MVN, ilişkili olduğunu söyler \(\beta_{rc}\). Her ne kadar \(\beta_{rc}\) çizer onlar sadece indentically bir grup için dağıtılır, her zaman bağımsız \(r\); ihbar tam bir tane \(\Sigma_r\) her \(r\in\{1,\ldots,R\}\).

Affinely bir, örneğin, grubun özellikleri ile birleştirildiğinde, \(z_{r,i}\), sonuç ile numuneye özgü gürültü \(i\)(aksi takdirde doğrusal bir tepki tahmin inci \(x_i^\top\omega\)).

Biz tahmin zaman \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) Esasen aksi takdirde sinyal mevcut boğmak rastgele etki grubu taşıyan gürültü miktarını tahmin etmeye \(x_i^\top\omega\).

İçin çeşitli seçenekler vardır \(\text{Distribution}\) ve ters bağlantı fonksiyonu , \(g^{-1}\). Ortak seçenekler şunlardır:

• \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
• \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), ve
• \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).

Daha fazla olasılık için bkz tfp.glm modülü.