 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
1। পরিচিতি
এই কোল্যাবে আমরা একটি জনপ্রিয়, খেলনা ডেটাসেটে একটি লিনিয়ার মিক্সড-ইফেক্ট রিগ্রেশন মডেল ফিট করব। আমরা এই হইয়া তিনবার করতে, আর এর ব্যবহার হবে lme4 , স্ট্যান এর মিশ্র-প্রতিক্রিয়া প্যাকেজ, এবং TensorFlow সম্ভাব্যতা (TFP) প্রিমিটিভের। আমরা তিনটিই মোটামুটি একই লাগানো পরামিতি এবং পশ্চাদবর্তী বন্টনগুলি দেখিয়ে উপসংহারে পৌঁছেছি।
আমাদের প্রধান উপসংহার TFP মাপসই মডেলের HLM মত এবং এটি ফলাফল যা অন্যান্য সফটওয়্যার প্যাকেজ সঙ্গে সামঞ্জস্যপূর্ণ হয়, অর্থাত।, উত্পাদন করে প্রয়োজনীয় সাধারণ টুকরা আছে lme4 , rstanarm । এই কোল্যাব তুলনামূলক প্যাকেজগুলির যেকোন কম্পিউটেশনাল দক্ষতার সঠিক প্রতিফলন নয়।
%matplotlib inline
import os
from six.moves import urllib
import numpy as np
import pandas as pd
import warnings
from matplotlib import pyplot as plt
import seaborn as sns
from IPython.core.pylabtools import figsize
figsize(11, 9)
import tensorflow.compat.v1 as tf
import tensorflow_datasets as tfds
import tensorflow_probability as tfp
2 হায়ারার্কিক্যাল লিনিয়ার মডেল
আর, স্ট্যান এবং TFP মধ্যে আমাদের তুলনা, আমরা একটি মাপসই করা হবে স্তরীয় রৈখিক মডেল করার জন্য (HLM) রাডন ডেটা সেটটি জনপ্রিয় প্রণীত Gelman, এট দ্বারা Bayesian ডেটা বিশ্লেষণ। আল (পৃষ্ঠা 559, দ্বিতীয় সংস্করণ; পৃষ্ঠা 250, তৃতীয় সংস্করণ)।
আমরা নিম্নলিখিত উত্পাদনশীল মডেল অনুমান:
\[\begin{align*} \text{for } & c=1\ldots \text{NumCounties}:\\ & \beta_c \sim \text{Normal}\left(\text{loc}=0, \text{scale}=\sigma_C \right) \\ \text{for } & i=1\ldots \text{NumSamples}:\\ &\eta_i = \underbrace{\omega_0 + \omega_1 \text{Floor}_i}_\text{fixed effects} + \underbrace{\beta_{ \text{County}_i} \log( \text{UraniumPPM}_{\text{County}_i}))}_\text{random effects} \\ &\log(\text{Radon}_i) \sim \text{Normal}(\text{loc}=\eta_i , \text{scale}=\sigma_N) \end{align*}\]
আর এর দশকে lme4 "স্বরলিপি টিল্ড", এই মডেল সমতূল্য:
log_radon ~ 1 + floor + (0 + log_uranium_ppm | county)
আমরা MLE পাবেন \(\omega, \sigma_C, \sigma_N\) এর অবর বন্টন (প্রমাণের ওপর নিয়ন্ত্রিত) ব্যবহার \(\{\beta_c\}_{c=1}^\text{NumCounties}\)।
মূলত একই মডেল কিন্তু একটি র্যান্ডম পথিমধ্যে সঙ্গে, দেখতে পরিশিষ্ট ।
HLMs একটি সাধারণ স্পেসিফিকেশন জন্য, দেখুন পরিশিষ্ট B ।
3 ডাটা মুঙ্গিং
এই বিভাগে আমরা প্রাপ্ত radon ডেটা সেটটি এবং এটা আমাদের অধিকৃত মডেল মেনে চলতে করতে কিছু ন্যূনতম প্রাক-প্রক্রিয়াকরণ না।
def load_and_preprocess_radon_dataset(state='MN'):
"""Preprocess Radon dataset as done in "Bayesian Data Analysis" book.
We filter to Minnesota data (919 examples) and preprocess to obtain the
following features:
- `log_uranium_ppm`: Log of soil uranium measurements.
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
# For any missing or invalid activity readings, we'll use a value of `0.1`.
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
county_name = sorted(df.county.unique())
df['county'] = df.county.astype(
pd.api.types.CategoricalDtype(categories=county_name)).cat.codes
county_name = list(map(str.strip, county_name))
df['log_radon'] = df['radon'].apply(np.log)
df['log_uranium_ppm'] = df['Uppm'].apply(np.log)
df = df[['idnum', 'log_radon', 'floor', 'county', 'log_uranium_ppm']]
return df, county_name
radon, county_name = load_and_preprocess_radon_dataset()
# We'll use the following directory to store our preprocessed dataset.
CACHE_DIR = os.path.join(os.sep, 'tmp', 'radon')
# Save processed data. (So we can later read it in R.)
if not tf.gfile.Exists(CACHE_DIR):
tf.gfile.MakeDirs(CACHE_DIR)
with tf.gfile.Open(os.path.join(CACHE_DIR, 'radon.csv'), 'w') as f:
radon.to_csv(f, index=False)
3.1 আপনার ডেটা জানুন
এই বিভাগে আমরা অন্বেষণ radon কেন প্রস্তাবিত মডেল যুক্তিসংগত হতে পারে একটি ভাল ধারনা পেতে ডেটা সেটটি।
radon.head()
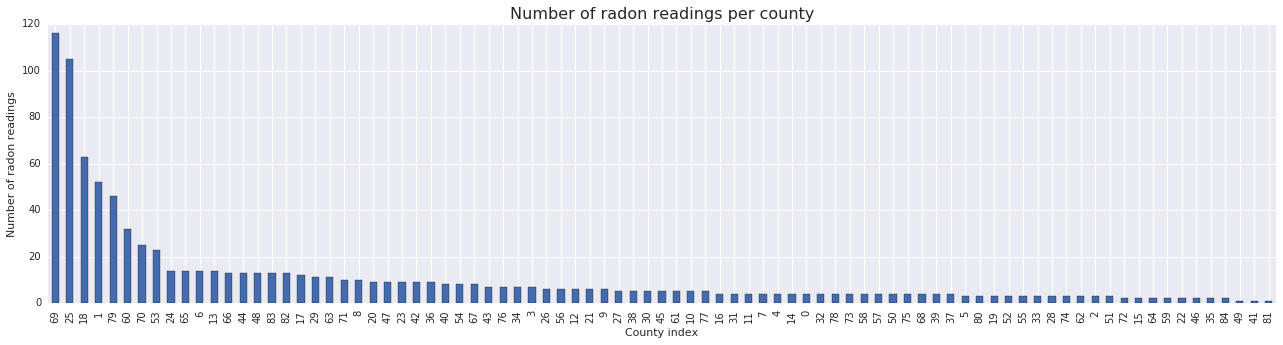
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = radon['county'].value_counts()
county_freq.plot(kind='bar', color='#436bad');
plt.xlabel('County index')
plt.ylabel('Number of radon readings')
plt.title('Number of radon readings per county', fontsize=16)
county_freq = np.array(zip(county_freq.index, county_freq.values)) # We'll use this later.
fig, ax = plt.subplots(ncols=2, figsize=[10, 4]);
radon['log_radon'].plot(kind='density', ax=ax[0]);
ax[0].set_xlabel('log(radon)')
radon['floor'].value_counts().plot(kind='bar', ax=ax[1]);
ax[1].set_xlabel('Floor');
ax[1].set_ylabel('Count');
fig.subplots_adjust(wspace=0.25)
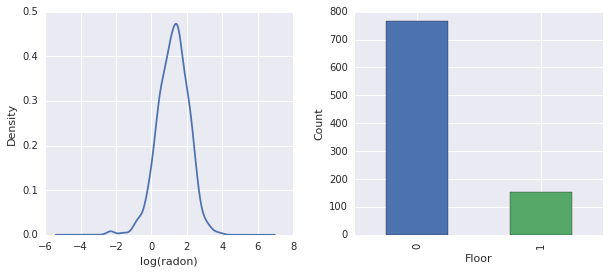
উপসংহার:
- ৮৫টি কাউন্টির লম্বা লেজ আছে। (GLMMs-এ একটি সাধারণ ঘটনা।)
- প্রকৃতপক্ষে \(\log(\text{Radon})\) সংকোচহীন হয়। (সুতরাং লিনিয়ার রিগ্রেশনের অর্থ হতে পারে।)
- রিডিং বেশিরভাগ তৈরি করা হয় \(0\)-th মেঝে; কোন পড়া মেঝে উপরে তৈরি করা হয়েছিল \(1\)। (সুতরাং আমাদের স্থির প্রভাবের শুধুমাত্র দুটি ওজন থাকবে।)
4 এইচএলএম ইন আর
এই বিভাগে আমরা আর এর ব্যবহার lme4 প্যাকেজ সম্ভাব্য মডেলটি উপরে বর্ণিত মাপসই।
suppressMessages({
library('bayesplot')
library('data.table')
library('dplyr')
library('gfile')
library('ggplot2')
library('lattice')
library('lme4')
library('plyr')
library('rstanarm')
library('tidyverse')
RequireInitGoogle()
})
data = read_csv(gfile::GFile('/tmp/radon/radon.csv'))
Parsed with column specification: cols( log_radon = col_double(), floor = col_integer(), county = col_integer(), log_uranium_ppm = col_double() )
head(data)
# A tibble: 6 x 4
log_radon floor county log_uranium_ppm
<dbl> <int> <int> <dbl>
1 0.788 1 0 -0.689
2 0.788 0 0 -0.689
3 1.06 0 0 -0.689
4 0 0 0 -0.689
5 1.13 0 1 -0.847
6 0.916 0 1 -0.847
# https://github.com/stan-dev/example-models/wiki/ARM-Models-Sorted-by-Chapter
radon.model <- lmer(log_radon ~ 1 + floor + (0 + log_uranium_ppm | county), data = data)
summary(radon.model)
Linear mixed model fit by REML ['lmerMod']
Formula: log_radon ~ 1 + floor + (0 + log_uranium_ppm | county)
Data: data
REML criterion at convergence: 2166.3
Scaled residuals:
Min 1Q Median 3Q Max
-4.5202 -0.6064 0.0107 0.6334 3.4111
Random effects:
Groups Name Variance Std.Dev.
county log_uranium_ppm 0.7545 0.8686
Residual 0.5776 0.7600
Number of obs: 919, groups: county, 85
Fixed effects:
Estimate Std. Error t value
(Intercept) 1.47585 0.03899 37.85
floor -0.67974 0.06963 -9.76
Correlation of Fixed Effects:
(Intr)
floor -0.330
qqmath(ranef(radon.model, condVar=TRUE))
$county
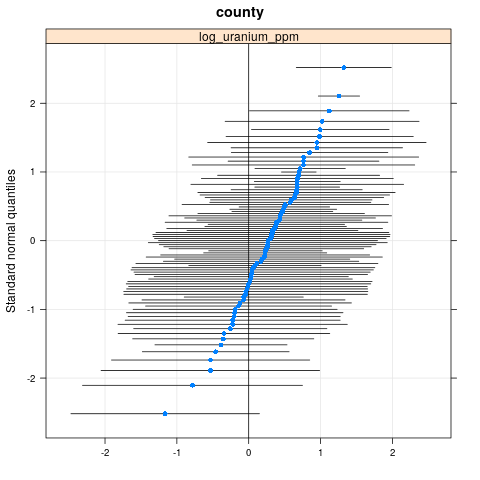
write.csv(as.data.frame(ranef(radon.model, condVar = TRUE)), '/tmp/radon/lme4_fit.csv')
স্ট্যান ইন 5 HLM
এই বিভাগে আমরা ব্যবহার rstanarm হিসাবে একই সূত্র / সিনট্যাক্স ব্যবহার করে একটি স্ট্যান মডেল মাপসই lme4 উপরে মডেল।
ভিন্ন lme4 এবং নীচের মেমরি মডেল, rstanarm একটি সম্পূর্ণরূপে Bayesian মডেল, নিজেদের মধ্যে একটি ডিস্ট্রিবিউশন থেকে টানা পরামিতি সঙ্গে একটি সাধারণ বিন্যাসের থেকে টানা অর্থাত, সকল প্যারামিটার সম্ভাব্য হয়।
fit <- stan_lmer(log_radon ~ 1 + floor + (0 + log_uranium_ppm | county), data = data)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1, Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1, Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1, Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1, Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1, Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1, Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1, Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1, Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1, Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1, Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1, Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1, Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 7.73495 seconds (Warm-up)
2.98852 seconds (Sampling)
10.7235 seconds (Total)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2, Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2, Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2, Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2, Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2, Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2, Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2, Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2, Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2, Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2, Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2, Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2, Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 7.51252 seconds (Warm-up)
3.08653 seconds (Sampling)
10.5991 seconds (Total)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3, Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3, Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3, Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3, Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3, Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3, Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3, Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3, Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3, Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3, Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3, Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3, Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 8.14628 seconds (Warm-up)
3.01001 seconds (Sampling)
11.1563 seconds (Total)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4, Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4, Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4, Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4, Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4, Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4, Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4, Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4, Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4, Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4, Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4, Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4, Iteration: 2000 / 2000 [100%] (Sampling)
Elapsed Time: 7.6801 seconds (Warm-up)
3.23663 seconds (Sampling)
10.9167 seconds (Total)
fit
stan_lmer(formula = log_radon ~ 1 + floor + (0 + log_uranium_ppm |
county), data = data)
Estimates:
Median MAD_SD
(Intercept) 1.5 0.0
floor -0.7 0.1
sigma 0.8 0.0
Error terms:
Groups Name Std.Dev.
county log_uranium_ppm 0.87
Residual 0.76
Num. levels: county 85
Sample avg. posterior predictive
distribution of y (X = xbar):
Median MAD_SD
mean_PPD 1.2 0.0
Observations: 919 Number of unconstrained parameters: 90
color_scheme_set("red")
ppc_dens_overlay(y = fit$y,
yrep = posterior_predict(fit, draws = 50))
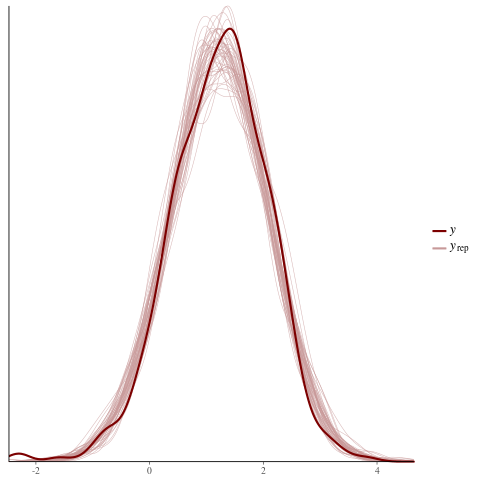
color_scheme_set("brightblue")
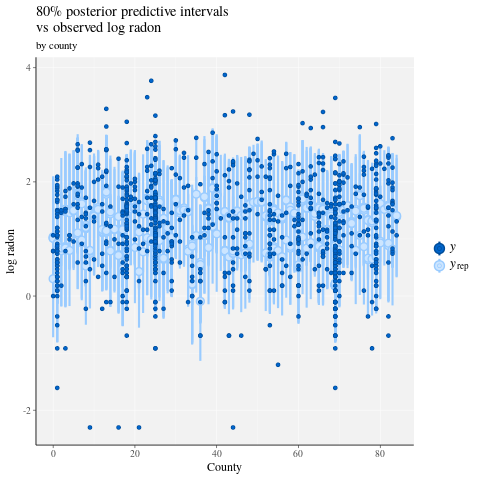
ppc_intervals(
y = data$log_radon,
yrep = posterior_predict(fit),
x = data$county,
prob = 0.8
) +
labs(
x = "County",
y = "log radon",
title = "80% posterior predictive intervals \nvs observed log radon",
subtitle = "by county"
) +
panel_bg(fill = "gray95", color = NA) +
grid_lines(color = "white")
# Write the posterior samples (4000 for each variable) to a CSV.
write.csv(tidy(as.matrix(fit)), "/tmp/radon/stan_fit.csv")
with tf.gfile.Open('/tmp/radon/lme4_fit.csv', 'r') as f:
lme4_fit = pd.read_csv(f, index_col=0)
lme4_fit.head()
পরে ভিজ্যুয়ালাইজেশনের জন্য lme4 থেকে গ্রুপ এলোমেলো প্রভাবগুলির জন্য বিন্দু অনুমান এবং শর্তাধীন মান বিচ্যুতি পুনরুদ্ধার করুন।
posterior_random_weights_lme4 = np.array(lme4_fit.condval, dtype=np.float32)
lme4_prior_scale = np.array(lme4_fit.condsd, dtype=np.float32)
print(posterior_random_weights_lme4.shape, lme4_prior_scale.shape)
(85,) (85,)
lme4 আনুমানিক উপায় এবং মানক বিচ্যুতি ব্যবহার করে কাউন্টি ওজনের জন্য নমুনা আঁকুন।
with tf.Session() as sess:
lme4_dist = tfp.distributions.Independent(
tfp.distributions.Normal(
loc=posterior_random_weights_lme4,
scale=lme4_prior_scale),
reinterpreted_batch_ndims=1)
posterior_random_weights_lme4_final_ = sess.run(lme4_dist.sample(4000))
posterior_random_weights_lme4_final_.shape
(4000, 85)
আমরা স্ট্যান ফিট থেকে কাউন্টি ওজনের পিছনের নমুনাগুলিও পুনরুদ্ধার করি।
with tf.gfile.Open('/tmp/radon/stan_fit.csv', 'r') as f:
samples = pd.read_csv(f, index_col=0)
samples.head()
posterior_random_weights_cols = [
col for col in samples.columns if 'b.log_uranium_ppm.county' in col
]
posterior_random_weights_final_stan = samples[
posterior_random_weights_cols].values
print(posterior_random_weights_final_stan.shape)
(4000, 85)
এই স্ট্যান উদাহরণ দেখায় কিভাবে এক TFP, অর্থাত্, কাছাকাছি সরাসরি সম্ভাব্য মডেল নির্দিষ্ট করে একটি শৈলী মধ্যে LMER বাস্তবায়ন করবে।
6 HLM ইন TF সম্ভাবনা
এই বিভাগে আমরা নিম্নস্তরের TensorFlow সম্ভাব্যতা প্রিমিটিভের (ব্যবহার করবে Distributions আমাদের স্তরীয় রৈখিক মডেল নির্দিষ্ট করার) পাশাপাশি অজানা পরামিতি মাপসই করা হবে।
# Handy snippet to reset the global graph and global session.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
tf.reset_default_graph()
try:
sess.close()
except:
pass
sess = tf.InteractiveSession()
6.1 মডেল নির্দিষ্ট করুন
এই বিভাগে আমরা উল্লেখ মিশ্র প্রতিক্রিয়া মডেল রৈখিক রাডন TFP প্রিমিটিভের ব্যবহার করে। এটি করার জন্য, আমরা দুটি ফাংশন নির্দিষ্ট করি যা দুটি TFP বিতরণ উত্পাদন করে:
-
make_weights_prior: র্যান্ডম ওজন (যা দ্বারা গুন জন্য একটি বহুচলকীয় সাধারন পূর্বে \(\log(\text{UraniumPPM}_{c_i})\) রৈখিক predictor compue করার জন্য)। -
make_log_radon_likelihood: একটি ব্যাচNormalপ্রতিটি পর্যবেক্ষিত উপর ডিস্ট্রিবিউশন \(\log(\text{Radon}_i)\) নির্ভরশীল পরিবর্তনশীল।
আমরা এই ডিস্ট্রিবিউশন আমরা মেমরি ভেরিয়েবল (অর্থাত, ব্যবহার করা আবশ্যক প্রতিটি পরামিতি ঝুলানো হবে যেহেতু tf.get_variable )। যাইহোক, যেহেতু আমরা অনিয়ন্ত্রিত অপ্টিমাইজেশন ব্যবহার করতে চাই, আমাদের অবশ্যই প্রয়োজনীয় শব্দার্থবিদ্যা অর্জনের জন্য বাস্তব-মানগুলিকে সীমাবদ্ধ করার একটি উপায় খুঁজে বের করতে হবে, যেমন, আদর্শ বিচ্যুতির প্রতিনিধিত্ব করে।
inv_scale_transform = lambda y: np.log(y) # Not using TF here.
fwd_scale_transform = tf.exp
নিম্নলিখিত ফাংশন আমাদের পূর্বে, নির্মান \(p(\beta|\sigma_C)\) যেখানে \(\beta\) র্যান্ডম প্রতিক্রিয়া ওজন ও উল্লেখ করে \(\sigma_C\) স্ট্যান্ডার্ড ডেভিয়েশন।
আমরা ব্যবহার tf.make_template তা নিশ্চিত করার জন্য এই ক্রিয়াকলাপের প্রথম কল মেমরি ভেরিয়েবল এটি ব্যবহার করে এবং পরিবর্তনশীল এর বর্তমান মূল্য পুনঃব্যবহারের সব পরবর্তী কল instantiates।
def _make_weights_prior(num_counties, dtype):
"""Returns a `len(log_uranium_ppm)` batch of univariate Normal."""
raw_prior_scale = tf.get_variable(
name='raw_prior_scale',
initializer=np.array(inv_scale_transform(1.), dtype=dtype))
return tfp.distributions.Independent(
tfp.distributions.Normal(
loc=tf.zeros(num_counties, dtype=dtype),
scale=fwd_scale_transform(raw_prior_scale)),
reinterpreted_batch_ndims=1)
make_weights_prior = tf.make_template(
name_='make_weights_prior', func_=_make_weights_prior)
নিম্নলিখিত ফাংশন আমাদের সম্ভাবনা, নির্মান \(p(y|x,\omega,\beta,\sigma_N)\) যেখানে \(y,x\) বোঝাতে প্রতিক্রিয়া এবং প্রমাণ, \(\omega,\beta\) বোঝাতে fixed- এবং র্যান্ডম প্রতিক্রিয়া ওজন, এবং \(\sigma_N\) স্ট্যান্ডার্ড ডেভিয়েশন।
এখানে পুনরায় আমরা ব্যবহার tf.make_template নিশ্চিত করার মেমরি ভেরিয়েবল কল জুড়ে পুনঃব্যবহৃত করা হয়।
def _make_log_radon_likelihood(random_effect_weights, floor, county,
log_county_uranium_ppm, init_log_radon_stddev):
raw_likelihood_scale = tf.get_variable(
name='raw_likelihood_scale',
initializer=np.array(
inv_scale_transform(init_log_radon_stddev), dtype=dtype))
fixed_effect_weights = tf.get_variable(
name='fixed_effect_weights', initializer=np.array([0., 1.], dtype=dtype))
fixed_effects = fixed_effect_weights[0] + fixed_effect_weights[1] * floor
random_effects = tf.gather(
random_effect_weights * log_county_uranium_ppm,
indices=tf.to_int32(county),
axis=-1)
linear_predictor = fixed_effects + random_effects
return tfp.distributions.Normal(
loc=linear_predictor, scale=fwd_scale_transform(raw_likelihood_scale))
make_log_radon_likelihood = tf.make_template(
name_='make_log_radon_likelihood', func_=_make_log_radon_likelihood)
অবশেষে আমরা যৌথ লগ-ঘনত্ব নির্মাণের জন্য পূর্বের এবং সম্ভাব্য জেনারেটর ব্যবহার করি।
def joint_log_prob(random_effect_weights, log_radon, floor, county,
log_county_uranium_ppm, dtype):
num_counties = len(log_county_uranium_ppm)
rv_weights = make_weights_prior(num_counties, dtype)
rv_radon = make_log_radon_likelihood(
random_effect_weights,
floor,
county,
log_county_uranium_ppm,
init_log_radon_stddev=radon.log_radon.values.std())
return (rv_weights.log_prob(random_effect_weights)
+ tf.reduce_sum(rv_radon.log_prob(log_radon), axis=-1))
6.2 প্রশিক্ষণ (প্রত্যাশা সর্বাধিকীকরণের স্টোকাস্টিক আনুমানিক)
আমাদের লিনিয়ার মিক্সড-ইফেক্ট রিগ্রেশন মডেল ফিট করার জন্য, আমরা এক্সপেক্টেশন ম্যাক্সিমাইজেশন অ্যালগরিদম (SAEM) এর একটি স্টোকাস্টিক আনুমানিক সংস্করণ ব্যবহার করব। মূল ধারণাটি হল প্রত্যাশিত যৌথ লগ-ঘনত্ব (ই-পদক্ষেপ) আনুমানিক করতে পশ্চাৎভাগ থেকে নমুনাগুলি ব্যবহার করা। তারপরে আমরা প্যারামিটারগুলি খুঁজে পাই যা এই গণনাকে সর্বাধিক করে তোলে (এম-পদক্ষেপ)। কিছুটা আরও সুনির্দিষ্টভাবে, স্থির-বিন্দু পুনরাবৃত্তি দ্বারা দেওয়া হয়:
\[\begin{align*} \text{E}[ \log p(x, Z | \theta) | \theta_0] &\approx \frac{1}{M} \sum_{m=1}^M \log p(x, z_m | \theta), \quad Z_m\sim p(Z | x, \theta_0) && \text{E-step}\\ &=: Q_M(\theta, \theta_0) \\ \theta_0 &= \theta_0 - \eta \left.\nabla_\theta Q_M(\theta, \theta_0)\right|_{\theta=\theta_0} && \text{M-step} \end{align*}\]
যেখানে \(x\) প্রমাণ, উল্লেখ করে \(Z\) কিছু সুপ্ত পরিবর্তনশীল যা আউট প্রান্তিক করা প্রয়োজন, এবং \(\theta,\theta_0\) সম্ভব parameterizations।
আরো পুঙ্খানুপুঙ্খ ব্যাখ্যার জন্য দেখুন, বার্নার্ড Delyon, আঙুরের ছিবড়ে Lavielle, এরিক, Moulines (অ্যান। পরিসংখ্যানবিৎ।, 1999) দ্বারা ই.এম. আলগোরিদিম একটি সম্ভাব্যতার সূত্রাবলি পড়তা সংস্করণের কনভার্জেন্স ।
ই-পদক্ষেপ গণনা করতে, আমাদের পশ্চাৎভাগ থেকে নমুনা নিতে হবে। যেহেতু আমাদের পশ্চাৎভাগ থেকে নমুনা নেওয়া সহজ নয়, তাই আমরা হ্যামিলটোনিয়ান মন্টে কার্লো (HMC) ব্যবহার করি। HMC হল একটি মন্টে কার্লো মার্কভ চেইন পদ্ধতি যা নতুন নমুনা প্রস্তাব করার জন্য অস্বাভাবিক পোস্টেরিয়র লগ-ঘনত্বের গ্রেডিয়েন্ট (wrt স্টেট, প্যারামিটার নয়) ব্যবহার করে।
অস্বাভাবিক পোস্টেরিয়র লগ-ঘনত্ব নির্দিষ্ট করা সহজ--এটি শুধুমাত্র জয়েন্ট লগ-ঘনত্ব "পিন করা" যা আমরা শর্ত দিতে চাই।
# Specify unnormalized posterior.
dtype = np.float32
log_county_uranium_ppm = radon[
['county', 'log_uranium_ppm']].drop_duplicates().values[:, 1]
log_county_uranium_ppm = log_county_uranium_ppm.astype(dtype)
def unnormalized_posterior_log_prob(random_effect_weights):
return joint_log_prob(
random_effect_weights=random_effect_weights,
log_radon=dtype(radon.log_radon.values),
floor=dtype(radon.floor.values),
county=np.int32(radon.county.values),
log_county_uranium_ppm=log_county_uranium_ppm,
dtype=dtype)
আমরা এখন একটি HMC ট্রানজিশন কার্নেল তৈরি করে ই-স্টেপ সেটআপ সম্পূর্ণ করি।
মন্তব্য:
আমরা ব্যবহার
state_stop_gradient=Trueমাধ্যমে backpropping থেকে M-পদক্ষেপ এমসিএমসি থেকে স্বপক্ষে প্রতিরোধ। (রিকল, আমরা মাধ্যমে backprop করার প্রয়োজন নেই কারণ আমাদের ই-পদক্ষেপ ইচ্ছাকৃতভাবে পূর্ববর্তী সব থেকে বহুল পরিচিত estimators এ স্থিতিমাপ হয়।)আমরা ব্যবহার
tf.placeholderযাতে যখন আমরা অবশেষে আমাদের মেমরি গ্রাফ চালানো, আমরা পরবর্তী পুনরাবৃত্তিতে এর চেইন এর মান হিসাবে পূর্ববর্তী পুনরাবৃত্তির এর র্যান্ডম এমসিএমসি নমুনা খাওয়ানোর পারবেন না।আমরা TFP এর অভিযোজিত ব্যবহার
step_sizeঅনুসন্ধানমূলক,tfp.mcmc.hmc_step_size_update_fn।
# Set-up E-step.
step_size = tf.get_variable(
'step_size',
initializer=np.array(0.2, dtype=dtype),
trainable=False)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
num_leapfrog_steps=2,
step_size=step_size,
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(
num_adaptation_steps=None),
state_gradients_are_stopped=True)
init_random_weights = tf.placeholder(dtype, shape=[len(log_county_uranium_ppm)])
posterior_random_weights, kernel_results = tfp.mcmc.sample_chain(
num_results=3,
num_burnin_steps=0,
num_steps_between_results=0,
current_state=init_random_weights,
kernel=hmc)
আমরা এখন এম-স্টেপ সেট আপ করি। এটি মূলত টিএফ-এ করা একটি অপ্টিমাইজেশনের মতোই।
# Set-up M-step.
loss = -tf.reduce_mean(kernel_results.accepted_results.target_log_prob)
global_step = tf.train.get_or_create_global_step()
learning_rate = tf.train.exponential_decay(
learning_rate=0.1,
global_step=global_step,
decay_steps=2,
decay_rate=0.99)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss, global_step=global_step)
আমরা কিছু হাউসকিপিং কাজ দিয়ে শেষ করি। আমাদের অবশ্যই TF কে বলতে হবে যে সমস্ত ভেরিয়েবল শুরু করা হয়েছে। আমরা আমাদের মেমরি ভেরিয়েবল হ্যান্ডলগুলি তৈরি তাই আমরা করতে পারেন print পদ্ধতি প্রতিটি পুনরাবৃত্তির তাদের মান।
# Initialize all variables.
init_op = tf.initialize_all_variables()
# Grab variable handles for diagnostic purposes.
with tf.variable_scope('make_weights_prior', reuse=True):
prior_scale = fwd_scale_transform(tf.get_variable(
name='raw_prior_scale', dtype=dtype))
with tf.variable_scope('make_log_radon_likelihood', reuse=True):
likelihood_scale = fwd_scale_transform(tf.get_variable(
name='raw_likelihood_scale', dtype=dtype))
fixed_effect_weights = tf.get_variable(
name='fixed_effect_weights', dtype=dtype)
6.3 চালান
এই বিভাগে আমরা আমাদের SAEM TF গ্রাফ চালাই। এখানে প্রধান কৌশল হল এইচএমসি কার্নেল থেকে আমাদের শেষ ড্র পরবর্তী পুনরাবৃত্তিতে খাওয়ানো। এই আমাদের ব্যবহারের মাধ্যমে অর্জিত হয় feed_dict মধ্যে sess.run কল।
init_op.run()
w_ = np.zeros([len(log_county_uranium_ppm)], dtype=dtype)
%%time
maxiter = int(1500)
num_accepted = 0
num_drawn = 0
for i in range(maxiter):
[
_,
global_step_,
loss_,
posterior_random_weights_,
kernel_results_,
step_size_,
prior_scale_,
likelihood_scale_,
fixed_effect_weights_,
] = sess.run([
train_op,
global_step,
loss,
posterior_random_weights,
kernel_results,
step_size,
prior_scale,
likelihood_scale,
fixed_effect_weights,
], feed_dict={init_random_weights: w_})
w_ = posterior_random_weights_[-1, :]
num_accepted += kernel_results_.is_accepted.sum()
num_drawn += kernel_results_.is_accepted.size
acceptance_rate = num_accepted / num_drawn
if i % 100 == 0 or i == maxiter - 1:
print('global_step:{:>4} loss:{: 9.3f} acceptance:{:.4f} '
'step_size:{:.4f} prior_scale:{:.4f} likelihood_scale:{:.4f} '
'fixed_effect_weights:{}'.format(
global_step_, loss_.mean(), acceptance_rate, step_size_,
prior_scale_, likelihood_scale_, fixed_effect_weights_))
global_step: 0 loss: 1966.948 acceptance:1.0000 step_size:0.2000 prior_scale:1.0000 likelihood_scale:0.8529 fixed_effect_weights:[ 0. 1.] global_step: 100 loss: 1165.385 acceptance:0.6205 step_size:0.2040 prior_scale:0.9568 likelihood_scale:0.7611 fixed_effect_weights:[ 1.47523439 -0.66043079] global_step: 200 loss: 1149.851 acceptance:0.6766 step_size:0.2081 prior_scale:0.7465 likelihood_scale:0.7665 fixed_effect_weights:[ 1.48918796 -0.67058587] global_step: 300 loss: 1163.464 acceptance:0.6811 step_size:0.2040 prior_scale:0.8445 likelihood_scale:0.7594 fixed_effect_weights:[ 1.46291411 -0.67586178] global_step: 400 loss: 1158.846 acceptance:0.6808 step_size:0.2081 prior_scale:0.8377 likelihood_scale:0.7574 fixed_effect_weights:[ 1.47349834 -0.68823022] global_step: 500 loss: 1154.193 acceptance:0.6766 step_size:0.1961 prior_scale:0.8546 likelihood_scale:0.7564 fixed_effect_weights:[ 1.47703862 -0.67521363] global_step: 600 loss: 1163.903 acceptance:0.6783 step_size:0.2040 prior_scale:0.9491 likelihood_scale:0.7587 fixed_effect_weights:[ 1.48268366 -0.69667786] global_step: 700 loss: 1163.894 acceptance:0.6767 step_size:0.1961 prior_scale:0.8644 likelihood_scale:0.7617 fixed_effect_weights:[ 1.4719094 -0.66897118] global_step: 800 loss: 1153.689 acceptance:0.6742 step_size:0.2123 prior_scale:0.8366 likelihood_scale:0.7609 fixed_effect_weights:[ 1.47345769 -0.68343043] global_step: 900 loss: 1155.312 acceptance:0.6718 step_size:0.2040 prior_scale:0.8633 likelihood_scale:0.7581 fixed_effect_weights:[ 1.47426116 -0.6748783 ] global_step:1000 loss: 1151.278 acceptance:0.6690 step_size:0.2081 prior_scale:0.8737 likelihood_scale:0.7581 fixed_effect_weights:[ 1.46990883 -0.68891817] global_step:1100 loss: 1156.858 acceptance:0.6676 step_size:0.2040 prior_scale:0.8716 likelihood_scale:0.7584 fixed_effect_weights:[ 1.47386014 -0.6796245 ] global_step:1200 loss: 1166.247 acceptance:0.6653 step_size:0.2000 prior_scale:0.8748 likelihood_scale:0.7588 fixed_effect_weights:[ 1.47389269 -0.67626756] global_step:1300 loss: 1165.263 acceptance:0.6636 step_size:0.2040 prior_scale:0.8771 likelihood_scale:0.7581 fixed_effect_weights:[ 1.47612262 -0.67752427] global_step:1400 loss: 1158.108 acceptance:0.6640 step_size:0.2040 prior_scale:0.8748 likelihood_scale:0.7587 fixed_effect_weights:[ 1.47534692 -0.6789524 ] global_step:1499 loss: 1161.030 acceptance:0.6638 step_size:0.1941 prior_scale:0.8738 likelihood_scale:0.7589 fixed_effect_weights:[ 1.47624075 -0.67875224] CPU times: user 1min 16s, sys: 17.6 s, total: 1min 33s Wall time: 27.9 s
দেখে মনে হচ্ছে ~1500 ধাপের পরে, আমাদের প্যারামিটারের অনুমান স্থির হয়ে গেছে।
6.4 ফলাফল
এখন যেহেতু আমরা পরামিতিগুলি ফিট করেছি, আসুন একটি বড় সংখ্যক পশ্চাৎপদ নমুনা তৈরি করি এবং ফলাফলগুলি অধ্যয়ন করি।
%%time
posterior_random_weights_final, kernel_results_final = tfp.mcmc.sample_chain(
num_results=int(15e3),
num_burnin_steps=int(1e3),
current_state=init_random_weights,
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
num_leapfrog_steps=2,
step_size=step_size))
[
posterior_random_weights_final_,
kernel_results_final_,
] = sess.run([
posterior_random_weights_final,
kernel_results_final,
], feed_dict={init_random_weights: w_})
CPU times: user 1min 42s, sys: 26.6 s, total: 2min 8s Wall time: 35.1 s
print('prior_scale: ', prior_scale_)
print('likelihood_scale: ', likelihood_scale_)
print('fixed_effect_weights: ', fixed_effect_weights_)
print('acceptance rate final: ', kernel_results_final_.is_accepted.mean())
prior_scale: 0.873799 likelihood_scale: 0.758913 fixed_effect_weights: [ 1.47624075 -0.67875224] acceptance rate final: 0.7448
এখন আমরা একটি বক্স এবং জুলপি এর ডায়াগ্রাম গঠন করা \(\beta_c \log(\text{UraniumPPM}_c)\) র্যান্ডম-প্রভাব। আমরা কাউন্টি ফ্রিকোয়েন্সি হ্রাস করে এলোমেলো প্রভাবগুলি অর্ডার করব৷
x = posterior_random_weights_final_ * log_county_uranium_ppm
I = county_freq[:, 0]
x = x[:, I]
cols = np.array(county_name)[I]
pw = pd.DataFrame(x)
pw.columns = cols
fig, ax = plt.subplots(figsize=(25, 4))
ax = pw.boxplot(rot=80, vert=True);
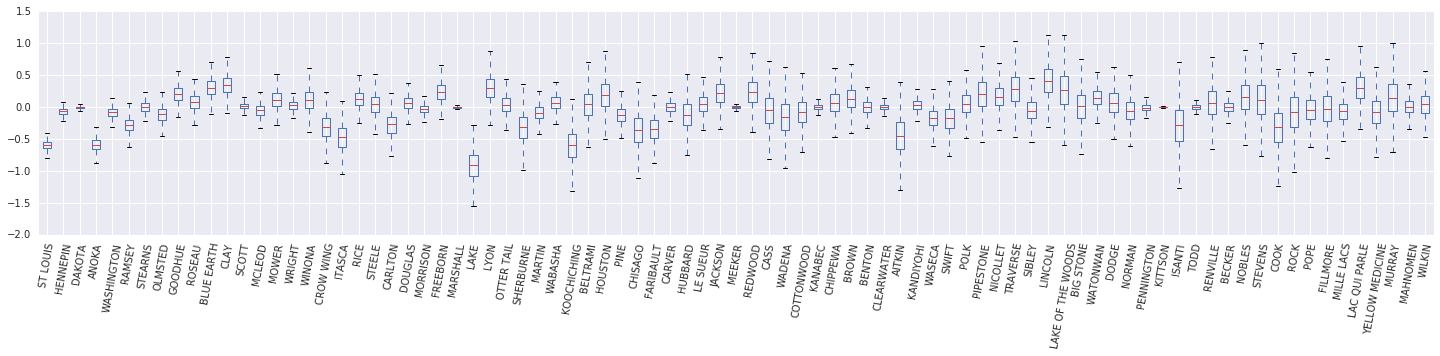
এই বক্স এবং জুলপি ডায়াগ্রাম থেকে আমরা যে কাউন্টি পর্যায়ের ভ্যারিয়েন্স পালন \(\log(\text{UraniumPPM})\) কাউন্টি হিসাবে র্যান্ডম প্রতিক্রিয়া বৃদ্ধি কম ডেটাসেটে প্রতিনিধিত্ব করা হয়। স্বজ্ঞাতভাবে এটি বোধগম্য হয়-- যদি আমাদের কাছে এর জন্য কম প্রমাণ থাকে তবে একটি নির্দিষ্ট কাউন্টির প্রভাব সম্পর্কে আমাদের কম নিশ্চিত হওয়া উচিত।
7 পাশ-পাশ-পাশ-পাশের তুলনা
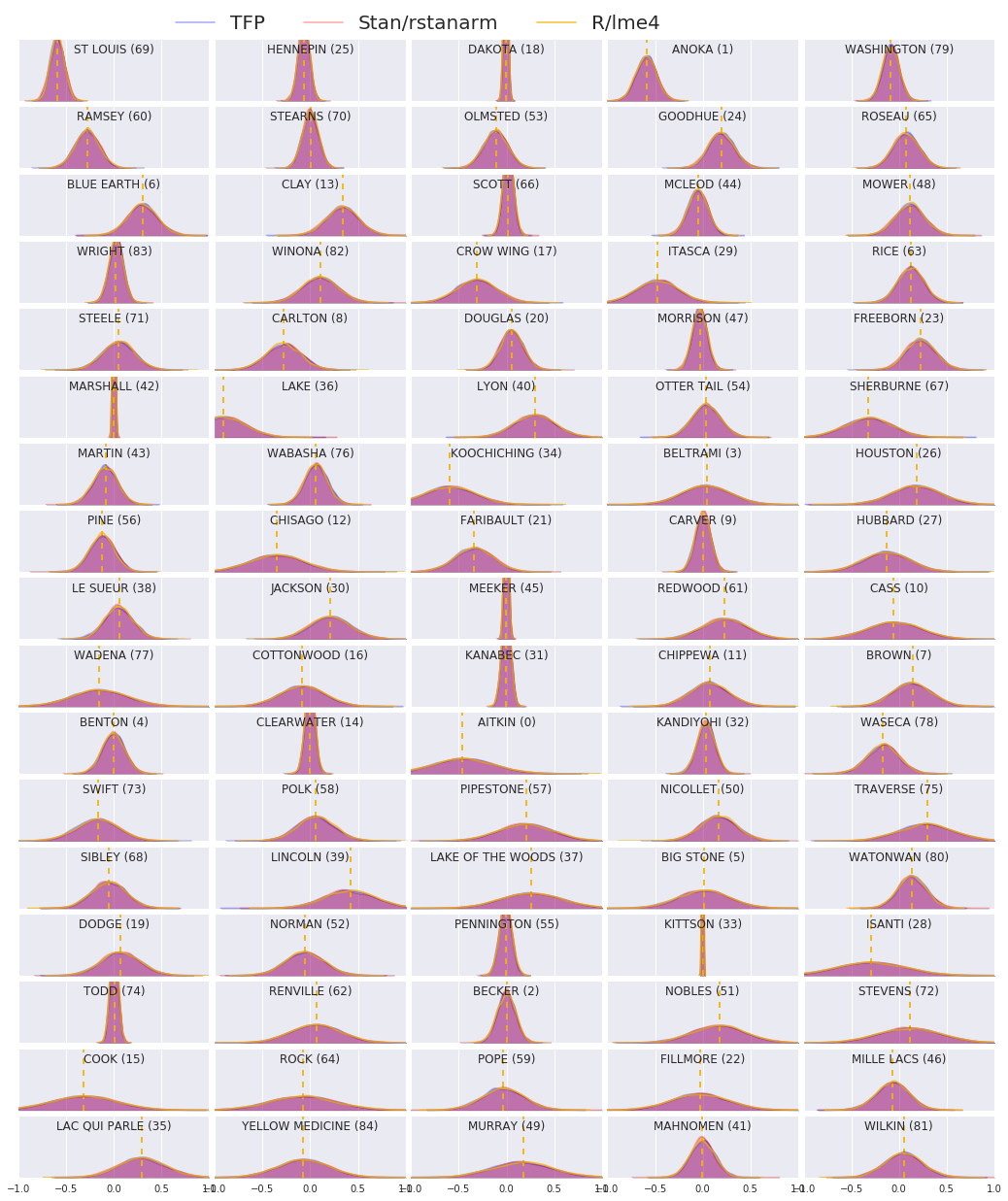
আমরা এখন তিনটি পদ্ধতির ফলাফল তুলনা করি। এটি করার জন্য, আমরা স্ট্যান এবং TFP দ্বারা উত্পন্ন পশ্চাদবর্তী নমুনাগুলির অ-প্যারামিটারিক অনুমানগুলি গণনা করব৷ আমরা parameteric (প্রায়) আর এর দ্বারা উত্পাদিত অনুমান বিরুদ্ধে তুলনা করবে lme4 প্যাকেজ।
নিম্নলিখিত প্লটটি মিনেসোটার প্রতিটি কাউন্টির জন্য প্রতিটি ওজনের পশ্চাৎভাগ বন্টন চিত্রিত করে। আমরা স্ট্যান (লাল), TFP (নীল), এবং আর এর জন্য ফলাফল দেখান lme4 (কমলা)। আমরা স্ট্যান এবং TFP-এর ফলাফলগুলিকে ছায়া দিই, এইভাবে দুইজন সম্মত হলে বেগুনি দেখতে আশা করি। সরলতার জন্য আমরা R থেকে ফলাফলগুলিকে ছায়া দিই না। প্রতিটি সাবপ্লট একটি একক কাউন্টির প্রতিনিধিত্ব করে এবং রাস্টার স্ক্যানের ক্রমানুসারে ডিসেন্ডিং ফ্রিকোয়েন্সিতে অর্ডার দেওয়া হয় (অর্থাৎ, বাম থেকে ডান তারপর উপরে-থেকে-নিচে)।
nrows = 17
ncols = 5
fig, ax = plt.subplots(nrows, ncols, figsize=(18, 21), sharey=True, sharex=True)
with warnings.catch_warnings():
warnings.simplefilter('ignore')
ii = -1
for r in range(nrows):
for c in range(ncols):
ii += 1
idx = county_freq[ii, 0]
sns.kdeplot(
posterior_random_weights_final_[:, idx] * log_county_uranium_ppm[idx],
color='blue',
alpha=.3,
shade=True,
label='TFP',
ax=ax[r][c])
sns.kdeplot(
posterior_random_weights_final_stan[:, idx] *
log_county_uranium_ppm[idx],
color='red',
alpha=.3,
shade=True,
label='Stan/rstanarm',
ax=ax[r][c])
sns.kdeplot(
posterior_random_weights_lme4_final_[:, idx] *
log_county_uranium_ppm[idx],
color='#F4B400',
alpha=.7,
shade=False,
label='R/lme4',
ax=ax[r][c])
ax[r][c].vlines(
posterior_random_weights_lme4[idx] * log_county_uranium_ppm[idx],
0,
5,
color='#F4B400',
linestyle='--')
ax[r][c].set_title(county_name[idx] + ' ({})'.format(idx), y=.7)
ax[r][c].set_ylim(0, 5)
ax[r][c].set_xlim(-1., 1.)
ax[r][c].get_yaxis().set_visible(False)
if ii == 2:
ax[r][c].legend(bbox_to_anchor=(1.4, 1.7), fontsize=20, ncol=3)
else:
ax[r][c].legend_.remove()
fig.subplots_adjust(wspace=0.03, hspace=0.1)
8 উপসংহার
এই কোলাবে আমরা রেডন ডেটাসেটের সাথে একটি লিনিয়ার মিক্সড-ইফেক্ট রিগ্রেশন মডেল ফিট করি। আমরা তিনটি ভিন্ন সফ্টওয়্যার প্যাকেজ চেষ্টা করেছি: R, Stan, এবং TensorFlow সম্ভাব্যতা। আমরা তিনটি ভিন্ন সফ্টওয়্যার প্যাকেজ দ্বারা গণনা করা 85টি পোস্টেরিয়র ডিস্ট্রিবিউশন প্লট করে শেষ করেছি।
পরিশিষ্ট A: বিকল্প রেডন এইচএলএম (এড র্যান্ডম ইন্টারসেপ্ট)
এই বিভাগে আমরা একটি বিকল্প HLM বর্ণনা করি যার প্রতিটি কাউন্টির সাথে যুক্ত একটি এলোমেলো বাধা রয়েছে।
\[\begin{align*} \text{for } & c=1\ldots \text{NumCounties}:\\ & \beta_c \sim \text{MultivariateNormal}\left(\text{loc}=\left[ \begin{array}{c} 0 \\ 0 \end{array}\right] , \text{scale}=\left[\begin{array}{cc} \sigma_{11} & 0 \\ \sigma_{12} & \sigma_{22} \end{array}\right] \right) \\ \text{for } & i=1\ldots \text{NumSamples}:\\ & c_i := \text{County}_i \\ &\eta_i = \underbrace{\omega_0 + \omega_1\text{Floor}_i \vphantom{\log( \text{CountyUraniumPPM}_{c_i}))} }_{\text{fixed effects} } + \underbrace{\beta_{c_i,0} + \beta_{c_i,1}\log( \text{CountyUraniumPPM}_{c_i}))}_{\text{random effects} } \\ &\log(\text{Radon}_i) \sim \text{Normal}(\text{loc}=\eta_i , \text{scale}=\sigma) \end{align*}\]
আর এর দশকে lme4 "স্বরলিপি টিল্ড", এই মডেল সমতূল্য:
log_radon ~ 1 + floor + (1 + log_county_uranium_ppm | county)
পরিশিষ্ট বি: সাধারণ রৈখিক মিশ্র-প্রভাব মডেল
এই বিভাগে আমরা প্রধান অংশে যা ব্যবহার করা হয় তার চেয়ে হায়ারার্কিকাল লিনিয়ার মডেলগুলির একটি আরও সাধারণ বৈশিষ্ট্য দিই। এই আরও সাধারণ মডেল একটি হিসাবে পরিচিত হয় সাধারণ রৈখিক মিশ্র প্রতিক্রিয়া মডেল (GLMM)।
GLMMs এর সরলীকরণ হয় সাধারণ রৈখিক মডেল (GLMs)। GLMMগুলি পূর্বাভাসিত রৈখিক প্রতিক্রিয়ার মধ্যে নমুনা নির্দিষ্ট র্যান্ডম শব্দকে অন্তর্ভুক্ত করে GLMগুলিকে প্রসারিত করে। এটি আংশিকভাবে উপযোগী কারণ এটি খুব কমই দেখা বৈশিষ্ট্যগুলিকে আরও সাধারণভাবে দেখা বৈশিষ্ট্যগুলির সাথে তথ্য ভাগ করার অনুমতি দেয়৷
একটি উৎপাদক প্রক্রিয়া হিসাবে, একটি সাধারণ রৈখিক মিশ্র প্রভাব মডেল (GLMM) দ্বারা চিহ্নিত করা হয়:
\begin{align} \text{for } & r = 1\ldots R: \hspace{2.45cm}\text \ & \ শুরু {প্রান্তিককৃত} এবং \ ETA আমি \ underbrace {\ vphantom {\ সমষ্টি {R = 1} ^ আর} = এক্স আমি ^ \ শীর্ষ \ ওমেগা} \ টেক্সট {স্থির প্রভাব} + + \ underbrace {\ সমষ্টি {R = 1} ^ আর z- র {R, আমি} ^ \ শীর্ষ \ beta_ {R, সি দ (ঝ)}} \ টেক্সট {র্যান্ডম প্রভাব} \ & Y_i | এক্স আমি, \ ওমেগা, {z- র {R, আমি}, \ বিটা R} {R = 1} ^ r \ সিম \ টেক্সট {বিতরণ} (\ টেক্সট {গড়} = ছ ^ {- 1} (\ eta_i )) \end{aligned} \end{align}
কোথায়:
শুরু করুন{align} R &= \text{এলোমেলো-প্রভাব গোষ্ঠীর সংখ্যা}\ |C_r| & = \ টেক্সট {দলের জন্য আরও সংখ্যা \(r\)\ n & = \ টেক্সট {প্রশিক্ষণ নমুনার সংখ্যা} \ x_i, \ ওমেগা & \ এ \ mathbb {r} ^ {D_0} \ D_0 & = \ টেক্সট {} নির্দিষ্ট প্রভাব সংখ্যা} \ সি দ (ঝ) & = \ টেক্সট {বিভাগ (গ্রুপ অধীনে \(r\)এর) \(i\)তম নমুনা} \ z- র {R, আমি} এবং \ এ \ mathbb {r} ^ { D_r} \ ডি R & = \ টেক্সট {দলের সঙ্গে যুক্ত র্যান্ডম-প্রতিক্রিয়া সংখ্যা \(r\) ^ {D_r \ বার D_r}} \ সিগমা {R} এবং \ {এস \ এ \ mathbb {আর এ \}: এস \ succ 0 }\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{inverse link function}\ \text{Distribution} &=\text{কিছু ডিস্ট্রিবিউশন প্যারামিটারাইজ করা যায় শুধুমাত্র এর গড় দ্বারা} \ শেষ{সারিবদ্ধ}
অর্থাৎ, এই বলছেন যে প্রতিটি দলের প্রতিটি বিভাগ একটি IID MVN, এর সাথে সংশ্লিষ্ট \(\beta_{rc}\)। যদিও \(\beta_{rc}\) স্বপক্ষে সবসময় তারা শুধুমাত্র indentically একটি দলের জন্য বিতরণ করা হয় স্বাধীন হয়, \(r\); নোটিশ সেখানে ঠিক এক \(\Sigma_r\) প্রত্যেকের জন্য \(r\in\{1,\ldots,R\}\)।
Affinely নমুনা গ্রুপের বৈশিষ্ট্য, সঙ্গে মিলিত যখন \(z_{r,i}\), ফলাফলে নমুনা-নির্দিষ্ট গোলমাল \(i\)-th রৈখিক প্রতিক্রিয়া (যা অন্যথায় হয় পূর্বাভাস \(x_i^\top\omega\))।
আমরা যখন অনুমান \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) আমরা মূলত গোলমাল পরিমাণ একটি র্যান্ডম প্রতিক্রিয়া গ্রুপ বহন করে যা অন্যথায় মধ্যে সংকেত উপস্থিত আউট মজান হবে আনুমানিক হিসাব করছি \(x_i^\top\omega\)।
সেখানে বিকল্প বিভিন্ন হয় \(\text{Distribution}\) এবং বিপরীত লিংক ফাংশন , \(g^{-1}\)। সাধারণ পছন্দ হল:
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), এবং,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\)।
আরো সম্ভাবনার জন্য, দেখুন tfp.glm মডিউল।
