 Ver no TensorFlow.org Ver no TensorFlow.org |  Executar no Google Colab Executar no Google Colab |  Ver fonte no GitHub Ver fonte no GitHub |  Baixar caderno Baixar caderno |
Neste colab, exploramos a regressão do processo Gaussiano usando TensorFlow e Probabilidade do TensorFlow. Geramos algumas observações ruidosas de algumas funções conhecidas e ajustamos modelos GP a esses dados. Em seguida, amostramos a partir do GP posterior e plotamos os valores das funções amostradas nas grades em seus domínios.
Fundo
Deixe- \(\mathcal{X}\) ser qualquer conjunto. Um processo de Gauss (GP) é um conjunto de variáveis aleatórias indexados por \(\mathcal{X}\) tal que se\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) é qualquer subconjunto finito, a densidade marginal\(p(X_1 = x_1, \ldots, X_n = x_n)\) é multivariada Gaussiana. Qualquer distribuição gaussiana é completamente especificada por seu primeiro e segundo momentos centrais (média e covariância), e os GPs não são exceção. Podemos especificar um GP completamente em termos de sua média função \(\mu : \mathcal{X} \to \mathbb{R}\) função e covariância\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). A maior parte do poder expressivo dos GPs está encapsulado na escolha da função de covariância. Por várias razões, a função de covariância também é referido como uma função kernel. Ela é necessária apenas para ser simétrica e definida positiva (ver Cap. 4 de Rasmussen & Williams ). Abaixo, fazemos uso do kernel de covariância ExponenciadaQuadrática. Sua forma é
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
onde \(\sigma^2\) é chamado de 'amplitude' e \(\lambda\) a escala de comprimento. Os parâmetros do kernel podem ser selecionados por meio de um procedimento de otimização de máxima verossimilhança.
Uma amostra completa de um GP compreende uma função real ao longo de todo o espaço\(\mathcal{X}\) e é, na prática impraticável para perceber; frequentemente, escolhe-se um conjunto de pontos para observar uma amostra e desenha valores de função nesses pontos. Isso é obtido por amostragem de um gaussiano multivariado apropriado (dimensão finita).
Observe que, de acordo com a definição acima, qualquer distribuição multivariada multivariada de dimensão finita também é um processo gaussiano. Normalmente, quando alguém se refere a um GP, está implícito que o conjunto índice é algum \(\mathbb{R}^n\)e vamos realmente fazer essa suposição aqui.
Uma aplicação comum dos processos gaussianos no aprendizado de máquina é a regressão do processo gaussiano. A ideia é que queremos estimar uma função desconhecida dadas observações ruidosas \(\{y_1, \ldots, y_N\}\) da função em um número finito de pontos \(\{x_1, \ldots x_N\}.\) Imaginamos um processo generativo
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Como observado acima, a função amostrada é impossível de calcular, uma vez que exigiríamos seu valor em um número infinito de pontos. Em vez disso, considera-se uma amostra finita de um Gaussiano multivariado.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Observe o expoente \(\frac{1}{2}\) na matriz de covariância: isso denota uma decomposição Cholesky. O cálculo de Cholesky é necessário porque o MVN é uma distribuição familiar em escala local. Infelizmente a decomposição Cholesky é computacionalmente caro, tendo \(O(N^3)\) tempo e \(O(N^2)\) espaço. Grande parte da literatura GP concentra-se em lidar com esse pequeno expoente aparentemente inócuo.
É comum considerar a função média anterior constante, geralmente zero. Além disso, algumas convenções notacionais são convenientes. Um escreve frequentemente \(\mathbf{f}\) para o vetor finito de valores da função amostrados. Um número de notações interessantes são utilizados para a matriz de covariâncias, resultante da aplicação de \(k\) para pares de entradas. Seguinte (Quiñonero-Candela, 2005) , podemos constatar que os componentes da matriz são covariâncias de valores da função em determinados pontos de entrada. Assim, podemos designar a matriz de covariância como \(K_{AB}\)onde \(A\) e \(B\) são alguns indicadores de recolha de valores da função ao longo das dadas dimensões da matriz.
Por exemplo, dado dados observados \((\mathbf{x}, \mathbf{y})\) com os valores da função latente implícitas \(\mathbf{f}\), podemos escrever
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
Da mesma forma, podemos misturar conjuntos de entradas, como em
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
onde supomos há \(N\) entradas de treinamento e \(T\) entradas de teste. O processo gerador acima pode então ser escrito de forma compacta como
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
A operação de amostragem na primeira linha produz um conjunto finito de \(N\) valores da função de uma Gaussiana multivariada - não uma função inteira como na notação acima GP desenhar. A segunda linha descreve um conjunto de \(N\) chama de Gaussianas univariadas centrado nos vários valores de função, com ruído observação fixo \(\sigma^2\).
Com o modelo gerador acima em vigor, podemos prosseguir para considerar o problema de inferência posterior. Isso produz uma distribuição posterior sobre os valores da função em um novo conjunto de pontos de teste, condicionado nos dados ruidosos observados do processo acima.
Com a notação acima no lugar, podemos compacta escrever a distribuição preditiva posterior sobre o futuro (ruidosos) observações condicional nas entradas e dados de treinamento correspondente da seguinte forma (para mais detalhes, consulte §2.2 de Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
Onde
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
e
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
Importações
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Exemplo: Regressão exata de GP em dados sinusoidais ruidosos
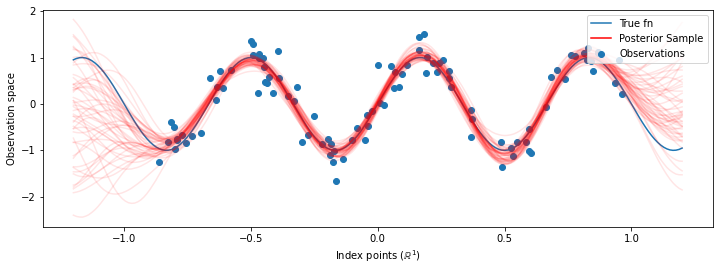
Aqui, geramos dados de treinamento a partir de uma sinusóide ruidosa e, a seguir, amostramos um monte de curvas da parte posterior do modelo de regressão GP. Usamos Adam para optimizar os hiperparâmetros do kernel (que minimizar a probabilidade de log negativo dos dados sob o anterior). Plotamos a curva de treinamento, seguida pela função verdadeira e as amostras posteriores.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Vamos colocar priores sobre os hiperparâmetros do kernel, e escrever a distribuição conjunta dos hiperparâmetros e dados observados usando tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Podemos verificar a sanidade de nossa implementação verificando se podemos amostrar do anterior e calcular a densidade logarítmica de uma amostra.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Agora vamos otimizar para encontrar os valores dos parâmetros com maior probabilidade posterior. Vamos definir uma variável para cada parâmetro e restringir seus valores para serem positivos.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Para condicionar o modelo em nossos dados observados, vamos definir um target_log_prob função, o que leva os (ainda a ser inferidas) hiperparâmetros do kernel.
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
Marginalizando hiperparâmetros com HMC
Em vez de otimizar os hiperparâmetros, vamos tentar integrá-los com o Hamiltoniano de Monte Carlo. Primeiro definiremos e executaremos um amostrador para desenhar aproximadamente a partir da distribuição posterior sobre os hiperparâmetros do kernel, dadas as observações.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
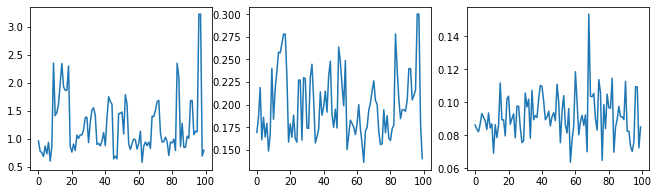
Vamos verificar a sanidade do amostrador examinando os traços do hiperparâmetro.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Agora, em vez da construção de um único GP com os hiperparâmetros optimizadas, que construir a distribuição preditivo posterior como uma mistura de GPs, cada um definido por uma amostra a partir da distribuição posterior ao longo hiperparâmetros. Isso se integra aproximadamente aos parâmetros posteriores por meio da amostragem de Monte Carlo para calcular a distribuição preditiva marginal em locais não observados.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
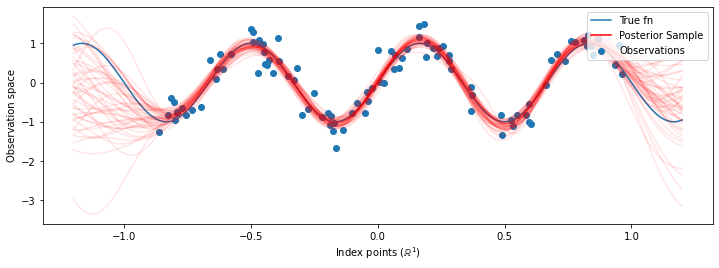
Embora as diferenças sejam sutis nesse caso, em geral, esperaríamos que a distribuição preditiva posterior generalizasse melhor (dê maior probabilidade de dados mantidos) do que apenas usando os parâmetros mais prováveis como fizemos acima.
