 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
W ramach tej współpracy badamy regresję procesu Gaussa za pomocą TensorFlow i TensorFlow Probability. Generujemy zaszumione obserwacje z niektórych znanych funkcji i dopasowujemy modele GP do tych danych. Następnie pobieramy próbki z a posteriori GP i wykreślamy próbkowane wartości funkcji na siatkach w ich domenach.
Tło
Niech \(\mathcal{X}\) być dowolny zestaw. Sposób Gaussa (GP) jest zbiór zmiennych losowych indeksowanych przez \(\mathcal{X}\) taka, że jeśli\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) jest każda podgrupa skończonego krańcowa gęstość\(p(X_1 = x_1, \ldots, X_n = x_n)\) jest wieloczynnikowa Gaussa. Każdy rozkład Gaussa jest całkowicie określony przez jego pierwszy i drugi moment centralny (średnia i kowariancja), a GP nie są wyjątkiem. Możemy określić GP całkowicie pod względem swojej średniej funkcja \(\mu : \mathcal{X} \to \mathbb{R}\) funkcji i kowariancji\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). Większość ekspresyjnej mocy GP jest zawarta w wyborze funkcji kowariancji. Z różnych powodów, funkcja kowariancji jest również określana jako funkcja jądra. Wymagane jest jedynie, aby być symetryczna i dodatnio określona (patrz rozdz. 4 z Rasmussen & Williams ). Poniżej korzystamy z jądra kowariancji ExponentiatedQuadratic. Jego forma to
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
gdzie \(\sigma^2\) nazywa się „Amplituda” i \(\lambda\) skali długości. Parametry jądra można wybrać za pomocą procedury optymalizacji maksymalnej wiarygodności.
Pełną próbki z GP obejmuje funkcję prawdziwego wycenione na całej przestrzeni\(\mathcal{X}\) i jest w praktyce niewykonalne zrealizować; często wybiera się zbiór punktów, w których obserwuje się próbkę i rysuje w tych punktach wartości funkcji. Osiąga się to poprzez próbkowanie z odpowiedniego (skończenie wymiarowego) wielowymiarowego Gaussa.
Należy zauważyć, że zgodnie z powyższą definicją każdy skończenie wymiarowy wielowymiarowy rozkład Gaussa jest również procesem Gaussa. Zazwyczaj, gdy ktoś odnosi się do lekarza, jest niejawna, że zbiór indeks jest jakiś \(\mathbb{R}^n\)i będziemy rzeczywiście uczynić to założenie tutaj.
Powszechnym zastosowaniem procesów gaussowskich w uczeniu maszynowym jest regresja procesów gaussowskich. Chodzi o to, że chcemy oszacować nieznaną funkcję podane hałaśliwe obserwacje \(\{y_1, \ldots, y_N\}\) funkcji w skończonej liczbie punktów \(\{x_1, \ldots x_N\}.\) sobie wyobrazić proces generatywny
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Jak wspomniano powyżej, funkcja próbkowana jest niemożliwa do obliczenia, ponieważ wymagalibyśmy jej wartości w nieskończonej liczbie punktów. Zamiast tego rozważamy skończoną próbkę z wielowymiarowego Gaussa.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Uwaga wykładnik \(\frac{1}{2}\) na macierzy kowariancji: oznacza to rozkład Cholesky'iego. Obliczenie Cholesky jest konieczne, ponieważ MVN jest dystrybucją rodziny w skali lokalizacji. Niestety rozkład choleskiego jest kosztowne obliczeniowo, biorąc \(O(N^3)\) czas i \(O(N^2)\) miejsca. Znaczna część literatury lekarzy rodzinnych koncentruje się na radzeniu sobie z tym pozornie nieszkodliwym małym wykładnikiem.
Powszechnie przyjmuje się, że poprzednia funkcja średniej jest stała, często zero. Wygodne są również niektóre konwencje notacji. Często pisze \(\mathbf{f}\) dla skończonego wektora próbą wartości funkcji. Wiele interesujących zapisów są wykorzystywane do macierzy kowariancji wynikające ze stosowania \(k\) par nakładów. Następujący (Quiñonero-Candela, 2005) , możemy zauważyć, że elementy macierzy kowariancji są wartości funkcji na poszczególnych punktów wejściowych. W ten sposób można oznaczać jako macierz kowariancji \(K_{AB}\)gdzie \(A\) i \(B\) pewne wskaźniki zbiór wartości funkcji wzdłuż zadanych wymiarów macierzy.
Na przykład, biorąc pod uwagę obserwowane dane \((\mathbf{x}, \mathbf{y})\) z domniemanych wartości funkcji utajony \(\mathbf{f}\), możemy napisać
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
Podobnie możemy mieszać zestawy wejść, jak w
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
gdzie założymy istnieją \(N\) wejścia szkoleniowych oraz \(T\) wejścia testowe. Powyższy proces generatywny można następnie zapisać zwięźle jako
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
Operacja pobierania próbek w pierwszej linii daje skończony zestaw \(N\) wartości funkcji z wielowymiarowej Gaussa - nie całą funkcję jak w notacji powyżej GP Draw. Drugi wiersz określa zbiór \(N\) czerpie jednowymiarowe Gaussians skupione w różnych wartości funkcji z szumem stałym obserwacji \(\sigma^2\).
Mając powyższy model generatywny, możemy przystąpić do rozważania problemu wnioskowania a posteriori. Daje to rozkład a posteriori nad wartościami funkcji w nowym zestawie punktów testowych, uwarunkowany obserwowanymi zaszumionymi danymi z powyższego procesu.
Z powyższego zapisu w miejscu, możemy pisać zwięźle tylnej dystrybucję predykcyjną nad przyszłością (głośno) obserwacje uzależnione od odpowiadających wejść i danych treningowych następująco (więcej szczegółów, patrz p.2.2 z Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
gdzie
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
oraz
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
Import
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Przykład: Dokładna regresja GP na zaszumionych danych sinusoidalnych
Tutaj generujemy dane treningowe z hałaśliwej sinusoidy, a następnie próbkujemy kilka krzywych z tyłu modelu regresji GP. Używamy Adama celu optymalizacji hiperparametrów jądra (możemy zminimalizować ujemny logarytm prawdopodobieństwa danych w ramach wcześniej). Wykreślamy krzywą treningową, a następnie prawdziwą funkcję i próbki tylne.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Umieścimy prawdopodobieństwa a priori na hiperparametrów jądra i napisać wspólną dystrybucję hiperparametrów i zaobserwowanych danych z wykorzystaniem tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Możemy sprawdzić poprawność naszej implementacji, weryfikując, czy możemy pobrać próbkę z poprzedniej, i obliczyć gęstość logów próbki.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Teraz zoptymalizujmy, aby znaleźć wartości parametrów z najwyższym prawdopodobieństwem a posteriori. Zdefiniujemy zmienną dla każdego parametru i ograniczymy ich wartości do wartości dodatnich.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Klimatyzowanie model na naszych zaobserwowanych danych, będziemy definiować target_log_prob funkcję, która przyjmuje (wciąż należy wnioskować) hiperparametrów jądra.
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
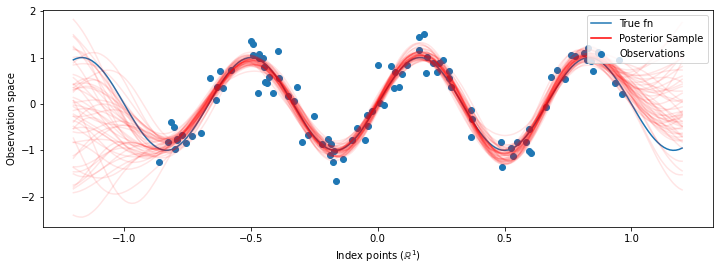
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
Marginalizacja hiperparametrów za pomocą HMC
Zamiast optymalizować hiperparametry, spróbujmy zintegrować je z hamiltonianem Monte Carlo. Najpierw zdefiniujemy i uruchomimy próbnik, aby w przybliżeniu wyciągnąć z rozkładu a posteriori hiperparametrów jądra, biorąc pod uwagę obserwacje.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
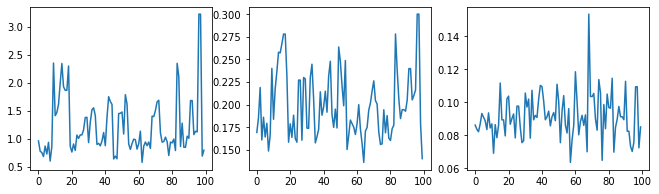
Sprawdźmy rozsądnie próbnik, badając ślady hiperparametrów.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Teraz zamiast konstruowania jednego lekarza ze zoptymalizowanym hiperparametrów, skonstruować tylną rozkład predykcyjną jak mieszanina GPS, takie, jak zdefiniowano dla próbki z tylnej podziału na hiperparametrów. To w przybliżeniu integruje parametry tylne za pomocą próbkowania Monte Carlo, aby obliczyć marginalny rozkład predykcyjny w nieobserwowanych lokalizacjach.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
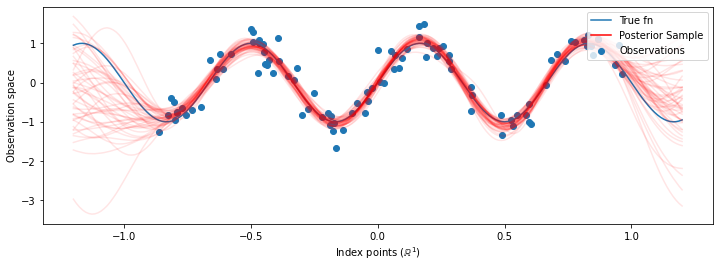
Chociaż w tym przypadku różnice są subtelne, ogólnie rzecz biorąc, spodziewalibyśmy się, że rozkład predykcyjny a posteriori będzie uogólniał lepiej (dał większe prawdopodobieństwo wstrzymanym danym) niż tylko przy użyciu najbardziej prawdopodobnych parametrów, jak to zrobiliśmy powyżej.
