 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
In questa collaborazione, esploriamo la regressione del processo gaussiano utilizzando TensorFlow e TensorFlow Probability. Generiamo alcune osservazioni rumorose da alcune funzioni note e adattiamo i modelli GP a quei dati. Quindi campioniamo dal GP posteriore e tracciamo i valori della funzione campionata su griglie nei loro domini.
Sfondo
Lasciate \(\mathcal{X}\) essere qualsiasi insieme. Un processo gaussiano (GP) è un insieme di variabili casuali indicizzati da \(\mathcal{X}\) tale che se\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) è un qualsiasi sottoinsieme finito, la densità marginale\(p(X_1 = x_1, \ldots, X_n = x_n)\) è multivariata gaussiana. Qualsiasi distribuzione gaussiana è completamente specificata dal suo primo e secondo momento centrale (media e covarianza) e i GP non fanno eccezione. Siamo in grado di specificare un GP completamente in termini di media funzione di \(\mu : \mathcal{X} \to \mathbb{R}\) funzione e la covarianza\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). La maggior parte del potere espressivo dei GP è incapsulato nella scelta della funzione di covarianza. Per varie ragioni, la funzione di covarianza è indicato anche come una funzione del kernel. E 'necessario solo per essere simmetrica e definita positiva (vedi cap. 4 di Rasmussen & Williams ). Di seguito utilizziamo il kernel di covarianza ExponentiatedQuadratic. La sua forma è
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
dove \(\sigma^2\) è chiamato 'ampiezza' e \(\lambda\) la scala di lunghezza. I parametri del kernel possono essere selezionati tramite una procedura di ottimizzazione della massima verosimiglianza.
Un campione completo da un medico di famiglia comprende una funzione a valori reali sopra l'intero spazio\(\mathcal{X}\) ed è in pratica poco pratico da realizzare; spesso si sceglie un insieme di punti in cui osservare un campione e si disegnano valori di funzione in questi punti. Ciò si ottiene campionando da una gaussiana multivariata appropriata (di dimensione finita).
Si noti che, secondo la definizione di cui sopra, qualsiasi distribuzione gaussiana multivariata a dimensione finita è anche un processo gaussiano. Di solito, quando si parla di un GP, è implicito che l'insieme degli indici è una certa \(\mathbb{R}^n\)e ci sarà davvero rendere questa ipotesi qui.
Un'applicazione comune dei processi gaussiani nell'apprendimento automatico è la regressione dei processi gaussiani. L'idea è che vogliamo stimare una funzione sconosciuta formulate Osservazioni rumorosi \(\{y_1, \ldots, y_N\}\) della funzione in un numero finito di punti \(\{x_1, \ldots x_N\}.\) Immaginiamo un processo generativo
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Come notato sopra, la funzione campionata è impossibile da calcolare, poiché si richiederebbe il suo valore in un numero infinito di punti. Invece, si considera un campione finito da una gaussiana multivariata.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Nota l'esponente \(\frac{1}{2}\) sulla matrice di covarianza: ciò denota una decomposizione di Cholesky. Il calcolo di Cholesky è necessario perché MVN è una distribuzione familiare su scala di posizione. Purtroppo la decomposizione di Cholesky è computazionalmente costoso, prendendo \(O(N^3)\) tempo e \(O(N^2)\) spazio. Gran parte della letteratura GP si concentra sulla gestione di questo piccolo esponente apparentemente innocuo.
È comune assumere la funzione media precedente come costante, spesso zero. Inoltre, alcune convenzioni di notazione sono convenienti. Spesso si scrive \(\mathbf{f}\) per il finito vettore di valori di funzione campionati. Un certo numero di notazioni interessanti sono utilizzate per la matrice di covarianza risultante dall'applicazione del \(k\) a coppie di ingressi. Seguendo (Quiñonero-Candela, 2005) , si nota che i componenti della matrice sono covarianza di valori della funzione in particolari punti di ingresso. Così possiamo denotare la matrice di covarianza come \(K_{AB}\)dove \(A\) e \(B\) sono alcuni indicatori della raccolta di valori della funzione lungo le date dimensioni della matrice.
Ad esempio, in dati osservati \((\mathbf{x}, \mathbf{y})\) con valori della funzione latente implicite \(\mathbf{f}\), possiamo scrivere
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
Allo stesso modo, possiamo mescolare insiemi di input, come in
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
dove si suppone ci sono \(N\) ingressi di formazione, e \(T\) ingressi di prova. Il processo generativo di cui sopra può quindi essere scritto in modo compatto come
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
L'operazione di campionamento nella prima riga produce un insieme finito di \(N\) valori di funzione da una gaussiana multivariata - non un intero funzione come nella notazione sopra GP disegnare. La seconda riga descrive un insieme di \(N\) attinge univariate gaussiane centrate ai vari valori di funzione, con il rumore di osservazione fisso \(\sigma^2\).
Con il suddetto modello generativo in atto, possiamo procedere a considerare il problema dell'inferenza a posteriori. Ciò produce una distribuzione a posteriori sui valori della funzione in una nuova serie di punti di prova, condizionata dai dati rumorosi osservati dal processo di cui sopra.
Con la notazione di cui sopra a posto, siamo in grado di scrivere in modo compatto la distribuzione predittiva posteriori sul futuro (rumoroso) osservazioni subordinata corrispondenti ingressi e dati di allenamento nel modo seguente (per maggiori dettagli, vedi §2.2 di Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
dove
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
e
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
Importazioni
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Esempio: regressione GP esatta su dati sinusoidali rumorosi
Qui generiamo dati di addestramento da una sinusoide rumorosa, quindi campioniamo un gruppo di curve dalla parte posteriore del modello di regressione GP. Usiamo Adam per ottimizzare le iperparametri kernel (minimizziamo il registro di probabilità negativo dei dati ai sensi della precedente). Tracciamo la curva di addestramento, seguita dalla funzione vera e dai campioni posteriori.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Metteremo priori sulle iperparametri del kernel, e scriviamo la distribuzione congiunta dei iperparametri ei dati osservati utilizzando tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Possiamo controllare l'integrità della nostra implementazione verificando che possiamo campionare dal precedente e calcolare la densità di log di un campione.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Ora ottimizziamo per trovare i valori dei parametri con la più alta probabilità a posteriori. Definiremo una variabile per ogni parametro e limiteremo i loro valori a essere positivi.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Per condizionare il modello dei nostri dati osservati, definiremo un target_log_prob funzione, che prende le (ancora da dedurre) iperparametri kernel.
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
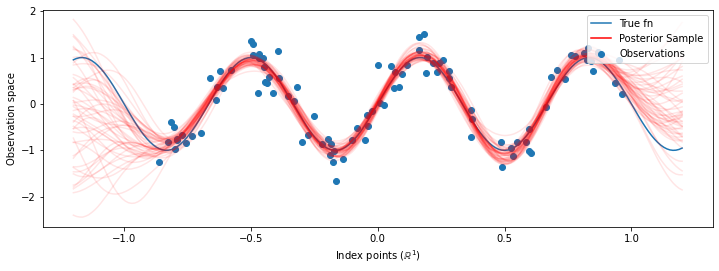
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
Emarginazione degli iperparametri con HMC
Invece di ottimizzare gli iperparametri, proviamo a integrarli con il Monte Carlo hamiltoniano. Per prima cosa definiremo ed eseguiremo un campionatore per attingere approssimativamente dalla distribuzione a posteriori sugli iperparametri del kernel, date le osservazioni.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
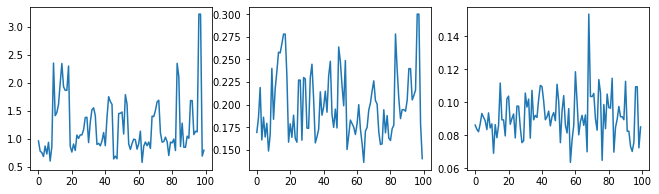
Controlliamo l'integrità del campionatore esaminando le tracce degli iperparametri.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Ora invece di costruire un singolo GP con le iperparametri ottimizzate, si costruisce la distribuzione predittiva posteriori come una miscela di GP, ciascuno definito da un campione dalla distribuzione a posteriori su iperparametri. Questo si integra approssimativamente sui parametri posteriori tramite il campionamento Monte Carlo per calcolare la distribuzione predittiva marginale in posizioni non osservate.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
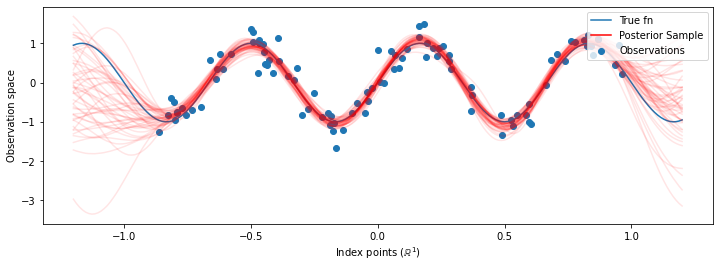
Sebbene le differenze in questo caso siano sottili, in generale, ci aspetteremmo che la distribuzione predittiva a posteriori si generalizzi meglio (dando una maggiore probabilità ai dati trattenuti) rispetto all'utilizzo dei parametri più probabili come abbiamo fatto sopra.
