 Voir sur TensorFlow.org Voir sur TensorFlow.org |  Exécuter dans Google Colab Exécuter dans Google Colab |  Voir la source sur GitHub Voir la source sur GitHub |  Télécharger le cahier Télécharger le cahier |
Dans cette collaboration, nous explorons la régression de processus gaussien à l'aide de TensorFlow et TensorFlow Probability. Nous générons des observations bruitées à partir de certaines fonctions connues et adaptons des modèles GP à ces données. Nous échantillonnons ensuite à partir du modèle a posteriori GP et traçons les valeurs de fonction échantillonnées sur des grilles dans leurs domaines.
Fond
Que \(\mathcal{X}\) un ensemble quelconque. Un processus gaussien (GP) est un ensemble de variables aléatoires indexées par \(\mathcal{X}\) de telle sorte que si\(\{X_1, \ldots, X_n\} \subset \mathcal{X}\) toute partie finie, la densité marginale\(p(X_1 = x_1, \ldots, X_n = x_n)\) est gaussienne multivariée. Toute distribution gaussienne est complètement spécifiée par ses premier et deuxième moments centraux (moyenne et covariance), et les GP ne font pas exception. Nous pouvons spécifier un GP complètement en termes de sa fonction moyenne \(\mu : \mathcal{X} \to \mathbb{R}\) et la fonction covariance\(k : \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). La plupart du pouvoir expressif des GP est encapsulé dans le choix de la fonction de covariance. Pour diverses raisons, la fonction de covariance est également appelée en fonction du noyau. Il est nécessaire que d'être symétrique et définie positive (voir Ch. 4 Rasmussen & Williams ). Ci-dessous, nous utilisons le noyau de covariance ExponentiatedQuadratic. Sa forme est
\[ k(x, x') := \sigma^2 \exp \left( \frac{\|x - x'\|^2}{\lambda^2} \right) \]
où \(\sigma^2\) est appelée la « amplitude » et \(\lambda\) l'échelle de longueur. Les paramètres du noyau peuvent être sélectionnés via une procédure d'optimisation par maximum de vraisemblance.
Un échantillon complet d'un médecin généraliste comprend une fonction à valeur réelle sur l'ensemble de l' espace\(\mathcal{X}\) et est en pratique impossible de réaliser; souvent, on choisit un ensemble de points auxquels observer un échantillon et dessine des valeurs de fonction à ces points. Ceci est réalisé par échantillonnage à partir d'une gaussienne multivariée appropriée (de dimension finie).
Notez que, selon la définition ci-dessus, toute distribution gaussienne multivariée de dimension finie est également un processus gaussien. En général, quand on se réfère à un médecin généraliste, il est implicite que l'ensemble d'indices est une \(\mathbb{R}^n\)et nous allons en effet faire cette hypothèse ici.
Une application courante des processus gaussiens en apprentissage automatique est la régression des processus gaussiens. L'idée est que nous voulons estimer une fonction inconnue donné des observations bruitées \(\{y_1, \ldots, y_N\}\) de la fonction à un nombre fini de points \(\{x_1, \ldots x_N\}.\) Nous imaginons un processus génératif
\[ \begin{align} f \sim \: & \textsf{GaussianProcess}\left( \text{mean_fn}=\mu(x), \text{covariance_fn}=k(x, x')\right) \\ y_i \sim \: & \textsf{Normal}\left( \text{loc}=f(x_i), \text{scale}=\sigma\right), i = 1, \ldots, N \end{align} \]
Comme indiqué ci-dessus, la fonction échantillonnée est impossible à calculer, car nous aurions besoin de sa valeur en un nombre infini de points. Au lieu de cela, on considère un échantillon fini d'une gaussienne multivariée.
\[ \begin{gather} \begin{bmatrix} f(x_1) \\ \vdots \\ f(x_N) \end{bmatrix} \sim \textsf{MultivariateNormal} \left( \: \text{loc}= \begin{bmatrix} \mu(x_1) \\ \vdots \\ \mu(x_N) \end{bmatrix} \:,\: \text{scale}= \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix}^{1/2} \: \right) \end{gather} \\ y_i \sim \textsf{Normal} \left( \text{loc}=f(x_i), \text{scale}=\sigma \right) \]
Notez l'exposant \(\frac{1}{2}\) sur la matrice de covariance: on désigne une décomposition de Cholesky. Le calcul du Cholesky est nécessaire car le MVN est une distribution familiale à l'échelle de l'emplacement. Malheureusement , la décomposition de Cholesky est cher informatiquement, en \(O(N^3)\) temps et \(O(N^2)\) espace. Une grande partie de la littérature GP se concentre sur le traitement de ce petit exposant apparemment inoffensif.
Il est courant de considérer que la fonction moyenne a priori est constante, souvent nulle. De plus, certaines conventions de notation sont pratiques. On écrit souvent \(\mathbf{f}\) pour le vecteur fini de valeurs de fonction échantillonnées. Un certain nombre de notations intéressantes sont utilisés pour la matrice de covariance résultant de l'application de \(k\) à des paires d'entrées. A la suite (Quiñonero-Candela, 2005) , nous notons que les composants de la matrice sont covariances des valeurs de la fonction aux points d'entrée particuliers. Ainsi , nous pouvons noterons la matrice de covariance comme \(K_{AB}\)où \(A\) et \(B\) quelques indicateurs de la collecte des valeurs de fonction le long des dimensions de la matrice donnée.
Par exemple, les données observées étant donné \((\mathbf{x}, \mathbf{y})\) avec des valeurs de la fonction latente implicite \(\mathbf{f}\), nous pouvons écrire
\[ K_{\mathbf{f},\mathbf{f} } = \begin{bmatrix} k(x_1, x_1) & \cdots & k(x_1, x_N) \\ \vdots & \ddots & \vdots \\ k(x_N, x_1) & \cdots & k(x_N, x_N) \\ \end{bmatrix} \]
De même, nous pouvons mélanger des ensembles d'entrées, comme dans
\[ K_{\mathbf{f},*} = \begin{bmatrix} k(x_1, x^*_1) & \cdots & k(x_1, x^*_T) \\ \vdots & \ddots & \vdots \\ k(x_N, x^*_1) & \cdots & k(x_N, x^*_T) \\ \end{bmatrix} \]
où l' on suppose qu'il ya des \(N\) entrées de formation et \(T\) entrées de test. Le processus génératif ci-dessus peut alors être écrit de manière compacte comme
\[ \begin{align} \mathbf{f} \sim \: & \textsf{MultivariateNormal} \left( \text{loc}=\mathbf{0}, \text{scale}=K_{\mathbf{f},\mathbf{f} }^{1/2} \right) \\ y_i \sim \: & \textsf{Normal} \left( \text{loc}=f_i, \text{scale}=\sigma \right), i = 1, \ldots, N \end{align} \]
L'opération d'échantillonnage sur la première ligne fournit un ensemble fini de \(N\) valeurs de fonction à partir d' une gaussienne multivariée - pas une fonction entière comme dans la notation ci - dessus GP dessiner. La deuxième ligne décrit un ensemble de \(N\) tire de gaussiennes unidimensionnelles centré sur les différentes valeurs de la fonction, avec le bruit d'observation fixe \(\sigma^2\).
Avec le modèle génératif ci-dessus en place, nous pouvons procéder à l'examen du problème d'inférence postérieure. Cela donne une distribution postérieure sur les valeurs de fonction à un nouvel ensemble de points de test, conditionnée sur les données bruitées observées du processus ci-dessus.
Avec la notation ci - dessus en place, nous pouvons écrire la distribution compacte prédictive a posteriori sur des observations futures (bruyants) sous condition sur les entrées et les données correspondantes de formation comme suit (pour plus de détails, voir § 2.2 de Rasmussen & Williams ).
\[ \mathbf{y}^* \mid \mathbf{x}^*, \mathbf{x}, \mathbf{y} \sim \textsf{Normal} \left( \text{loc}=\mathbf{\mu}^*, \text{scale}=(\Sigma^*)^{1/2} \right), \]
où
\[ \mathbf{\mu}^* = K_{*,\mathbf{f} }\left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} \mathbf{y} \]
et
\[ \Sigma^* = K_{*,*} - K_{*,\mathbf{f} } \left(K_{\mathbf{f},\mathbf{f} } + \sigma^2 I \right)^{-1} K_{\mathbf{f},*} \]
Importations
import time
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
tfb = tfp.bijectors
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
tf.enable_v2_behavior()
from mpl_toolkits.mplot3d import Axes3D
%pylab inline
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
%config InlineBackend.figure_format = 'png'
Populating the interactive namespace from numpy and matplotlib
Exemple : Régression GP exacte sur des données sinusoïdales bruyantes
Ici, nous générons des données d'entraînement à partir d'une sinusoïde bruyante, puis nous échantillonnons un ensemble de courbes à partir de la partie postérieure du modèle de régression GP. Nous utilisons Adam pour optimiser les hyperparamètres du noyau (nous réduisons la probabilité de log négatif des données sous l'avant). Nous traçons la courbe d'apprentissage, suivie de la vraie fonction et des échantillons postérieurs.
def sinusoid(x):
return np.sin(3 * np.pi * x[..., 0])
def generate_1d_data(num_training_points, observation_noise_variance):
"""Generate noisy sinusoidal observations at a random set of points.
Returns:
observation_index_points, observations
"""
index_points_ = np.random.uniform(-1., 1., (num_training_points, 1))
index_points_ = index_points_.astype(np.float64)
# y = f(x) + noise
observations_ = (sinusoid(index_points_) +
np.random.normal(loc=0,
scale=np.sqrt(observation_noise_variance),
size=(num_training_points)))
return index_points_, observations_
# Generate training data with a known noise level (we'll later try to recover
# this value from the data).
NUM_TRAINING_POINTS = 100
observation_index_points_, observations_ = generate_1d_data(
num_training_points=NUM_TRAINING_POINTS,
observation_noise_variance=.1)
Nous allons mettre prieurs sur les hyperparamètres du noyau et écrire la distribution conjointe des hyperparamètres et les données observées en utilisant tfd.JointDistributionNamed .
def build_gp(amplitude, length_scale, observation_noise_variance):
"""Defines the conditional dist. of GP outputs, given kernel parameters."""
# Create the covariance kernel, which will be shared between the prior (which we
# use for maximum likelihood training) and the posterior (which we use for
# posterior predictive sampling)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
# Create the GP prior distribution, which we will use to train the model
# parameters.
return tfd.GaussianProcess(
kernel=kernel,
index_points=observation_index_points_,
observation_noise_variance=observation_noise_variance)
gp_joint_model = tfd.JointDistributionNamed({
'amplitude': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'length_scale': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observation_noise_variance': tfd.LogNormal(loc=0., scale=np.float64(1.)),
'observations': build_gp,
})
Nous pouvons vérifier l'intégrité de notre implémentation en vérifiant que nous pouvons échantillonner à partir du précédent et calculer la densité logarithmique d'un échantillon.
x = gp_joint_model.sample()
lp = gp_joint_model.log_prob(x)
print("sampled {}".format(x))
print("log_prob of sample: {}".format(lp))
sampled {'observation_noise_variance': <tf.Tensor: shape=(), dtype=float64, numpy=2.067952217184325>, 'length_scale': <tf.Tensor: shape=(), dtype=float64, numpy=1.154435715487831>, 'amplitude': <tf.Tensor: shape=(), dtype=float64, numpy=5.383850737703549>, 'observations': <tf.Tensor: shape=(100,), dtype=float64, numpy=
array([-2.37070577, -2.05363838, -0.95152824, 3.73509388, -0.2912646 ,
0.46112342, -1.98018513, -2.10295857, -1.33589756, -2.23027226,
-2.25081374, -0.89450835, -2.54196452, 1.46621647, 2.32016193,
5.82399989, 2.27241034, -0.67523432, -1.89150197, -1.39834474,
-2.33954116, 0.7785609 , -1.42763627, -0.57389025, -0.18226098,
-3.45098732, 0.27986652, -3.64532398, -1.28635204, -2.42362875,
0.01107288, -2.53222176, -2.0886136 , -5.54047694, -2.18389607,
-1.11665628, -3.07161217, -2.06070336, -0.84464262, 1.29238438,
-0.64973999, -2.63805504, -3.93317576, 0.65546645, 2.24721181,
-0.73403676, 5.31628298, -1.2208384 , 4.77782252, -1.42978168,
-3.3089274 , 3.25370494, 3.02117591, -1.54862932, -1.07360811,
1.2004856 , -4.3017773 , -4.95787789, -1.95245901, -2.15960839,
-3.78592731, -1.74096185, 3.54891595, 0.56294143, 1.15288455,
-0.77323696, 2.34430694, -1.05302007, -0.7514684 , -0.98321063,
-3.01300144, -3.00033274, 0.44200837, 0.45060886, -1.84497318,
-1.89616746, -2.15647664, -2.65672581, -3.65493379, 1.70923375,
-3.88695218, -0.05151283, 4.51906677, -2.28117003, 3.03032793,
-1.47713194, -0.35625273, 3.73501587, -2.09328047, -0.60665614,
-0.78177188, -0.67298545, 2.97436033, -0.29407932, 2.98482427,
-1.54951178, 2.79206821, 4.2225733 , 2.56265198, 2.80373284])>}
log_prob of sample: -194.96442183797524
Optimisons maintenant pour trouver les valeurs des paramètres avec la probabilité postérieure la plus élevée. Nous allons définir une variable pour chaque paramètre et contraindre leurs valeurs à être positives.
# Create the trainable model parameters, which we'll subsequently optimize.
# Note that we constrain them to be strictly positive.
constrain_positive = tfb.Shift(np.finfo(np.float64).tiny)(tfb.Exp())
amplitude_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='amplitude',
dtype=np.float64)
length_scale_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='length_scale',
dtype=np.float64)
observation_noise_variance_var = tfp.util.TransformedVariable(
initial_value=1.,
bijector=constrain_positive,
name='observation_noise_variance_var',
dtype=np.float64)
trainable_variables = [v.trainable_variables[0] for v in
[amplitude_var,
length_scale_var,
observation_noise_variance_var]]
Pour conditionner le modèle sur nos données observées, nous allons définir une target_log_prob fonction, qui prend les hyperparamètres du noyau (encore être inférées).
def target_log_prob(amplitude, length_scale, observation_noise_variance):
return gp_joint_model.log_prob({
'amplitude': amplitude,
'length_scale': length_scale,
'observation_noise_variance': observation_noise_variance,
'observations': observations_
})
# Now we optimize the model parameters.
num_iters = 1000
optimizer = tf.optimizers.Adam(learning_rate=.01)
# Use `tf.function` to trace the loss for more efficient evaluation.
@tf.function(autograph=False, jit_compile=False)
def train_model():
with tf.GradientTape() as tape:
loss = -target_log_prob(amplitude_var, length_scale_var,
observation_noise_variance_var)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
# Store the likelihood values during training, so we can plot the progress
lls_ = np.zeros(num_iters, np.float64)
for i in range(num_iters):
loss = train_model()
lls_[i] = loss
print('Trained parameters:')
print('amplitude: {}'.format(amplitude_var._value().numpy()))
print('length_scale: {}'.format(length_scale_var._value().numpy()))
print('observation_noise_variance: {}'.format(observation_noise_variance_var._value().numpy()))
Trained parameters: amplitude: 0.9176153445125278 length_scale: 0.18444082442910079 observation_noise_variance: 0.0880273312850989
# Plot the loss evolution
plt.figure(figsize=(12, 4))
plt.plot(lls_)
plt.xlabel("Training iteration")
plt.ylabel("Log marginal likelihood")
plt.show()

# Having trained the model, we'd like to sample from the posterior conditioned
# on observations. We'd like the samples to be at points other than the training
# inputs.
predictive_index_points_ = np.linspace(-1.2, 1.2, 200, dtype=np.float64)
# Reshape to [200, 1] -- 1 is the dimensionality of the feature space.
predictive_index_points_ = predictive_index_points_[..., np.newaxis]
optimized_kernel = tfk.ExponentiatedQuadratic(amplitude_var, length_scale_var)
gprm = tfd.GaussianProcessRegressionModel(
kernel=optimized_kernel,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_var,
predictive_noise_variance=0.)
# Create op to draw 50 independent samples, each of which is a *joint* draw
# from the posterior at the predictive_index_points_. Since we have 200 input
# locations as defined above, this posterior distribution over corresponding
# function values is a 200-dimensional multivariate Gaussian distribution!
num_samples = 50
samples = gprm.sample(num_samples)
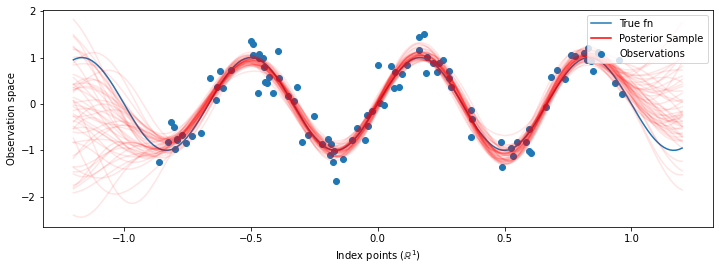
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
Marginalisation des hyperparamètres avec HMC
Au lieu d'optimiser les hyperparamètres, essayons de les intégrer avec l'hamiltonien Monte Carlo. Nous allons d'abord définir et exécuter un échantillonneur pour tirer approximativement de la distribution postérieure sur les hyperparamètres du noyau, compte tenu des observations.
num_results = 100
num_burnin_steps = 50
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob,
step_size=tf.cast(0.1, tf.float64)),
bijector=[constrain_positive, constrain_positive, constrain_positive])
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=tf.cast(0.75, tf.float64))
initial_state = [tf.cast(x, tf.float64) for x in [1., 1., 1.]]
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=False)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=lambda current_state, kernel_results: kernel_results)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 9.00s.
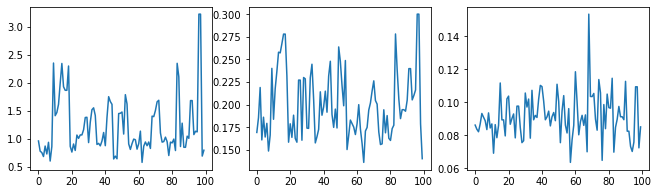
Vérifions l'intégrité de l'échantillonneur en examinant les traces d'hyperparamètres.
(amplitude_samples,
length_scale_samples,
observation_noise_variance_samples) = samples
f = plt.figure(figsize=[15, 3])
for i, s in enumerate(samples):
ax = f.add_subplot(1, len(samples) + 1, i + 1)
ax.plot(s)
Maintenant , au lieu de construire un seul GP avec les hyperparamètres optimisés, on construit la distribution prédictive a posteriori comme un mélange de médecins généralistes , chacun étant défini par un échantillon de la distribution postérieure sur hyperparam'etres. Cela s'intègre approximativement sur les paramètres postérieurs via un échantillonnage de Monte Carlo pour calculer la distribution prédictive marginale aux emplacements non observés.
# The sampled hyperparams have a leading batch dimension, `[num_results, ...]`,
# so they construct a *batch* of kernels.
batch_of_posterior_kernels = tfk.ExponentiatedQuadratic(
amplitude_samples, length_scale_samples)
# The batch of kernels creates a batch of GP predictive models, one for each
# posterior sample.
batch_gprm = tfd.GaussianProcessRegressionModel(
kernel=batch_of_posterior_kernels,
index_points=predictive_index_points_,
observation_index_points=observation_index_points_,
observations=observations_,
observation_noise_variance=observation_noise_variance_samples,
predictive_noise_variance=0.)
# To construct the marginal predictive distribution, we average with uniform
# weight over the posterior samples.
predictive_gprm = tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(logits=tf.zeros([num_results])),
components_distribution=batch_gprm)
num_samples = 50
samples = predictive_gprm.sample(num_samples)
# Plot the true function, observations, and posterior samples.
plt.figure(figsize=(12, 4))
plt.plot(predictive_index_points_, sinusoid(predictive_index_points_),
label='True fn')
plt.scatter(observation_index_points_[:, 0], observations_,
label='Observations')
for i in range(num_samples):
plt.plot(predictive_index_points_, samples[i, :], c='r', alpha=.1,
label='Posterior Sample' if i == 0 else None)
leg = plt.legend(loc='upper right')
for lh in leg.legendHandles:
lh.set_alpha(1)
plt.xlabel(r"Index points ($\mathbb{R}^1$)")
plt.ylabel("Observation space")
plt.show()
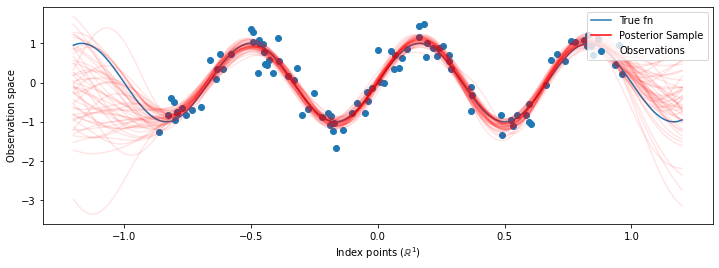
Bien que les différences soient subtiles dans ce cas, en général, nous nous attendrions à ce que la distribution prédictive postérieure se généralise mieux (donne une probabilité plus élevée aux données conservées) que d'utiliser simplement les paramètres les plus probables comme nous l'avons fait ci-dessus.
