 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
Các mô hình biến tiềm ẩn cố gắng nắm bắt cấu trúc ẩn trong dữ liệu chiều cao. Các ví dụ bao gồm phân tích thành phần nguyên tắc (PCA) và phân tích nhân tố. Các quy trình Gaussian là các mô hình "phi tham số" có thể linh hoạt nắm bắt cấu trúc tương quan cục bộ và độ không đảm bảo. Quá trình Gaussian tiềm ẩn biến mô hình ( Lawrence, 2004 ) kết hợp những khái niệm này.
Bối cảnh: Quy trình Gaussian
Quá trình Gaussian là bất kỳ tập hợp các biến ngẫu nhiên nào sao cho phân phối biên trên bất kỳ tập hợp con hữu hạn nào là phân phối chuẩn đa biến. Đối với một cái nhìn chi tiết tại các bác sĩ trong bối cảnh suy thoái, hãy kiểm tra Gaussian Process Regression trong TensorFlow Xác suất .
Chúng tôi sử dụng một bộ chỉ số cái gọi là nhãn mỗi của các biến ngẫu nhiên trong bộ sưu tập mà bao gồm GP. Trong trường hợp một tập chỉ số hữu hạn, chúng ta chỉ nhận được một chuẩn tắc đa biến. GP là thú vị nhất, tuy nhiên, khi chúng ta xem xét các bộ sưu tập vô hạn. Trong trường hợp của bộ chỉ số như \(\mathbb{R}^D\), nơi chúng tôi có một biến ngẫu nhiên cho tất cả các điểm trong \(D\)không gian ba chiều, bác sĩ gia đình có thể được coi như là một bản phân phối qua chức năng ngẫu nhiên. Một trận hòa duy nhất từ một GP như vậy, nếu nó có thể được thực hiện, sẽ gán một giá trị (cùng thường phân phối) để mọi điểm trong \(\mathbb{R}^D\). Trong colab này, chúng tôi sẽ tập trung vào GP của trên một số\(\mathbb{R}^D\).
Phân phối chuẩn hoàn toàn được xác định bởi thống kê bậc nhất và bậc hai của chúng - thực sự, một cách để xác định phân phối chuẩn là một cách có tích lũy bậc cao hơn của chúng đều bằng không. Đây là trường hợp cho GP, quá: chúng ta hoàn toàn xác định một GP bằng cách mô tả * trung bình và hiệp phương sai. Nhớ lại rằng đối với chuẩn tắc đa biến hữu hạn chiều, giá trị trung bình là một vectơ và hiệp phương sai là một ma trận xác định dương đối xứng, vuông. Trong GP vô hạn chiều, những cấu trúc khái quát để một chức năng bình \(m : \mathbb{R}^D \to \mathbb{R}\), quy định tại mỗi điểm của tập chỉ số, và một hiệp phương sai "hạt nhân" chức năng,\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). Chức năng hạt nhân bắt buộc phải tích cực-rõ ràng , trong đó chủ yếu nói rằng, giới hạn trong một tập hữu hạn các điểm, nó mang lại một ma trận postiive-định.
Hầu hết cấu trúc của một GP bắt nguồn từ hàm nhân hiệp phương sai của nó - hàm này mô tả các giá trị của hàm sampeld khác nhau như thế nào trên các điểm lân cận (hoặc không gần). Các hàm hiệp phương sai khác nhau khuyến khích các mức độ mượt mà khác nhau. Một chức năng hạt nhân thường được sử dụng là "exponentiated bậc hai" (aka "gaussian", "bình hàm mũ" hoặc "hàm cơ sở xuyên tâm"), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). Những ví dụ khác được nêu trên David Duvenaud của trang kernel sách dạy nấu ăn , cũng như trong các văn bản kinh điển Processes Gaussian cho Machine Learning .
* Với tập chỉ số vô hạn, chúng ta cũng yêu cầu một điều kiện nhất quán. Vì định nghĩa của GP là về các biên hữu hạn, chúng ta phải yêu cầu rằng các biên này phải nhất quán bất kể thứ tự mà các biên được lấy. Đây là một chủ đề hơi nâng cao trong lý thuyết về các quy trình ngẫu nhiên, nằm ngoài phạm vi của hướng dẫn này; đủ để nói rằng mọi thứ cuối cùng vẫn diễn ra tốt đẹp!
Áp dụng GPs: Mô hình hồi quy và biến tiềm ẩn
Một cách chúng ta có thể sử dụng GPS cho hồi quy: cho một loạt các dữ liệu quan sát được trong các hình thức đầu vào \(\{x_i\}_{i=1}^N\) (yếu tố của bộ index) và quan sát\(\{y_i\}_{i=1}^N\), chúng ta có thể sử dụng chúng để tạo thành một phân phối dự đoán sau tại một mới tập hợp các điểm \(\{x_j^*\}_{j=1}^M\). Kể từ khi các bản phân phối đều Gaussian, này nắm để một số đại số tuyến tính đơn giản (nhưng lưu ý: các tính toán cần thiết phải thực thi khối trong số các điểm dữ liệu và yêu cầu bậc hai không gian trong số các điểm dữ liệu - đây là một yếu tố hạn chế lớn trong việc sử dụng các bác sĩ đa khoa và nhiều nghiên cứu hiện tại tập trung vào các lựa chọn thay thế khả thi về mặt tính toán cho các suy luận sau chính xác). Chúng tôi bao gồm GP hồi quy chi tiết hơn trong các GP Regression trong TFP colab .
Một cách khác mà chúng ta có thể sử dụng GP là một mô hình biến tiềm ẩn: với một tập hợp các quan sát chiều cao (ví dụ: hình ảnh), chúng ta có thể xác định một số cấu trúc tiềm ẩn chiều thấp. Chúng tôi giả định rằng, có điều kiện về cấu trúc tiềm ẩn, số lượng lớn các kết quả đầu ra (pixel trong hình ảnh) là độc lập với nhau. Đào tạo trong mô hình này bao gồm
- tối ưu hóa các tham số mô hình (tham số chức năng hạt nhân cũng như, ví dụ, phương sai nhiễu quan sát), và
- tìm kiếm, đối với mỗi quan sát huấn luyện (hình ảnh), một vị trí điểm tương ứng trong tập chỉ mục. Tất cả việc tối ưu hóa có thể được thực hiện bằng cách tối đa hóa khả năng ghi nhật ký biên của dữ liệu.
Nhập khẩu
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Tải dữ liệu MNIST
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
Chuẩn bị các biến có thể huấn luyện
Chúng ta sẽ cùng đào tạo 3 tham số mô hình cũng như các đầu vào tiềm ẩn.
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
Xây dựng mô hình và hoạt động đào tạo
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
Đào tạo và vẽ biểu đồ nhúng tiềm ẩn kết quả
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
Lô kết quả
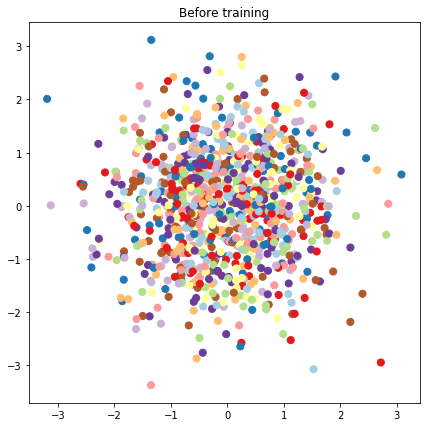
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
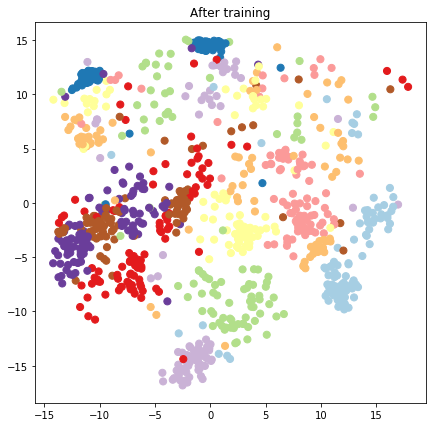
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
Xây dựng mô hình dự đoán và các hoạt động lấy mẫu
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
Vẽ các mẫu được điều chỉnh dựa trên dữ liệu và nhúng tiềm ẩn
Chúng tôi lấy mẫu ở 100 điểm trên lưới 2 chiều trong không gian tiềm ẩn.
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

Sự kết luận
Chúng tôi đã xem qua mô hình biến tiềm ẩn quá trình Gaussian và chỉ ra cách chúng tôi có thể triển khai nó chỉ trong một vài dòng mã TF và TF Probability.
