Aprenda o que há de mais recente em aprendizado de máquina, IA generativa e muito mais no WiML Symposium 2023 Registre-se

Esta página foi traduzida pela API Cloud Translation.

Modelos de Variáveis Latentes de Processo Gaussiano

Ver no TensorFlow.org

Executar no Google Colab

Ver fonte no GitHub

Baixar caderno

Os modelos de variáveis latentes tentam capturar a estrutura oculta em dados dimensionais elevados. Os exemplos incluem análise de componentes principais (PCA) e análise fatorial. Os processos gaussianos são modelos "não paramétricos" que podem captar com flexibilidade a estrutura de correlação local e a incerteza. A latente modelo variável de processo Gaussian ( Lawrence, 2004 ) combina esses conceitos.

Antecedentes: Processos Gaussianos

Um processo gaussiano é qualquer coleção de variáveis aleatórias de forma que a distribuição marginal sobre qualquer subconjunto finito seja uma distribuição normal multivariada. Para um olhar detalhado em GPs no contexto da regressão, veja Gaussian regressão do processo em TensorFlow Probabilidade .

Nós usamos um chamado conjunto de índices para rotular cada uma das variáveis aleatórias na coleção que os compreende GP. No caso de um conjunto de índices finitos, obtemos apenas uma normal multivariada. Do GP são mais interessantes, no entanto, quando consideramos conjuntos infinitos. No caso de conjuntos de índices como \(\mathbb{R}^D\), onde temos uma variável aleatória para cada ponto em \(D\)espaço dimensional, o GP pode ser pensado como uma distribuição mais funções aleatórias. Uma única tração de tais GP um, se pudesse ser realizado, se atribuir um valor (normalmente em conjunto com uma distribuição) para cada ponto no \(\mathbb{R}^D\). Neste colab, vamos nos concentrar em GP de mais alguns\(\mathbb{R}^D\).

As distribuições normais são completamente determinadas por suas estatísticas de primeira e segunda ordem - de fato, uma maneira de definir a distribuição normal é aquela cujos cumulantes de ordem superior são todos zero. Este é o caso de GP, demasiado: nós especificamos completamente um GP por descrever a ^* média e covariância. Lembre-se de que, para normais multivariadas de dimensão finita, a média é um vetor e a covariância é uma matriz quadrada simétrica positiva-definida. No GP infinito-dimensional, estas estruturas podem ser generalizadas para uma função significativo \(m : \mathbb{R}^D \to \mathbb{R}\), definida em cada ponto do índice conjunto, e uma função de covariância "Kernel",\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). A função de núcleo é necessária para ser definida positiva , que diz que, essencialmente, limitada a um conjunto finito de pontos, produz-se uma matriz postiive-definido.

A maior parte da estrutura de um GP deriva de sua função kernel de covariância - esta função descreve como os valores das funções de sampeld variam em pontos próximos (ou não tão próximos). Diferentes funções de covariância encorajam diferentes graus de suavidade. Uma função de kernel comumente usado é o "exponenciadas quadrática" (aka, "Gaussian", "quadrado exponencial" ou "função de base radial"), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). Outros exemplos são descritos na de David Duvenaud página kernel do livro de receitas , bem como no texto canônico Processos de Gauss para Machine Learning .

_{* Com um conjunto de índices infinitos, também exigimos uma condição de consistência. Uma vez que a definição do GP é em termos de marginais finitos, devemos exigir que esses marginais sejam consistentes, independentemente da ordem em que os marginais são tomados. Este é um tópico um tanto avançado na teoria de processos estocásticos, fora do escopo deste tutorial; basta dizer que as coisas acabam dando certo!}

Aplicando GPs: Modelos de Regressão e Variável Latente

Uma maneira de usar o GPS é de regressão: dado um bando de dados observados na forma de entradas \(\{x_i\}_{i=1}^N\) (elementos do conjunto de índices) e observações\(\{y_i\}_{i=1}^N\), que podem utilizá-los para formar uma distribuição preditivo posterior a uma nova conjunto de pontos \(\{x_j^*\}_{j=1}^M\). Desde as distribuições são todos Gaussian, isso se resume a alguns álgebra linear simples (mas nota: os cálculos necessários têm tempo de execução cúbico no número de pontos de dados e exigem quadrática espaço no número de pontos de dados - este é um grande fator limitante na o uso de GPs e muitas pesquisas atuais enfocam alternativas computacionalmente viáveis para inferência posterior exata). Cobrimos regressão GP em mais detalhes no GP de regressão em colab TFP .

Outra maneira pela qual podemos usar os GPs é como um modelo de variável latente: dada uma coleção de observações de dimensões elevadas (por exemplo, imagens), podemos postular alguma estrutura latente de baixa dimensão. Assumimos que, condicional à estrutura latente, o grande número de saídas (pixels na imagem) são independentes entre si. O treinamento neste modelo consiste em

otimizar os parâmetros do modelo (parâmetros de função do kernel, bem como, por exemplo, variação de ruído de observação), e
encontrar, para cada observação de treinamento (imagem), uma localização de ponto correspondente no conjunto de índice. Toda a otimização pode ser feita maximizando a probabilidade de log marginal dos dados.

Importações

import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline

Populating the interactive namespace from numpy and matplotlib

Carregar Dados MNIST

# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
11501568/11490434 [==============================] - 0s 0us/step

Prepare variáveis treináveis

Estaremos treinando conjuntamente 3 parâmetros do modelo, bem como as entradas latentes.

# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')

# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()

# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')

Construir modelo e operações de treinamento

# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps

def create_kernel():
  amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
  length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
  kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
  return kernel

def loss_fn():
  observation_noise_variance = tf.math.softplus(
      EPS + unconstrained_observation_noise)
  gp = tfd.GaussianProcess(
      kernel=create_kernel(),
      index_points=latent_index_points,
      observation_noise_variance=observation_noise_variance)
  log_probs = gp.log_prob(observations_, name='log_prob')
  return -tf.reduce_mean(log_probs)

trainable_variables = [unconstrained_amplitude,
                       unconstrained_length_scale,
                       unconstrained_observation_noise,
                       latent_index_points]

optimizer = tf.optimizers.Adam(learning_rate=1.0)

@tf.function(autograph=False, jit_compile=True)
def train_model():
  with tf.GradientTape() as tape:
    loss_value = loss_fn()
  grads = tape.gradient(loss_value, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss_value

Treine e plote os embeddings latentes resultantes

# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
  loss = train_model()
  lips[i] = latent_index_points.numpy()
  if i % log_interval == 0 or i + 1 == num_iters:
    print("Loss at step %d: %f" % (i, loss))

Loss at step 0: 1108.121688
Loss at step 20: -159.633761
Loss at step 40: -263.014394
Loss at step 60: -283.713056
Loss at step 80: -288.709413
Loss at step 99: -289.662253

Resultados do gráfico

# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
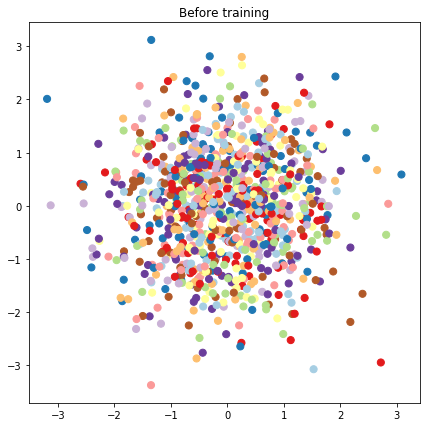
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
           c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()

plt.figure(figsize=(7, 7))
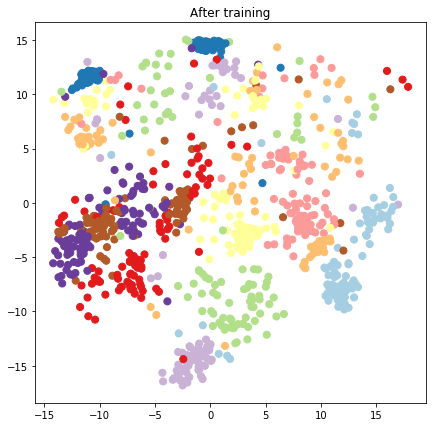
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
           c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()

png

Construir modelo preditivo e operações de amostragem

# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space. 
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)

# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
#   1. batch shape: [sample_grid_points, sample_grid_points, 1]
#   2. number of examples: [1]
#   3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)

# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
    kernel=create_kernel(),
    # Shape [10, 10, 1, 1, 2]
    index_points=grid_,
    # Shape [1000, 2]. 1000 2 dimensional vectors.
    observation_index_points=latent_index_points,
    # Shape [784, 1000]. A batch of 784 1000-dimensional observations.
    observations=observations_)

Desenhe amostras condicionadas aos dados e embeddings latentes

Amostramos em 100 pontos em uma grade 2-d no espaço latente.

samples = gprm.sample()

# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
             samples_.min(-1, keepdims=True)) /
            (samples_.max(-1, keepdims=True) -
             samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

png

Conclusão

Fizemos um breve tour pelo modelo de variável latente do processo gaussiano e mostramos como podemos implementá-lo em apenas algumas linhas de código de probabilidade TF e TF.

Modelos de Variáveis ​​Latentes de Processo Gaussiano