 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
Modele zmiennych utajonych próbują uchwycić ukrytą strukturę w danych wielowymiarowych. Przykłady obejmują analizę głównych składników (PCA) i analizę czynnikową. Procesy Gaussa są modelami „nieparametrycznymi”, które mogą elastycznie uchwycić lokalną strukturę korelacji i niepewność. Proces Gaussa utajony modelu zmienna ( Lawrence, 2004 ) łączy te koncepcje.
Tło: Procesy Gaussa
Proces Gaussa to dowolny zbiór zmiennych losowych, taki, że rozkład krańcowy w dowolnym skończonym podzbiorze jest wielowymiarowym rozkładem normalnym. Aby uzyskać szczegółowe spojrzenie na GPS w kontekście regresji, sprawdź Gaussa Process regres TensorFlow prawdopodobieństwa .
Używamy tzw zestaw do oznaczania indeksu każdej ze zmiennych losowych w zbiorach że obejmuje GP. W przypadku zbioru indeksów skończonych otrzymujemy po prostu wielowymiarową normalną. GP są najbardziej interesujące, chociaż, jeśli weźmiemy pod uwagę nieskończone zbiory. W przypadku zbiorów indeksowych jak \(\mathbb{R}^D\), gdzie mamy zmienną losową dla każdego punktu w \(D\)-wymiarowej przestrzeni, GP może być uważany za dystrybucję ponad losowych funkcji. Jeden remis z takiego lekarza, czy może to być zrealizowane, by przypisać wartość (wspólnie normalnie dostarczana) do każdego punktu w \(\mathbb{R}^D\). W tym colab, skupimy się na GPS nad jakimś\(\mathbb{R}^D\).
Rozkłady normalne są całkowicie określone przez ich statystyki pierwszego i drugiego rzędu — w rzeczywistości jednym ze sposobów zdefiniowania rozkładu normalnego jest taki, którego kumulanty wyższego rzędu wynoszą zero. Jest to przypadek dla GPS, zbyt: jesteśmy całkowicie określić GP opisując średniej i kowariancji *. Przypomnijmy, że dla skończonych wymiarów wielowymiarowych normalnych, średnia jest wektorem, a kowariancja jest kwadratową, symetryczną macierzą dodatnio określoną. W GP nieskończonej-wymiarowej, struktury te uogólniać do średniej funkcji \(m : \mathbb{R}^D \to \mathbb{R}\), zdefiniowanej w każdym punkcie zbioru indeksów i funkcji kowariancji „jądra”,\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). Funkcja jądra muszą być pozytywne, zdecydowany , który zasadniczo mówi, że ogranicza się do skończonego zbioru punktów, to daje macierz postiive-definitywna.
Większość struktury GP wywodzi się z funkcji jądra kowariancji — ta funkcja opisuje, w jaki sposób wartości funkcji próbkowania różnią się w pobliskich (lub nie tak bliskich) punktach. Różne funkcje kowariancji zachęcają do różnych stopni gładkości. Jednym z powszechnie stosowanych funkcji jądra jest „potęgowania kwadratowa” (aka „Gaussa”, „kwadrat wykładniczy” lub „radialna funkcja bazowa”), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). Inne przykłady są przedstawione na Davida Duvenaud na stronie książki kucharskiej jądra , a także w kanonicznych tekstów Gaussa procesów uczenia maszynowego .
* W przypadku zestawu indeksów nieskończonych wymagamy również warunku spójności. Ponieważ definicja GP jest w kategoriach skończonych marginesów, musimy wymagać, aby te brzegi były spójne, niezależnie od kolejności, w jakiej marginesy są brane. Jest to nieco zaawansowany temat w teorii procesów stochastycznych, poza zakresem tego samouczka; wystarczy powiedzieć, że w końcu wszystko się układa!
Stosowanie lekarzy rodzinnych: modele regresji i utajonych zmiennych
Jednym ze sposobów, możemy użyć GPS jest dla regresji: podany grono zaobserwowanych danych w postaci wejść \(\{x_i\}_{i=1}^N\) (elementy zestawu INDEX) i obserwacji\(\{y_i\}_{i=1}^N\), możemy wykorzystać do utworzenia tylną dystrybucję predykcyjnego w nowej zbiór punktów \(\{x_j^*\}_{j=1}^M\). Ponieważ są wszystkie dystrybucje Gaussa, to sprowadza się do jakiegoś prostego algebry liniowej (ale uwaga: wymagane obliczenia mają Runtime sześcienny liczby punktów danych i wymagają przestrzeni kwadratowego liczby punktów danych - to jest głównym czynnikiem ograniczającym korzystanie z lekarzy rodzinnych i wiele aktualnych badań koncentruje się na obliczeniowo wykonalnych alternatywach dla dokładnego wnioskowania a posteriori). Zajmujemy regresji GP bardziej szczegółowo w GP regres TFP colab .
Innym sposobem, w jaki możemy używać GP jest jako model zmiennej ukrytej: mając zbiór obserwacji wielowymiarowych (np. obrazów), możemy postawić jakąś niskowymiarową strukturę utajoną. Zakładamy, że w zależności od struktury ukrytej, duża liczba wyjść (pikseli na obrazie) jest od siebie niezależna. Szkolenie w tym modelu składa się z
- optymalizacja parametrów modelu (parametry funkcji jądra oraz np. wariancji szumu obserwacji), oraz
- znalezienie dla każdej obserwacji treningowej (obrazu) odpowiedniej lokalizacji punktu w zbiorze indeksów. Całą optymalizację można wykonać, maksymalizując marginalne prawdopodobieństwo logarytmiczne danych.
Import
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Załaduj dane MNIST
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
Przygotuj zmienne, które można trenować
Będziemy wspólnie trenować 3 parametry modelu, a także ukryte dane wejściowe.
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
Skonstruuj model i operacje szkoleniowe
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
Trenuj i rysuj powstałe ukryte osadzania
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
Wykres wyników
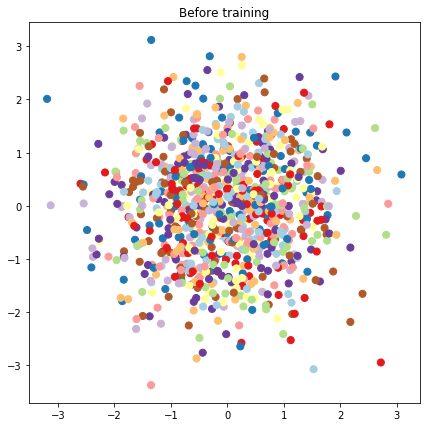
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
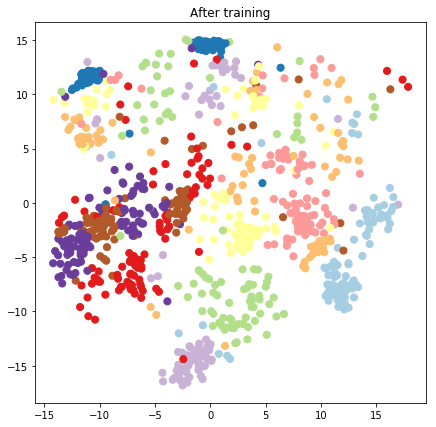
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
Skonstruuj model predykcyjny i operacje próbkowania
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
Narysuj próbki uzależnione od danych i ukrytych osadzeń
Próbkujemy w 100 punktach na siatce dwuwymiarowej w przestrzeni utajonej.
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

Wniosek
Odbyliśmy krótką prezentację modelu zmiennej ukrytej procesu Gaussa i pokazaliśmy, jak możemy go zaimplementować w zaledwie kilku wierszach kodu prawdopodobieństwa TF i TF.
