 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
Model variabel laten mencoba menangkap struktur tersembunyi dalam data berdimensi tinggi. Contohnya termasuk analisis komponen prinsip (PCA) dan analisis faktor. Proses Gaussian adalah model "non-parametrik" yang dapat secara fleksibel menangkap struktur korelasi lokal dan ketidakpastian. Proses Gaussian laten variabel Model ( Lawrence, 2004 ) menggabungkan konsep-konsep ini.
Latar Belakang: Proses Gaussian
Proses Gaussian adalah setiap kumpulan variabel acak sedemikian rupa sehingga distribusi marjinal atas setiap subset hingga adalah distribusi normal multivariat. Untuk melihat rinci pada dokter dalam konteks regresi, periksa Gaussian Proses Regresi di TensorFlow Probabilitas .
Kami menggunakan apa yang disebut indeks set untuk label setiap variabel acak dalam koleksi yang terdiri GP. Dalam kasus set indeks yang terbatas, kami hanya mendapatkan normal multivariat. GP yang paling menarik, meskipun, ketika kita mempertimbangkan koleksi yang tak terbatas. Dalam kasus indeks set seperti \(\mathbb{R}^D\), di mana kita memiliki variabel acak untuk setiap titik di \(D\)ruang berdimensi, GP dapat dianggap sebagai distribusi melalui fungsi acak. Hasil imbang tunggal dari dokter umum tersebut, jika bisa direalisasikan, akan menetapkan (bersama-sama biasanya didistribusikan) nilai setiap titik di \(\mathbb{R}^D\). Dalam colab ini, kita akan fokus pada GP atas beberapa\(\mathbb{R}^D\).
Distribusi normal sepenuhnya ditentukan oleh statistik orde pertama dan kedua -- memang, salah satu cara untuk mendefinisikan distribusi normal adalah sebagai distribusi yang kumulan orde tingginya semuanya nol. Ini adalah kasus untuk GP, juga: kita benar-benar menentukan GP dengan menggambarkan mean dan kovariansi *. Ingatlah bahwa untuk normal multivariat berdimensi-hingga, rata-ratanya adalah vektor dan kovariansnya adalah matriks bujursangkar positif-pasti yang simetris. Dalam GP dimensi tak terbatas, struktur ini menggeneralisasi ke fungsi berarti \(m : \mathbb{R}^D \to \mathbb{R}\), pasti pada setiap titik dari indeks set, dan kovarians fungsi "kernel",\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). Fungsi kernel diperlukan untuk menjadi positif-yang pasti , yang pada dasarnya mengatakan bahwa, terbatas pada satu set terbatas poin, ia menghasilkan matriks postiive-pasti.
Sebagian besar struktur GP berasal dari fungsi kernel kovariansnya -- fungsi ini menjelaskan bagaimana nilai fungsi sampel bervariasi di titik terdekat (atau tidak terlalu dekat). Fungsi kovarians yang berbeda mendorong tingkat kehalusan yang berbeda. Salah satu fungsi kernel yang umum digunakan adalah "exponentiated kuadrat" (alias, "gaussian", "kuadrat eksponensial" atau "radial basis function"), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). Contoh lain diuraikan pada David Duvenaud ini halaman kernel masak , serta dalam teks kanonik Proses Gaussian untuk Machine Learning .
* Dengan set indeks tak terbatas, kami juga membutuhkan kondisi konsistensi. Karena definisi GP adalah dalam hal marjinal hingga, kita harus mensyaratkan bahwa marjinal ini konsisten terlepas dari urutan pengambilan marjinal. Ini adalah topik yang agak maju dalam teori proses stokastik, di luar cakupan tutorial ini; cukuplah untuk mengatakan bahwa semuanya berjalan baik-baik saja pada akhirnya!
Menerapkan GP: Model Variabel Regresi dan Laten
Salah satu cara kita dapat menggunakan dokter adalah untuk regresi: diberikan sekelompok data yang diamati dalam bentuk masukan \(\{x_i\}_{i=1}^N\) (unsur indeks set) dan pengamatan\(\{y_i\}_{i=1}^N\), kita dapat menggunakan ini untuk membentuk distribusi prediksi posterior pada baru set poin \(\{x_j^*\}_{j=1}^M\). Karena distribusi semua Gaussian, ini bermuara pada beberapa aljabar linier sederhana (tapi catatan: perhitungan diperlukan memiliki runtime kubik dalam jumlah titik data dan membutuhkan ruang kuadrat dalam jumlah titik data - ini adalah faktor pembatas utama dalam penggunaan dokter umum dan banyak penelitian saat ini berfokus pada alternatif komputasi yang layak untuk inferensi posterior yang tepat). Kami mencakup GP regresi secara lebih rinci di GP Regresi di TFP colab .
Cara lain kita dapat menggunakan GP adalah sebagai model variabel laten: diberikan koleksi pengamatan dimensi tinggi (misalnya, gambar), kita dapat menempatkan beberapa struktur laten dimensi rendah. Kami berasumsi bahwa, tergantung pada struktur laten, sejumlah besar output (piksel dalam gambar) tidak tergantung satu sama lain. Pelatihan dalam model ini terdiri dari
- mengoptimalkan parameter model (parameter fungsi kernel serta, misalnya, varians noise observasi), dan
- menemukan, untuk setiap pengamatan pelatihan (gambar), lokasi titik yang sesuai dalam kumpulan indeks. Semua optimasi dapat dilakukan dengan memaksimalkan kemungkinan log marginal dari data.
Impor
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Muat Data MNIST
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
Siapkan variabel yang bisa dilatih
Kami akan bersama-sama melatih 3 parameter model serta input laten.
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
Membangun model dan pelatihan ops
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
Latih dan plot hasil penyematan laten
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
Hasil plot
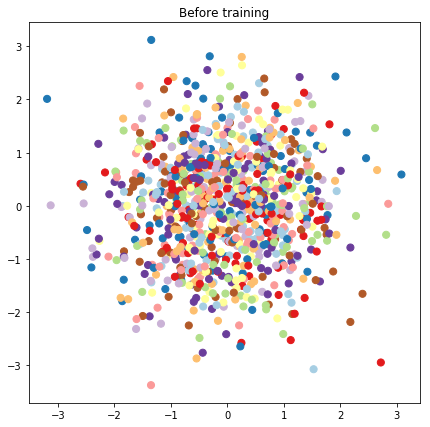
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
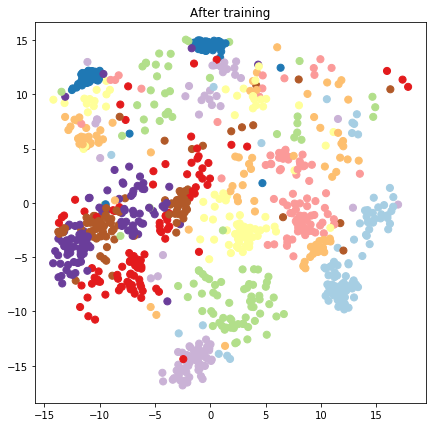
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
Bangun model prediktif dan operasi pengambilan sampel
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
Gambarkan sampel yang dikondisikan pada data dan penyematan laten
Kami mengambil sampel pada 100 titik pada kisi 2-d di ruang laten.
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

Kesimpulan
Kami telah mengikuti tur singkat model variabel laten proses Gaussian, dan menunjukkan bagaimana kami dapat mengimplementasikannya hanya dalam beberapa baris kode TF dan Probabilitas TF.
