مدلهای متغیر نهفته فرآیند گاوسی

مشاهده در TensorFlow.org

در Google Colab اجرا شود

مشاهده منبع در GitHub

دانلود دفترچه یادداشت

مدل‌های متغیر پنهان تلاش می‌کنند تا ساختار پنهان را در داده‌های با ابعاد بالا ثبت کنند. به عنوان مثال می توان به تحلیل مؤلفه های اصلی (PCA) و تحلیل عاملی اشاره کرد. فرآیندهای گاوسی مدل‌های «ناپارامتریک» هستند که می‌توانند ساختار همبستگی محلی و عدم قطعیت را به‌طور انعطاف‌پذیر ثبت کنند. فرآیند گاوسی مدل متغیر مکنون ( لارنس، 2004 ) ترکیبی از این مفاهیم.

زمینه: فرآیندهای گاوسی

فرآیند گاوسی هر مجموعه ای از متغیرهای تصادفی است به طوری که توزیع حاشیه ای بر روی هر زیر مجموعه محدود یک توزیع نرمال چند متغیره است. برای یک نگاه دقیق در پزشکان در زمینه رگرسیون، چک کردن رگرسیون فرآیند گاوسی در احتمال TensorFlow .

ما با استفاده از یک به اصطلاح مجموعه ای شاخص به برچسب هر یک از متغیرهای تصادفی در مجموعه که شامل GP است. در مورد یک مجموعه شاخص محدود، فقط یک نرمال چند متغیره بدست می آوریم. در GP جالب ترین هستند، هر چند، هنگامی که ما مجموعه های نامحدود در نظر بگیرید. در مورد مجموعه شاخص مانند \(\mathbb{R}^D\)، که در آن ما یک متغیر تصادفی برای هر نقطه در \(D\)فضای بعدی، پزشک عمومی می تواند به عنوان یک توزیع بیش از توابع تصادفی فکر می کردم. قرعه کشی تنها از چنین GP، اگر آن را می توان متوجه شد، یک (به طور مشترک به طور معمول توزیع شده) ارزش را به هر نقطه در اختصاص \(\mathbb{R}^D\). در این COLAB، ما در را GP بیش از برخی از تمرکز\(\mathbb{R}^D\).

توزیع های نرمال به طور کامل توسط آمار مرتبه اول و دوم آنها تعیین می شود - در واقع، یکی از راه های تعریف توزیع نرمال، توزیعی است که انباشته های مرتبه بالاتر آن همه صفر هستند. این مورد برای است GP، بیش از حد: ما به طور کامل یک پزشک عمومی با توصیف میانگین و کواریانس ^* مشخص کنید. به یاد بیاورید که برای نرمال های چند متغیره محدود، میانگین یک بردار و کوواریانس یک ماتریس مربع و متقارن مثبت-معین است. در GP بی نهایت بعدی، این سازه ها تعمیم به متوسط عملکرد \(m : \mathbb{R}^D \to \mathbb{R}\)، تعریف شده در هر نقطه از مجموعه شاخص، و یک کوواریانس "هسته" تابع،\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). تابع کرنل مورد نیاز است که مثبت قطعی ، که اساسا می گوید که، محدود به یک مجموعه متناهی از نقاط این عدد برابر یک ماتریس postiive-قطعی.

بیشتر ساختار یک GP از تابع هسته کوواریانس آن ناشی می شود -- این تابع چگونگی تغییر مقادیر توابع نمونه برداری در نقاط نزدیک (یا نه چندان نزدیک) را توصیف می کند. توابع کوواریانس مختلف درجات مختلف صافی را تشویق می کنند. یک تابع کرنل معمول مورد استفاده است که "exponentiated درجه دوم" (با نام مستعار "گاوسی"، "مربع نمایی" یا "تابع پایه شعاعی")، \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). نمونه های دیگر در دیوید Duvenaud را مشخص صفحه کتاب آشپزی هسته همانطور که در متن متعارف، و همچنین فرآیندهای گاوسی برای یادگیری ماشین .

_{* با مجموعه شاخص بی نهایت، ما نیز به یک شرط سازگاری نیاز داریم. از آنجایی که تعریف GP بر حسب حاشیه‌های محدود است، باید بخواهیم که این حاشیه‌ها صرف نظر از ترتیبی که حاشیه‌ها گرفته می‌شوند، سازگار باشند. این یک مبحث تا حدودی پیشرفته در تئوری فرآیندهای تصادفی است که در این آموزش نمی گنجد. کافی است بگوییم همه چیز در نهایت خوب پیش می رود!}

به کارگیری پزشکان عمومی: مدل های رگرسیونی و متغیرهای پنهان

یکی از راه های ما می توانید GPS استفاده برای رگرسیون: با توجه به یک دسته از داده های مشاهده شده در قالب ورودی \(\{x_i\}_{i=1}^N\) (عناصر مجموعه ای شاخص) و مشاهدات\(\{y_i\}_{i=1}^N\)، ما می توانیم این را به شکل یک توزیع پیش بینی خلفی در یک جدید استفاده کنید مجموعه ای از نقاط \(\{x_j^*\}_{j=1}^M\). از آنجا که توزیع گاوسی همه، این جوش پایین به برخی جبر خطی ساده (اما توجه داشته باشید: محاسبات لازم را در زمان اجرا در تعداد نقاط داده مکعب و نیاز به درجه دوم فضا در تعدادی از نقاط داده - این یک عامل محدود کننده اصلی در است استفاده از پزشکان عمومی و بسیاری از تحقیقات فعلی بر جایگزین های محاسباتی قابل دوام برای استنتاج دقیق پسین تمرکز دارد. ما را پوشش رگرسیون GP در جزئیات بیشتری را در رگرسیون GP در COLAB TFP .

راه دیگری که می‌توانیم از GPs استفاده کنیم، به‌عنوان یک مدل متغیر پنهان است: با توجه به مجموعه‌ای از مشاهدات با ابعاد بالا (مثلاً تصاویر)، می‌توانیم ساختار پنهانی با ابعاد پایین ارائه کنیم. ما فرض می کنیم که، مشروط به ساختار نهفته، تعداد زیادی خروجی (پیکسل ها در تصویر) مستقل از یکدیگر هستند. آموزش در این مدل شامل

1. بهینه سازی پارامترهای مدل (پارامترهای تابع هسته و همچنین، به عنوان مثال، واریانس نویز مشاهده)، و
2. پیدا کردن، برای هر مشاهده آموزشی (تصویر)، یک مکان نقطه مربوطه در مجموعه شاخص. تمام بهینه سازی را می توان با به حداکثر رساندن احتمال ورود به سیستم حاشیه ای داده ها انجام داد.

واردات

import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline

Populating the interactive namespace from numpy and matplotlib

داده های MNIST را بارگیری کنید

# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
11501568/11490434 [==============================] - 0s 0us/step

متغیرهای قابل آموزش را آماده کنید

ما به طور مشترک 3 پارامتر مدل و همچنین ورودی های پنهان را آموزش خواهیم داد.

# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')

# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()

# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')

ساخت مدل و عملیات آموزشی

# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps

def create_kernel():
  amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
  length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
  kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
  return kernel

def loss_fn():
  observation_noise_variance = tf.math.softplus(
      EPS + unconstrained_observation_noise)
  gp = tfd.GaussianProcess(
      kernel=create_kernel(),
      index_points=latent_index_points,
      observation_noise_variance=observation_noise_variance)
  log_probs = gp.log_prob(observations_, name='log_prob')
  return -tf.reduce_mean(log_probs)

trainable_variables = [unconstrained_amplitude,
                       unconstrained_length_scale,
                       unconstrained_observation_noise,
                       latent_index_points]

optimizer = tf.optimizers.Adam(learning_rate=1.0)

@tf.function(autograph=False, jit_compile=True)
def train_model():
  with tf.GradientTape() as tape:
    loss_value = loss_fn()
  grads = tape.gradient(loss_value, trainable_variables)
  optimizer.apply_gradients(zip(grads, trainable_variables))
  return loss_value

تعبیه های نهفته به دست آمده را آموزش و ترسیم کنید

# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
  loss = train_model()
  lips[i] = latent_index_points.numpy()
  if i % log_interval == 0 or i + 1 == num_iters:
    print("Loss at step %d: %f" % (i, loss))

Loss at step 0: 1108.121688
Loss at step 20: -159.633761
Loss at step 40: -263.014394
Loss at step 60: -283.713056
Loss at step 80: -288.709413
Loss at step 99: -289.662253

نتایج طرح

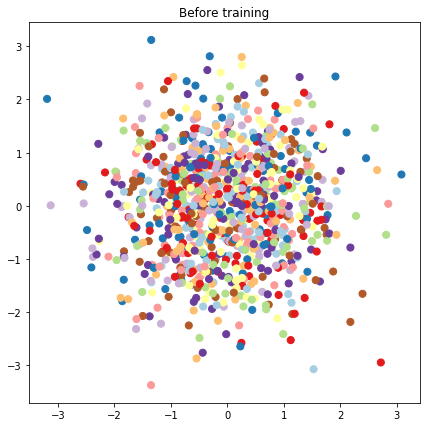
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
           c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()

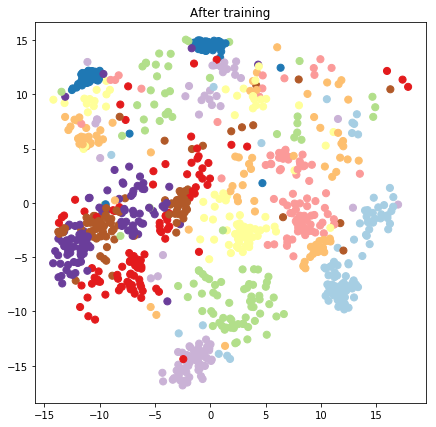
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
           c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()

مدل پیش‌بینی و نمونه‌برداری را بسازید

# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space. 
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)

# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
#   1. batch shape: [sample_grid_points, sample_grid_points, 1]
#   2. number of examples: [1]
#   3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)

# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
    kernel=create_kernel(),
    # Shape [10, 10, 1, 1, 2]
    index_points=grid_,
    # Shape [1000, 2]. 1000 2 dimensional vectors.
    observation_index_points=latent_index_points,
    # Shape [784, 1000]. A batch of 784 1000-dimensional observations.
    observations=observations_)

نمونه هایی را مشروط به داده ها و جاسازی های نهفته بکشید

ما در 100 نقطه در یک شبکه 2 بعدی در فضای پنهان نمونه برداری می کنیم.

samples = gprm.sample()

# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
             samples_.min(-1, keepdims=True)) /
            (samples_.max(-1, keepdims=True) -
             samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

نتیجه

ما یک تور مختصر از مدل متغیر نهفته فرآیند گاوسی گرفته‌ایم و نشان داده‌ایم که چگونه می‌توانیم آن را تنها در چند خط کد احتمال TF و TF پیاده‌سازی کنیم.