 Ver en TensorFlow.org Ver en TensorFlow.org |  Ejecutar en Google Colab Ejecutar en Google Colab |  Ver fuente en GitHub Ver fuente en GitHub |  Descargar cuaderno Descargar cuaderno |
Los modelos de variables latentes intentan capturar la estructura oculta en datos de alta dimensión. Los ejemplos incluyen análisis de componentes principales (PCA) y análisis factorial. Los procesos gaussianos son modelos "no paramétricos" que pueden capturar de manera flexible la estructura de correlación local y la incertidumbre. El proceso de Gauss latente modelo de variables ( Lawrence, 2004 ) combina estos conceptos.
Antecedentes: procesos gaussianos
Un proceso gaussiano es cualquier colección de variables aleatorias tal que la distribución marginal sobre cualquier subconjunto finito es una distribución normal multivariante. Para una visión detallada de los médicos en el contexto de la regresión, echa un vistazo a Gauss regresión de procesos en TensorFlow Probabilidad .
Utilizamos un llamado conjunto de índices para etiquetar cada una de las variables aleatorias en la colección que comprende los GP. En el caso de un conjunto de índices finito, obtenemos una normal multivariante. De GP son los más interesantes, sin embargo, cuando consideramos los conjuntos infinitos. En el caso de conjuntos de índices como \(\mathbb{R}^D\), donde tenemos una variable aleatoria para cada punto en \(D\)espacio dimensional, el médico de cabecera puede ser pensado como una distribución de las funciones aleatorias. Un único sorteo a partir de tal GP, si se podría realizar, sería asignar un valor (en conjunto distribuido normalmente) a cada punto en \(\mathbb{R}^D\). En este colab, nos centraremos en los médicos de familia sobre algunas\(\mathbb{R}^D\).
Las distribuciones normales están completamente determinadas por sus estadísticas de primer y segundo orden; de hecho, una forma de definir la distribución normal es aquella cuyos acumulados de orden superior son todos cero. Este es el caso de los médicos de familia, también: especificamos por completo un GP con la descripción de la media y la covarianza *. Recuerde que para las normales multivariadas de dimensión finita, la media es un vector y la covarianza es una matriz cuadrada, simétrica positiva definida. En el GP de dimensión infinita, estas estructuras generalizan a una función media \(m : \mathbb{R}^D \to \mathbb{R}\), definido en cada punto del conjunto de índices, y una función de covarianza "kernel",\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\). Se requiere que la función de núcleo para ser definida positiva , que dice esencialmente que, restringido a un conjunto finito de puntos, se produce una matriz postiive-definido.
La mayor parte de la estructura de un GP se deriva de su función de núcleo de covarianza: esta función describe cómo los valores de las funciones de muestra varían en puntos cercanos (o no tan cercanos). Las diferentes funciones de covarianza fomentan diferentes grados de suavidad. Una de las funciones del kernel utilizado es el de "a exponentes cuadrática" (también conocido como "gaussiana", "al cuadrado exponencial" o "función de base radial"), \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\). Otros ejemplos se describen en David Duvenaud página kernel libro de cocina , así como en los textos canónicos Procesos Gaussianos para aprendizaje automático .
* Con un conjunto de índices infinito, también requerimos una condición de coherencia. Dado que la definición de GP es en términos de marginales finitos, debemos exigir que estos marginales sean consistentes independientemente del orden en que se tomen los marginales. Este es un tema algo avanzado en la teoría de procesos estocásticos, fuera del alcance de este tutorial; ¡Basta decir que al final todo sale bien!
Aplicación de GP: regresión y modelos de variables latentes
Una forma de utilizar el GPS es para la regresión: dado un montón de datos observados en forma de entradas \(\{x_i\}_{i=1}^N\) (elementos del conjunto de índice) y observaciones\(\{y_i\}_{i=1}^N\), podemos utilizar estos para formar una distribución posterior predictiva en un nuevo conjunto de puntos \(\{x_j^*\}_{j=1}^M\). Dado que las distribuciones son todos de Gauss, esto se reduce a un poco de álgebra lineal simple (pero nota: los cálculos necesarios tener tiempo de ejecución cúbico en el número de puntos de datos y requieren cuadrática espacio en el número de puntos de datos - esto es un importante factor limitante en el uso de médicos de cabecera y gran parte de la investigación actual se centra en alternativas viables desde el punto de vista computacional a la inferencia posterior exacta). Cubrimos regresión GP con más detalle en el GP de regresión en colab PTF .
Otra forma en que podemos usar los GP es como un modelo de variable latente: dada una colección de observaciones de alta dimensión (por ejemplo, imágenes), podemos postular alguna estructura latente de baja dimensión. Suponemos que, condicionado a la estructura latente, la gran cantidad de salidas (píxeles en la imagen) son independientes entre sí. La formación en este modelo consiste en
- optimizar los parámetros del modelo (parámetros de la función del núcleo, así como, por ejemplo, la varianza del ruido de observación), y
- encontrar, para cada observación de entrenamiento (imagen), una ubicación de punto correspondiente en el conjunto de índices. Toda la optimización se puede realizar maximizando la probabilidad logarítmica marginal de los datos.
Importaciones
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Cargar datos MNIST
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
Preparar variables entrenables
Entrenaremos conjuntamente 3 parámetros del modelo, así como las entradas latentes.
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
Construir modelos y operaciones de entrenamiento
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
Entrene y trace las incrustaciones latentes resultantes
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
Trazar resultados
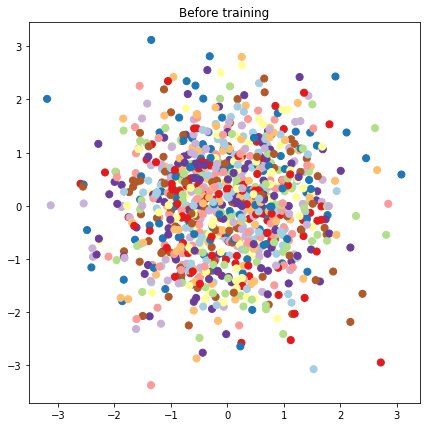
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
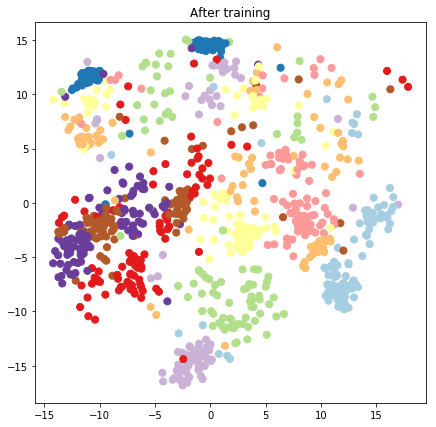
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
Construir modelos predictivos y operaciones de muestreo
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
Dibujar muestras condicionadas por los datos y las incrustaciones latentes
Tomamos muestras en 100 puntos en una cuadrícula de 2 d en el espacio latente.
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

Conclusión
Hemos realizado un breve recorrido por el modelo de variable latente del proceso gaussiano y hemos mostrado cómo podemos implementarlo en unas pocas líneas de código TF y TF Probability.
