 TensorFlow.org এ দেখুন TensorFlow.org এ দেখুন |  Google Colab-এ চালান Google Colab-এ চালান |  GitHub-এ উৎস দেখুন GitHub-এ উৎস দেখুন |  নোটবুক ডাউনলোড করুন নোটবুক ডাউনলোড করুন |
সুপ্ত পরিবর্তনশীল মডেলগুলি হাই ডাইমেনশনাল ডেটাতে লুকানো কাঠামো ক্যাপচার করার চেষ্টা করে। উদাহরণগুলির মধ্যে রয়েছে নীতি উপাদান বিশ্লেষণ (PCA) এবং ফ্যাক্টর বিশ্লেষণ। গাউসিয়ান প্রক্রিয়াগুলি হল "নন-প্যারামেট্রিক" মডেল যা নমনীয়ভাবে স্থানীয় পারস্পরিক সম্পর্ক কাঠামো এবং অনিশ্চয়তা ক্যাপচার করতে পারে। গসিয়ান প্রক্রিয়া সুপ্ত পরিবর্তনশীল মডেল ( লরেন্স, 2004 ) এই ধারণার সম্মিলন।
পটভূমি: গাউসিয়ান প্রসেস
একটি গাউসিয়ান প্রক্রিয়া হল র্যান্ডম ভেরিয়েবলের যেকোন সংগ্রহ যেমন যেকোন সীমিত উপসেটের উপর প্রান্তিক বন্টন হল একটি মাল্টিভ্যারিয়েট স্বাভাবিক বন্টন। রিগ্রেশন প্রেক্ষাপটে ইন জিপিএস হচ্ছে তা দেখাবে জন্য, খুজুন TensorFlow সম্ভবত গসিয়ান প্রক্রিয়া রিগ্রেশন ।
আমরা একটি তথাকথিত সূচক সেট ব্যবহার সংগ্রহে যে জিপি গঠিত র্যান্ডম ভেরিয়েবল প্রতিটি লেবেল। একটি সীমিত সূচক সেটের ক্ষেত্রে, আমরা কেবল একটি মাল্টিভেরিয়েট নরমাল পাই। গ্রামীণফোনের, সবচেয়ে আকর্ষণীয় যদিও আমরা যখন অসীম সংগ্রহের কথা বিবেচনা করুন। মত সূচক সেট যদি \(\mathbb{R}^D\), যেখানে আমরা প্রতিটি পয়েন্টের জন্য একটি এলোপাতাড়ি ভেরিয়েবলের আছে \(D\)-dimensional স্থান, জিপি র্যান্ডম ফাংশন উপর একটি ডিস্ট্রিবিউশন হিসেবে ভাবা যেতে পারে। যেমন একটি জিপি থেকে একটি একক ড্র, যদি এটা প্রতীত হতে পারে, প্রতিটি বিন্দু থেকে একটি (যৌথভাবে স্বাভাবিকভাবে বিতরণ) মান নির্ধারণ করবে \(\mathbb{R}^D\)। এই colab, আমরা কিছু উপর গ্রামীণফোনের মনোনিবেশ করব\(\mathbb{R}^D\)।
সাধারণ বন্টনগুলি সম্পূর্ণরূপে তাদের প্রথম এবং দ্বিতীয় ক্রম পরিসংখ্যান দ্বারা নির্ধারিত হয় -- প্রকৃতপক্ষে, স্বাভাবিক বন্টনকে সংজ্ঞায়িত করার একটি উপায় হল যার উচ্চ-ক্রম কিউমুল্যান্টগুলি সব শূন্য৷ এই গ্রামীণফোনের কেনার ক্ষেত্রে, অত্যধিক: আমরা সম্পূর্ণরূপে গড় এবং সহভেদাংক * বর্ণনা দ্বারা একটি জিপি উল্লেখ করুন। স্মরণ করুন যে সসীম-মাত্রিক মাল্টিভেরিয়েট স্বাভাবিকের জন্য, গড় হল একটি ভেক্টর এবং কোভেরিয়েন্স হল একটি বর্গক্ষেত্র, প্রতিসম ধনাত্মক-নির্দিষ্ট ম্যাট্রিক্স। অসীম-মাত্রিক জিপি, এই কাঠামো একটি গড় ফাংশন সাধারণের \(m : \mathbb{R}^D \to \mathbb{R}\)সূচক সেট প্রতিটি বিন্দুতে সংজ্ঞায়িত, এবং একটি সহভেদাংক "কার্নেল" ফাংশন,\(k : \mathbb{R}^D \times \mathbb{R}^D \to \mathbb{R}\)। কার্নেল ফাংশন হবে প্রয়োজন বোধ করা হয় ইতিবাচক-নির্দিষ্ট , যা মূলত যে বলছেন, পয়েন্ট একটি নির্দিষ্ট সেট অবধি সীমিত, এটি একটি postiive-নির্দিষ্ট ম্যাট্রিক্স উৎপাদ।
একটি জিপির বেশিরভাগ গঠনই এর কোভেরিয়েন্স কার্নেল ফাংশন থেকে উদ্ভূত হয় -- এই ফাংশনটি বর্ণনা করে যে কীভাবে নমুনা ফাংশনের মান কাছাকাছি (বা কাছাকাছি নয়) পয়েন্ট জুড়ে পরিবর্তিত হয়। বিভিন্ন কোভেরিয়েন্স ফাংশন বিভিন্ন মাত্রার মসৃণতাকে উৎসাহিত করে। এক সাধারণভাবে ব্যবহৃত কার্নেল ফাংশন "exponentiated দ্বিঘাত" (ওরফে, "গসিয়ান", বা "রশ্মীয় ভিত্তিতে ফাংশন" "সূচকীয় ছক"), হয় \(k(x, x') = \sigma^2 e^{(x - x^2) / \lambda^2}\)। অন্যান্য উদাহরণ ডেভিড Duvenaud এর উপর রূপরেখা আছে কার্নেল পাকপ্রণালীর পৃষ্ঠা ক্যানোনিকাল টেক্সট হিসেবে, পাশাপাশি মেশিন লার্নিং জন্য গসিয়ান প্রসেস ।
* একটি অসীম সূচক সেটের সাথে, আমাদের একটি সামঞ্জস্যের শর্তও প্রয়োজন। যেহেতু GP-এর সংজ্ঞাটি সীমিত প্রান্তিকের পরিপ্রেক্ষিতে, তাই আমাদের অবশ্যই প্রয়োজন হবে যে প্রান্তিকগুলি যে ক্রমে নেওয়া হোক না কেন এই প্রান্তিকগুলি সামঞ্জস্যপূর্ণ। এই টিউটোরিয়ালের সুযোগের বাইরে, স্টোকাস্টিক প্রক্রিয়ার তত্ত্বে এটি একটি কিছুটা উন্নত বিষয়; শেষ পর্যন্ত জিনিস ঠিক আছে বলার জন্য এটি যথেষ্ট!
জিপি প্রয়োগ করা: রিগ্রেশন এবং সুপ্ত পরিবর্তনশীল মডেল
ওয়ান ওয়ে আমরা GPS ব্যবহার করতে পারেন রিগ্রেশন জন্য: ইনপুট আকারে পর্যবেক্ষিত তথ্য একটি গুচ্ছ দেওয়া \(\{x_i\}_{i=1}^N\) (INDEX সেটের উপাদান) ও পর্যবেক্ষণের\(\{y_i\}_{i=1}^N\), আমরা এই একটি নতুন এ অবর ভবিষ্যদ্বাণীপূর্ণ বন্টন গঠন করতে ব্যবহার করতে পারেন পয়েন্ট সেট \(\{x_j^*\}_{j=1}^M\)। যেহেতু ডিস্ট্রিবিউশন সব গসিয়ান, এই কিছু সহজবোধ্য রৈখিক বীজগণিত নিচে boils (কিন্তু মনে রাখবেন: প্রয়োজনীয় কম্পিউটেশন ডাটা পয়েন্টের সংখ্যা রানটাইম কিউবিক আছে এবং ডাটা পয়েন্টের সংখ্যা স্থান দ্বিঘাত প্রয়োজন - এই একটি প্রধান সীমিত ফ্যাক্টর জিপি-এর ব্যবহার এবং বর্তমান গবেষণা সঠিক উত্তরের অনুমানের জন্য গণনামূলকভাবে কার্যকর বিকল্পগুলির উপর দৃষ্টি নিবদ্ধ করে)। আমরা আরো বিস্তারিত জিপি রিগ্রেশন আবরণ TFP colab জিপি রিগ্রেশন ।
আমরা GPs ব্যবহার করতে পারি আরেকটি উপায় হল একটি সুপ্ত পরিবর্তনশীল মডেল হিসাবে: উচ্চ-মাত্রিক পর্যবেক্ষণের (যেমন, ছবি) সংগ্রহ দেওয়া হলে, আমরা কিছু নিম্ন-মাত্রিক সুপ্ত কাঠামো স্থাপন করতে পারি। আমরা অনুমান করি যে, সুপ্ত কাঠামোর শর্তসাপেক্ষে, বিপুল সংখ্যক আউটপুট (চিত্রের পিক্সেল) একে অপরের থেকে স্বাধীন। এই মডেল প্রশিক্ষণ নিয়ে গঠিত
- মডেল প্যারামিটার অপ্টিমাইজ করা (কার্নেল ফাংশন প্যারামিটারের পাশাপাশি, যেমন, পর্যবেক্ষণ গোলমালের বৈচিত্র্য), এবং
- প্রতিটি প্রশিক্ষণ পর্যবেক্ষণের জন্য (চিত্র), সূচক সেটে একটি সংশ্লিষ্ট বিন্দু অবস্থান খোঁজা। সমস্ত অপ্টিমাইজেশান ডেটার প্রান্তিক লগ সম্ভাবনা সর্বাধিক করে করা যেতে পারে।
আমদানি
import numpy as np
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfk = tfp.math.psd_kernels
%pylab inline
Populating the interactive namespace from numpy and matplotlib
MNIST ডেটা লোড করুন
# Load the MNIST data set and isolate a subset of it.
(x_train, y_train), (_, _) = tf.keras.datasets.mnist.load_data()
N = 1000
small_x_train = x_train[:N, ...].astype(np.float64) / 256.
small_y_train = y_train[:N]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step 11501568/11490434 [==============================] - 0s 0us/step
প্রশিক্ষণযোগ্য ভেরিয়েবল প্রস্তুত করুন
আমরা যৌথভাবে 3টি মডেল প্যারামিটারের পাশাপাশি সুপ্ত ইনপুটগুলির প্রশিক্ষণ দেব৷
# Create some trainable model parameters. We will constrain them to be strictly
# positive when constructing the kernel and the GP.
unconstrained_amplitude = tf.Variable(np.float64(1.), name='amplitude')
unconstrained_length_scale = tf.Variable(np.float64(1.), name='length_scale')
unconstrained_observation_noise = tf.Variable(np.float64(1.), name='observation_noise')
# We need to flatten the images and, somewhat unintuitively, transpose from
# shape [100, 784] to [784, 100]. This is because the 784 pixels will be
# treated as *independent* conditioned on the latent inputs, meaning we really
# have a batch of 784 GP's with 100 index_points.
observations_ = small_x_train.reshape(N, -1).transpose()
# Create a collection of N 2-dimensional index points that will represent our
# latent embeddings of the data. (Lawrence, 2004) prescribes initializing these
# with PCA, but a random initialization actually gives not-too-bad results, so
# we use this for simplicity. For a fun exercise, try doing the
# PCA-initialization yourself!
init_ = np.random.normal(size=(N, 2))
latent_index_points = tf.Variable(init_, name='latent_index_points')
মডেল এবং প্রশিক্ষণ অপারেশন নির্মাণ
# Create our kernel and GP distribution
EPS = np.finfo(np.float64).eps
def create_kernel():
amplitude = tf.math.softplus(EPS + unconstrained_amplitude)
length_scale = tf.math.softplus(EPS + unconstrained_length_scale)
kernel = tfk.ExponentiatedQuadratic(amplitude, length_scale)
return kernel
def loss_fn():
observation_noise_variance = tf.math.softplus(
EPS + unconstrained_observation_noise)
gp = tfd.GaussianProcess(
kernel=create_kernel(),
index_points=latent_index_points,
observation_noise_variance=observation_noise_variance)
log_probs = gp.log_prob(observations_, name='log_prob')
return -tf.reduce_mean(log_probs)
trainable_variables = [unconstrained_amplitude,
unconstrained_length_scale,
unconstrained_observation_noise,
latent_index_points]
optimizer = tf.optimizers.Adam(learning_rate=1.0)
@tf.function(autograph=False, jit_compile=True)
def train_model():
with tf.GradientTape() as tape:
loss_value = loss_fn()
grads = tape.gradient(loss_value, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss_value
ফলে সুপ্ত এমবেডিংগুলিকে প্রশিক্ষণ দিন এবং প্লট করুন৷
# Initialize variables and train!
num_iters = 100
log_interval = 20
lips = np.zeros((num_iters, N, 2), np.float64)
for i in range(num_iters):
loss = train_model()
lips[i] = latent_index_points.numpy()
if i % log_interval == 0 or i + 1 == num_iters:
print("Loss at step %d: %f" % (i, loss))
Loss at step 0: 1108.121688 Loss at step 20: -159.633761 Loss at step 40: -263.014394 Loss at step 60: -283.713056 Loss at step 80: -288.709413 Loss at step 99: -289.662253
প্লট ফলাফল
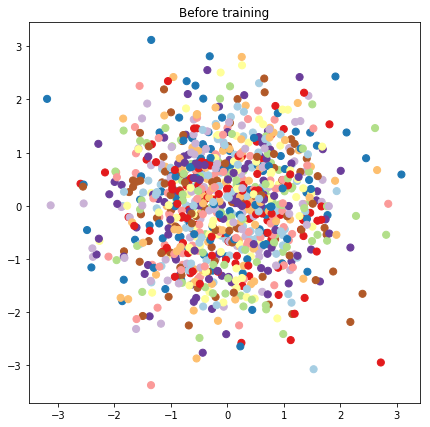
# Plot the latent locations before and after training
plt.figure(figsize=(7, 7))
plt.title("Before training")
plt.grid(False)
plt.scatter(x=init_[:, 0], y=init_[:, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
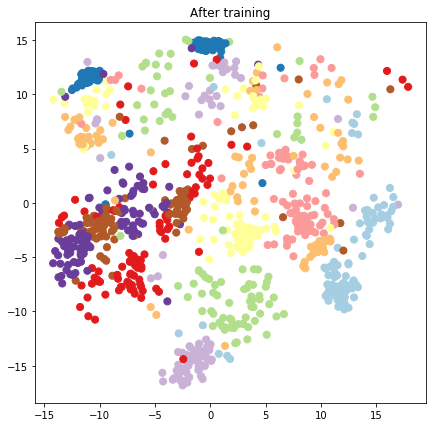
plt.figure(figsize=(7, 7))
plt.title("After training")
plt.grid(False)
plt.scatter(x=lips[-1, :, 0], y=lips[-1, :, 1],
c=y_train[:N], cmap=plt.get_cmap('Paired'), s=50)
plt.show()
ভবিষ্যদ্বাণীমূলক মডেল এবং স্যাম্পলিং অপারেশনগুলি তৈরি করুন
# We'll draw samples at evenly spaced points on a 10x10 grid in the latent
# input space.
sample_grid_points = 10
grid_ = np.linspace(-4, 4, sample_grid_points).astype(np.float64)
# Create a 10x10 grid of 2-vectors, for a total shape [10, 10, 2]
grid_ = np.stack(np.meshgrid(grid_, grid_), axis=-1)
# This part's a bit subtle! What we defined above was a batch of 784 (=28x28)
# independent GP distributions over the input space. Each one corresponds to a
# single pixel of an MNIST image. Now what we'd like to do is draw 100 (=10x10)
# *independent* samples, each one separately conditioned on all the observations
# as well as the learned latent input locations above.
#
# The GP regression model below will define a batch of 784 independent
# posteriors. We'd like to get 100 independent samples each at a different
# latent index point. We could loop over the points in the grid, but that might
# be a bit slow. Instead, we can vectorize the computation by tacking on *even
# more* batch dimensions to our GaussianProcessRegressionModel distribution.
# In the below grid_ shape, we have concatentaed
# 1. batch shape: [sample_grid_points, sample_grid_points, 1]
# 2. number of examples: [1]
# 3. number of latent input dimensions: [2]
# The `1` in the batch shape will broadcast with 784. The final result will be
# samples of shape [10, 10, 784, 1]. The `1` comes from the "number of examples"
# and we can just `np.squeeze` it off.
grid_ = grid_.reshape(sample_grid_points, sample_grid_points, 1, 1, 2)
# Create the GPRegressionModel instance which represents the posterior
# predictive at the grid of new points.
gprm = tfd.GaussianProcessRegressionModel(
kernel=create_kernel(),
# Shape [10, 10, 1, 1, 2]
index_points=grid_,
# Shape [1000, 2]. 1000 2 dimensional vectors.
observation_index_points=latent_index_points,
# Shape [784, 1000]. A batch of 784 1000-dimensional observations.
observations=observations_)
ডেটা এবং সুপ্ত এম্বেডিংয়ের শর্তযুক্ত নমুনা আঁকুন
আমরা সুপ্ত স্থানের একটি 2-ডি গ্রিডে 100 পয়েন্টে নমুনা করি।
samples = gprm.sample()
# Plot the grid of samples at new points. We do a bit of tweaking of the samples
# first, squeezing off extra 1-shapes and normalizing the values.
samples_ = np.squeeze(samples.numpy())
samples_ = ((samples_ -
samples_.min(-1, keepdims=True)) /
(samples_.max(-1, keepdims=True) -
samples_.min(-1, keepdims=True)))
samples_ = samples_.reshape(sample_grid_points, sample_grid_points, 28, 28)
samples_ = samples_.transpose([0, 2, 1, 3])
samples_ = samples_.reshape(28 * sample_grid_points, 28 * sample_grid_points)
plt.figure(figsize=(7, 7))
ax = plt.subplot()
ax.grid(False)
ax.imshow(-samples_, interpolation='none', cmap='Greys')
plt.show()

উপসংহার
আমরা গাউসিয়ান প্রক্রিয়ার সুপ্ত পরিবর্তনশীল মডেলের একটি সংক্ষিপ্ত সফর নিয়েছি এবং দেখিয়েছি কিভাবে আমরা TF এবং TF সম্ভাব্যতা কোডের কয়েকটি লাইনে এটি বাস্তবায়ন করতে পারি।
