 Xem trên TensorFlow.org Xem trên TensorFlow.org |  Chạy trong Google Colab Chạy trong Google Colab |  Xem nguồn trên GitHub Xem nguồn trên GitHub |  Tải xuống sổ ghi chép Tải xuống sổ ghi chép |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [copula] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) là một phương pháp cổ điển để chụp sự phụ thuộc giữa các biến ngẫu nhiên. Chính thức hơn, một copula là một phân phối đa biến \(C(U_1, U_2, ...., U_n)\) mà marginalizing cho \(U_i \sim \text{Uniform}(0, 1)\).
Copulas rất thú vị vì chúng ta có thể sử dụng chúng để tạo ra các phân phối đa biến với các biên tùy ý. Đây là công thức:
- Sử dụng Integral Xác suất chuyển đổi lần lượt một tùy RV liên tục \(X\) vào một bộ đồng phục một \(F_X(X)\), nơi \(F_X\) là CDF của \(X\).
- Cho một copula (nói hai biến) \(C(U, V)\), chúng tôi có mà \(U\) và \(V\) có phân bố biên thống nhất.
- Ngay bây giờ cho RV của chúng tôi là quan tâm \(X, Y\), tạo ra một phân phối mới \(C'(X, Y) = C(F_X(X), F_Y(Y))\). Các marginals cho \(X\) và \(Y\) là những người chúng ta mong muốn.
Biên là đơn biến và do đó có thể dễ dàng hơn để đo lường và / hoặc mô hình hóa. Một copula cho phép bắt đầu từ các biên nhưng cũng đạt được sự tương quan tùy ý giữa các kích thước.
Gaussian Copula
Để minh họa cách các công thức đồng biến được xây dựng, hãy xem xét trường hợp nắm bắt sự phụ thuộc theo các tương quan Gaussian đa biến. Một Gaussian copula là một trong do \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) nơi \(\Phi_\Sigma\) đại diện cho CDF của một MultivariateNormal, với hiệp phương sai \(\Sigma\) và trung bình 0 và \(\Phi^{-1}\) là CDF nghịch đảo cho các tiêu chuẩn bình thường.
Việc áp dụng CDF nghịch đảo của thông thường sẽ làm cong các kích thước đồng nhất được phân phối chuẩn. Việc áp dụng CDF của chuẩn tắc đa biến sau đó thu nhỏ phân phối để được đồng nhất một chút và với các tương quan Gauss.
Vì vậy, những gì chúng ta có được là Gaussian copula là một bản phân phối qua các đơn vị hypercube \([0, 1]^n\) với marginals thống nhất.
Định nghĩa như vậy, Gaussian copula có thể được thực hiện với tfd.TransformedDistribution và phù hợp Bijector . Nghĩa là, chúng ta đang chuyển đổi một MultivariateNormal, thông qua việc sử dụng các phân phối của Bình thường nghịch đảo CDF, thực hiện bởi tfb.NormalCDF bijector.
Dưới đây, chúng tôi thực hiện một Gaussian copula với một giả định đơn giản hóa: đó là các hiệp phương sai được tham số hóa bởi một yếu tố Cholesky (vì thế một hiệp phương sai cho MultivariateNormalTriL ). (Người ta có thể sử dụng khác tf.linalg.LinearOperators để mã hóa các giả định ma trận miễn phí khác.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
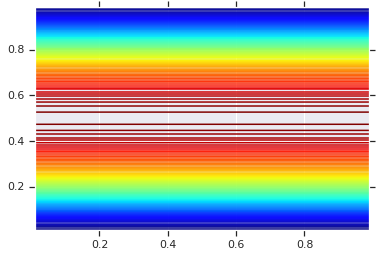
Tuy nhiên, sức mạnh từ một mô hình như vậy đang sử dụng Phép biến đổi Tích phân Xác suất, để sử dụng bản sao trên các RV tùy ý. Bằng cách này, chúng ta có thể chỉ định các biên tùy ý và sử dụng bản sao để ghép chúng lại với nhau.
Chúng tôi bắt đầu với một mô hình:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
và sử dụng copula để có được một hai biến RV \(Z\), trong đó có marginals Kumaraswamy và Gumbel .
Chúng tôi sẽ bắt đầu bằng cách vẽ biểu đồ phân phối sản phẩm được tạo ra bởi hai RV đó. Đây chỉ là để phục vụ như một điểm so sánh khi chúng tôi áp dụng Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
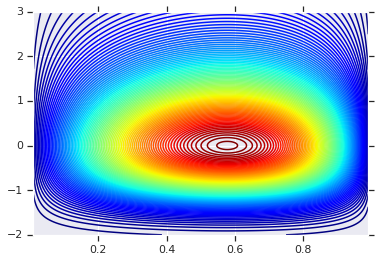
Phân phối chung với các biên khác nhau
Bây giờ chúng ta sử dụng một copula Gaussian để ghép các phân bố lại với nhau và vẽ biểu đồ đó. Một lần nữa công cụ của chúng tôi lựa chọn được TransformedDistribution áp dụng thích hợp Bijector để có được những marginals chọn.
Cụ thể, chúng tôi sử dụng một Blockwise bijector áp dụng bijectors khác nhau ở các phần khác nhau của vector (mà vẫn còn là một chuyển đổi song ánh).
Bây giờ chúng ta có thể xác định Copula mà chúng ta muốn. Đưa ra danh sách các biên mục tiêu (được mã hóa dưới dạng bijector), chúng ta có thể dễ dàng tạo một phân phối mới sử dụng copula và có các biên được chỉ định.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Cuối cùng, hãy thực sự sử dụng Gaussian Copula này. Chúng tôi sẽ sử dụng một Cholesky của \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), mà sẽ tương ứng với phương sai 1, và tương quan \(\rho\) cho việc bình thường đa biến.
Chúng ta sẽ xem xét một số trường hợp:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
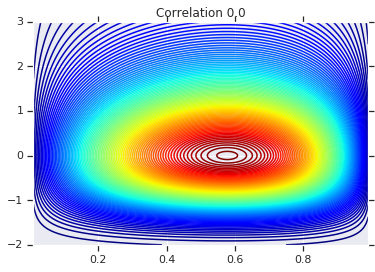
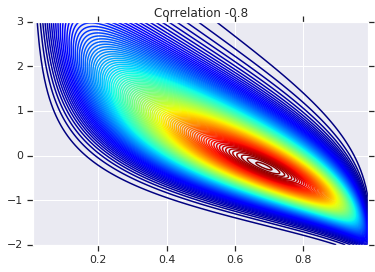
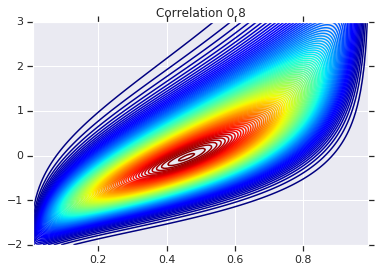
Cuối cùng, hãy xác minh rằng chúng tôi thực sự nhận được những lợi nhuận mà chúng tôi muốn.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
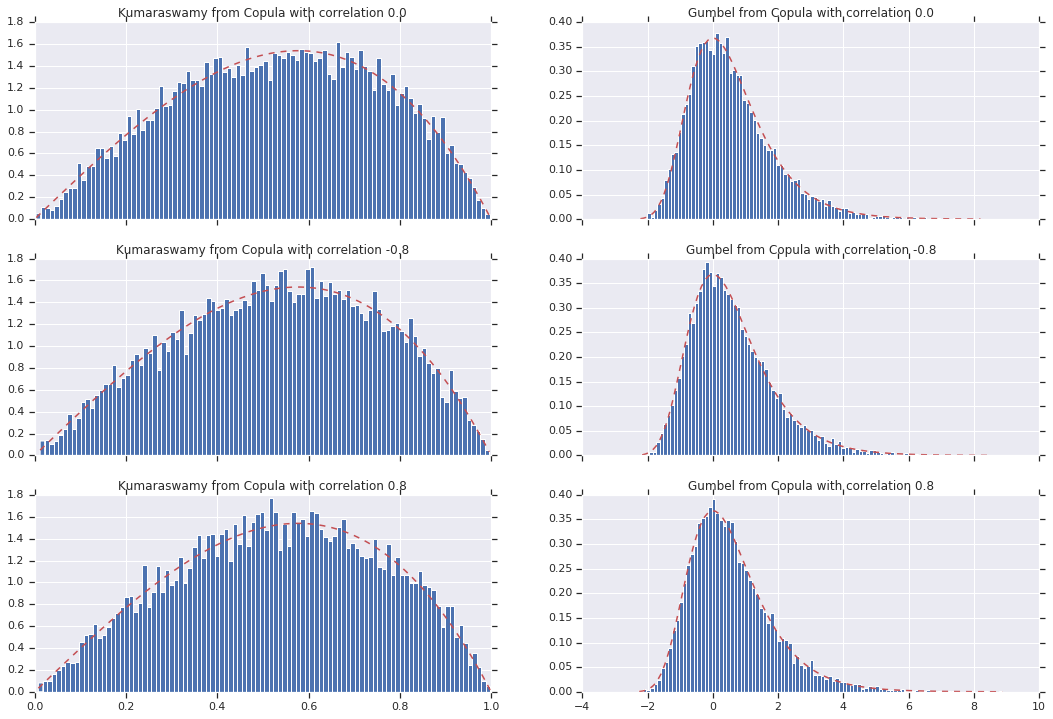
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Sự kết luận
Và chúng ta bắt đầu! Chúng tôi đã chứng minh rằng chúng ta có thể xây dựng Gaussian Copulas sử dụng Bijector API.
Tổng quát hơn, viết bijectors sử dụng Bijector API và sáng tác chúng với một phân phối, có thể tạo ra những gia đình giàu có của các bản phân phối cho mô hình linh hoạt.
