 Посмотреть на TensorFlow.org Посмотреть на TensorFlow.org |  Запускаем в Google Colab Запускаем в Google Colab |  Посмотреть исходный код на GitHub Посмотреть исходный код на GitHub |  Скачать блокнот Скачать блокнот |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
А [копула] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) представляет собой классический подход для захвата зависимости между случайными величинами. Более формально, связка представляет собой многомерное распределение \(C(U_1, U_2, ...., U_n)\) таким образом, что маргинализации дает \(U_i \sim \text{Uniform}(0, 1)\).
Копулы интересны тем, что мы можем использовать их для создания многомерных распределений с произвольными маргиналами. Это рецепт:
- Использование вероятностей интегрального преобразования превращает произвольную непрерывную RV \(X\) в одном равномерное \(F_X(X)\), где \(F_X\) является ВПР из \(X\).
- Учитывая копула (скажем двумерным) \(C(U, V)\), мы имеем , что \(U\) и \(V\) имеют единые предельные распределения.
- Теперь с учетом нашего RV , представляющие интерес для \(X, Y\), создать новое распределение \(C'(X, Y) = C(F_X(X), F_Y(Y))\). Маргинальные для \(X\) и \(Y\) являются те , которые мы желательными.
Маржа являются одномерными, поэтому их легче измерить и / или смоделировать. Связка позволяет начать с маргиналов, но при этом добиться произвольной корреляции между размерами.
Гауссовская копула
Чтобы проиллюстрировать, как строятся связки, рассмотрим случай захвата зависимости в соответствии с многомерными гауссовыми корреляциями. Гауссово Связка один задается \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) , где \(\Phi_\Sigma\) представляет собой CDF из в MultivariateNormal, с ковариационной \(\Sigma\) и средним 0 и \(\Phi^{-1}\) является обратным ВПР для стандартного нормального.
Применение обратного CDF нормали искажает однородные размеры, чтобы они были распределены нормально. Применяя CDF многомерной нормали, затем сужает распределение до минимально однородного и с гауссовыми корреляциями.
Таким образом, то , что мы получаем , что гауссова Связкой является распределением по единичному гиперкубу \([0, 1]^n\) с равномерными маргинальными.
Определяется как , например, гауссова Связка может быть реализована с tfd.TransformedDistribution и соответствующим Bijector . То есть, мы превращаем MultivariateNormal, посредством использования нормального распределения обратного ВПР - х, реализуемой tfb.NormalCDF bijector.
Ниже мы реализуем Gaussian Копулу с упрощающим предположением , что ковариационная параметризирован фактором Холецкого (отсюда ковариациями для MultivariateNormalTriL ). (Можно было бы использовать другие tf.linalg.LinearOperators кодировать различные предположения нематричный.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
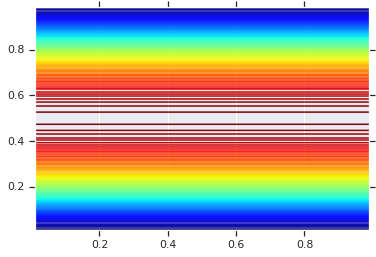
Однако сила такой модели заключается в использовании интегрального преобразования вероятности для использования связки на произвольных RV. Таким образом, мы можем указать произвольные маргиналы и использовать связку, чтобы сшить их вместе.
Начнем с модели:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
и использовать связку , чтобы получить двухмерную RV \(Z\), который имеет маргинал Кумарасва и Гамбель .
Мы начнем с построения графика распределения продуктов, созданного этими двумя RV. Это просто для сравнения с тем, когда мы применяем Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
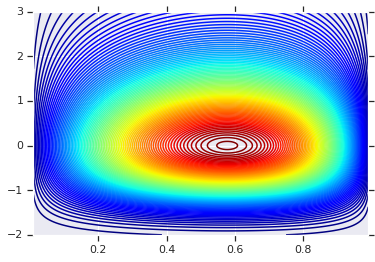
Совместное распределение с разной маржой
Теперь мы используем гауссову связку, чтобы связать распределения вместе, и построить график. Опять наш инструмент выбора является TransformedDistribution применения соответствующего Bijector получить выбранные маргинал.
В частности, мы используем Blockwise bijector , который применяет различный bijectors на разные части вектора (который до сих пор биективное преобразование).
Теперь мы можем определить желаемую Copula. Имея список целевых маргиналов (закодированных как bijectors), мы можем легко построить новое распределение, которое использует копулу и имеет указанные маргиналы.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Наконец, давайте на самом деле воспользуемся этой гауссовой копулой. Мы будем использовать Холецкий \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), который будет соответствовать дисперсиям 1 и корреляция \(\rho\) для многомерных нормального.
Мы рассмотрим несколько случаев:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
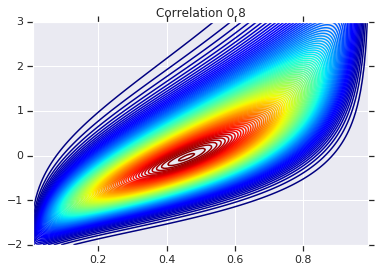
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
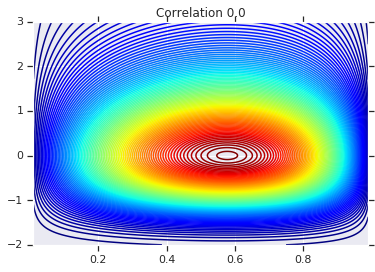
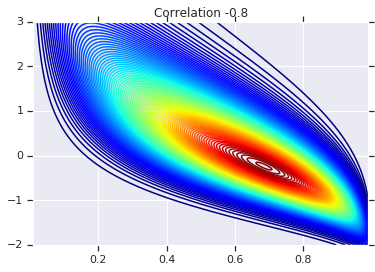
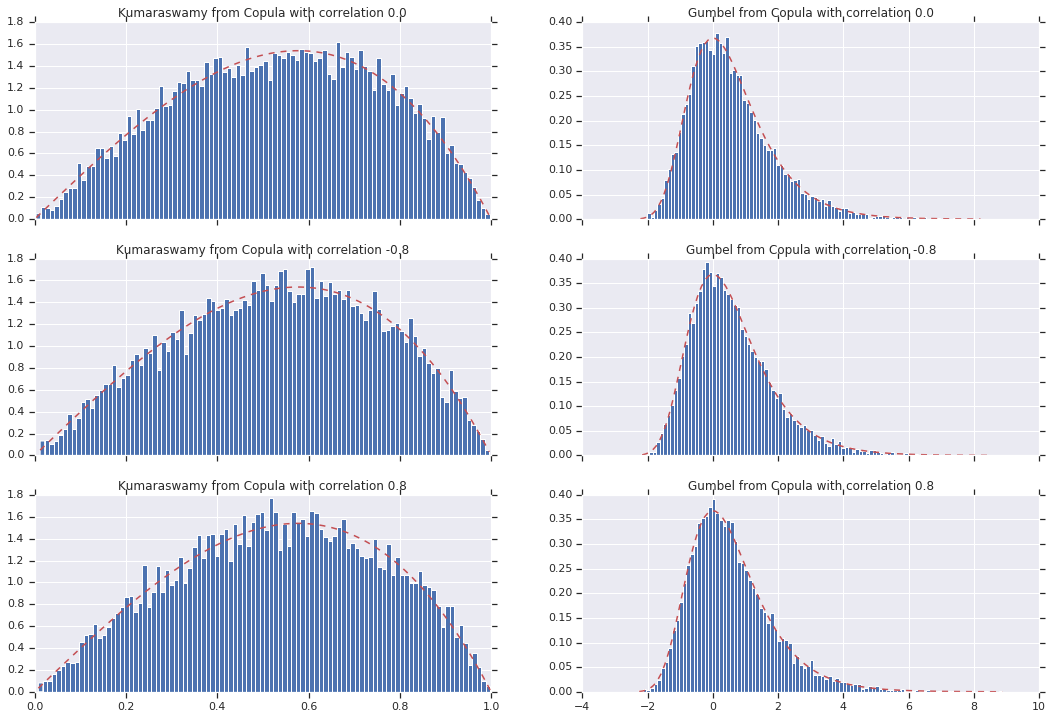
Наконец, давайте проверим, действительно ли мы получили нужные маргиналы.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Вывод
И вот так! Мы показали , что мы можем построить Gaussian связки с помощью Bijector API.
В целом, написание bijectors с использованием Bijector API и наборные их с распределением, может создавать богатые семейства распределений для гибкого моделирования.
