 Zobacz na TensorFlow.org Zobacz na TensorFlow.org |  Uruchom w Google Colab Uruchom w Google Colab |  Wyświetl źródło na GitHub Wyświetl źródło na GitHub |  Pobierz notatnik Pobierz notatnik |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [kopuła] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) jest klasycznym podejściem do uchwycenia zależności między zmiennymi losowymi. Więcej Formalnie kopuła jest wieloczynnikowa rozkład \(C(U_1, U_2, ...., U_n)\) tak, że marginalizację daje \(U_i \sim \text{Uniform}(0, 1)\).
Kopuły są interesujące, ponieważ możemy je wykorzystać do tworzenia rozkładów wielowymiarowych z arbitralnymi marginesami. Oto przepis:
- Za pomocą integralnych prawdopodobieństwa Transform zamienia dowolnego ciągłego RV \(X\) w jednorodną jednej \(F_X(X)\), gdzie \(F_X\) jest CDF \(X\).
- Biorąc pod uwagę spójka (słownie dwuwymiarowym) \(C(U, V)\), że mamy \(U\) i \(V\) mieć jednolite marginalne rozkładów.
- Teraz biorąc pod uwagę nasze RV turystyczne \(X, Y\)utwórz nowy dystrybucji \(C'(X, Y) = C(F_X(X), F_Y(Y))\). W marginals dla \(X\) i \(Y\) są te, które pożądane.
Marginesy są jednowymiarowe i dlatego mogą być łatwiejsze do zmierzenia i/lub modelowania. Kopuła umożliwia rozpoczęcie od marginesów, ale także osiągnięcie dowolnej korelacji między wymiarami.
Kopuła Gaussa
Aby zilustrować, jak zbudowane są kopuły, rozważmy przypadek uchwycenia zależności zgodnie z wielowymiarowymi korelacjami Gaussa. Gaussowski Copula jest podane przez \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) gdzie \(\Phi_\Sigma\) reprezentuje CDF na MultivariateNormal z kowariancji \(\Sigma\) i średnią wartość 0, a \(\Phi^{-1}\) jest CDF odwrotny dla rozkładu normalnego.
Zastosowanie odwrotnego CDF normalnej powoduje wypaczenie jednolitych wymiarów, które mają być rozłożone normalnie. Zastosowanie współczynnika CDF wielowymiarowej normalnej powoduje zgniecenie rozkładu tak, aby był marginalnie jednorodny i miał korelacje Gaussa.
Tak więc, co mamy jest to, że Gaussa Copula jest dystrybucja przez jednostkę hipersześcianu \([0, 1]^n\) z jednolitymi uzupełnieniach.
Definiowany jako taki, Gaussian Copula mogą być realizowane z tfd.TransformedDistribution i odpowiedniego Bijector . Oznacza to, że jesteśmy przekształcania MultivariateNormal, poprzez wykorzystanie rozkładu normalnego na odwrotność CDF, realizowanego przez tfb.NormalCDF bijector.
Poniżej wdrożyć Gaussa kopuła z jednym upraszcza założeniu: że kowariancja jest parametryzowane przez współczynnik Choleskiego (stąd kowariancji dla MultivariateNormalTriL ). (Można stosować inne tf.linalg.LinearOperators kodować różne założenia matrycy wolnej.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
Jednak siła takiego modelu polega na wykorzystaniu transformacji całkowej prawdopodobieństwa, aby użyć kopuły na dowolnych RV. W ten sposób możemy określić dowolne marginesy i użyć kopuły do ich połączenia.
Zaczynamy od modelu:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
i korzystać z kopułę dostać dwuwymiarowym RV \(Z\), który ma marginesowymi Kumaraswamy i Gumbela .
Zaczniemy od wykreślenia rozkładu produktu generowanego przez te dwa RV. Służy to jedynie jako punkt porównawczy do zastosowania kopuły.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
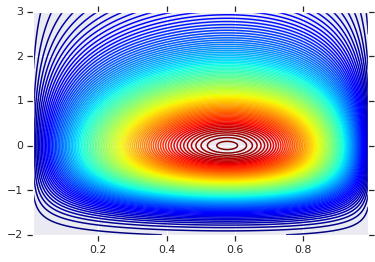
Wspólna dystrybucja z różnymi marginesami
Teraz używamy kopuły Gaussa do sprzężenia rozkładów i wykreślenia tego. Znowu nasze narzędzie wyboru jest TransformedDistribution zastosowanie odpowiedniego Bijector uzyskanie wybranych marginesowymi.
Konkretnie, używamy Blockwise bijector który stosuje różne bijectors w różnych częściach wektora (która jest nadal bijective transformacja).
Teraz możemy zdefiniować pożądaną kopułę. Mając listę docelowych marginesów (zakodowanych jako bijectors), możemy łatwo skonstruować nowy rozkład, który używa kopuły i ma określone marginesy.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Na koniec użyjmy tej kopuły Gaussa. Użyjemy Cholesky z \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), która będzie odpowiadać wariancji 1 i korelacji \(\rho\) dla wieloczynnikowej normalne.
Przyjrzymy się kilku przypadkom:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
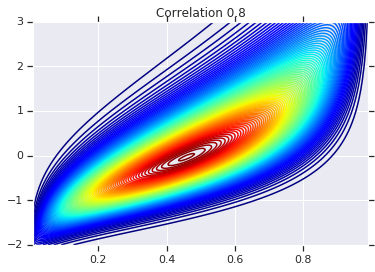
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
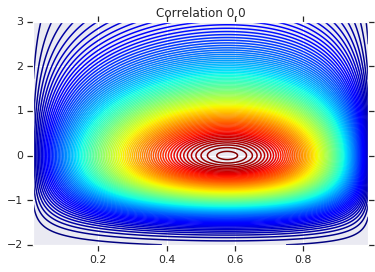
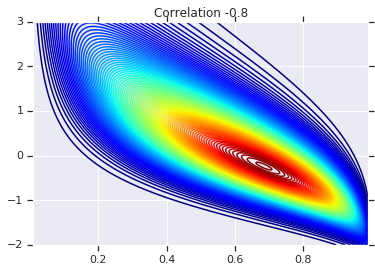
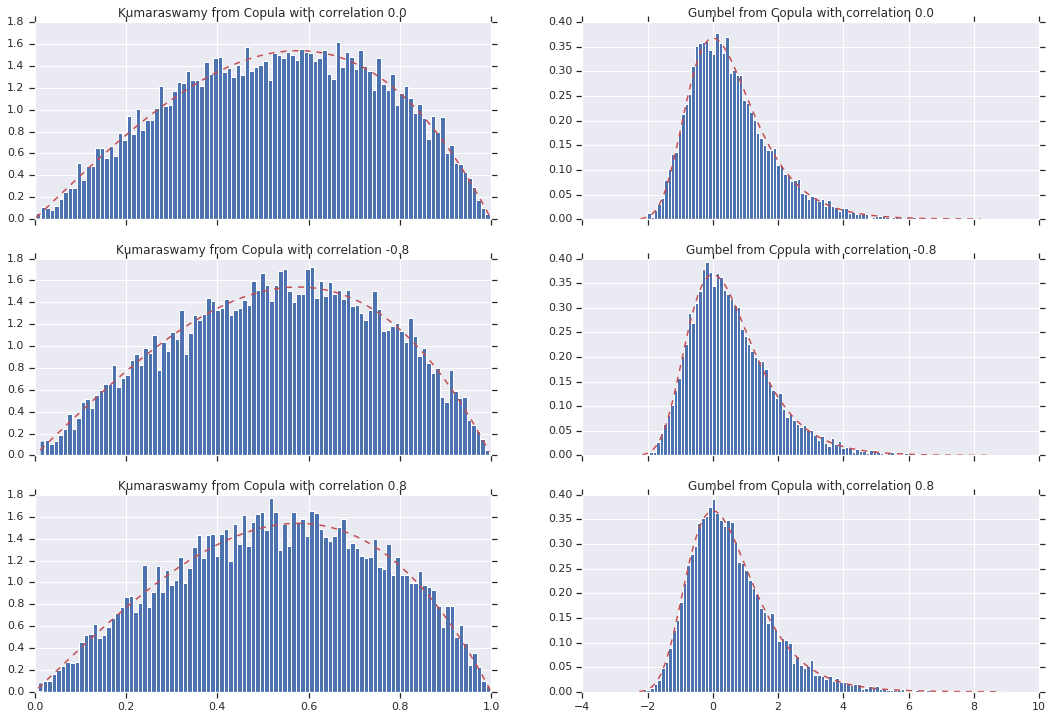
Na koniec zweryfikujmy, czy rzeczywiście otrzymujemy marginesy, jakich chcemy.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Wniosek
I gotowe! Musimy wykazać, że możemy skonstruować Gaussa copulas pomocą Bijector API.
Mówiąc bardziej ogólnie, pisząc bijectors pomocą Bijector API i kompozytorskie ich dystrybucji, mogą tworzyć bogate rodziny rozkładów dla elastycznego modelowania.
