 Visualizza su TensorFlow.org Visualizza su TensorFlow.org |  Esegui in Google Colab Esegui in Google Colab |  Visualizza la fonte su GitHub Visualizza la fonte su GitHub |  Scarica taccuino Scarica taccuino |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [copula] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) è un approccio classico per catturare la dipendenza tra variabili casuali. Più formalmente, una copula è una distribuzione multivariata \(C(U_1, U_2, ...., U_n)\) tale che marginalizzante dà \(U_i \sim \text{Uniform}(0, 1)\).
Le copule sono interessanti perché possiamo usarle per creare distribuzioni multivariate con marginali arbitrari. Questa è la ricetta:
- Usando l' integrale Probabilità Transform spire un'arbitraria continuo RV \(X\) in un'uniforme uno \(F_X(X)\), dove \(F_X\) è CDF di \(X\).
- Data una copula (diciamo bivariata) \(C(U, V)\), abbiamo che \(U\) e \(V\) hanno distribuzioni marginali uniformi.
- Ora dato il nostro camper è di interesse \(X, Y\), creare una distribuzione nuova \(C'(X, Y) = C(F_X(X), F_Y(Y))\). I marginali per \(X\) e \(Y\) sono quelli che desiderate.
I marginali sono univariati e quindi possono essere più facili da misurare e/o modellare. Una copula consente di partire dai marginali ma anche di ottenere una correlazione arbitraria tra le dimensioni.
Copula gaussiana
Per illustrare come vengono costruite le copule, si consideri il caso della cattura della dipendenza secondo correlazioni gaussiane multivariate. Un gaussiana Copula è uno in \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) dove \(\Phi_\Sigma\) rappresenta la CDF di un MultivariateNormal, con covarianza \(\Sigma\) e media 0 e \(\Phi^{-1}\) è la CDF inversa per lo standard normale.
L'applicazione del CDF inverso della normale deforma le dimensioni uniformi per essere distribuite normalmente. L'applicazione della CDF della normale multivariata riduce quindi la distribuzione in modo che sia marginalmente uniforme e con correlazioni gaussiane.
Così, ciò che otteniamo è che la gaussiana Copula è una distribuzione sopra l'unità ipercubo \([0, 1]^n\) con marginali uniformi.
Definito come tale, il gaussiana Copula può essere implementato con tfd.TransformedDistribution e appropriato Bijector . Cioè, stiamo trasformando un MultivariateNormal, attraverso l'utilizzo della distribuzione normale del inversa CDF, attuato dal tfb.NormalCDF bijector.
Qui di seguito, abbiamo attuare una gaussiana con una Copula assunzione semplificativa: che la covarianza è parametrizzato da un fattore di Cholesky (quindi una covarianza per MultivariateNormalTriL ). (Si potrebbe utilizzare altri tf.linalg.LinearOperators per codificare differenti ipotesi privo di matrice.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
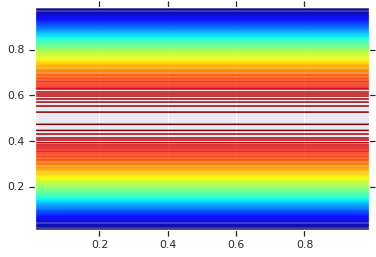
Il potere, tuttavia, di un tale modello sta nell'usare la Trasformata Integrale di Probabilità, per usare la copula su RV arbitrari. In questo modo, possiamo specificare marginali arbitrari e usare la copula per unirli insieme.
Partiamo da un modello:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
e utilizzare la copula per ottenere un bivariata RV \(Z\), che ha marginali Kumaraswamy e Gumbel .
Inizieremo tracciando la distribuzione del prodotto generata da quei due RV Questo serve solo come punto di confronto per quando applichiamo la Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
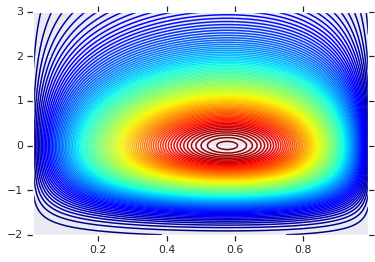
Distribuzione congiunta con marginali diversi
Ora usiamo una copula gaussiana per accoppiare le distribuzioni e tracciarlo. Anche in questo caso il nostro strumento di scelta è TransformedDistribution applicando l'appropriata Bijector per ottenere i marginali scelti.
Specificamente, si usa un Blockwise bijector che applica differenti bijectors in diverse parti del vettore (che è ancora una trasformazione biunivoca).
Ora possiamo definire la Copula che vogliamo. Data una lista di marginali target (codificati come bijectors), possiamo facilmente costruire una nuova distribuzione che usi la copula e abbia i marginali specificati.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Infine, usiamo effettivamente questa copula gaussiana. Useremo una Cholesky di \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), che corrisponderà alla varianze 1, e correlazione \(\rho\) per la normale multivariata.
Esamineremo alcuni casi:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
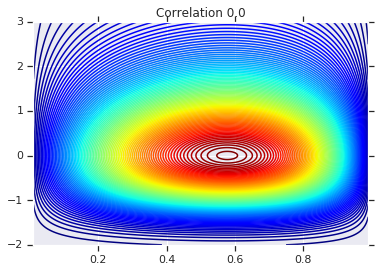
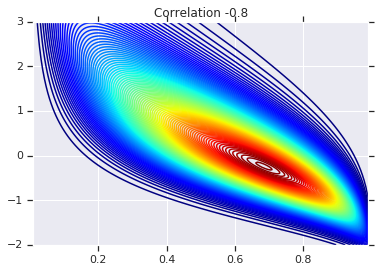
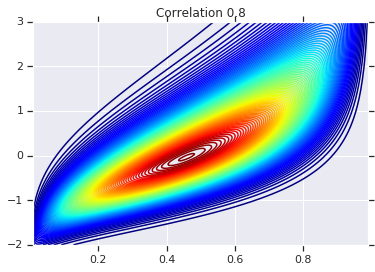
Infine, verifichiamo che otteniamo effettivamente i marginali desiderati.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
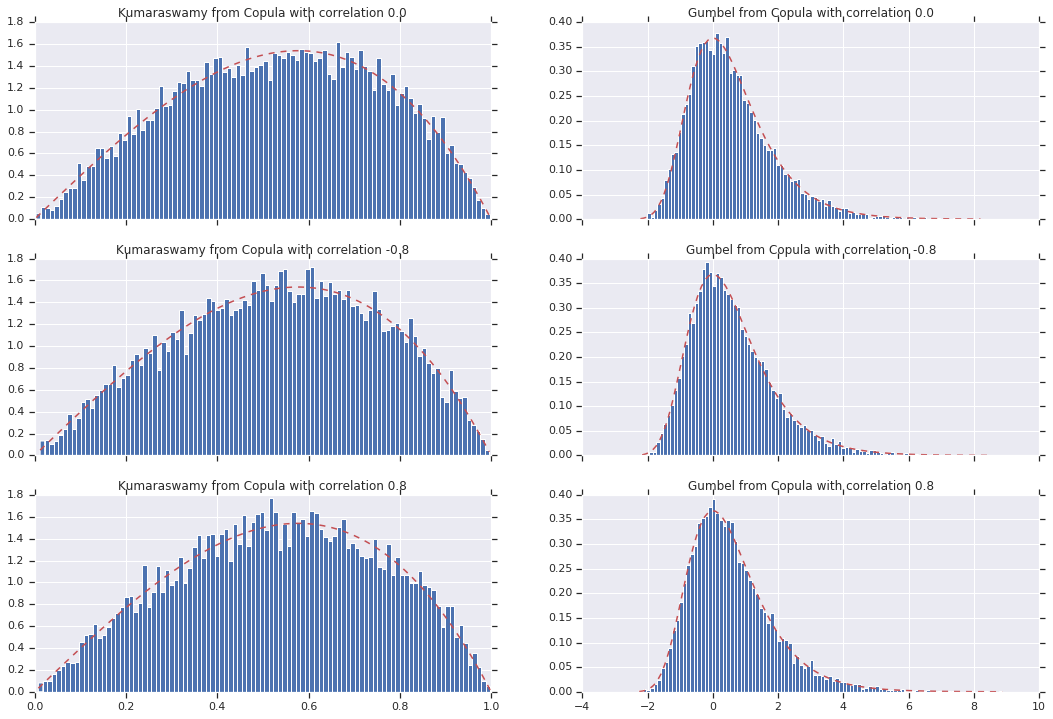
Conclusione
E ci siamo! Abbiamo dimostrato che possiamo costruire gaussiana Copule utilizzando il Bijector API.
Più in generale, la scrittura bijectors utilizzando l' Bijector API e li compongono con una distribuzione, può creare ricche famiglie di distribuzioni per modellazione flessibile.
