 Lihat di TensorFlow.org Lihat di TensorFlow.org |  Jalankan di Google Colab Jalankan di Google Colab |  Lihat sumber di GitHub Lihat sumber di GitHub |  Unduh buku catatan Unduh buku catatan |
import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
A [kopula] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) adalah pendekatan klasik untuk menangkap ketergantungan antara variabel acak. Lebih formal, kata kerja penghubung adalah distribusi multivariat \(C(U_1, U_2, ...., U_n)\) sehingga meminggirkan memberikan \(U_i \sim \text{Uniform}(0, 1)\).
Kopula menarik karena kita dapat menggunakannya untuk membuat distribusi multivariat dengan marjinal yang berubah-ubah. Ini resepnya:
- Menggunakan Integral Probability Transform bergantian sewenang-wenang terus menerus RV \(X\) menjadi seragam satu \(F_X(X)\), di mana \(F_X\) adalah CDF dari \(X\).
- Mengingat kerja penghubung (katakanlah bivariat) \(C(U, V)\), kita mendapati bahwa \(U\) dan \(V\) memiliki distribusi marjinal seragam.
- Sekarang diberikan RV kami adalah bunga \(X, Y\), membuat distribusi baru \(C'(X, Y) = C(F_X(X), F_Y(Y))\). The marginals untuk \(X\) dan \(Y\) adalah orang-orang yang kita inginkan.
Marginal bersifat univariat dan dengan demikian mungkin lebih mudah untuk diukur dan/atau dimodelkan. Sebuah kopula memungkinkan mulai dari marjinal namun juga mencapai korelasi sewenang-wenang antar dimensi.
Kopula Gauss
Untuk mengilustrasikan bagaimana kopula dibangun, pertimbangkan kasus menangkap ketergantungan menurut korelasi Gaussian multivariat. Sebuah Gaussian Penghubung adalah salah satu yang diberikan oleh \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) mana \(\Phi_\Sigma\) merupakan CDF dari MultivariateNormal, dengan kovarians \(\Sigma\) dan mean 0, dan \(\Phi^{-1}\) adalah CDF terbalik untuk standar normal.
Menerapkan CDF terbalik normal membelokkan dimensi seragam menjadi terdistribusi normal. Menerapkan CDF normal multivariat kemudian menekan distribusi menjadi sedikit seragam dan dengan korelasi Gaussian.
Jadi, apa yang kita dapatkan adalah bahwa Gaussian Penghubung adalah distribusi melalui unit hypercube \([0, 1]^n\) dengan marginals seragam.
Didefinisikan seperti itu, Gaussian Penghubung dapat diimplementasikan dengan tfd.TransformedDistribution dan tepat Bijector . Artinya, kita mengubah sebuah MultivariateNormal, melalui penggunaan distribusi Normal terbalik CDF, dilaksanakan oleh tfb.NormalCDF bijector.
Di bawah ini, kami menerapkan Gaussian Penghubung dengan satu asumsi penyederhanaan: bahwa kovarians yang parameterized dengan faktor Cholesky (karenanya kovarians untuk MultivariateNormalTriL ). (Satu bisa menggunakan lainnya tf.linalg.LinearOperators untuk mengkodekan asumsi matriks bebas yang berbeda.).
class GaussianCopulaTriL(tfd.TransformedDistribution):
"""Takes a location, and lower triangular matrix for the Cholesky factor."""
def __init__(self, loc, scale_tril):
super(GaussianCopulaTriL, self).__init__(
distribution=tfd.MultivariateNormalTriL(
loc=loc,
scale_tril=scale_tril),
bijector=tfb.NormalCDF(),
validate_args=False,
name="GaussianCopulaTriLUniform")
# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
[x_grid[..., np.newaxis],
y_grid[..., np.newaxis]], axis=-1)
pdf = GaussianCopulaTriL(
loc=[0., 0.],
scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)
# Plot its density.
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
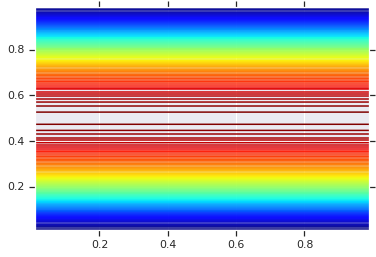
Namun, kekuatan dari model seperti itu adalah menggunakan Transformasi Integral Probabilitas, untuk menggunakan kopula pada RV arbitrer. Dengan cara ini, kita dapat menentukan marginal arbitrer, dan menggunakan kopula untuk menyatukannya.
Kita mulai dengan sebuah model:
\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]
dan menggunakan kata kerja penghubung untuk mendapatkan bivariat RV \(Z\), yang memiliki marginals Kumaraswamy dan Gumbel .
Kita akan mulai dengan memplot distribusi produk yang dihasilkan oleh kedua RV tersebut. Ini hanya untuk dijadikan sebagai titik perbandingan ketika kita menerapkan Copula.
a = 2.0
b = 2.0
gloc = 0.
gscale = 1.
x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)
# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)
pdf = x.prob(x_grid) * y.prob(y_grid)
# Plot its density
plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);
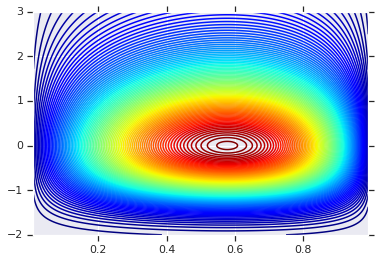
Distribusi Bersama dengan Marjinal Berbeda
Sekarang kita menggunakan kopula Gaussian untuk menggabungkan distribusi bersama-sama, dan memplotnya. Sekali lagi alat kami pilihan yang TransformedDistribution menerapkan sesuai Bijector untuk mendapatkan marginal yang dipilih.
Secara khusus, kami menggunakan Blockwise bijector yang berlaku bijectors berbeda pada bagian yang berbeda dari vektor (yang masih transformasi bijective).
Sekarang kita dapat mendefinisikan Copula yang kita inginkan. Diberikan daftar marjinal target (dikodekan sebagai bijektor), kita dapat dengan mudah membangun distribusi baru yang menggunakan kopula dan memiliki marjinal yang ditentukan.
class WarpedGaussianCopula(tfd.TransformedDistribution):
"""Application of a Gaussian Copula on a list of target marginals.
This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
which are distributed marginally (with CDF) [F_0, ... F_n],
`GaussianCopula` represents an application of the Copula, such that the
resulting multivariate distribution has the above specified marginals.
The marginals are specified by `marginal_bijectors`: These are
bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.
block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
length should be same as length of `marginal_bijectors`.
See tfb.Blockwise for details
"""
def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
super(WarpedGaussianCopula, self).__init__(
distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
bijector=tfb.Blockwise(bijectors=marginal_bijectors,
block_sizes=block_sizes),
validate_args=False,
name="GaussianCopula")
Akhirnya, mari kita gunakan Gaussian Copula ini. Kami akan menggunakan Cholesky dari \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), yang akan sesuai dengan varians 1, dan korelasi \(\rho\) untuk normal multivariat.
Kita akan melihat beberapa kasus:
# Create our coordinates:
coordinates = np.concatenate(
[x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)
def create_gaussian_copula(correlation):
# Use Gaussian Copula to add dependence.
return WarpedGaussianCopula(
loc=[0., 0.],
scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
# These encode the marginals we want. In this case we want X_0 has
# Kumaraswamy marginal, and X_1 has Gumbel marginal.
marginal_bijectors=[
tfb.Invert(tfb.KumaraswamyCDF(a, b)),
tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])
# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
copula = create_gaussian_copula(correlation)
copulas.append(copula)
probs.append(copula.prob(coordinates))
# Plot it's density
for correlation, copula_prob in zip(correlations, probs):
plt.figure()
plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
plt.title('Correlation {}'.format(correlation))
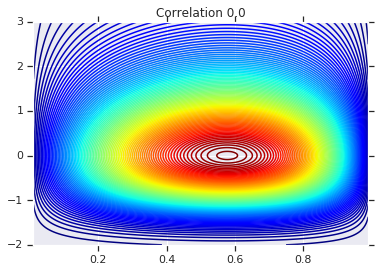
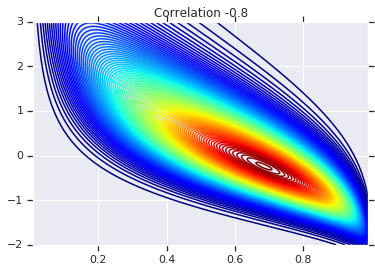
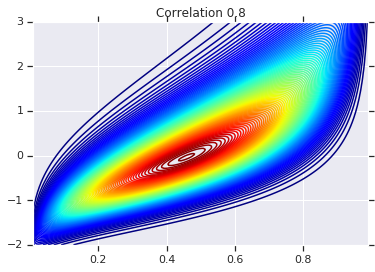
Akhirnya, mari kita verifikasi bahwa kita benar-benar mendapatkan marginal yang kita inginkan.
def kumaraswamy_pdf(x):
return tfd.Kumaraswamy(a, b).prob(np.float32(x))
def gumbel_pdf(x):
return tfd.Gumbel(gloc, gscale).prob(np.float32(x))
copula_samples = []
for copula in copulas:
copula_samples.append(copula.sample(10000))
plot_rows = len(correlations)
plot_cols = 2 # for 2 densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))
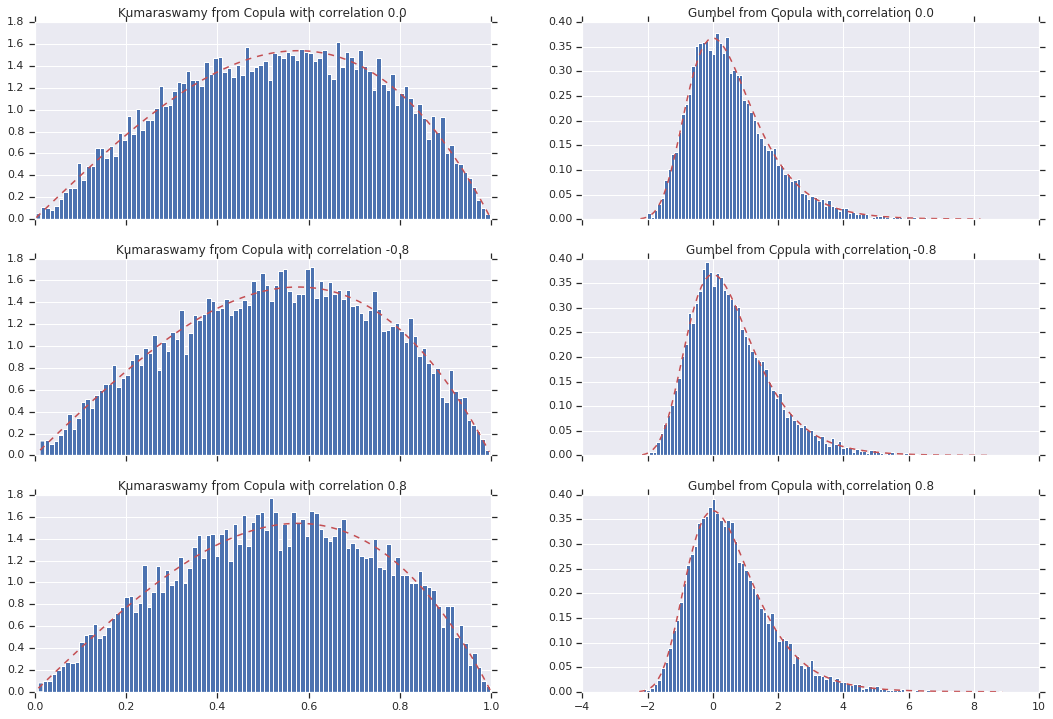
# Let's marginalize out on each, and plot the samples.
for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
k = copula_sample[..., 0].numpy()
g = copula_sample[..., 1].numpy()
_, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))
_, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))
Kesimpulan
Dan di sana kita pergi! Kami telah menunjukkan bahwa kami bisa membangun Gaussian Copulas menggunakan Bijector API.
Lebih umum, menulis bijectors menggunakan Bijector API dan menyusun mereka dengan distribusi, dapat membuat keluarga kaya distribusi untuk pemodelan fleksibel.
