TensorFlow.org पर देखें

Google Colab में चलाएं

GitHub पर स्रोत देखें

नोटबुक डाउनलोड करें

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

एक [योजक] (https://en.wikipedia.org/wiki/Copula_ (probability_theory% 29) यादृच्छिक चर के बीच निर्भरता पर कब्जा करने के लिए एक शास्त्रीय दृष्टिकोण है। अधिक औपचारिक रूप से, एक योजक बहुविविध वितरण है \(C(U_1, U_2, ...., U_n)\) ऐसी है कि दरकिनार देता है \(U_i \sim \text{Uniform}(0, 1)\)।

कोपुला दिलचस्प हैं क्योंकि हम उनका उपयोग मनमाने ढंग से सीमांत के साथ बहुभिन्नरूपी वितरण बनाने के लिए कर सकते हैं। यह नुस्खा है:

• का उपयोग करते हुए संभावना इंटीग्रल रूपांतरण बदल जाता है एक मनमाना निरंतर आर.वी. \(X\) एक समान एक में \(F_X(X)\), जहां \(F_X\) की CDF है \(X\)।
• एक योजक (माना द्विचर) को देखते हुए \(C(U, V)\), हम उस राशि \(U\) और \(V\) वर्दी सीमांत वितरण की है।
• अब हमारी आर.वी. ब्याज की है दी \(X, Y\), एक नया वितरण बनाने \(C'(X, Y) = C(F_X(X), F_Y(Y))\)। के लिए marginals \(X\) और \(Y\) जिन्हें हम वांछित हैं।

सीमांत अविभाज्य हैं और इस प्रकार मापना और/या मॉडल करना आसान हो सकता है। एक कोपुला सीमांत से शुरू करने में सक्षम बनाता है फिर भी आयामों के बीच मनमाना सहसंबंध प्राप्त करता है।

गाऊसी कोपुला

यह स्पष्ट करने के लिए कि युग्मज का निर्माण कैसे किया जाता है, बहुभिन्नरूपी गाऊसी सहसंबंधों के अनुसार निर्भरता पर कब्जा करने के मामले पर विचार करें। एक गाऊसी योजक एक द्वारा दिए गए है \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) जहां \(\Phi_\Sigma\) , एक MultivariateNormal की CDF का प्रतिनिधित्व करता है सहप्रसरण साथ \(\Sigma\) और मतलब 0, और \(\Phi^{-1}\) मानक सामान्य के लिए उलटा CDF है।

सामान्य के व्युत्क्रम सीडीएफ को लागू करने से समान आयामों को सामान्य रूप से वितरित किया जाता है। बहुभिन्नरूपी सामान्य के सीडीएफ को लागू करने के बाद वितरण को मामूली रूप से समान और गाऊसी सहसंबंधों के साथ स्क्वैश किया जाता है।

इस प्रकार, हम क्या मिलता है कि गाऊसी योजक इकाई hypercube पर एक वितरण है \([0, 1]^n\) वर्दी marginals साथ।

इस तरह के रूप में परिभाषित किया, गाऊसी योजक के साथ लागू किया जा सकता tfd.TransformedDistribution और उचित Bijector । यही कारण है, हम एक MultivariateNormal बदलने रहे हैं सामान्य वितरण के CDF उलटा का उपयोग करते हैं, द्वारा कार्यान्वित के माध्यम से, tfb.NormalCDF bijector।

नीचे, हम एक सरल बनाने धारणा के साथ एक गाऊसी योजक लागू: कि सहप्रसरण एक Cholesky कारक (इसलिए के लिए एक सहप्रसरण द्वारा parameterized है MultivariateNormalTriL )। (एक अन्य इस्तेमाल कर सकते हैं tf.linalg.LinearOperators अलग मैट्रिक्स मुक्त मान्यताओं एन्कोड करने के लिए।)।

class GaussianCopulaTriL(tfd.TransformedDistribution):
  """Takes a location, and lower triangular matrix for the Cholesky factor."""
  def __init__(self, loc, scale_tril):
    super(GaussianCopulaTriL, self).__init__(
        distribution=tfd.MultivariateNormalTriL(
            loc=loc,
            scale_tril=scale_tril),
        bijector=tfb.NormalCDF(),
        validate_args=False,
        name="GaussianCopulaTriLUniform")


# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
    [x_grid[..., np.newaxis],
     y_grid[..., np.newaxis]], axis=-1)

pdf = GaussianCopulaTriL(
    loc=[0., 0.],
    scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)

# Plot its density.

plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);

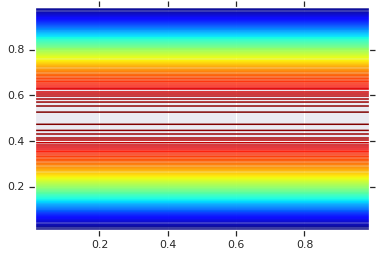
हालांकि, इस तरह के एक मॉडल से शक्ति, प्रायिकता इंटीग्रल ट्रांसफॉर्म का उपयोग कर रही है, मनमानी आरवी पर कोपुला का उपयोग करने के लिए, इस तरह, हम मनमाने ढंग से सीमांत निर्दिष्ट कर सकते हैं, और उन्हें एक साथ सिलाई करने के लिए कोपुला का उपयोग कर सकते हैं।

हम एक मॉडल से शुरू करते हैं:

\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]

और योजक का प्रयोग कर एक द्विचर आर.वी. पाने के लिए \(Z\), जो marginals है कुमारस्वामी और Gumbel ।

हम उन दो RVs द्वारा उत्पन्न उत्पाद वितरण की साजिश रचने से शुरू करेंगे।

a = 2.0
b = 2.0
gloc = 0.
gscale = 1.

x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)

# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)

pdf = x.prob(x_grid) * y.prob(y_grid)

# Plot its density

plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);

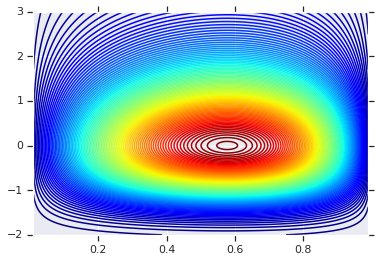
विभिन्न सीमांतों के साथ संयुक्त वितरण

अब हम वितरण को एक साथ जोड़ने के लिए गाऊसी कोप्युला का उपयोग करते हैं, और उसे प्लॉट करते हैं। फिर विकल्प के बारे में हमारी उपकरण है TransformedDistribution उचित आवेदन करने Bijector चुना marginals प्राप्त करने के लिए।

विशेष रूप से, हम एक का उपयोग Blockwise (जो अभी भी एक द्विभाजित परिवर्तन है) वेक्टर के विभिन्न भागों में अलग bijectors लागू होता है bijector।

अब हम अपने इच्छित कोप्यूला को परिभाषित कर सकते हैं। लक्ष्य सीमांतों की सूची (बीजेक्टर के रूप में एन्कोडेड) को देखते हुए, हम आसानी से एक नए वितरण का निर्माण कर सकते हैं जो कोपुला का उपयोग करता है और इसमें निर्दिष्ट सीमांत होते हैं।

class WarpedGaussianCopula(tfd.TransformedDistribution):
  """Application of a Gaussian Copula on a list of target marginals.

  This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
  which are distributed marginally (with CDF) [F_0, ... F_n],
  `GaussianCopula` represents an application of the Copula, such that the
  resulting multivariate distribution has the above specified marginals.

  The marginals are specified by `marginal_bijectors`: These are
  bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.

  block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
  length should be same as length of `marginal_bijectors`.
  See tfb.Blockwise for details
  """
  def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
    super(WarpedGaussianCopula, self).__init__(
        distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
        bijector=tfb.Blockwise(bijectors=marginal_bijectors,
                               block_sizes=block_sizes),
        validate_args=False,
        name="GaussianCopula")

अंत में, आइए वास्तव में इस गाऊसी कोपुला का उपयोग करें। हम की एक Cholesky इस्तेमाल करेंगे \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\), जो 1 प्रसरण के अनुरूप होगा, और सहसंबंध \(\rho\) मल्टीवेरिएट सामान्य के लिए।

हम कुछ मामलों को देखेंगे:

# Create our coordinates:
coordinates = np.concatenate(
    [x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)


def create_gaussian_copula(correlation):
  # Use Gaussian Copula to add dependence.
  return WarpedGaussianCopula(
      loc=[0.,  0.],
      scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
      # These encode the marginals we want. In this case we want X_0 has
      # Kumaraswamy marginal, and X_1 has Gumbel marginal.

      marginal_bijectors=[
          tfb.Invert(tfb.KumaraswamyCDF(a, b)),
          tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])


# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
  copula = create_gaussian_copula(correlation)
  copulas.append(copula)
  probs.append(copula.prob(coordinates))


# Plot it's density

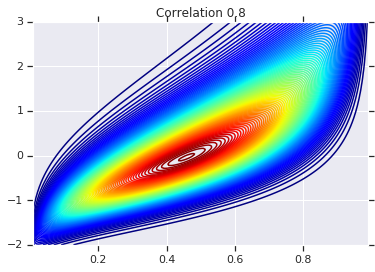
for correlation, copula_prob in zip(correlations, probs):
  plt.figure()
  plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
  plt.title('Correlation {}'.format(correlation))

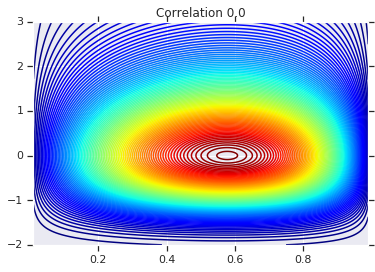
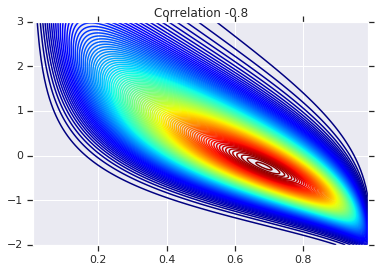
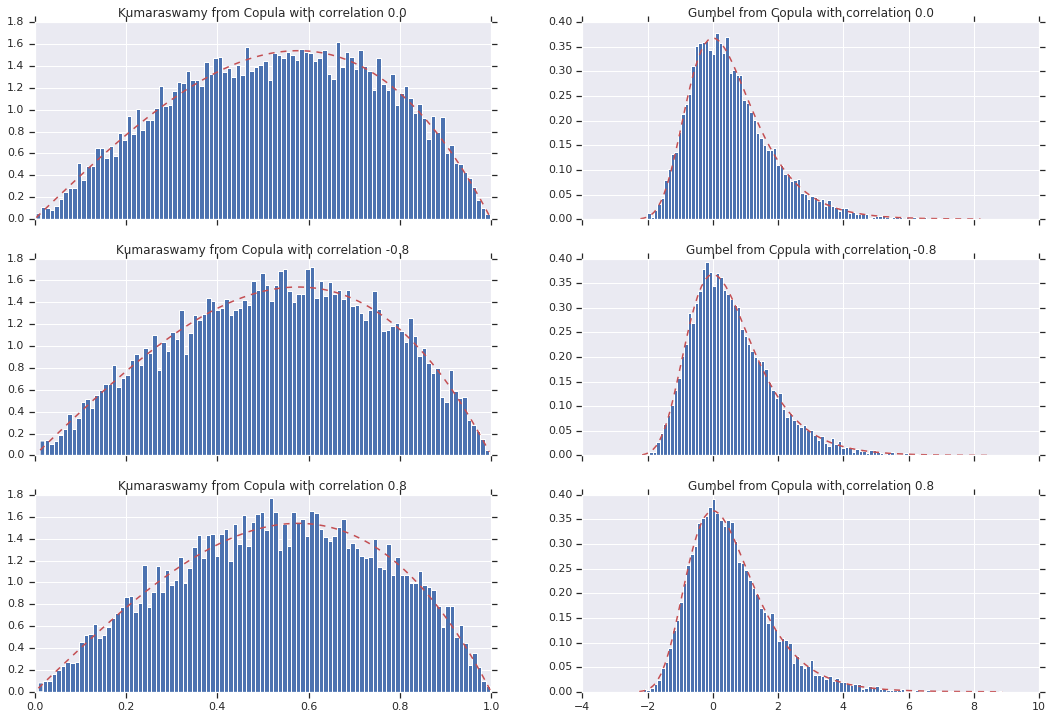
अंत में, आइए सत्यापित करें कि हमें वास्तव में वह सीमांत प्राप्त होता है जो हम चाहते हैं।

def kumaraswamy_pdf(x):
    return tfd.Kumaraswamy(a, b).prob(np.float32(x))

def gumbel_pdf(x):
    return tfd.Gumbel(gloc, gscale).prob(np.float32(x))


copula_samples = []
for copula in copulas:
  copula_samples.append(copula.sample(10000))

plot_rows = len(correlations)
plot_cols = 2  # for 2  densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))

# Let's marginalize out on each, and plot the samples.

for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
  k = copula_sample[..., 0].numpy()
  g = copula_sample[..., 1].numpy()


  _, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
  axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
  axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))

  _, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
  axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
  axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))

निष्कर्ष

और वहाँ हम जाते हैं! हम का प्रदर्शन किया है कि हम का उपयोग कर गाऊसी copulas निर्माण कर सकते हैं Bijector एपीआई।

आम तौर पर, का उपयोग कर bijectors लेखन Bijector एपीआई और उन्हें एक वितरण के साथ रचना, लचीला मॉडलिंग के लिए वितरण के अमीर परिवारों बना सकते हैं।